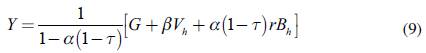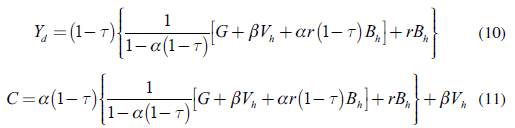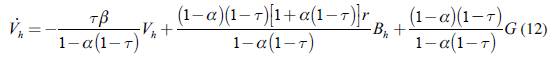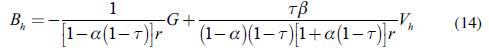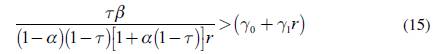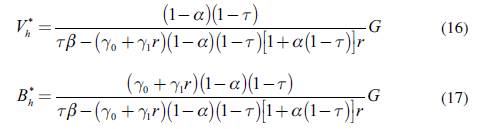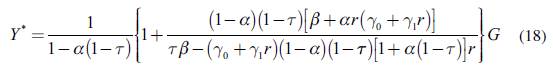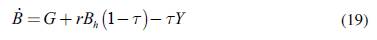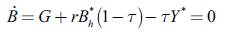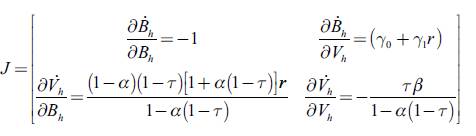INTRODUCTION

Some recent papers -including ^{Asensio (2017)}, ^{Bertocco and Kalajzic (2014)}, ^{Bertocco (2018)}, ^{Dafermos (2012)}, ^{Lavoie and Reissl (2018)}, and ^{Palley (2017)}-have revived the debate around the macroeconomic role of the Keynesian theory of liquidity preference in a world of endogenous money.

This theory, as developed in Chapter 15 of the General Theory and then popularized through the IS-LM model, played an essential role in the overall Keynesian edifice. As well as representing an alternative to the loanable funds story, it constituted a theory to determine both the interest rate and the level of economic activity.

As is well known, the theory of liquidity preference was developed under the framework of exogenous money or, as ^{Dow (1997)} would probably put it, money exogenous to the private sector and endogenous to the banking system. Money, however, is certainly endogenous. This is now unanimously recognised and has been incorporated as a key ingredient in the so-called New Consensus in macroeconomics. This is a fact of life that is recognised even by the many (the large majority of the profession) who still adhere to the Wicksellian loanable funds theory and believe in the existence of a natural interest rate determined by the fundamentals of thrift and productivity. ^{Carlin and Soskice (2015)}, who made a great effort to spread and clarify the neo-Keynesian perspective by means of very elegant and accessible models, are very explicit: "When the central bank sets the policy rate, it allows the supply of money to adjust to whatever is the level of demand" (pp. 158-159).

Does this "fact of life" imply that the Keynesian theory of liquidity preference becomes a useless tool? In the New Consensus -at least in its "teachable" versions- the answer seems to be positive. Again, according to ^{Carlin and Sos-kice (2015)}: "...structural changes in the economy that shift the private sector's demand for money do not alter the central bank's ability to achieve its desired output gap.any shift in the money demand function affects the money supply [endogenous money] but does not feed back to influence real economic activity" (pp. 158-159; authors' italics).

In a very useful representation of the New Consensus 3-equation model, ^{Lavoie (2009)} shows things are a bit more complicated. A rise in liquidity preference, which is represented as a "Minsky moment" (a rush towards liquidity and risk-less assets that prompts an increase in market rates relevant to the private sector's spending decisions), does have a temporary recessionary impact. However, if the central bank is able to revise downward its estimate of the natural interest rate and reduces the policy rate accordingly (which is not to be taken for granted since market rates are on the rise), then the economy will return at its NAIRU equilibrium, and inflation will be on target. A variation in liquidity preference, despite its real, short-term effects, does not modify the steady-state position of the economy.¹

Post-Keynesian authors do not have a unique position in this respect. Roughly speaking, we can say that some authors, the so-called "early horizontalists"² (for instance ^{Moore, 1988}), believe in the banking system's ability of to fix the interest rate at its chosen level and then follow ^{Kaldor (1985)} in denying any significant role to liquidity preference:³

"... 'liquidity preference' was regarded as the essential factor that distinguished Keynesian from pre-Keynesian theories.... All this, however, depended on the assumption of the quantity of money being determined irrespective of all other factors that determined the demand for goods and services. If we regard money as an endogenous factor, liquidity preference and the assumption of interest-elasticity of the demand for money cease to be of any importance" (p. 9).

Quite an astonishing parabola: from being the cornerstone ("the essential factor") of the Keynesian edifice, liquidity preference "ceases to be of any importance".

Other authors, the so-called "structuralists" (^{Dow, 1997}; ^{Palley, 1994}, ²⁰¹³, ²⁰¹⁷), believe that the banking system behaviour is characterized by a traditional upward sloping loans' supply curve - the interest rate goes up with credit expansion and constitutes an endogenous variable of the system. In this case, money is endogenous, but the liquidity preference of the public may matter again. As was the case in the General Theory, it might constitute a key parameter when determining both the interest rate and the level of economic activity:⁴ "An increase in liquidity preference puts upward pressure on interest rates, which, in turn, puts downward pressure on output and employment, as long as the money supply is constrained to some degree" (^{Dow, 1997}, p. 64)

This debate is very important not only for its analytical and theoretical implications, but also for political reasons. It is essentially a debate around the relative roles of and distribution of power between banks (the banking system) and financial markets - horizontalists (and their Modern Monetary Theory followers) who give prominence to the banking system. These structuralists recognise a crucial macroeconomic role for financial markets, "money managers", and other similar factors. In a sense, the Keynesian theory of liquidity preference was a recognition of the power of the City and how its changing mood and orientations could seriously affect the real economy and the concrete prospects of firms and households.

In this paper, we will try to contribute to this debate from a different and in many respects much simpler perspective. Our purpose is to show that liquidity preference does not have to affect the interest rate in order to affect the real economy: this is the central message of the paper and, needless to say, the implication is that the quarrel between "structuralists" and "horizontalists" is, in a sense, not so central. We will argue that a sufficient (yet, not necessary) condition to give liquidity preference such a relevant role in the determination of the steady-state level (or growth) of output is that banks' profits are not fully distributed to households. Or, if they are and the model includes different categories of households instead of pooling them together, those households receiving banks' profits have a different propensity to spend from other households. Section 2 illustrates the basic idea of the paper, and section 3 provides a specific example by developing a simple formal model. Section 4 concludes.

THE BASIC IDEA

Think of a closed and private economy. There is no government and, according to the principle of effective demand, aggregate demand (C + I) determines the level of output Y. There are two modalities for firms to finance their investment spending. Either they get loans from the banking system or they issue some kind of securities (for the sake of the argument, we assume retained profits away). Securities are subscribed by households, whereas the banking system makes "traditional" loans to firms. The portfolio choice households make is one between holding their wealth in the form of money (bank deposits)⁵ and/or in the form of securities. Provided that firms are indifferent to either raising funds one way or another, a simple arbitrage argument imposes that the interest rates paid on securities and on bank loans must be the same. Hence, we will refer to "the" interest rate in this economy. It could also postulate that, for given expectations, firms' investment spending is negatively affected by the interest rate. In terms of aggregate consumption, it is reasonable to assume this is positively affected by households' current income and the level of their accumulated wealth. Money is endogenous. Under the present framework, this means that each time some credit demand is judged to be creditworthy, the banking system creates money (deposits) ex-nihilo, and loans are extended at an interest rate established by banks themselves. Banks do not pay interest on deposits, and their profits (i.e. interests received on loans) are entirely distributed to their owners (households).

Let us suppose that this economy is in some steady-state position, with output and households' incomes growing at some steady rate (eventually zero), and the interest rate is constant at the level decided by banks. At a point, for some reason (uncertainty, a sunspot, whatever), households increase their liquidity preference. They do not want to subscribe securities at the same rhythm as before and, ceteris paribus, the supply of credit decreases. This, for some given credit demand (some given firms' investment plans), would push the interest rate up. The banking system, however, does not want the interest rate to deviate from the target and, as such, steps in and increases its own supply of loans to firms. At an unchanged interest rate, investment demand will remain the same as before, but, due to the change in liquidity preference, more investments will be funded out of bank loans and less out of securities. The increase in liquidity preference would, therefore, not affect the number of investments.

What about aggregate consumption? Despite the change in its composition, the level of households' wealth is unchanged: a slightly less securities and slightly more of money. In terms of their income, households are receiving less of interest payments through securities, but are receiving more profits from banks. Therefore, neither their wealth nor their income are affected and, thus, aggregate consumption will remain the same. With unchanged aggregate demand, output (or output dynamics) cannot change either: liquidity preference is then completely irrelevant, it "ceases to be of any importance". In a world of endogenous money, neither the interest rate nor output change in response to its variations. Kaldor was right.

This conclusion clearly rests on some very questionable assumptions: three of which seem be particularly relevant. First, in the development of the previous argument, capital gains (losses) on the holding of bonds were implicitly assumed away. Taking them into consideration would force us to recognise that households' wealth and its evolution over time (and then aggregate consumption followed by output) do not depend exclusively on households' overall savings, but also on how these savings are allocated between money and bonds since the latter is the only item on which capital gains (losses) may mature. In other words, should capital gains be taken into account, liquidity preference, i.e. the way of allocating savings, would become a crucial determinant of aggregate demand.

A second assumption the removal of which would compromise the validity of the Kaldorian view is the idea that securities and bank loans are perfect substitutes. Most probably, in the real world they are not, for both microeconomic and macroe-conomic reasons. At the micro level, one should recognise that from a firm's (the borrower) perspective, getting money through bank loans is not the same as getting money by issuing bonds. Bank loans are invariably associated with the so-called "covenants", i.e. the conditions that are imposed on the borrower to do certain things, whereas bonds give the borrower much more freedom. On the other hand, bank loans are certainly more flexible than bonds since it is always possible to renegotiate important conditions with the bank, including the rollover of the debt. At the macro level, it is important to see that in any concrete economy there are small and large firms and issuing bonds is simply not an option for small ones. Under these circumstances, if liquidity preference goes up and it becomes more difficult (costly) for large firms to become financed by issuing bonds, banks should reduce interest rates to guarantee the same level of investments. In any case, they will want to keep the interest rate constant and investments will then be likely to fall. In any case, liquidity preference would no longer be neutral.

A third very important assumption without which the discourse on the irrelevance of liquidity preference would lose its own relevance is that banks' profits are fully distributed to households. In this case, and only in this case, when liquidity preference increases and a higher portion of total investments is funded by bank loans, households' current income is unaffected: households receive less interest income from holding bonds but more of banks' profits. Again, real-world banks' profits are never fully distributed. A positive fraction of these profits are retained for compelling reasons. It is not only (and not mainly) the fact that in most countries banks must have their own funds to comply with regulations that stipulate a minimum capital adequacy ratio. To have a deeper level of understanding, it should be remarked that banks themselves, regardless of any external imposition, want to accumulate their own funds to continue having their liabilities accepted as means of payment. To be as concrete as possible: no one would try to get a loan from a bank whose liabilities are not generally accepted as a means of payment: liabilities are accepted as a means of payment in that they are backed by bank's own funds. To state this in a different way: it is certainly true that money is endogenous, and private agents (banks) create money just by issuing liabilities. However, this is only possible to the extent that those liabilities are somewhat backed by a safe source of funds: banks' own funds and/or reserves held at the central bank. These are the very strong reasons why banks' profits are never fully distributed; however, there are more reasons. Until now, we have generically referred to "banks" or "the banking system" without discriminating between "ordinary" banks and a central bank. The very existence of a central bank is a further and very good reason to admit that profits of the "banking system" are never fully distributed to households. Indeed, central banks' profits are traditionally distributed to governments, not to households.

In principle, it would be possible to build a model for each of the cases we briefly illustrated: a model with capital gains/losses, a model where bonds and bank loans are not perfect substitutes, and a model where banks' profits are not fully distributed. It could be shown that, in any of these cases, liquidity preference matters: the interest rate is fixed, somewhat decided by the banking system, yet variations in liquidity preference affect the steady-state path of the real economy. A similar argument may be developed for an economy with a government issuing bills and bonds and a central bank that fixes the interest rate and, thus, at this rate buys whatever quantity of government securities the market is not willing to subscribe. Of all these possible institutional settings, this is the exact framework we are going to use. We will show what happens when there is a central bank and its profits are distributed to the government. We will see that in this admittedly very general case, postulating a system of pure endogenous money when the interest rate is exogenously decided by the central bank, does not prevent liquidity preference from playing a crucial role in determining the system's real equilibrium.

THE MODEL

A number of simplifying assumptions are made for the model. The economy is closed and produces one commodity (GDP) which may be used either for private or governmental consumption. There are no investments, i.e. the economy is a pure labour economy (^{Pasinetti, 1981}). Households pay taxes on their gross disposable income. As well as relying on fiscal revenue, the government may finance its expenditures by issuing bills. Both households (as a part of their portfolio choice) and the central bank (as part of its monetary policy) subscribe these bills. The latter prints high-powered money (H) to buy governmental bills. The central bank's profits (interests on government bills) are assumed to be distributed back to the government (a very common practice in the real world). There are no commercial banks and, therefore, no bank money. Households hold their savings either in cash (under the pillow or in a safe at home) or in government bills. There is one price for bills and this stays constant (as argued above, we abstract from capital gains). Commodity prices are also fixed since including inflation into the model would not affect our argument.⁶ Finally, the economy is fully demand-driven, and firms produce whatever is in demand (the inclusion of some kind of supply constraint would not add or take anything away from our argument).

The above assumptions translate into an extremely simplified model: de facto a slight modification of a model originally proposed by ^{Godley and Lavoie (2007)} whose purpose was not to discuss the role of liquidity preference. To make it even easier, the model is written in continuous time (as usual, a dot over a variable indicates its time derivative, i.e. )

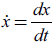Equation (1) is the fundamental identity of national accounts. In our Keynesian framework, it also illustrates the principle of effective demand. Equation (2) is a definition of households' disposable income: on top of factors' income (here, labour income only), households receive interest payments on their accumulated stock of government bills (B_h) and pay taxes. Equation (3) specifies the tax base (households' total income) and the tax rate (t). It is worth noting that in the kind of model we are developing taxes must be included, otherwise the economy would never reach a meaningful steady-state. Indeed, this is a model where investments and technical improvements are ruled out and therefore there is no positive steady-state growth. Under such circumstances, with no taxes, the government debt-to-gdp ratio would go on to infinity. In other words, if we want a steady-state with G > 0, in such a steady-state the government budget must be balanced (T = G), and we will see that, under reasonable assumptions, this is exactly what happens in this economy.

Equation (4) postulates aggregate consumption to depend on both current disposable income and accumulated wealth (V_h), and the relevant propensities to consume are, a and β, respectively. Accumulated wealth, in turn, evolves as indicated by equation (5): it goes up (down) whenever aggregate savings are positive (negative). Equation (6) is the most important in the model since it incorporates the idea of liquidity preference. This equation says that households' demand for bills is the difference between the amount (or value: in this model there is no difference) of bills households would like to hold and the amount they actually hold (the two must coincide in a steady-state). The former is just a fraction of total wealth, and such a fraction depends positively on the interest rate on bills (y ₁ > 0) and on the exogenous parameter y₀. This parameter is an indicator of the state of liquidity preference: the lower y₀ the stronger the preference for liquidity of the public. Of course, overall consistency requires 0 ≤ γ ₀ + γ ₁ r ≤ 1. Equation (7) simply states that what remains of people's wealth goes to cash. Equation (8) fixes the interest rate at the level desired by the central bank.

The model is squared -there are eight independent equations with eight unknowns ( 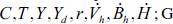is taken as given, whereas V_h and B_h are state variables, i.e. given at any specific instant in time)- and it could be noted that we neither have an equilibrium condition for the bills' market nor one for the money market. This because of Walras' law and especially because we are assuming, for the sake of the argument, that money is endogenous. Imagine the government wants to sell a given quantity of bills to spend more, but households are not willing to subscribe the totality of them. Should the central bank decide not to intervene, the government would be left with other options: either to spend less than originally planned, to increase the interest rate on bills to convince people to buy them, or some combination of the two. We suppose the central bank buys whatever amount of bills are not subscribed by the market so that the government does not have to raise interest rates. This is the concrete way for the central bank of this model economy to control the interest rate and, at the same time, the reason why we do not have to include an equilibrium condition for the bills market in our model. This is also the reason why we do not need a money market equilibrium condition: should people decide to hold more money (to sell some of the bills in their hands), the central bank would simply provide that cash and buy those bills. As such, the interest rate would remain at the level decided by the central bank itself.

The model is simple, and finding its solution is easy. The following comes from the first four equations (forming an autonomous sub-system yielding the solutions for Y, C, Y_d, and T):

This is the standard formula for the Keynesian multiplier: in the short-run, equilibrium GDP is a multiple of autonomous demand, which, of course, includes the interest payments received by households on the stock of bills held at the beginning of the period.

Equation (9) represents a short-term (or temporary) solution. Moving towards the steady-state solution of the model means studying the evolution over time of both V_h and B_h (taken as given in (9)). This is where (5) and (6) enter into the picture. Before analysing the steady-state solution of the model, however, note that liquidity preference (the parameter y₀) does not play any role in determining the short-term equilibrium GDP since the interest rate is taken as a given and decided upon by the central bank (in a more complete model, by the banking system). One could then be tempted to agree with the severe Kaldorian claim that liquidity preference "ceases to be of any importance" since, in a framework of endogenous money, it neither affects GDP nor does it affect the interest rate. To see what is different, we should move to the steady-state solution of the model.

Using (9), (2), (3), and (4), we get to the short-term equilibrium values for disposable income and aggregate consumption:

At this point, using (5), straightforward algebraic manipulations make it possible to have a differential equation for the evolution over time of households' wealth:

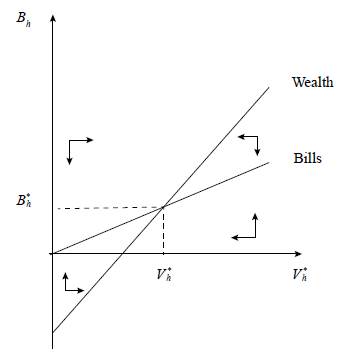
Not surprisingly, (12) makes the evolution of households' wealth depend on its initial value (V_h), the initial value of the stock of bills held by households themselves (B_h), and the level of public spending (G, which is the ultimate source of autonomous demand in a closed economy and then, in a Keynesian framework, the true origin of income, savings and wealth). We are now left with the dynamics of the stock of bills in the hands of households. Luckily though, we no longer have to make calculations since these dynamics are already described by (6). The reader may easily see that (6) and (12) form a linear system of two differential equations in the two unknowns V_h and B_h. A steady-state for this economy is one in which V _h = 0 and B _h = 0. All we have to do is to show such a steady-state exists and is stable. As usual, the simplest way to address this kind of issue is to draw the phase diagram and see how the stationary loci for the relevant state variables behave. The stationary locus for B_h, i.e. the set of infinite pairs (V_h, B_h) such that B _h = 0, is

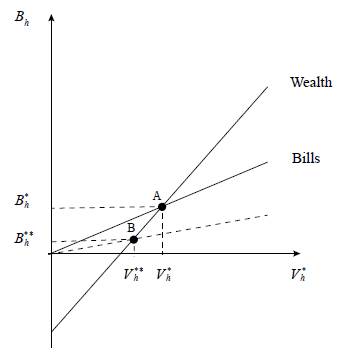
The slope of this isocline, labelled as "Bills" in Figure 1, is positive and less than one, as we already saw. The equation of the isocline V _h = 0 - labelled as "Wealth" in Figure 1 - is:

The two isoclines have been drawn under the assumption that the slope of the "Wealth" schedule exceeds the slope of the "Bills" schedule, which is a condition for a meaningful steady-state to exist:⁷

Assuming (15) holds, the steady-state solutions are easily computed:

The solutions (16) and (17) are then to be inserted into (9) to get the steady-state level of GDP. In the steady-state, in this closed economy, the sole source of autonomous demand is public spending, so it is not surprising to see that the steady-state level of GDP increases with G in this model economy:

In our model economy, there are no supply constraints (a better situation would be: a "pure labour economy", labour is always available upon demand).⁸ Also, the system is demand-driven and public spending in a closed economy is the unique component of autonomous demand. This is the origin of the result illustrated in (18): in the model economy, you cannot have a positive steady-state income if you do not have a positive level of public spending. The question, then, naturally arises: what about government deficit and debt? It is very easy to check that in the steady-state the government budget is balanced. One way to do so is just to write down the differential equation for the evolution of public debt (we will call "B" the total stock of public debt). Remembering that central bank's profits are paid back to the government (which means that de facto interests are only due on the portion of debt in the hands of households, B_h), the relevant equation is:

According to (19), the government has to issue bills to finance the excess expenditures (over the fiscal revenue). Using (17) and (18), the reader may check that in the steady-state

In other words, in the steady-state, the government debt remains constant, i.e. its deficit is zero. In this closed economy with no capital, investments, and growth, the steady-state must be one where households do not save and the government does not issue new debt.

It could be worth noting that, in this model, an increase in the interest rate is expansionary. Using (16), (17), and (18), it is easy to see that households' wealth, their holdings of bills, and GDP increase together with the interest rate. This could sound strange; however, in the present framework, it is not. Indeed, when the interest rate increases, households receive a higher interest income on their existing holdings of bills and, on top of this, their portfolio choice shifts from money to bills. An increase in households' income, in turn, translates into higher consumption, aggregate demand, and GDP. In the transition to the new steady-state, a higher household income stimulates their savings; then it is not surprising to see that in the new steady-state their wealth has also increased. It would be easy to weaken this "strange" result, at least in two ways. One is to add investments to the model and assume they negatively depend on the interest rate. The other is to postulate some direct and negative relation between consumption and the interest rate,⁹ and this could be justified on the grounds of some standard neoclassical argument -with higher interest rates, people postpone consumption (substitute present with future consumption) to maximize their inter-temporal utility. However, this would not change the main insights of our discourse on liquidity preference and, therefore, we will not pursue this route.

Turning to more interesting questions, we still have to analyse whether the steady-state we arrived at is stable or not and, above all, understand the role of liquidity preference. The stability of the system is to be evaluated looking at the trace and determinant of the Jacobian (J) of the linear system formed by our dynamic equations (6) and (12), i.e.

The trace of J is certainly negative and, provided that (15) holds, the determinant is positive. In other words: if a steady-state exists (remember that (15) is an existence condition), it is stable (as indicated by the arrows in Figure 1).¹⁰ We can then move to the issue of liquidity preference.

Assume the economy is in its steady-state position (point A in Figure 2). For some reason, the preference for liquidity of the public increases (y₀ falls). People try to sell their bills and, as we already know, the central bank will buy them and print money. The interest rate will remain unaffected (in this model, this is the ultimate purpose of the central bank) and money supply will adjust endogenously.

The "Bills" schedule will rotate clockwise (see equation (13)) and the economy will move towards its new steady-state (point B in Figure 2), with V ^** _h < V _h ^* and B _h ^** < B _h ^* . As the reader may easily check using (18),¹¹ the steady-state level of GDP will also decrease: in a world of endogenous money, liquidity preference continues to be of great importance in the determination of real GDP. This cannot be considered a theory anymore to determine the interest rate (at least under the simplifying assumptions of this model), but it continues to be a crucial parameter in the determination of income. The reason is simple, and was already mentioned in section 2. The choice of households to increase their holdings of money (decrease their holdings of bills) does not leave their incomes unaffected. This choice reduces their incomes (then consumption, aggregate demand, and GDP) simply because bills are interest-bearing, money is not, and the extra-profits earned by the central bank are not (fully) distributed to households.

So, a naïf question could be asked by someone with a neoclassical background: why should households hold money in the first place if this does not maximize their income and welfare? Are they irrational? Of course not, and the answer to this question is well-known, and provided by Keynes himself: when people feel unsecure, they buy insurance services, and these are not free. They are costly. The kind of uncertainty Keynes dealt with is the so-called "radical uncertainty" and the only (costly) insurance service that might be bought in this case is given by the use of money as a store of value. There is nothing irrational.

A further naïf question one could be tempted to ask regards inflation. If we compare the two steady-states illustrated in Figure 2, we clearly see that, after the increase in liquidity preference, the economy ends up with a lower GDP and an increased quantity of money. How is it possible for this higher quantity of money not to translate into higher commodity prices (remember that in our model we assumed prices to be constant)? Once again, the answer is very simple. Consider the Fisher identity. The kind of shock we are talking about -a stronger liquidity preference- is very much the same as a reduction in money velocity. What we showed, then, is that the macro causality embedded in a Keynesian model with endogenous money simply implies that a reduction in money velocity is offset in part by a reduction in real GDP and in part by an increase in the quantity of money: the Fisher identity, as it must be, holds before and after the occurrence of the shock. In the concluding section of the paper, we will briefly discuss some possible extension of this model and this includes the inclusion of some price dynamics. In terms of the Fisher identity, instead of having only M and Y as endogenous (as is the case in our model), we would also have P as emerging endogenously from the system. Money velocity, V, would instead continue to be the crucial exogenous variable.

FINAL REMARKS

In this paper, we have argued that even in the event that banks are able to maintain the interest rate at their chosen level- which is, so to speak, the most "radical" version of the theory of endogenous money- the general public's liquidity preference (known as "financial markets") continues to be a key element in determining the real equilibrium of the economy. Under an endogenous money framework (at least in its radical and "horizontalist" version), the Keynesian theory of liquidity preference does not constitute a theory that can determine both the interest rate and the level of income. However, it does not lose its great importance as theory to be able to determine income. Financial markets matter, even when assuming that banks do have the full power to control the interest rate. The Kaldorian idea that, with endogenous money, liquidity preference "ceases to be of any importance" can only be defended under a set of very restrictive assumptions (banks' profits are fully distributed and there is no difference in the propensity to spend for those households who receive banks' profits and those who do not; capital gains and losses are not taken into consideration; bank loans and bonds are perfect substitutes from the perspective of borrowing firms).

The very simple model we used as an example to illustrate the essence of our idea may obviously be extended in several directions. One possibility is to include investments and turn the model into a Keynesian growth model. In this case, instead of only having savings out of the steady-state (as is the case in the model we presented in this paper), we would also have savings in the steady-state. With private investments brought into the picture, it would make sense to postulate the existence of private banks and then bank money (deposits). High-powered money would cease to be the only form of money and the model would certainly be descriptively richer. In any case, with or without private banks and bank money, a crucial issue which is not addressed in this paper regards the reasons why banks -central and/or private- decide the specific interest rate (as we saw and discussed in (16), (17), and (18). The interest rate is not neutral and its specific level affects the steady-state position of the economy): this is, in our opinion, the potentially most fruitful extension of our model. Adding to the model, some kind of monetary rule -the Taylor rule or some other relation describing banks' objectives- would make it possible to address other interesting issues related to the role of liquidity preference.

For instance, it would be possible to study how variations in liquidity preference (which, as we saw, modify output and employment and then, through some kind of Phillips curve, inflation) force the central bank to change the interest rate. This way, the central bank would probably manage to restore the target level of inflation, but what about output and employment? If the central bank is not pursuing an inflation targeting policy and, as is the case in the US, this is more oriented toward guaranteeing full employment, what would the consequences of variations in liquidity preference be on the equilibrium inflation rate? In other words: is it possible for the central bank to control both the inflation rate and the output (or output gap) in a framework where liquidity preference is once again important? The inclusion of a central bank with some well-specified objective in our model would also allow understanding why there are instances where monetary policy is not very effective. In our model economy, for instance, the central bank could decide to increase the interest rate to stimulate the economy (see discussion above), but it is perfectly possible for this not to work if, at the same time, people increase their liquidity preference (if, in the model, r goes up and y₀ falls).

In a different model where the impact of higher interest rates on aggregate demand is negative (see, again, our previous discussion), the very same risk could materialize: the central bank lowers the interest rate to boost activity, but this does not work because people increase their liquidity preference. So, regardless of the specific model, we work with interest rates that positively affect or negatively aggregate demand, with or without investments, etc.). The central message of our paper is that liquidity preference matters. The fact that money is endogenous does not necessarily move the balance of powers in favour of banks. The City and Wall Street continue to affect our lives.