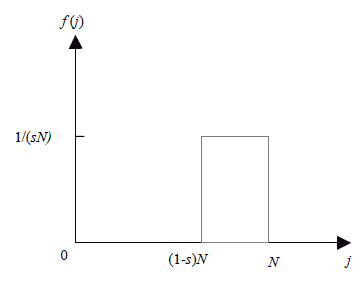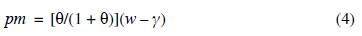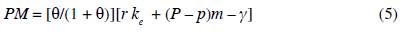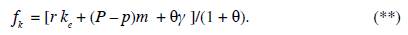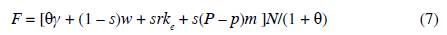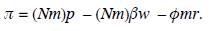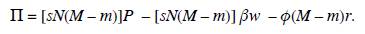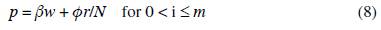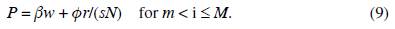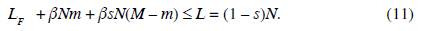INTRODUCTION
A long tradition of development economics that originates from Adam Smith (1776) has sustained the importance of both "division of labour" and "extent of the market" as fundamental engines of economic growth. These engines would today be called productive diversification and effective demand. According to Smith, their interaction brings about the circular causation of income: the sequence of productive diversification (technological change), exploitation of scale economies, and expansion of the population's purchasing power that increases products and income so that this economic cycle continues to operate at an ever higher level. Hence, productive diversification and effective demand push the process of economic growth in a spiral shaped virtuous circle that goes from supply to demand and vice versa.
Some links must be explained in order to understand why "extent of the market" could be used in modern jargon meaning effective demand. First of all, the literal meaning of "extent of the market" in the Wealth of Nations (Smith, 1776) is market size:
"As it is the power of exchanging that gives occasion to the division of labour, so the extent of this division must always be limited by the extent of that power, or, in other words, by the extent of the market. When the market is very small, no person can have any encouragement to dedicate himself entirely to one employment (...). There are some sorts of industry, even of the lowest kind, which can be carried out on nowhere but in a great town" (Smith, 1776, I, III [1981, I, p. 31]).
It could also be said that Smith refers to the population's purchasing power ("power of exchanging"). Notwithstanding, when he claims that some industries require a large-scale demand, like that of a big town, he is also contemplating how purchasing power becomes actual demand, which is nothing other than the concept of effective demand.
Although Smith describes the supply effect (technological change and productive diversification) as the spark that ignites the growth process, he does not neglect the necessary supporting role of effective demand. In his view, both supply and demand concur in a related but relatively independent way to the economic growth process. Thus, a limited market size or a high concentration of income might slow down economic activity and even stop it. In fact, according to Smith, the economic process cannot unfold if the expansion of supply, which is driven by a higher productivity, is not matched by an increased effective demand that can only come from economic activities where the distribution of remunerations to productive factors is sufficiently homogeneous. It is in this sense Smith claims that the extent of the market limits the division of labour. Based on Murphy, Shleifer, and Vishny (1989b), this paper explores some microeconomic foundations for Smith's claims about the importance of effective demand for the economic activity level.
After the triumph of the neoclassical school, when it became mainstream, most economic analysts ended up believing one way or another that demand follows from supply, as proposed by Say's law (Say, 1803). The criticism by many economic thinkers of this so-called law (Currie, 1981; Keynes, 1936; Malthus, 1820; Marx, 1867; 1885; 1894; Murphy, Shleifer, & Vishny, 1989a; 1989b; Nurkse, 1953; Rosenstein-Rodan, 1943; Young, 1928) has been ignored or at least neglected. In fairness, it has to be said that the Post Keynesian economic school has consistently sustained that effective demand impacts economic growth (Domar, 1946; Dutt, 2003; Harrod, 1939). Notwithstanding, probably due to Keynes' huge impact on short-term macroeconomic analysis, the role of effective demand is usually thought of as a short-term economic activity level issue. For the long-term, the conventional wisdom is that demand follows supply, and that is it. This is not surprising if one takes into account that most neoclassical models of economic growth ignore the impact of effective demand on long-term growth. These models usually consider consumers as if they were endowed with homothetic and non-satiable preferences. Under this assumption, income distribution becomes irrelevant because the expenditure distribution is fixed regardless of the consumer's income level (Murphy et al., 1989b). Moreover, to take the issue to an absurd level, just one single consumer with these preferences and enough income could replace the consumption of millions. Thus, economic models with homothetic and non-satiable preferences obey Say's law if it is assumed that factors and goods are mobile, prices are flexible, transaction costs are negligible, and markets clear.
Following the Smithian vision of economic development, Murphy et al. (1989a & 1989b) emphasized the impact of industrialization and population purchasing power on economic growth. The second paper in particular builds a model where the market size and the distribution of income play a central role in the explanation of economic activity. However, due to the difficulty of the subject, the authors focused their analysis on the proof of the existence of economic equilibrium in a general setting that embodies the complex interaction among workers, capitalists, and landowners with different configurations of wealth and income distribution. The added value of this paper is, then, to build a simpler mathematically tractable model in which the interaction between capitalists and workers highlights the role of capital distribution (and income distribution) as a fundamental feature of the aggregate level of economic activity. In order to do so, preferences are assumed to be non-homothetic (there is a minimum level of food consumption per capita), and consumption of manufactured goods is supposed to be satiable (either none or just one unit of each manufactured good is consumed per person). Labour distribution and capital distribution are assumed to be homogeneous: the simplest possible distributions of wealth and income. The model reveals that an excessive concentration of wealth and income can cause the price system to fail. The model, as will be explained below, is not free of mathematical complexity. Nonetheless, numerical results are attainable through the use of electronic spreadsheets.
The important feature of product diversification as a mechanism to enhance productivity is not included in this model in order to keep the economic system as simple as possible. Hence, the paper is unable to address the important issue of economic growth. Instead, the effect of wealth distribution on the economic activity level is emphasized. Besides, the productive effect of product diversification has been extensively analysed in well-known models of economic growth.
The Model
Consider a market economy where only food and manufactured goods are produced. Food technology is given by the following Leontief production function: F/α= min(KF, L F ), where F is the food production in the period of analysis, a is a given level of multifactor productivity in food production, and K F and L F are the amounts of capital and labour used in this activity. The cost function associated with this technology under competitive conditions is given by C(F) = [(r + w)/α]F, where r is the user cost of capital, and w is the wage. Given the linearity of the cost function, the profit function of the food sector is also linear in F: Π F = [1 - (r + w)/α]F. Notice that food is taken as numeraire. In a competitive environment with flexible prices and free mobility of productive factors, profits are reduced to zero. Hence, the factor price frontier is given by:
The Leontief technology embodies perfect complementarity between the factors. A more general technological specification, such as a CES production function, would model factor substitutability at the cost of greater mathematical entanglement since non-linearities would be introduced at the beginning. In any case, the factor price frontier yields, as always, an opposing relationship between capitalists and workers at the distribution level.1
Given food technology, the factor demands in the agricultural sector are defined by:
Capital and population, K and N, are given at any production period. Labour is homogeneously distributed among the N members of this economy (one unit per capita). For mathematical simplicity of the model, it is assumed that property of capital is homogeneously distributed among capitalists, who represent a fraction s of the society. Capital property concentration is thought of as the inherited result of a historic process of capital accumulation. It is also assumed that no one can be a worker and a capitalist at the same time; these roles are exclusive. Hence, at any production period there exist sN capitalists and L = (1 - s)N workers. Figure 1 depicts the distribution function of capital property for N members of the society ordered by j according to their capital rents (first workers and then capitalists).
Labour and capital are assumed to be inelastically supplied at non-negative remunerations.
Let us now consider the typical worker consumption problem. Preferences are given by the following utility function: Z(f w , m) = ln(f w - y) + θln(m), where f w is the amount of food consumed in the period of analysis by the typical worker (and all workers are alike), y is the minimum amount of food that a person needs during the production period, m is the diversification index of manufactured goods for workers, and 0 is a positive number that measures the consumer's bias towards manufacturing consumption.2 The marginal utility of food decreases with its own consumption. Only one or none of each manufactured good is consumed; and the marginal utility of manufactured goods decreases steadily with their own diversification, m. The typical worker budget restriction is given by the following expression: f w + pm = w, where p is the price of the manufactured goods consumed by workers. As shown below, the demand and technology of all manufactured goods demanded by workers are the same across goods. Hence, they have a single common price. Utility maximization subject to the budget restriction yields the following demand functions:
And
Hence, the typical worker consumes manufactured goods if and only if the wage covers at least the minimum food demand (m ≥ 0 if and only if w ≥ y).
Capitalists consume all the manufactured goods which are demanded by workers, m, plus some others, M - m. The manufactures of general use, those indexed between 0 and m, will, from now on, be called the high-demand goods. Thus, for a typical capitalist, the consumption problem is set as follows: maximize Z(f k , M) = lnf - y) + θln(M) subject to the following budget restriction: f + pm + P(M - m) = rke, where f is the amount of food consumed in the period of analysis by the typical capitalist (and all capitalists are alike), M is the typical capitalist index of manufacturing consumption diversification, P is the common price of all those manufactured goods which are only demanded by capitalists, they will be called the low-demand goods, the difference M - m is the range of low-demand manufactured goods, and k e is the amount of effective capital per capitalist (as is shown below, capital might be unemployed, hence ke ≤ k ≡ K/(sN). This distinction between capital supply and capital demand is key to solving the model. The typical capitalist budget restriction means that he/she consumes food and high-demand manufactured goods as any typical worker does as well as some other manufactured goods. As in the case of high-demand goods, supply and demand of low-demand goods are assumed to be identical across these goods; that is why they all have the same price. The solution to this optimization problem yields the following demand functions:
And
Notice that a sensible general equilibrium for a market economy must imply that the typical capitalist remuneration, rke, is higher than the wage, w. Otherwise every capitalist would prefer to become a worker, and the capitalist society would implode.
Effective aggregate capital demand is given by
where K e is the fraction of total capital, which is effectively used in economic activities. In a market economy, this would imply that capital shares yield a lower return because some capital fraction, K - Ke, might be unemployed.
Food demand has two components: workers' demand and capitalists' demand. Thus, aggregate food demand is given by F = (1 - s)Nf w + sNf k . In the previous expression, by substituting the demand for food from a typical worker, f w (equation (*)), and the demand for food from a typical capitalist, f k (equation (**)), yields the aggregate food demand:
Manufactured goods are all produced with the following technology: a fixed investment of Φ units of capital is needed in order to create a new manufactured good. Besides, β units of labour are required to produce one manufactured good. This cost structure implies a technology with increasing returns to scale.
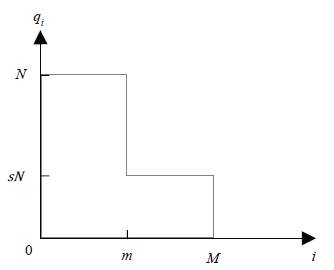
Taking into account that each person in this economy consumes one or none of each manufactured good, the demand structure for the whole range of manufactured goods is shown in Figure 2.
In this figure, qi represents the society's consumption of the i-th manufactured good. Every individual consumes one unit of all high-demand goods (0 < i ≤ m); and every capitalist consumes one unit of all low-demand goods (m < i ≤ M). The total demand of high-demand goods is given by /Vm; and the total demand of low-demand goods is given by sN(M - m). Thus, aggregate profits of high-demand manufacturing firms are given by
And aggregate profits of low-demand goods are given by
The market structure of manufactured goods in this model resembles monopolistic competition; in this case, however, prices and consumptions are predetermined. Since market entry and exit are assumed to be free, prices should be set for all manufactured goods such that profits are null everywhere: i = II = 0. Hence, the equilibrium prices of high-demand manufactured goods and low-demand manufactured goods, p and P, should satisfy the following equations:
and
These equilibrium conditions imply that prices of low-demand manufactured goods are higher than prices of high-demand manufactured goods: P > p. This outcome is explained by the fact that a common fixed investment per sector implies higher average fixed costs for low-demand goods than for high-demand goods.
Because of the consumption rigidities, this economic system does not guarantee equilibrium in the factor markets. In any case, aggregate capital demand, Ke, cannot exceed capital supply, K:
Additionally, aggregate labour demand cannot exceed labour supply:
All parameters denoted with Greek letters are assumed to be constant: the agricultural multifactor productivity (α), manufactures' marginal costs (β), manufactures' fixed costs (Φ), the minimum food requirement per capita (y), and the fraction 0 of the utility function. The population (N), the capital stock (K), and the population fraction of capitalists (s) are also given. Hence, the economic system has eleven unknown variables: w, r, F, KF, LF, p, P m, M, k e , and Ke. With nine equations and two inequations, a general equilibrium might exist if the slackness is supressed (the labour market and the capital market clear). Unfortunately though, the solutions are mathematically intricate. Numerical solutions may be found, however, by means of an electronic spreadsheet package.
Finding Solutions
From a mathematical viewpoint, the economic system has some degree of recur-sivity. Taking into account that wages are limited by agricultural productivity (0 < w < a), the arbitrary choice of w within this interval immediately determines the user cost of capital, r, by equation (1). Given w and r, the prices p and P for high-demand and low-demand manufactured goods are determined by equations (8) and (9).
Given w and p, the diversity of manufacturing consumption by a typical worker, m, is determined by equation (4). The combination of equations (5), (6), and (10) yields solutions for the effective capital demand per capitalist (k e ), the aggregate effective capital demand (K e ), and the diversity of manufacturing consumption by a typical capitalist (M).3 The key variable here is the capital demand per capitalist, k e , since, in any case, it cannot overcome the available capital per capitalist: i.e. ke ≤ k, where k ° K/(sN). Whenever capital demand exceeds capital supply, the last variable, i.e. k, is used in the equation system. Given the previously mentioned variables aggregate food demand, F, is solved by equation (7), and factor demands in the agricultural sector, K F and L F , are also solved by equations (2) and (3). Finally, the gross domestic product is defined as follows GDP = F + pNm + PsN(M - m).
First case: Extent of the Market Constraint by Lack of Population
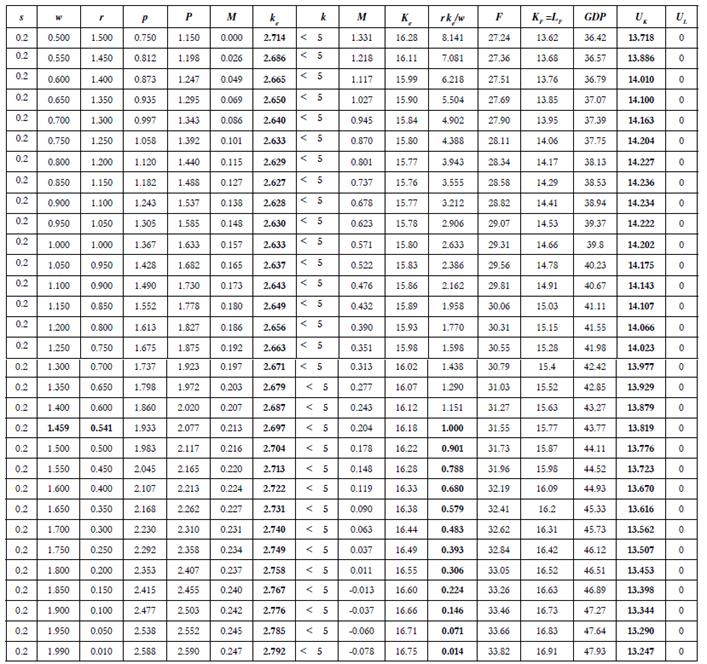
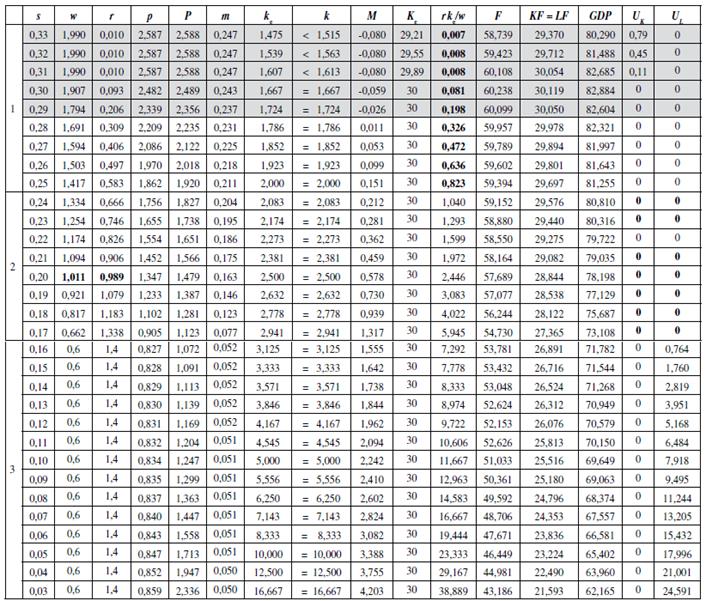
In the first case that is examined below, the general economic equilibrium is looked for the following specific parameters: α = 2; β = 1.3; y = 0.5; Φ = 2; and θ = 0,75. It is also assumed that the capital stock and the population are given by K = 30 and N = 30. It is expected that the population fraction of capitalists is given by s = 0.2 (20%): only one of every five people is a capitalist. Thus, the market is too small. As Table 1 shows, there is no wage between the minimum subsistence remuneration (the wage that just buys the minimum food demand: y = 0,5) and the maximum wage (α = 2) that provides full capital employment (U K > 0).4 Labour supply is fully employed (UL = 0).5 Notice that the factor price adjustment does not work: for a capital user cost lower than r = 0,541 (a wage higher than w = 1,459) the typical capital remuneration falls below the wage: rke/w < 1. Moreover, in this particular case, even the minimum user cost of capital (r = 0,01), or the maximum wage (w = 1,99), does not clear the capital market: effective capital demand is always lower than capital supply. Therefore, the lack of aggregate demand due to the low population size prevents an economic equilibrium. The industrial economy cannot take off, capital profitability collapses, and all factors are completely assigned to the agricultural sector. With a constant returns to scale technology, the agricultural sector may accommodate the productive factors if they are of the right proportions (1 to 1 in this case); but the increasing returns to scale technologies of the manufacturing sector requires a minimum demand level in order to cover fixed costs.6
Second Case: Extent of the Market Constraint by Excessive Capital Concentration
The analysis moves on to consider different levels of capital concentration under the assumption of market clearing for goods and factors. In this new case, the population has doubled: N = 60, but all other parameters are set just as before. Table 2 shows the numerical results. With a higher market demand, there appear some price remunerations for labour and capital that determine a general economic equilibrium. As a matter of fact, when the population fraction of capitalists is given by s = 20%, as in the previous analysis, a general economic equilibrium might be achieved with the following couple of factor prices: w = 1,011 and r = 0,989 (see Table 2). This equilibrium is unique. Notwithstanding, general equilibrium is not guaranteed since capital property concentration might become a relevant constraint for economic activity.
Table 2 Extent of the Market Constraint by Excessive Capital Concentration Parameters: α = 2; β = 1,3; γ = 0,5; Φ = 2; θ = 0,5; K = 30; N = 60.
Source: own elaboration.
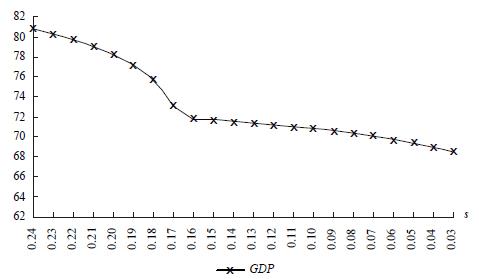
Table 2 focuses on the equilibrium results of an economy under a growing degree of capital property concentration (s, the population fraction of capitalists, is ordered from high to low values). This is just comparative statics; s is assumed to be predetermined in the period of analysis. Thus, Table 2 does not describe a capital concentration process throughout time; it just considers a big range of possibilities for s. The table shows that this market economy requires some minimum level of capital property concentration: for s > 0,24 (24%) the remuneration of the typical capitalist is lower than the wage: rk c /w < 1. Hence, low levels of capital concentration, as in the first frame of Table 2, are not suitable for capitalist activity: an original capital accumulation process is unavoidable. Moreover, for very low levels of capital property concentration, as in the shadowed section in frame 1: s ≥ 29%, capital remuneration is so low that the model yields a negative consumption of manufactured products by capitalists; although this is not a viable economic outcome, it is reported here in order to exhibit the workings of the model. Therefore, in this model capitalism requires some minimum capital property concentration. Moreover, the second frame of Table 2 reveals that a full general market equilibrium may occur for intermediate levels of capital property concentration (24% ≤ s ≤ 17%); in these circumstances unemployed labour and unemployed capital are nil: U L = U K = 0. Finally, the third frame of Table 2 shows that under a high degree of capital concentration (s < 17%) the effective capital demand exceeds capital supply: kc > k, and labour unemployment is unavoidable (U L >0).
The price adjustment works for frames 1 and 2 in Table 2. Under these circumstances (low and intermediate levels of capital property concentration: s > 17%), the economic logic is as follows: a higher capital concentration (si) increases labour supply [L = (1 - s)NT], concentrates capital and income in the hands of capitalists, lowers aggregate demand (GDPI), and the adjustment comes with a lower labour remuneration (wl) as well as a higher capital remuneration (rt). A lower wage is required in order to expand labour demand so that the labour market equilibrium is preserved.
Furthermore, under a high degree of capital concentration (frame 3 in Table 2) the working of the economic system is modified. All capital is fully employed (U K = 0), but there is always some labour unemployment (U L > 0).7 This last feature is due to the lack of aggregate demand. And the price adjustment does not work: lower wages just diminish aggregate demand and increase unemployment; and higher wages -which would go some way to solving the economic disequilibrium by increasing aggregate demand- are not viable due to the excess of labour supply. Thus, the price system of the labour market collapses under extreme capital concentration. In this situation, the wage's cost effect is overcome by the wage's income effect. Without government intervention wages would probably be set at the subsistence level (w = y = 0.5) or even below, but the setting of a minimum wage above the subsistence wage prevents a collapse of the level of economic activity. This feature is explicitly considered in the third frame of Table 2: when capital concentration is high (s < 17%) the wage is fixed at w = 0.6 so that workers might consume some manufacturing goods (w > y = 0.5). Graph 1 depicts that, under high capital concentration, the setting of a minimum wage prevents economic activity to fully plunge compared to the alternative of allowing the wage to fall freely.8
Table 2 also reveals that the level of economic activity always decreases with a growing degree of capital property concentration (lower s) as a consequence of a lower aggregate effective demand. This is shown clearly by the Graph 1 for degrees of capital property concentration which are consistent with general market equilibrium (24% ≥ s ≥ 17%). The same result would more strongly apply for a high degree of capital property concentration (s < 17%) if the governmet does not fix a minimum wage, as depicted by Graph 1.
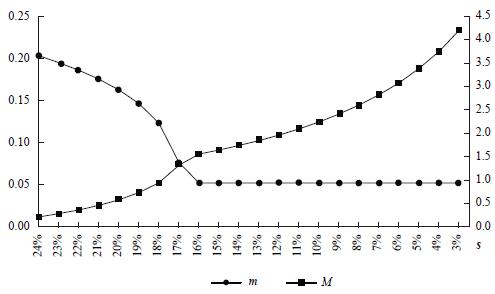
Income inequality, however, keeps increasing. This result is explained by the expansion of capitalist consumption diversity (M increases) since the worker's consumption diversity is unchanged (m is constant under the assumptions of a minimum wage and high capital property concentration). Graph 2 depicts these features. Therefore, setting a minimum wage under high capital concentration is not only favourable to workers but also to capitalists.
Source: own elaboration.
Graph 2 Manufacturing Diversity across Social Classes vs. Capital Concentration
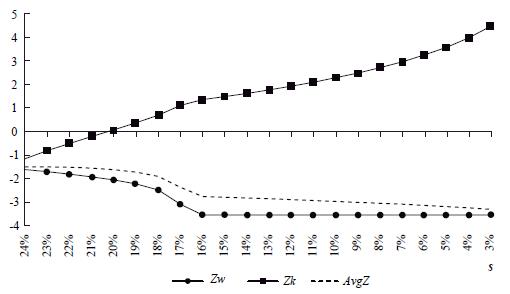
The evolution of welfare for a typical worker and a typical capitalist is depicted by Graph 3. As a general result, a growing degree of capital concentration worsens the welfare of workers, as measured with the utility function (Zw), until the minimum wage is reached: under this circumstance, a worker's welfare index remains constant at a low level. On the other hand, the welfare of the typical capitalist (Zk) increases systematically with capital concentration. Since a higher capital concentration implies a growing fraction of population workers, the average welfare, AvgZ, which is depicted by the discontinuous line in Graph 3, decreases with capital concentration.
Although workers find a low and stable welfare path when they earn the minimum wage, equity is compromised because of the growing welfare gap between workers and capitalists in an environment with a growing concentration of capital property.
An Additional Result
Under circumstances of full market equilibrium (intermediate case which was examined above) and the assumption of ceteris paribus, a higher agricultural productivity (α↑) increases wages (w↑), improves labour diversity of manufacturing consumption (m↑), diminishes income inequality (rk e /w ↓), and strongly expands the gross domestic product (GDP ↑). Table 3 exhibits these results.
Therefore, this model shows that a country with unexploited land or low technological productivity might achieve enormous gains through a land reform and heavy investment in science and technology applied to agricultural and agroindustrial activities.
Summary and Final Remarks
This is a static model and so it is unable to address the important issue of economic growth. It focuses on the impact of the population's purchasing power on the level of economic activity. In order to do so, a multi-sector model was built for which constant returns to scale are assumed in the food sector and increasing returns to scale are assumed in the manufacturing sector. Some minimum level of food consumption is required for every person; every individual satiates his/her need for each manufactured product with just a single unit, but the marginal utility decreases with the number of manufactured products consumed (consumption diversification has a marginal decreasing utility).
The implications of this model for economic growth can be found in the transmission mechanism by which productive activity is transformed into income and market demands. The extent of the market matters for economic activity: 1) a low population size does not generate enough aggregate demand for the capitalist economic to take off (see Table 1); 2) even if the market size is high, a low level of capital property concentration is not consistent with profitable capitalist activity: some original capital accumulation is required (see frame 1 in Table 2); 3) if the last two conditions are satisfied (capitalism works), a growing capital property concentration lowers wages, increases the shortage of effective demand, and diminishes economic activity (see frames 2 and 3 in Table 2); 4) finally, if capital property concentration exceeds some critical level, the price system fails to equilibrate the labour market, and some labour unemployment is unavoidable (see frame 3 of Table 2). Thus, for high levels of capital property concentration, the labour market does not adjust and the labour remuneration tends to fall. This result just worsens the lack of effective demand and lowers the GDP even more. The disequilibrium in the labour market justifies setting of a minimum wage.
If, as some authors argue, the capitalist regime has an intrinsic trend toward capital property concentration (Marx; 1867; 1885; and 1894; Piketty, 2013), it seems sensible to assume that sooner or later the economy will reach a degree of capital property inequality such that unemployment is unavoidable. This is presumably an environment prone to economic crisis. Notwithstanding, as Marx pointed out, some minimum level of labour unemployment might be necessary in the capitalist regime in order to offset the wage pressures derived from a growing labour organization: this is the industrial reserve army's famous hypothesis. Thus, a slightly high degree of capital property concentration may be functional to capitalist society.
It seems, however, that the trend towards capital concentration does not stop in sensible levels. On the contrary, wealth concentration has been increasing all over the world, and this trend shows no sign of being reversed.9 This model, however, does not support State-sponsored capital expropriation. Instead, it finds that under some intermediate levels of capital concentration the economic system may operate with full market equilibrium; this may well be the secret of the virtuous capitalist economies in northern Europe.
The economic system analyzed here reveals that, after some minimum degree of capital accumulation, wealth concentration is always convenient to capitalists but diminishes aggregate demand and the economic activity level. Under the assumptions of free mobility of factors, flexible prices and market clearing, supply creates its own demand, but the creation rate decreases with the degree of capital property concentration. However, for high degrees of capital concentration, the price system collapses as economic regulator, and Say's law consequently collapses: an unregulated price system does not provide the basis for economic equilibrium (supply does not necessarily create its own demand).10
The government, as a social welfare guardian, might require income redistribution policies to be adopted, and it even ought to take wealth redistribution measures if productive wealth is highly concentrated or missused and wasted in speculative rental activities. It might be important as a future research to inquire about the economic impact of an unemployment insurance program.