Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.20 Bogotá Jun./Dec. 2004
A note on some properties of an efficient network resource allocation mechanism
Nota sobre algunas propiedades de un mecanismo eficiente de asignación de recursos en redes
Fernando Beltrán
ISOM Department Faculty of Business and Economics, University of Auckland
f.beltran@auckland.ac.nz
Recibido el 30 de septiembre de 2004, aprobado el 8 de octubre de 2004.
PALABRAS CLAVES
Distribución de recursos en redes, subastas de ancho de banda, precios por congestión.
RESUMEN
Presentamos algunas propiedades límite de un mecanismo de asignación de recursos en redes conocido como la Subasta Progresiva de Segundo Precio (PSP). Este mecanismo busca asignar eficientemente recursos de red tales como ancho de banda y capacidad de buffer, en un ambiente caracterizado por usuarios que compiten; la subasta PSP busca resolver, o al menos aliviar, la congestión en una red exigiendo un intercambio de información entre el subastador y los usuarios sin mucha carga de señalización, y resolviendo el problema de la asignación de un recurso (teóricamente) infinitamente divisible. La regla de asignación está inspirada en la subasta de segundo precio (Vickrey). Nuestro análisis de la subasta PSP explora sus propiedades límite, por ejemplo, cómo cambia la asignación en la presencia de un conjunto polarizado de usuarios. Esto último se refiere a una situación en la que los usuarios se dividen en dos grupos: unos con alta demanda y baja valoración por el recurso y otros con baja demanda y alta valoración. Mecanismos tales como las subastas se han vuelto muy populares para la asignación de recursos en redes que presentan congestión, tales como el acceso a servicios Internet.
KEY WORDS
Network resource allocation, bandwidth auction, congestion prices.
ABSTRACT
We present some limiting properties of a network resource allocation mechanism known as the Progressive Second Price (PSP) auction. This mechanism aims at efficiently allocate network resources, such as bandwidth or buffer capacity, in an environment characterized by competing users; the PSP auction seeks to solve or at least to ameliorate congestion in a network demanding a low signalling burden between the auctioneer and the users, and solving the allocation problem of an (theoretically) infinitely divisible resource. The allocation rule is inspired in the second price (Vickrey) auction. Our analysis of the PSP auction explores its limiting properties, namely, how the allocation changes in the presence of a polarized set of users. A polarized set of users is a mixture of users of two types: high valuation, low demand users and low valuation, high demand users. Mechanisms such as auctions are becoming increasingly popular to handle the resource allocation problem in networks facing congestion, such as the access to Internet-based services.
INTRODUCTION
A key aspect in the development of the Internet access market and, consequently, the commercial use of broadband IP applications is the issue of efficient allocation of networks resource, more specifically bandwidth. If the fact that many users trying to gain access to a - frequently- scarce resource, induces congestion in the network, then there is a need for a market approach to pricing of congestion in Internet. Negative externalities arise when resources such as bandwidth and buffer space are shared by users unable to coordinate their actions. Therefore, the network administration should consider an efficient allocation of resources in order to share dispersed resources among users who are also dispersed. Besides, as networks incur in costs to deliver their services, pricing serves a double purpose of cost recovering and, hopefully, efficient allocation.
This note presents a brief overview of selected sources of the literature on pricing network resources under congestion. The latter serves the main purpose of studying some limiting properties of a theoretical mechanism for pricing under congestion: the Progressive Second Price (PSP) auction [Semret, 1999]. The methods in the literature seemed to have evolved from some purely engineering-oriented whereby central control is the key, up to methods that acknowledge the complex characteristics of economic agents competing for resources in the context of access to bandwidth and that use the principles of a branch of economics called mechanism design. The analysis of the auction explores some of the limiting properties of the PSP auction, namely, how the allocation changes in the presence of a polarized set of users. A polarized set of users is a mixture of users some of which have a high demand but a low willingness to pay per unit of the resource and others whose demand is relatively low with a higher per unit willingness to pay.
1. ENGINEERING APPROACH TO PRICING
The goal of an efficient network resource pricing mechanism is to optimally allocate network resources among users while both satisfying their needs and controlling congestion. A formidable challenge to ISPs and other sellers of networks access is to design a price scheme that solves or at least ameliorates congestion, which is responsible for delays and degradation of a network's overall performance. In the presence of network congestion, users would prefer to adjust their demand for capacity. Nevertheless, Internet has not provided economic but engineering tools to solve for network resource allocation. Users of Internet pay a flat rate for access, regardless of their traffic patterns or quality of service needs. As long as traffic grows and congestion becomes a sensitive issue, more and more users would be willing to pay differentiated rates for differentiated services
The technical literature introduces several pricing schemes, which are described below. The most prevalent of the pricing schemes is the flat rate, by which any user will pay a fixed amount for a fixed bandwidth (Bailey, 1999). Congestion is dealt with on a "best effort" basis in accordance to the Transmission Control Protocol (TCP). One of the most important effects of such tariff policy is the network externalities, which stimulate the growth in connections and consequently in traffic. On the other hand, billing costs to the provider are kept low.
Clark (Clark, 1995) has proposed to distribute the main features of the service, such as capacity, among the users based not on guarantees but on expectations; since it would be useless to guarantee a given performance level during a certain time of the day, it would turn out to be more logical to think of the performance a user would expect from the network service. Such performance is defined as the largest amount of information a user would send constrained to a preset latency at a given transference rate.
Cost-based priority-based pricing was originally proposed by McLean and Sharkey (McLean and Sharkey, 1994), using Aumman-Shapley prices and the Shapley value to find access prices as a function of the users' transfer rates in an architecture model that uses a first-in first-out (FIFO) priority queue model. A paper extending the use of cooperative games shows (Beltrán and García, 2001) the feasibility of obtaining congestion dependent prices in a network, establishing simultaneously different quality-of-service levels among the users. This approach recognizes and quantifies the effects of congestion, efficiently allocating the cost of congestion to users.
2. MARKET APPROACH TO PRICING
A different approach is taken by the DifffServ architecture model which intends to address the issue of providing quality of service (QoS) guarantees to multiple sources of traffic. The basic idea behind the Diffserv model is to decentralize QoS provision to the level of independent domains, each with a "bandwidth broker" (Parameswaran et al., 2001). Such broker makes admission decisions of applications based on local allocation policies and once the application is accepted, the broker marks each packet as belonging to one of a handful of classes.
A new trend in pricing is the introduction of usage-based charging schemes (Tuffin, 2001); several works consider the users' willingness to pay and the congestion of the network; more precisely they propose that transfer rates be adjusted according to such considerations (Kelly, 1998). Another solution, which includes auctioning for priority, is the "smart market" approach (McKie-Mason and Varian, 1994). This approach is incentive compatible in that a user sets the bid price in each packet equal to her true valuation, implying the lowest possible information requirement. Nevertheless, the engineering costs of sorting packets by bid price and other functions are very high, rendering the mechanism not feasible for implementation under current technology.
Some recent literature addresses the issue of auctions for bandwidth instead of dealing with auctions for individual packets (Lazar and Semret, 2001), (Semret, 1999) (Semret et al., 1999) (Semret et al. 2000). Such works introduce the use of auctions for sharing network resources.
3. THE PROGRESSIVE SECOND PRICE (PSP) AUCTION
Semret (Semret, 1999) proposes a game theoretic approach to the objective of a more efficient and fair utilization of shared resources; such approach, called networking games, results in mechanisms where intelligence and decision making is distributed. In a network the interacting agents acquire resources from the network on behalf of applications which need bandwidth and buffer space. Outcomes as efficient as those of a central controller may be collectively achieved if appropriate rules of interaction are introduced. Semret proposes that pricing can be resolved within the engineering of the network, overcoming the ex-post price structure generally imposed on most networks; his mechanism is called the Progressive Second Price (PSP) auction.
PSP is based on two aspects of mechanism design (Williams, 1986): realization and Nash implementation. Realization means the design of a message process (exchange of information between agents and the centre) enabling the achievement of a certain objective. Nash implementation means that allocation rules are designed with incentives, driving the players to equilibrium where the desired allocation is achieved.
An interesting, and economically attractive characteristic of PSP is that "the exchanged messages are as small as possible, while still conveying enough information to allow resource allocation and pricing to be performed without any a-priori knowledge of demand, and the amount of computation at the center is minimized" (Semret, 1999).
The auction consists of players submitting bids (a player i declares his desired shared q i of the total resource and a price pi he is willing to pay for it) and the auctioneer allocating shares of the resource to the players based on their bids. The PSP auction allocation rule assigns player i a bandwidth which is equal to the minimum value between his capacity bid, q i, and the remaining capacity resulting from the total capacity Q minus the sum of all those capacity bids, q k, whose price bids are greater than or equal to i's price bid, that is, p k > pi. In other words, the allocation rule is:
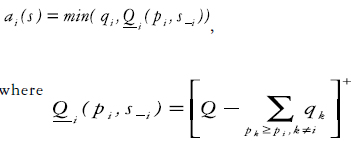
and s = (pi, ) represents the set of biding prices by i - pi - and by the rest of the players - s-i.
The cost to any agent i is the sum of the products of each price bid made by every agent j (different from i) times her incremental allocated capacity, that is, the difference between the capacity allocated to j, if j were not participating, and her allocated capacity when he participates. In other words, the pricing rule is:
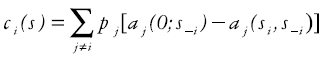
As Semret puts it, (Semret, 1999) in a PSP auction what a player pays for his allocation is covering the opportunity cost incurred at by the exclusion of those bidders due to i's bid. In a way, the mechanism "compensates" the auctioneer for any losses he might have when not allocating any part of the resources to those who have "lost" the auction to i.
4. AN EXAMPLE OF THE APPLICATION OF THE PSP AUCTION
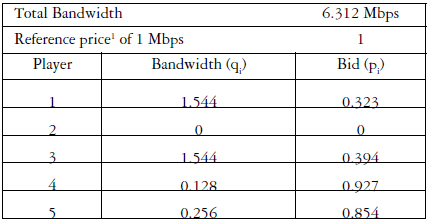
We can illustrate how PSP works with a simple example, where 5 potential users contend for bandwidth owned by an ISP. The ISP has a T2 channel, able to deliver at 6.312 Mbps. As an illustration of a case when no congestion charges are levied, consider only 4 users as shown in Table 1. As can be seen, the aggregated demand, 3.472 Mbps, does not exceed the total capacity of the channel. Therefore each player gets the capacity that he requires and the congestion price charged is zero.
Table 1
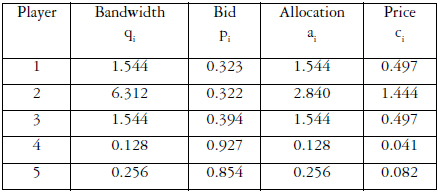
If the channel was to be shared by the same users plus a new one demanding the whole T2 capacity, that is, player 2 asking for 6.312 Mbps at a rather low price -one that is barely matching the lowest existing bid-, the bandwidth allocated to each player and the charges would vary as shown in Table 2.
Table 2
The total bandwidth allocated is the total available, and the lowest bid gets only a fraction of its demand.
The example here illustrates a situation where the set of users is a mixture of some users with a high demand but a low per-unit willingness to pay for the resource and others whose demand is relatively low with a higher per-unit willingness to pay. In some sense we can say that the set of users is polarized. This could be interpreted as a case in which an access provider has two types of customers: retail customers and access resellers.
Let us see what would happened if, in the process of seeking for more capacity, player 2 decided to bid higher while the other bidders' bids remained the same. After all, they are getting what they want and player 2 is not.
Charts 1 and 2 show how the auctioneer would allocate bandwidth and price to each player, had player 2 changed her (initial) bid. This analysis is based on comparative statics and is not aimed at finding equilibriums. Semret (Semret, 1999) shows how players adjust their bids to get a new equilibrium whenever an existing equilibrium is disturbed by an action (a new bid) of one of the players and the auctioneer changes the allocation accordingly.
Chart 1: Bidders´ allocated bandwidths change when player 2 decides to change her bidding price. All other bids remain constant.
Chart 2: Bidders´ allocated prices change when player 2 decides to change her bid. All other bids remain constant. (Prices for players being excluded are defined by the auction in spite of not being allocated any bandwidth; in such case one can interpret such price as one that would be charged to a player if she increased her bid and beat her nearest wining rival).
Our intention here is to illustrate the effects of different bids by a player whose characteristics resemble those of a reseller or access provider. The results show that player 2 must beat higher valuations, expressed in her competitor's bids, if she wanted a bigger portion of the resource. Such result is not surprising; however, it is an interesting feature of the PSP auction to observe that as long as player 2 matches subsequent higher bids, PSP punishes those bidders whose bids are equal2. Once player 2's bid overpasses a rival bid, the latter gets excluded. The prices observed seem to reflect the exclusion-principle, which states that 2 is covering the declared willingness to pay of those being excluded.
In the context presented here, it is worthwhile mentioning that one possible drawback of the mechanism is the exclusion of high-demand users -resellers and access providers- in favour of low-demand users as long as the latter's bids are high enough. It is possible that such costs have an effect on the price quoted to the final users of the access provider.
5. THE DESIGN OF AN ALTERNATIVE MECHANISM
The PSP auction is a very ingenious mechanism inspired in the Vickrey auction with the additional feature that its computation is not expensive. Furthermore, it does not impose a high information burden on users and, therefore, it becomes a very attractive idea as a market-oriented mechanism that is incentive compatible and individually rational (Semret, 1999).
At the centre of the design problem, lies the issue of whether a pricing mechanism can be realistically implemented given the complexities inherent to achieving efficiency and Nash implementation (Williams, 1986). PSP aims at solving the complexity, brought into the mechanism design process by the structure of the message sent from a player to the auctioneer. In fact, PSP achieves the economic objectives of incentive compatibility and efficiency, while demanding a small signalling load and a computationally simple allocation rule (Semret et al., 2000).
There is a key aspect in making a pricing mechanism attractive to a network resource seller: how well it does away with revenues. The PSP auction does not seem to address such issue since it focuses on achieving incentive compatibility and simplicity in computation and signalling. In spite of its simplicity, the PSP auction only allows the exchange of messages that reflect how much a user values a given amount of bandwidth; after all, it is common that a user is just trying to get a much defined amount of bandwidth. One can wonder whether allowing users to express their bids as a continuous function of bandwidth, might improve the trade-off between maximizing the auctioneer's revenue and achieving efficiency while keeping the message process as simple as possible.
One way to start is to think of the message process as a pair (a, b), which indicates the intersect (a) and the slope (b) of an affine function representing the user's demand function. Thus, any user would reveal her willingness to pay for different amounts of bandwidth, letting her reflect changes in her valuation (marginal valuation) for different units of the resource. This might reflect the fact that the user has a certain degree of flexibility on her demand for bandwidth, and is not committed to a unique amount.
FOOT NOTES
1. In this example price is not given in any actual currency; prices are quoted in relation to a representative unit price per Mbps.
2. Notice how, when several bids tie, the total bandwidth allocated is not the total bandwidth offered.
BIBLIOGRAPHIC REFERENCES
[1] Bailey, J., J. Nagel, and S. Raghavan. Ex-Post Internet Pricing. Working paper. University of Maryland, 1999. [ Links ]
[2] Beltrán, F and C. García. "Aumann-Shapley and Shapley value-based priority pricing: an approach to congestion control in data networks". En CGSR, Universidad de Los Andes. http://cgsr.uniandes.edu.co 2001. [ Links ]
[3] Kelly, F.P., A.K. Mauloo, and D.K.H. Tan. "Rate Control in Communication Networks: Shadow Prices, Proportional Fairness and Stability". En Journal of the Operational Research Society, 49:237-252, 1998. [ Links ]
[4] Lazar, A.A. and N. Semret. "The Design and Analysis of the Progressive Second Price Auction for Network Bandwidth Sharing". En Telecommunication Systems, Special Issue on Network Economics, 2000. [ Links ]
[5] McKie-Mason, J.K., and H.R. Varian. Pricing the Internet. In B. Kahin and J. Keller, editors, Public Access to the Internet, Prentice Hall, 1994. [ Links ]
[6] McLean, R. and W.W. Sharkey. "Alternative Methods for Cost Allocation in Stochastic Service Systems". En Brazilian Electronic Journal of Economics. Vol. 1, No. 1, 1997, http://www.beje.decon.ufpe.br [ Links ]
[7] Parameswaran, M., J. Stallaert, and A.B. Whinston. "A market-based allocation mechanisms for the DiffServ framework". En Decision Support Systems, 31, 351-361, 2001. [ Links ]
[8] Semret, N. Market Mechanisms for Network Resource Sharing. Ph.D. Thesis, Columbia University, 1999. [ Links ]
[9] Semret, N., R.R.F. Liao, A.T. Campbell, and A.A. Lazar. Market Pricing of Differentiated Internet Services. Proceedings of the 7th International Workshop on Quality of Service, 1999. [ Links ]
[10] Semret, N. R.R.F. Liao, A.T. Campbell, and A.A. Lazar. "Pricing, provisioning and peering: Dynamic markets for differentiated Internet services and implications for network interconnections". En IEEE Journal on Selected areas of Communications, 18(12):2499-2513, 2000 [ Links ]
[11] Tuffin, B. "Revisited Progressive Second Price Auction for Charging Telecommunication Networks". En INRIA Rapport de Recherche No. 4176. May 2001. [ Links ]
[12] Williams, S.R. "Realization and Nash Implementation: Two Aspects of Mechanism Design". En Econometrica, Vol. 54, No. 1, 139-151, 1986. [ Links ]