Un modelo de lógica difusa y conjuntos difusos para el pronóstico de los niveles medios diarios del río Magdalena, en la estación limnigráfica de Puerto Salgar, Colombia

A model of fuzzy logic and fuzzy sets to the prediction of daily average levels of the Magdalena River, in Puerto Salgar, Colombia

John Alexander Segura Bolívar
Ingeniero civil. Grupo de investigación Hidrociencias, Pontificia Universidad Javeriana. Grupo de investigación en ingeniería de recursos hídricos, GIREH, Universidad Nacional de Colombia.

Nelson Obregón Neira
Ingeniero civil. Magíster en Ingeniería Civil con énfasis en ingeniería de recursos hídricos, Universidad de los Andes; PhD en hidrología, University of California at Davis. Profesor asociado, Director Grupo de Investigación "Hidrociencias", Director Maestría en Hidrosistemas, Facultad de Ingeniería, Pontificia Universidad Javeriana. Profesor catedrático, Facultad de Ingeniería, Universidad Nacional de Colombia.

Recibido 10 de septiembre de 2005, aprobado 28 de octubre de 2005.

PALABRAS CLAVES
Pronóstico, nivel, río Magdalena, sistema de lógica difusa basado en conocimiento, juicios de expertos, símplex descendente multidimensional, ameba.

RESUMEN
El pronóstico de niveles diarios de ríos en Colombia se reporta oficialmente en términos lingüísticos. Este hecho inspiró un modelo basado en la teoría de conjuntos difusos, concepto proveniente de la inteligencia artificial. Un Sistema de Lógica Difusa (SLD) permite analizar observaciones en el tiempo clasificándolas en categorías lingüísticas, aproximadas a la calificación empleada o a la manera en que una persona describiría el fenómeno. Usando juicios de expertos se estima el nivel del día siguiente. Para la calibración del modelo se implementó un algoritmo de optimización global denominado Símplex Descendente Multidimensional (SDM).

KEY WORDS
Forecasting, stage, Magdalena river, knowledge-based fuzzy logic system, experts' judgements, multidimensional downhill simplex, amoeba.

ABSTRACT
Forecasting of diary stages of rivers in Colombia is reported officially in linguistic terms. This fact inspired a model based on theory of fuzzy sets, concept coming from artificial intelligence. A Fuzzy Logic System (FLS) allows to analyze observations in time classifying them in linguistic categories which are approximated either to the employed qualification, or to the way in that a person would describe the phenomenon. Taking into account experts' judgements the level of the following day is estimated. An algorithm of global optimization named Multidimensional Downhill Simplex was implemented in order to calibrate model parameters.

1. INTRODUCCIÓN

La Lógica Difusa (LD) apareció en 1965 cuando Lofti Zadeh publicó el artículo Fuzzy Sets (Altrock, 1995; Bojadziev, 1995; Cox, 1998; Klir, 1995; Lobrecht, 1999; Maskey, 1998). Hacia 1977, E. Mamdani desarrolló una aplicación para un generador de vapor que no podía funcionar bajo técnicas convencionales. Posteriormente se masificó y comercializó en Japón (Fuji Electric, planta de tratamiento de aguas, 1983; Hitachi, sistema del tren subterráneo, 1987) (Altrock, 1995; Cox, 1998, Klir, 1995).

Ha sido probada en diversos campos de la ingeniería y ha llegado a usarse en toma de decisiones, ecología y psicología. Como un modelo de sistema inteligente es una combinación de los sistemas basados en reglas (estudiados dentro de los sistemas basados en el conocimiento) y de la inteligencia computacional que abarca a las redes neuronales. Se puede emplear en cualquier área de control inteligente o procesamiento de datos en tiempo real. En este estudio se aprovecha la versatilidad de la LD para manejar información adquirida a través del conocimiento, ya sea empírico o científico.

Una persona que a diario recorre el río Magdalena y habita en la zona puede desarrollar habilidad y precisión para pronosticar tal como lo haría una persona especializada en modelos hidrométricos. Ambas personas son expertos: mientras el primero, a partir de su experiencia pronostica luego de observar el cielo: "al sur (de Puerto Salgar) está lloviendo bastante entonces mañana podré transportar el plátano"; el segundo busca herramientas para convertir aquéllas sentencias en números indicadores del comportamiento del río dentro de un modelo y, finalmente, encontrar el nivel del río expresado en un número. Por su parte, el IDEAM (IDEAM, 1964- 2004) presenta reportes de la siguiente manera: a) el nivel del río Magdalena en la parte alta y media registra fluctuaciones moderadas en los niveles con tendencia leve al descenso, y en la cuenca baja, registra una tendencia continua al ascenso, los valores en el rango alto; b) en Puerto Salgar, el nivel del río Magdalena presenta moderado descenso, con valores en el rango alto (IDEAM; Rivera, 2004). Estas son proposiciones que usan modificadores lingüísticos (Bojadziev, 1995; Klir, 1995) sobre la variable nivel, los cuales califican los registros esperados de manera similar a la planteada en un sistema basado en el conocimiento (Obregón, 2002).

2. CONCEPTUALIZACIÓN DEL MODELO

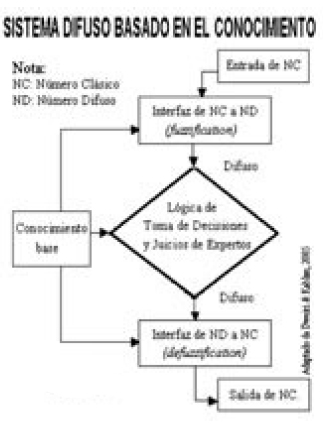
La entrada y salida de un SLD puro son conjuntos difusos. En el caso de un SLD tipo Mamdani, éste puede trabajar, además, con entradas y salidas reales. Está compuesto por una base de reglas, un sistema de inferencia y dos componentes para manejar entradas reales y difusas: las interfaces fuzzicación y defuzzicación (ver Fig.1). La primera establece una aplicación entre los números clásicos en el dominio de las entradas del sistema y los conjuntos difusos en el mismo universo de discurso. La segunda realiza la operación inversa entre conjuntos difusos en el universo de discurso de las salidas. Sus ventajas son: la posibilidad de incluir conocimiento experto en forma de reglas lingüísticas y la oportunidad dada al usuario de elegir la interfaz fuzzificación y defuzzificación para adaptar fácilmente el problema real a modelar. De esta forma, las series de tiempo diarias son los datos de entrada que luego se ensamblan con la información basada en el conocimiento por las reglas de experto, y éstas, junto con el algoritmo de calibración, condicionan la salida de la serie simulada que se quiere obtener.

Figura 1.

2.1. HERRAMIENTAS INFORMÁTICAS

Se usó el lenguaje Matlab® el cual es bastante funcional y contiene un paquete de Lógica Difusa (MathWorks, 2004). Los códigos se desarrollaron empleando un programa principal y subrutinas para ejecutar cálculos y representar gráficos.

2.2. SERIES DE TIEMPO DE LAS ESTACIONES HIDROMÉTRICAS

Se estudiaron inicialmente cuatro series de niveles medios diarios y dos de precipitación media diaria elegidas para comparar sus características estadísticas aguas arriba y aguas abajo de la estación limnigráfica de Puerto Salgar (Segura, 2005) (Ver Tabla 1 y Fig. 2).

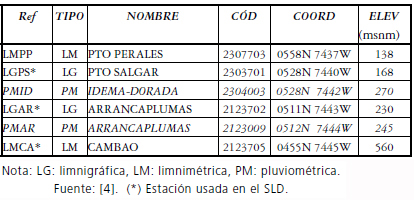
Tabla 1. Estaciones para estudio

Figura 2.

2.3. PROCESAMIENTO DE LAS SERIES DE TIEMPO

Para identificar las características comunes entre las series de tiempo diarias, se aplicaron dos tratamientos estadísticos: un análisis univariado lineal (Wilches, 2002) y un análisis bivariado lineal. Con esto se determinan las estaciones que se usan para el diseño del SLD.

El análisis univariado lineal se ilustra con la textura de la serie, el análisis de frecuencia, el autocorrelograma y el periodograma de cada serie. Las texturas de las series muestran complejidad en los datos. Para la construcción de los periodogramas fue necesario identificar los intervalos más largos sin datos faltantes en las series. Sin embargo, esto no representa problemas para el modelo ya que los datos que lo alimentan son patrones (ver sección 2.4.). En el periodograma LGPS se evidencia un armónico predominante para 44 días, similar al periodograma LGAR (Segura, 2005), mientras que en el periodograma LMCA hay dos armónicos dominantes para 5 y 12 días. Estos indicadores dan una idea aproximada del período en el cual existe mayor posibilidad de que se repitan los datos, y se podrían usar para pronosticar el nivel con una memoria de predicción correspondiente a ese número de días. Los periodogramas de las otras series no presentaron un armónico predominante, lo cual no necesariamente implica que se trata de un comportamiento caótico (Wilches, 2002). La función de autocorrelación decae rápidamente en todas las estaciones lo que permite deducir que se trata de datos secuenciales aleatorios.

En el análisis bivariado lineal se compara cada serie con la serie de interés LGPS. Las estaciones pluviométricas PMAR (e) y PMID (f) tienen correlación muy baja con LGPS, por lo tanto se descartan de los fines del planteamiento del SLD. La estacion LMPP (d) tiene un pequeño desfase en el primer corte con el eje de las abscisas que la diferencia del resto de las estaciones. Luego de la selección espacial previa de la estaciones, este trabajo se enfatiza en una elección basada en la similitud entre las correlaciones LGPS-LGAR (b), y LGPS-LMCA (c) permite concluir cuáles son las series que presentan características similares a LGPS, con las cuales se construye el SLD.

2.4 TOPOLOGÍA DEL MODELO DIFUSO.

Desde el aspecto topológico el SLD está conformado por tres variables de entrada: LMCA, LGAR y LGPS, y por una variable de salida LGPSsim, nivel del día siguiente simulado en Puerto Salgar.

Cada una de estas variables tiene su propia función de membresía, μ, compuesta por tres conjuntos difusos trapezoidales (los cuales se adaptaron mejor que otras formas de funciones de membresía examinadas) cuyos modificadores lingüísticos para Nivel desde el aspecto de navegabilidad son Intransitable, Riesgoso y Confiable (Segura, 2005). En cada una de las funciones de membresía se fijaron los valores extremos de los niveles máximos y mínimos históricos (NMáxH y NMínH) de cada estación relacionada de tal manera que los dos parámetros centrales de la función trapezoidal Riesgoso se convierten en incógnitas. Se supone que la configuración para LGPSsim es la misma que para LGPS. Entonces, el SLD tiene seis parámetros desconocidos.

En caso de liberar los extremos superiores (o inferiores), NmáxH (ó NMínH), el SLD tendría nueve incógnitas, y así sucesivamente (Segura, 2005).

Otro tópico importante del SLD son las reglas de expertos (Altrock, 1995; Bojadziev, 1995; Segura, 2005), con las cuales se determinan las implicaciones que pueden tener los cambios de las variables de entrada sobre la variable de salida, interconectados con términos lingüísticos. Para un sistema con n variables de entrada y m conjuntos difusos por cada variable de entrada se tienen mn reglas de expertos, las cuales son analizadas previamente por expertos en el tema del sistema a diseñar (Cox, 1998; Segura, 2005). Un ejemplo de regla de expertos es: Si el nivel del río en la estación limnimétrica de Cambao es intransitable y el nivel del río en la estación limnigráfica de Arrancaplumas es riesgoso, y el nivel del río en la estación limnigráfica de Puerto Salgar es riesgoso entonces el nivel del río en la estación limnigráfica de Puerto Salgar mañana será riesgoso.

En la anterior proposición el operador difuso mín (=and) filtra el menor de los números difusos resultantes de la fuzzificación de los valores que aporta cada variable (Altrock, 1995; Bojadziev, 1995; Cox, 1998; Maskey, 1998).. Se construye un resultado por cada regla y luego aplicando el operador max (=or) se obtiene el resultado difuso final que será deffuzificado a un resultado real por el método del centroide de área.

2.5. PATRONES DE ENTRENAMIENTO DEL SLD

La metodología para la generación de patrones de entrenamiento que alimenta el SLD es un proceso que requiere entender cuál es el dato que se desea pronosticar, teniendo en cuenta la memoria de predicción y la memoria de regresión del proceso. En este caso se desea obtener el nivel medio diario del río Magdalena en Puerto Salgar para el día siguiente (memoria de pronóstico = 1), teniendo los registros de los días actuales en cada variable de entrada (memoria de regresión = 1). En la Tabla 2 se puede apreciar la construcción de patrones para los registros entre el 24 de julio y el 1º de agosto de 1979. Para construir la tabla de patrones de entrenamiento aplicada en el presente modelo deben cumplirse simultáneamente dos condiciones: que para un día determinado no falte ningún dato de la terna LMCA, LGAR y LGPS, y que el dato del día siguiente en LGPS tampoco falte. En total se pudieron construir 7.832 patrones bajo estas condiciones. La ventaja de trabajar con patrones es que no se requiere suponer o sintetizar datos faltantes (sección 2.3.), ya que la idea es entrenar el sistema, es decir, que aprenda la configuración adecuada para cada caso.

2.6. CALIBRACIÓN. (AMOEBA)

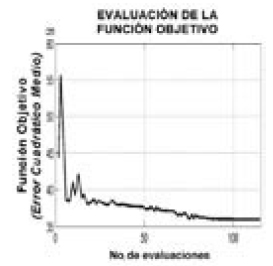
En la calibración se empleó el algoritmo optimización global Downhill Simplex Method (comúnmente llamado Amoeba) para minimizar funciones objetivo (Numerical, 1986 - 1992). En este caso, la función objetivo es el error cuadrático medio, EQM, el cual se calcula con los valores de las series real y simulada. El algoritmo se inicializa con un símplex de valores iniciales, predeterminados o supuestos, correspondientes a cada uno de los seis parámetros que se desean hallar (Segura, 2005). En la Fig. 2 se ilustra una de las ejecuciones del programa para apreciar cómo evoluciona el valor del EQM a medida que aumenta el número de evaluaciones de la función objetivo. Cuando se estabiliza EQM se han encontrado los parámetros cuyos valores producen el EQM más bajo.

3. ANÁLISIS DE RESULTADOS Y RECOMENDACIONES

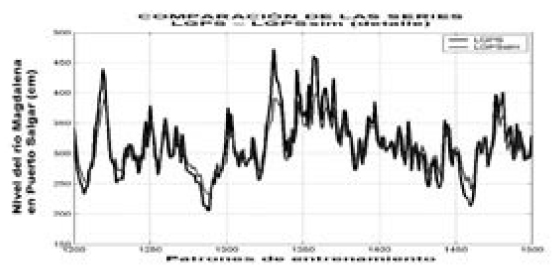
En la Fig. 3 se muestra un detalle de la comparación entre la serie real LGPS y la serie simulada LGPSsim obtenida con el SLD. Nótese que la textura de la serie simulada luce muy similar a la serie real; sin embargo, lo que inquieta es que no es idéntica. Lo ideal sería ver las series superpuestas en una sola curva y obtener de la calibración de un sistema absolutamente óptimo, un EQM igual a cero.

Figura 3.

En este trabajo se muestra un modelo innovador que combina diferentes metodologías y herramientas basadas en el análisis lineal de series de tiempo y la lógica difusa, optimizado por el algoritmo Downhill Simplex Method (Numerical, 1986 - 1992). Los resultados son buenos porque el modelo alcanza a reconstruir una serie muy parecida en la textura, que ya es un logro significativo, pero es indiscutible que es necesario realizar una búsqueda exhaustiva dentro del sistema para identificar los factores que posiblemente afectan la bondad de ajuste en el procesamiento de las series, como en el hecho de que la serie simulada muestra que el modelo sobreestima los valores bajos y subestima los altos (Fig. 3). A partir de los resultados obtenidos es evidente que se pueden conseguir predicciones más precisas si el proceso concentra su mejoramiento en la minimización del EQM (Segura, 2005). Desde ya se prevén metodologías como experimentar con funciones de membresía de formas diferentes, aplicar reglas difusas a la serie del error o aplicar una simulación basada en series de Fourier.

4. REFERENCIAS BIBLIOGRÁFICAS

[1] Altrock, Constantin von. Fuzzy logic and neurofuzzy aplications explained. Englewood Cliffs (New Jersey). Prentice Hall PTR, 1995.        [ Links ]

[2] Bojadziev, George & Bojadziev Maria. Fuzzy sets, fuzzy logic, applications. Advances in Fuzzy Systems Vol. 5, World Scientific. Singapore, 1995.        [ Links ]

[3] Cox, Earl. The Fuzzy Systems handbook. 2nd ed. Cambridge: AP, 1998.        [ Links ]

[4] Instituto de Hidrología, Meteorología y Estudios Ambientales, IDEAM. Datos de las estaciones en la zona de Puerto Salgar. 1960-2004.        [ Links ]

[5] Instituto de Hidrología, Meteorología y Estudios Ambientales, IDEAM. Reportes diarios de los niveles de los ríos en Colombia. www.ideam.gov.co        [ Links ]

[6] Klir, George y Yuan, Bo. Fuzzy sets and fuzzy logic theory and applications. Prentice Hall, EU, Upple Saddle River, New Jersey, 1995.        [ Links ]

[7] Lobbrecht, A.H. & Solomatine, D.P. "Control of water levels in polder areas using neural networks and fuzzy adaptive systems". Published in: Water Industry Systems: vol. 1. Research Studies Press, Ltd. Baldock, UK, 1999, pp. 509-518.        [ Links ]

[8] Maskey, Shreedhar. Uncertainty analysis in flood forecasting and warning system using expert judgement and fuzzy set theory. International Institute for Infrastructural, Hydraulic and Environmental Engineering (IHE). Delft, the Netherlands, 1998.        [ Links ]

[9] MathWorks, The. Fuzzy Logic Toolbox, for use in MATLAB®. The Math Works Inc. June 2004, (Online only).        [ Links ]

[10] Numerical Recipes Software. Numerical Recipes in Fortran 77: The art of scientific computing. Chap. 10.4 Downhill Simplex in Multidimensions. Cambridge University Press, 1986-1992.        [ Links ]

[11] Obregón Neira, Nelson. "Modelo predictivo unidimensional inspirado en teoría del caos y redes neuronales artificiales". En Ingeniería y Universidad, vol.6, No.2, Fundación Cultural Javeriana. Bogotá, julio-diciembre de 2002, pp. 75-92.        [ Links ]

[12] Rivera, Hebert G.; Zamudio H., Eduardo y Pinzón R., Henry. "Modelación hidrológica en tiempo real para soportar las decisiones en el sector de navegación del río Magdalena". En Memorias del XVI Seminario Nacional de Hidrología e Hidráulica, Armenia, Quindío, Colombia, Octubre 29, 30 y 31 de 2004.        [ Links ]

[13] Segura B., J. Alexander. Pronóstico de los niveles del río Magdalena en el sector de Puerto Salgar, Colombia; empleando lógica y conjuntos difusos. Proy. de grado, Ingeniería.Civil. (Dir: Obregón, Nelson) Conv. IDEAM-Fac.Ingeniería. Universidad Nacional de Colombia. Bogotá, 2005.        [ Links ]

[14] Wilches T., Camilo A. Análisis lineal y no lineal en series de tiempo en ingeniería civil. Proyecto de grado, Ingeniería Civil. Facultad de Ingeniería. Universidad de los Andes. Bogotá, 2002.        [ Links ]

BIBLIOGRAFÍA

[15] Dweiri, F.T. y Kablan, M.M. Using fuzzy decisión making for the evaluation of the project management internal efficiency. Article in press. Decision Support Systems, ScienceDirect, 2005, www.elsevier.com/locate/dsw.        [ Links ]

[16] Molano P., Luz. Modelamiento evolutivo en sistemas de lógica difusa. Proyecto de Grado, Ingeniería de Sistemas. Facultad de Ingeniería. Universidad Nacional de Colombia. Bogotá, 2002.        [ Links ]

[17] Williams, Garnett. Chaos Theory Tamed. US Geological Survey. Joseph Henry Press. Washington, D.C, 1997.        [ Links ]