Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.22 Bogotá July/Dec. 2005
Algoritmos de Optimización Combinatoria (AOC) aplicados al diseño de redes de distribución de agua potable
Algorithms of Combinatorial Optimization for the design of water distribution networks
Germán Villalba Fernández de Castro
Investigador, Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Departamento de Ingeniería Civil, Universidad de los Andes.
Juan Guillermo Saldarriaga
Director Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Profesor Titular, Departamento de Ingeniería Civil, Universidad de los Andes.
Recibido 30 de agosto de 2005, aprobado 31 de octubre de 2005.
PALABRAS CLAVE
Diseño, óptimo, redes de distribución.
RESUMEN
Los AOC son metodologías para hallar una aproximación al diseño de costo mínimo de redes de acueducto. Se usa REDES y EPANET para la simulación hidráulica y se resuelven problemas reportados en la literatura, encontrando soluciones de menor costo que cumplen las restricciones hidráulicas. Esta metodología es computacionalmente mucho más rápida que otro tipo de algoritmos usados previamente para solucionar este problema, y se pueden hallar buenas soluciones. Además, es posible optimizar soluciones conocidas para hallar otras de menor costo. Se prueba el problema de la red de Hanoi y se obtienen mejores resultados que los publicados en la literatura.
KEYWORDS
design, water distribution network, hydroinformatic.
ABSTRACT
The ACO are methodologies to find an approximation to least cost design of water distribution network. REDES and EPANET are used for hydraulic simulation and well known problems are solved finding solutions of less cost satisfying pressure constraints. This methodology is computationally much faster when compared with other algorithms used previously to solve this problem and good solution can be found. Furthermore is possible to optimize known solutions to find better solutions. The Hanoi network problem is tested and better solutions were found than those published previously in the literature.
INTRODUCCIÓN
El problema de diseño de redes de distribución de agua potable es bastante complicado debido a la relación no lineal entre el flujo y las pérdidas de cabeza (carga), y a la presencia de variables discretas, como los diámetros de las tuberías comerciales. Adicionalmente, la función de costos de las tuberías también tiene una relación no lineal con los diámetros. De hecho, se ha demostrado que este problema es de complejidad NP-DURO (Yates et al., 1984), lo cual quiere decir que es un problema intratable para el cual no se conoce ningún método determinístico para solucionarlo en un tiempo polinomial.
Teniendo en cuenta lo anterior, el problema de diseñar una red de distribución de agua potable se puede abordar como un problema de optimización combinatoria en donde las variables de decisión son los diámetros de cada una de las tuberías de la red. En esta investigación, se plantea realizar el diseño de redes de distribución de agua potable a través de varios métodos que se pueden usar independiente o conjuntamente para encontrar diseños factibles de bajo costo en un tiempo razonable; los algoritmos propuestos son: Diseño basado en la superficie óptima de presiones, Programación por restricciones y Algoritmos genéticos.
La metodología propuesta consiste en ensamblar un sistema que pueda usar la salida de cada algoritmo para seguir mejorando los resultados, proceso mediante el cual se puede continuar hasta encontrar resultados satisfactorios. El desarrollo de la metodología se implementó originalmente en el programa REDES, desarrollado en el Centro de Investigaciones en Acueductos y Alcantarillados -CIACUA- de la Universidad de Los Andes; los resultados obtenidos se validaron en EPANET (Rossman, 1993).
MARCO TEÓRICO
Para diseñar una red es necesario conocer las coordenadas X, Y y Z de cada uno de los nodos, así como el caudal demandado en cada uno de ellos, la LGH (línea de gradiente hidráulico) de cada una de las fuentes de la red, la conectividad entre los nodos de la red (a través de tubos) y las características físicas de las tuberías.
Diseñar consiste en determinar el diámetro que debe tener cada una de las tuberías de la red, de manera que sea posible llevar el agua desde las fuentes hasta cada nodo manteniendo una presión por encima de la presión mínima permitida. Este problema se ha resuelto tradicionalmente por ensayo y error. Sin embargo, este método no tiene ningún criterio de optimización económica, lo cual lleva a diseños funcionales desde el punto de vista hidráulico pero con unos costos bastante elevados.
El diseño de redes de acueducto se puede modelar como problema de optimización combinatoria en donde las variables de decisión son los diámetros de cada una de las tuberías. El problema consiste en determinar un conjunto de diámetros tal, que se minimice una función de costo (basada en la longitud, diámetro y costo de las tuberías) sujeta a restricciones hidráulicas, comerciales, etc.
RESTRICCIONES HIDRÁULICAS
Se debe cumplir con las siguientes leyes y restricciones:
Ley de Conservación de Masa en cada nodo.
Ley de Conservación de Energía en cada circuito.
La presión en cada nodo debe ser mayor al valor mínimo.
RESTRICCIONES COMERCIALES
Los diámetros solo pueden tomar valores discretos dados por la disponibilidad de diámetros de cada fabricante de tuberías.
RESTRICCIONES ADICIONALES
El método de solución debe ser capaz de encontrar una "buena" solución para una amplia variedad de topologías, demandas en los nodos, topografías, etc.
El método de solución debe ser capaz de encontrar una "buena" solución en un tiempo "razonable" según el tamaño de la red.
ESQUEMA DE SOLUCIÓN
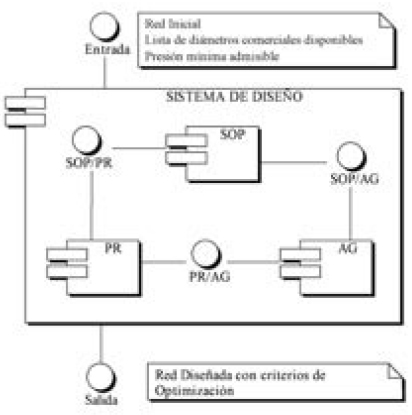
La solución propuesta en esta investigación consiste en hacer uso de los tres métodos descritos a continuación, para resolver el problema del diseño de redes de distribución de agua potable. Se hicieron pruebas empleando cada algoritmo de manera separada, luego de manera cooperativa entre dos algoritmos y, finalmente, el resultado de la integración del sistema en diferentes configuraciones, como se muestra en Figura 1.
Figura 1. Sistema de Diseño de Redes de Distribución de Agua Potable
SUPERFICIE ÓPTIMA DE PRESIONES
Este método consiste en el cálculo de la LGH (LGH ideal) que debería tener cada uno de los nodos de la red para que los diámetros resultantes de las tuberías tengan un costo cercano al mínimo. Este criterio es similar al criterio de Wu (2001) para tuberías en serie, pero aplicado al diseño de redes de distribución de agua potable con cualquier topología. Para calcular esta superficie de LGH, es necesario definir la presión mínima requerida en los nodos y una ecuación que modele la caída de la LGH ideal. Se ha encontrado que, aplicando una ecuación cuadrática, se obtienen mejores resultados debido a que este tipo de función es la que presenta mayor similitud con el criterio de Wu (2001).
Una vez se tiene la LGH objetivo en cada uno de los nodos de la red, se procede a hacer el diseño de cada uno de los tubos como una tubería simple con los caudales obtenidos en una iteración anterior; esto da una mejor aproximación al caudal que debe ir por cada tubería. Este procedimiento se repite hasta que la LGH obtenida sea muy similar a la LGH ideal. Esto daría un diseño casi perfecto si los diámetros fueran continuos, pero en realidad son números discretos y finitos, lo cual hace que se tenga que aproximar el diámetro real a un diámetro comercial.
La aproximación del diámetro se puede hacer al anterior, al siguiente o al más cercano diámetro comercial disponible. En esta investigación se determinó que una buena opción es aproximar al siguiente diámetro comercial para no violar la restricción de presión mínima en los nodos y, posteriormente, disminuir los diámetros mediante un proceso de optimización, basado en un algoritmo de programación por restricciones; aunque también es posible aproximar al anterior diámetro comercial y luego aumentar los diámetros con otro procedimiento de programación por restricciones, luego de lo cual se puede intentar nuevamente el procedimiento de disminución de diámetros.
PROGRAMACIÓN POR RESTRICCIONES (CONSTRAINT PROGRAMMING - CP)
La programación por restricciones es un paradigma para la solución de problemas combinatorios de optimización. Estos problemas combinatorios de optimización se pueden resolver definiéndolos como varias instancias de un problema de satisfacción de restricciones (Contraint Satisfaction Problem - CSP).
Una instancia de un CSP se describe por un conjunto de variables, un conjunto de posibles valores para cada variable y un conjunto de restricciones entre las variables. Al conjunto de los posibles valores de una variable se le denomina el dominio de la variable. Una restricción entre variables expresa las combinaciones de los valores de las variables que están permitidas. Las restricciones pueden ser implícitas (p.e. una fórmula aritmética) o explícitas, en donde cada restricción se expresa como un conjunto de parejas de valores que cumplen la restricción. Un ejemplo de una restricción implícita es el siguiente: "La presión mínima en cada nodo debe ser mayor a 15 mca" (cuando la variable de decisión es el diámetro de la tubería). Un ejemplo de restricción explícita sería: "La tubería X debe tener un diámetro igual a 10 pulgadas".
La pregunta que se desea responder para una instancia de un CSP es si existe una combinación de valores que satisfaga todas las restricciones; a esta combinación se le denomina una solución del CSP. Las restricciones se pueden usar activamente para reducir el esfuerzo computacional necesario para resolver problemas combinatorios y para verificar la validez de la solución, remover valores del dominio de las variables, deducir nuevas restricciones y detectar inconsistencias.
Al aplicar este tipo de algoritmos al diseño de redes de distribución de agua potable, es posible llegar a un buen nivel de optimización, a partir de una solución que ya cumple las restricciones hidráulicas y comerciales, o a partir de una solución que viola ligeramente las restricciones hidráulicas. Por esta razón, funciona muy bien al usarlo en conjunto con un diseño basado en la superficie óptima de presiones.
ALGORITMO GENÉTICO
El algoritmo genético implementado en esta investigación está basado en un algoritmo genético estándar, pero se ha incluido un nuevo operador de mutación que permite transiciones más suaves entre un modelo y otro. Los algoritmos genéticos no incluyen el manejo de restricciones, pero éstas se pueden simular al incluir un término en la ecuación de costo que crece en función de la magnitud de la violación de las restricciones. Esto hace que después de cierto número de iteraciones la gran mayoría de los individuos se mantengan dentro del espacio factible de solución del problema.
Cuando se crea la primera generación de manera aleatoria es muy posible que muchos de los individuos no cumplan con las restricciones. Además, es posible que al combinar dos individuos que sí cumplen con las mismas, sus descendientes no cumplan con las restricciones. En la práctica se han obtenido buenos resultados al simular de esta manera las restricciones del problema, el único inconveniente práctico radica en la gran cantidad de iteraciones necesarias para obtener "buenas" soluciones, aún en problemas relativamente pequeños, lo cual los hace poco prácticos para el diseño de redes de mayor tamaño.
Cuando los algoritmos genéticos se usan en combinación con el diseño basado en la superficie óptima de presiones y un proceso de optimización basado en un algoritmo de programación de restricciones, se obtienen muy buenos resultados en un tiempo de cálculo razonable según el tamaño del problema.
ALGORITMO DE OPTIMIZACIÓN COMBINATORIO
Con el fin de facilitar el proceso de diseño se establece un orden que permite una buena calidad de resultados en un número muy pequeño de simulaciones. El algoritmo combinatorio definitivo, utilizado en esta investigación, se define como la siguiente secuencia de ejecución:
Se realiza el prediseño de la red con el método basado en la determinación de la Superficie Óptima de Presiones y después se aplica un algoritmo de Programación por Restricciones, el cual garantiza que la solución obtenida cumpla con todas las restricciones del problema. Finalmente, se aplica un segundo algoritmo de Programación por Restricciones para disminuir los diámetros hasta que no se pueda disminuir un solo diámetro sin violar las restricciones hidráulicas; esto da una excelente solución en un tiempo muy corto.
EJEMPLO RED DE HANOI
El siguiente ejemplo ha sido tratado por varios autores y se incluye con el propósito de comparar los resultados con los obtenidos en otras investigaciones. La implementación de la solución se realizó originalmente en el programa REDES y se validó con EPANET para poder hacer una comparación objetiva con los resultados obtenidos por otros autores.
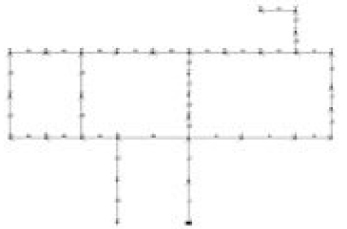
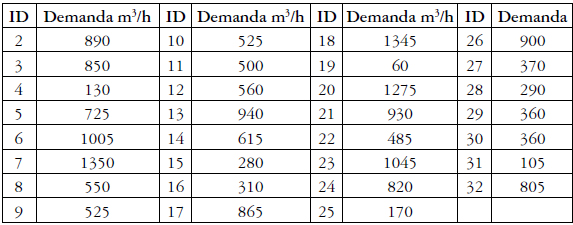
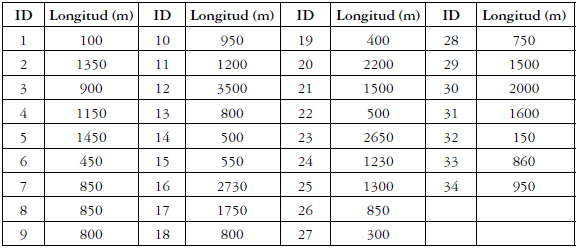
La red de Hanoi fue presentada por primera vez por Fujiwara y Khang (1990). Es una red con una sola fuente; está compuesta por 3 circuitos básicos, 31 nodos, un embalse y 34 tubos. Todos los nodos se encuentran a la misma elevación y no hay pérdidas menores en las tuberías. En este ejemplo para el cálculo de las pérdidas por fricción se usa la ecuación de Hazen-Williams con un coeficiente Chw=130 para todas las tuberías de la red. La LGH de la fuente es de 100 mca y la presión mínima requerida es de 30 mca. La Figura 2, la Tabla 1 y la Tabla 2 muestran la información necesaria para reproducir este ejemplo.
Figura 2. Red de Hanoi
Tabla 1. Demandas en los nodos de la red de Hanoi
Tabla 2. Longitudes de las tuberías de la red de Hanoi
El conjunto de diámetros comerciales y sus correspondientes costos por unidad de longitud se muestran en la Tabla 3. El tamaño del espacio de búsqueda es 634 (aproximadamente 2.86x1026). La mejor solución reportada en la literatura tiene un costo de $6.182 millones, encontrada por el algoritmo genético rápido desordenado (fmGA - fast messy genetic algorithm) en 113626 simulaciones (Wu, 1975). Algunos autores han encontrado soluciones más baratas [2, 8, 10], pero al hacer una simulación hidráulica de estos modelos en EPANET se obtienen presiones por debajo de 30 mca.
Tabla 3. Diámetros comerciales y costos para la red de Hanoi
Durante el desarrollo de este problema se encontraron varias alternativas de solución, algunas de las cuales tienen un costo inferior al mejor reportado en la literatura. La Tabla 4 muestra algunas soluciones obtenidas con los costos y el número de iteraciones necesarias. Cada nueva solución se halla a partir de la solución anterior, lo cual permite seguir mejorando los resultados, aunque en cada iteración la solución mejora en menor magnitud y la diferencia del costo es menor; al parecer el método de solución se acerca cada vez más al mínimo global. Cabe destacar que a pesar del gran número de simulaciones que se requieren para encontrar las soluciones de costo mínimo, la simplicidad de los algoritmos empleados hace que el tiempo de cálculo, en términos computacionales, sea muy corto.
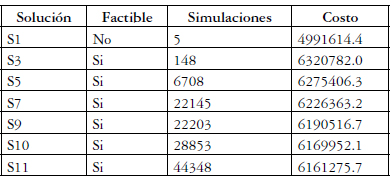
Tabla 4. Soluciones obtenidas en el ejemplo de la red de Hanoi
En la Tabla 4 se puede ver que la solución S3 es relativamente buena y solo se necesitaron 148 simulaciones hidráulicas. Es importante notar que se encontraron 2 soluciones con un costo inferior a US $6.182 millones (S10 con US $6.170 millones y S11 con US $6.161 millones), además se necesitó un menor número de iteraciones (S10 con 28853 y S11 con 44348). La Tabla 5 muestra una comparación entre varias soluciones halladas por diferentes autores:
Tabla 5. Comparación de las soluciones al problema de la red de Hanoi
En la Tabla 5 "Factible" significa que al hacer la simulación hidráulica con EPANET las presiones en los nodos son superiores a 30 mca. Esta tabla muestra que durante esta investigación se obtuvieron 3 nuevas soluciones menores a US$6.182 millones (la mejor solución previamente reportada en la literatura).
El método de solución da muy buenos resultados; además, es posible encontrar nuevas soluciones a partir de otras existentes. La solución "AOC (C&S) 2004" se obtuvo al aplicar el AOC a la solución publicada por Cunha y Sousa (1999). En algún momento se consideró ésta como la mejor solución, pero después se determinó que al correrla con EPANET se obtienen soluciones con presiones por debajo de 30 mca; sin embargo, al introducir este modelo en el AOC se obtiene una solución de menor costo que las publicadas anteriormente (Tabla 5).
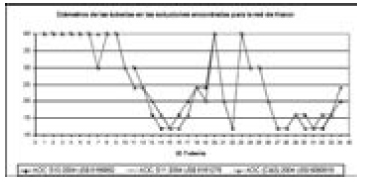
Figura 3. Diámetros de las tuberías en las soluciones econtradas para la red de Hanoi
CONCLUSIONES
Con la metodología propuesta se llega a una buena aproximación para superar el problema de diseño de redes de distribución de agua potable de costo mínimo.
La aplicación de un algoritmo basado en la Superficie Óptima de Presiones se puede ver como una heurística que orienta la solución del problema de diseño de redes de distribución de agua potable. La solución obtenida no respeta las restricciones comerciales de disponibilidad de diámetros, pero al usarse en conjunto con un método de optimización basado en Programación por Restricciones se puede llegar a buenas soluciones en un número de iteraciones menor a los reportados en la literatura. Además, es posible combinar esta solución con otros métodos de optimización como los algoritmos genéticos o muchos otros disponibles en la literatura universal (Glover y Kochenberg, 2003)
Es posible desarrollar un sistema que acople varios módulos de optimización independientes como una línea de producción, en donde cada investigador puede elegir el orden en el que se ensambla dicho sistema. Este enfoque permite el desarrollo de múltiples métodos de optimización, como los que están disponibles en la literatura.
En esta investigación se han encontrado varias soluciones más económicas que las reportadas en la literatura para el problema del diseño de la red de Hanoi, algunas de las cuales se han encontrado usando únicamente los métodos desarrollados en esta investigación. Sin embargo, es posible ingresar soluciones encontradas en otras investigaciones (Ver Cunha y Sousa, 1999, y Savic y Walters, 1995) y encontrar mejores soluciones que cumplen con todas las restricciones del problema.
El AOC (Algoritmo de Optimización Combinatoria) que finalmente se propone en esta investigación incluye el uso de dos esquemas de solución, la Superficie Óptima de Presiones y la Programación por Restricciones. Éste permite el diseño de redes de distribución de agua potable incluyendo criterios de optimización, los cuales se pueden modificar para incluir costos asociados a las fugas de agua en la red y parámetros de calidad del agua. El AOC hace factible el diseño optimizado de redes de distribución de redes relativamente grandes, ya que se llegan a buenas soluciones con un pequeño número de simulaciones hidráulicas.
REFERENCIAS
[1] Baptiste, P.; Le Pape, C. y Nuijten, W. Constraint-based scheduling: applying constraint programming to scheduling problems, 2001. [ Links ]
[2] Cunha, M. y Sousa, J. "Water Distribution network design optimization: Simulated annealing aproach". En Journal of Water Resources Planning and Management, Vol. 125, No 4, July/August 1999. ASCE. [ Links ]
[3] Fujiwara, O. y Khang D.B. "A two-phase decomposition method for optimal design of looped water distribution networks". En Water Res. Research, 26(4), 1990, pp. 559-5549. [ Links ]
[4] Glover, F y Kochenberger G.A. Handbook of Metaheuristics. Operations Research Management Science. Kluver Academic Publishers, 2003. [ Links ]
[5] Liong, S. y Atiquzzaman, M. "Optimal Design of Water Distribution Network using Shuffled Complex Evolution". En Journal of The Institution of Engineers. Singapore.:Vol. 44 Issue 1. 2004. [ Links ]
[6] Prasad, T.D. y Park, N. "Multiobjetive Genetic Algorithm for Design of Water Distribution Networks". En Journal of Water Resources Planning and Management, Vol. 130, No 1, January 1, 2004. ASCE. [ Links ]
[7] Rossman, L.A. EPANET, Users Manual. Risk Reduction Engineering Laboratory, U.S. Environmental Protection Agency, Cincinnati, Ohio, 1993. [ Links ]
[8] Savic, D.A. y Walters, G.A. Genetic operators and constraint handling for pipe network optimization, 1995. [ Links ]
[9] Wu, I. "Design of Drip irrigation Lines". Journal of the irrigation and Drainage Division, Vol. 101, No IR4, December 1975. ASCE. [ Links ]
[10] Wu, Z.Y.; Boulos, P.F.; Orr C.H. y Ro, J.J. "Using genetic algorithms to rehabilitate distribution system", En Journal for American Water Works Association, November 2001, pp.74 - 85. [ Links ]
[11] Yates, D.F.; Templeman, A.B. y Boffey T.B. "The computational complexity of the problem of determining least capital cost designs for water supply networks". Engg. Optimization, 7(2), 1984, pp.142-155. [ Links ]