Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.22 Bogotá July/Dec. 2005
Optimización operacional de redes de distribución de agua potable con el fin de maximizar la uniformidad de presiones en los nodos de consumo
Operational optimization of drinking water distribution networks in order to maximize the uniformity of pressure in the consumer nodes
Diego Alejandro Araque Fuentes
Ingeniero Civil. Investigador Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA. Universidad de los Andes,
Juan Guillermo Saldarriaga
Ingeniero Civil, MSc Ingeniería Hidráulica. Profesor Titular Departamento de Ingeniería Civil y Ambiental, Director del Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Universidad de los Andes.
Recibido 9 de septiembre de 2005, aprobado 30 de octubre de 2005.
PALABRAS CLAVES
Índice de Resiliencia, optimización de redes de distribución de agua; rehabilitación de tuberías.
RESUMEN
En el presente trabajo se muestra que con el desarrollo de un algoritmo determinístico se logra uniformizar el estado de presiones de servicio en una red de distribución de agua potable. Para lograr esto de forma óptima, se debe maximizar un Índice que relaciona la potencia por unidad de peso disipada por la red y disponible para disipar por la misma (Índice de Resiliencia [2]), lo cual mejora la habilidad del sistema de distribución para enfrentar eventuales fallas en el mismo, retarda los procesos de renovación de tuberías y minimiza el nivel de fugas en la red.
KEYWORDS
Resilience Index, Water Distribution Networks Optimization; Pipe Rehabilitation.
ABSTRACT
The present paper will show that throughout the development of a deterministic algorithm the uniformity of the pressure service level in the Water Distribution Network (WDN) can be maximized. To obtain this in an optimal way, one must maximize an Index that relates the power by unit of weight dissipated by the network and the power by unit of weight available to dissipate by the same one (Resilience Index [2]), it improves the ability of the WDN to cope with possible failures in the system, slows down the pipes renovation processes and diminishes the level of leaks in the network.
1. INTRODUCCIÓN
El mantenimiento de redes de distribución de agua potable consiste típicamente en la rehabilitación, reparación y renovación del sistema de tuberías que lo componen. La mayoría de las políticas de mantenimiento combinan el desarrollo de la técnica de soporte de decisión a partir del reemplazo de líneas de tubería adecuadas, basadas en el juicio técnico bajo el buen conocimiento hidráulico del sistema. A continuación se presentará una metodología para lograr la óptima operación de redes existentes de distribución de agua potable, con el objetivo de maximizar el estado de presiones en los nodos de consumo de la misma.
2. INDICADORES DE COMPORTAMIENTO PARA LA OPTIMIZACIÓN DE REDES DE ACUEDUCTO, CON EL FIN DE UNIFORMIZAR EL ESTADO DE PRESIONES
En ingeniería, el comportamiento de cualquier sistema en términos de sus cargas y la resistencia puede analizarse de la siguiente manera: Si X = (X1, X2,…, Xn) es el vector de las variables aleatorias que influencian la carga (L) y/o la resistencia (R) del sistema, la función de comportamiento, G(X), se define como sigue (ver Ecuación 1).
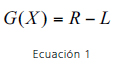
La superficie de falla (estado límite), donde G = 0, separa todas las combinaciones de X existentes en el dominio de falla de las presentes en el dominio de supervivencia.
El nivel de confiabilidad en el nodo i de la red de distribución de agua potable es evaluado de la siguiente manera (ver Ecuación 2).
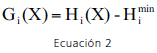
donde Hi(X) es la presión modelada en el nodo i como función del vector de la capacidad hidráulica en las tuberías, X, y Himin es la presión mínima permitida en el nodo i. Por lo tanto, para evaluar la confiabilidad en cada uno de los nodos de la red de distribución, se debe especificar la función de comportamiento para cada nodo y, mediante el seguimiento de una metodología, encontrar las combinaciones existentes en el dominio de supervivencia.
A partir de la definición de confiabilidad en el nodo i de la red de distribución, es necesario plantear una medida de confiabilidad para todo el sistema de distribución. Lo que se busca con la metodología de optimización de redes de acueducto, con el fin de uniformizar el estado de presiones, es minimizar la función de comportamiento en cada nodo de la red de distribución (ver Ecuación 3).
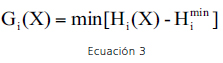
Lo anterior, como se verá más adelante, se logra al maximizar el Índice de Resiliencia (Ii) y el Coeficiente de Uniformidad (CU) al mismo tiempo que se minimiza la Desviación Estándar (DESV) del estado de presiones en los nodos de consumo.
1.1. ÍNDICE DE RESILIENCIA
Las pérdidas internas de presión disminuyen la confiabilidad del sistema. El incremento en las pérdidas durante las condiciones de falla puede ser conocido si la potencia disponible para ser disipada por el sistema excede la que realmente disipa el mismo. Basado en esta premisa, se define el índice de resiliencia. Todini (2000) propuso el siguiente índice de resiliencia (Ii), basado en el concepto que la potencia de entrada en una red es igual a la potencia perdida internamente por el sistema ocasionada por los efectos de la fricción más la potencia entregada en los nodos de demanda (ver Ecuación 4).
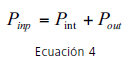
La potencia total de entrada incluye la potencia suministrada por una bomba más la suministrada por los embalses (ver Ecuación 5).
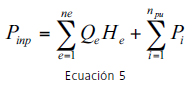
donde Qe y He son el caudal y la cabeza de entrada; ne: número de embalses; Pj: potencia por unidad de peso suministrada por la bomba i; npu: número de bombas en la red. La potencia total de salida está dada por la Ecuación 6:
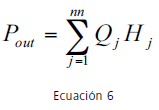
donde Qj: demanda en el nodo j; Hj: es la presión con la cual se satisface la demanda Qj; y nn: es el número de nodos de toda la red. Por lo tanto, el índice de resiliencia de la red se define en la Ecuación 7.
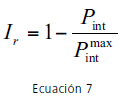
donde Pint: es la potencia disipada por la red; y max Pint: máxima potencia que puede ser disipada internamente por la red para garantizar la demanda Q y la presión mínima H* requerida en cada uno de los nodos. Al sustituir los valores apropiados se encuentra la ecuación para el índice de resiliencia (Ecuación 8).
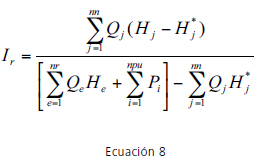
1.2. UNIFORMIDAD DE PRESIONES
Al maximizar el Índice de Resiliencia, que representa la relación entre la energía disipada por el sistema actual con una configuración dada respecto a la energía óptima disipada, se logra uniformizar el estado de presiones. La definición de energía óptima disipada hace referencia a qué tanta energía se espera que el sistema de distribución de agua potable disipe en cada uno de los tubos que la conforman.
El índice utilizado para analizar el grado de uniformidad del estado de presiones en la red es el coeficiente de uniformidad (CU en la Ecuación 9), el cual relaciona la presión sobre todos los nodos con la máxima presión de entrega encontrada.
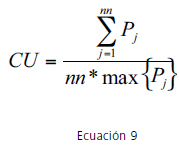
donde Pj es la presión de servicio en el nodo j.
1.3. DESVIACIÓN ESTÁNDAR
La desviación es una medida estadística de las diferencias entre un conjunto de valores con el promedio del mismo. Estas diferencias pueden ser positivas, cuando el valor se encuentra por encima del promedio, y negativas, cuando el valor se encuentra por debajo del promedio. Por lo tanto, el procedimiento a desarrollar debe garantizar que en ningún momento se encuentren valores por debajo de la presión mínima de entrega permitida, en este caso H* (ver Ecuación 10).
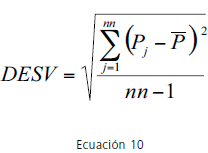
donde P es la presión promedio en la red de distribución de agua potable.
1.4. PERJUICIO HIDRÁULICO
El perjuicio hidráulico es una medida relativa del índice de resiliencia para cada una de las configuraciones de tuberías encontradas, el cual indica que la optimización del proceso de una a otra configuración va siendo cada vez menor a medida que se maximiza la conservación de energía. El perjuicio hidráulico se calcula a partir de la Ecuación 11.

donde k representa el número de cambios realizados durante el proceso. Cada cambio realizado en la red de distribución representa la modificación en el diámetro de una de las tuberías encontradas a partir de la aplicación de la metodología.
3. SOPORTE DE DECISIÓN PARA LA OPTIMIZACIÓN DE REDES DE ACUEDUCTO CON EL FIN DE UNIFORMIZAR EL ESTADO DE PRESIONES
El problema se resuelve a partir de la implementación de un algoritmo determinístico que debe escoger las tuberías en las cuales se debe modificar su diámetro, para lograr maximizar la uniformidad de presiones en la red. Cada modificación en el diámetro de la tubería escogida corresponde a aumentarlo al siguiente comercial, siguiendo un rango de diámetros comerciales definido previamente por el usuario, a partir del diámetro actual que tenga la tubería. Para escoger la tubería en la cual se debe realizar la modificación, se tienen todas las tuberías de la red y las posibles modificaciones en los diámetros de las misma (espacio solución), entre los cuales se encuentran aquellas tuberías que maximizan la uniformidad de presiones (optimizan el proceso) al realizar la modificación en el diámetro respectiva.
El algoritmo determinístico se desarrolla paso a paso: al inicio se tienen dos conjuntos, uno de tuberías escogidas con las modificaciones consideradas en los diámetros, y el de tuberías no escogidas con las posibles modificaciones consideradas, los cuales se encuentran vacíos. En cada paso se adiciona la tubería, con la respectiva modificación, que maximice la uniformidad de presiones al primer conjunto y se van encontrando aquellas que no solucionan de manera óptima el problema, las cuales pasan al segundo conjunto.
El proceso de identificación de la tubería que debe escogerse y la respectiva modificación considerada en su diámetro, involucra la implementación de tres funciones: la función de selección no objetiva, la función de factibilidad, y la función de selección objetiva. Al final se tiene un conjunto de tuberías escogidas, en las cuales se deben realizar ciertas modificaciones en sus diámetros para alcanzar cierto nivel de uniformidad de presiones. Estas tuberías conforman la solución al problema de maximizar la uniformidad de presiones en la red.
1.1. FUNCIÓN DE SELECCIÓN NO OBJETIVA
La función de selección no objetiva, como su nombre lo indica, escoge dentro de todas las tuberías de la red a la tubería en la cual su modificación en el diámetro maximice el índice de resiliencia de una configuración de tuberías a otra; es decir, a la tubería que al aumentar su diámetro al siguiente comercial genere el mayor Ir de todas las posibles modificaciones evaluadas. Sin embargo, esta función no tiene en cuenta el nivel de uniformidad de presiones y el rango de presiones encontrado con la modificación considerada, lo cual es el objetivo final de la implementación de la metodología.
1.2. FUNCIÓN DE FACTIBILIDAD
Por razones técnicas y normativas se han establecido reglas para el diseño de redes de distribución. La función de factibilidad es una función de castigo, la cual verifica que el aumento considerado en el diámetro de la tubería escogida en cada una de las configuraciones encontradas no supere el diámetro máximo establecido por la norma técnica de diseño. Sin embargo, esta función no tiene en cuenta la optimización del proceso.
1.3. FUNCIÓN DE SELECCIÓN OBJETIVA
El objetivo que se busca con el procedimiento es el de uniformizar el estado de presiones en toda la red de distribución. Esto se logra maximizando el índice de resiliencia, al encontrar que la energía disipada por el sistema sea igual a la energía disponible para disipar. Las tuberías escogidas, con sus respectivas modificaciones, deben garantizar lo siguiente en cada una de las configuraciones encontradas:
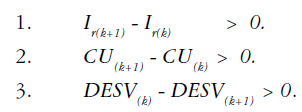
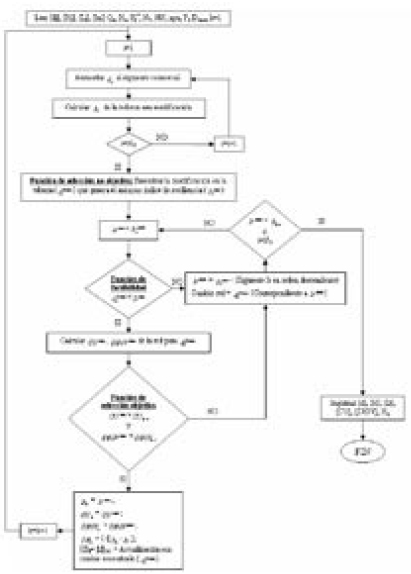
Siendo los subíndices k y k+1 las configuraciones anterior y siguiente respectivamente, encontradas durante el desarrollo del proceso. La estructura del soporte de decisión es el algoritmo determinístico mostrado en la Figura 1.
Figura 1. Estructura del algoritmo determinístico implementado
4. DESARROLLO DEL ALGORITMO
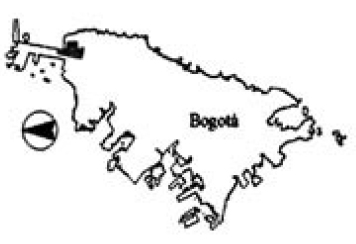
En el presente artículo, se analizó el Sector 35 del sistema de distribución de agua potable de la ciudad de Bogotá D.C.; el cual se encuentra limitado al norte por la Calle 200, al sur por la Calle 170, al oriente por la Avenida 9 y al occidente por la Autopista Norte. La localización del Sector 35 se muestra en la Figura 2 y la configuración de tuberías en la Figura 3. El análisis realizado corresponde a un análisis estático del estado de presiones en la red. Esto se debe a que se modelaron los consumos de forma constante en los nodos, respecto al tiempo.
Figura 2. Ubicación del Sector 35 en la red matriz de Bogotá D.C.
Figura 3. Distribución de tuberías de la red del Sector 35
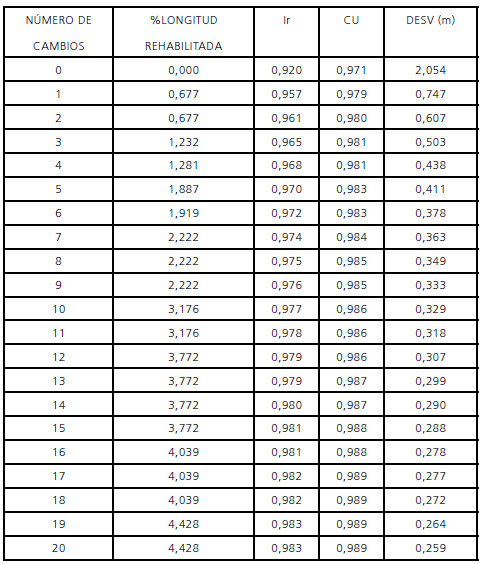
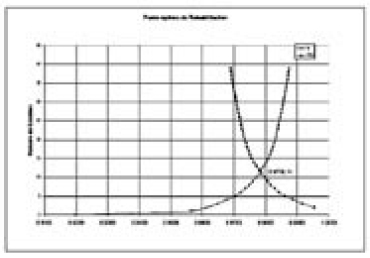
La evolución de los índices se presenta en la Tabla 1 y el proceso de maximización del Índice de Resiliencia y el efecto sobre el Coeficiente de Uniformidad se puede observar en la Figura 4 y en la Figura 5 respectivamente. El punto óptimo de rehabilitación corresponde a realizar 11 modificaciones en los diámetros de las tuberías de la red. El Índice de Resiliencia tiene un comportamiento asintótico respecto a la rehabilitación de la red de distribución en el ejemplo de aplicación. El valor teórico del Índice de Resiliencia puede variar entre 0 y 1. Sin embargo, para sistemas reales de distribución, este valor nunca llega a ser 1.
Tabla 1. Evolución de la aplicación de la metodología a la red del sector 35.
Figura 4. Evolución el Índice de Resilencia y ubicación del punto óptimo de rehabilitación
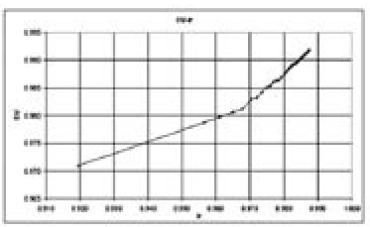
Figura 5. Relación entre la Uniformidad de Presiones y el Índice de Resilencia
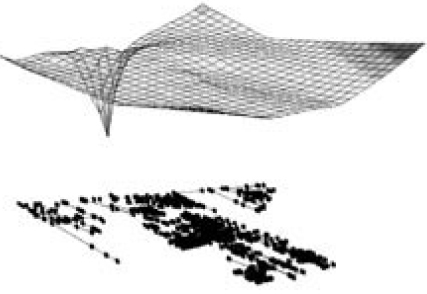
El plano inicial de presiones y el plano en el punto óptimo de rehabilitación, luego de aplicar la metodología, se muestran en la Figura 6 y en la Figura 7 respectivamente.
Figura 6. Plano inicial de presiones de la red del Sector 35
Figura 7. Plano óptimo de presiones de la red del Sector 35
En la Figura 6 se observa una inclinación más pronunciada de este plano inicial de presiones; mientras que en la Figura 7, correspondiente al punto óptimo de rehabilitación, el plano de presiones es más uniforme. Con esto se logra disminuir el riesgo hidráulico que representa un plano irregular de presiones, el cual motiva la presencia de fugas de agua debido a la presencia de zonas con altas presiones. Estas zonas son necesarias para transportar el agua a las zonas con presiones mínimas requeridas.
La principal diferencia física entre los planos de presiones presentados, radica en el hecho que la desviación de presiones antes de la aplicación de la metodología corresponde a un valor de 2.05 metros y en el punto óptimo de rehabilitación a un valor de 0.31 metros; lo cual corresponde a una disminución en la Desviación Estándar del estado de presiones del 84.52%, lograda a partir de la rehabilitación del 3.17% de la longitud total de tubería en el Sector 35. Además, se logra un aumento en el Coeficiente de Uniformidad del 1.57% y un aumento del 6.337% en la conservación de la energía en la red.
5. CONCLUSIONES
6. REFERENCIAS BIBLIOGRÁFICAS
[1] Gilles Brassard, Paul Bratley. Fundamentals of algorithmics. Second Edition. Prentice-Hall, 1998. [ Links ]
[2] Saldarriaga, Juan G. Hidráulica de tuberías. 1a Edición. Editorial Mc Graw Hill, 1998. [ Links ]
[3] Todini E. "Multiobjective Genetic Algorithms for Design of Water Distribution Networks". En Journal of Water resources Planning and Management, vol. 130 No.1. ASCE, 2004, pp. 73-82. [ Links ]