Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista de Ingeniería
versão impressa ISSN 0121-4993
rev.ing. n.23 Bogotá jan./jun. 2006
Clasificación y detección de fallas en Sistemas Dinámicos
Classification and detection of fails in Dynamic Systems
Javier Hernando Pardo Mayorga
Ingeniero Electrónico. Magíster en Ingeniería Electrónica y Computadores. Universidad de los Andes.
Alain Gauthier Sellier PhD.
Decano Facultad de Ingeniería. Universidad de los Andes
Recibido 8 de marzo de 2006, aprobado 7 de mayo de 2006.
PALABRAS CLAVE
Análisis de Componentes Principales, Desigualdades Lineales Matriciales, método LAMDA de clasificación, Observadores adaptivos.
RESUMEN
En los sistemas dinámicos se pueden presentar fallas en cualquier instante de tiempo, estas fallas pueden ser generadas en gran cantidad de casos por la variación de uno o más parámetros de la planta o del sistema dinámico. En este trabajo se propone la detección de fallas en una planta no lineal de dos tanques acoplados uno con área constante y otro variable con la altura esto basado en observadores adaptivos, sustentado con clasificación LAMDA y análisis de componentes principales. Se presenta la aplicación del algoritmo en un sistema no lineal, control del nivel en un sistema de tanques acoplados, así como el análisis de resultados conclusiones y perspectivas futuras.
KEYWORDS
Principal Components Analysis, Linear Matrix inequalities, LAMDA Classification Method, Adaptive Observers.
ABSTRACT
In the dynamic systems a fail can occur in any moment, the fail can be present for variations in one or more parameter of the dynamic system. This paper present a fail detection in a non linear system compose by two tanks in parallel one with constant transversal area and the other one with variable area, the work is develop with adaptive observers and LAMDA classification. The application on this paper is in a non linear system, the level control in the two tank system.
I. INTRODUCCION
En la actualidad la operación de procesos industriales no sólo está basada en su controlabilidad, también en la supervisión y detección de fallas para de este modo aumentar la confiabilidad, seguridad y disminuir costos. La integración de detección de fallos con diagnostico y controladores en los procesos industriales pueden ser de gran utilidad para la industria.
Detección de fallas y aislamiento (FDI, por sus siglas en ingles) basado en observadores adaptivos se presenta como alternativa para la determinación de los fallos que se dan en un proceso durante su operación, o en presencia de degradaciones de los componentes del sistema lo que conlleva a variaciones lentas de los parámetros, esto como ayuda para establecer las acciones correctivas y de mantenimiento necesarias.
El uso de los observadores adaptivos en la determinación de fallas en los sistemas dinámicos es una herramienta válida para modelos por representación de estados, en los casos en los que existen variables que no son medibles el problema de la estimación es un poco más compleja pero viable. En este trabajo se propone la utilización de un observador adaptivo por cada uno de los parámetros a estimar, con la ayuda de Análisis de componentes principales (ACP) que es un análisis estadístico que permite la transformación de datos multivariados a un espacio de menos dimensiones sin mayor pérdida de generalidad para disminuir la cantidad de datos a clasificar, la cual se llevará a cabo con la metodología LAMDA (Learning Algorithm for Multivariable Data Analysis), que es un método de clasificación difusa basada en el grado de adecuación de un elemento a una clase, que se puede comparar con el grado de pertenencia de un objeto a un conjunto difuso.
En la segunda parte se expone la demostración matemática con la que se fundamentan los observadores adaptivos. En la tercera parte se mostrarán algunos detalles de la clasificación LAMDA. En la cuarta sección se darán las principales características del análisis de componentes principales. En la quinta parte se trataran el sistema dinámico donde se aplicaron las metodologías. La sexta mostrara los resultados obtenidos. La séptima parte tratará las conclusiones.
II. DETECCIÓN DE FALLAS Y AISLAMIENTO (FDI)
El método es basado en observadores adaptivos para la detección y diagnostico de fallas en sistemas no lineales. Los cuales podrán determinar la variación de uno o más parámetros [1].
A. Sea el sistema
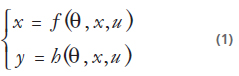
Donde x, y y u son respectivamente los estados, las salidas y las entradas del sistema, f, h son funciones no lineales de x y u caracterizadas por los parámetros q sujetos a variaciones.
B. Modelamiento de fallas
FDI permite el modelamiento de fallas basado en variaciones de parámetros en el sistema (1) o como parámetros aditivos; en este trabajo se presentarán los dos posibles tipos de fallos.
Los fallos están determinados por variaciones de uno o más parámetros, se asume q0 como valores nominales de los parámetros caracterizando así al sistema libre de fallos. Por lo tanto se puede decir que existe una falla cuando hay una desviación en los valores de los parámetros q0, de esta forma el método presentado en este paper puede determinar la presencia de fallas en uno o más parámetros.
C. Observadores para sistemas no lineales
Dado el sistema en la forma (1), el observador es estimador del estado x(t) para observaciones en u(t) y y(t). Entonces el observador es de la forma:
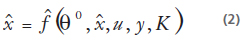
Donde es la estimación de x, 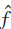 es una función no lineal y K es el vector de sintonización de los parámetros q.
es una función no lineal y K es el vector de sintonización de los parámetros q.
D. Observadores adaptivos
En la presencia de cambios o cuando algunos parámetros de los sistemas no son conocidos, los observadores clásicos no son los mejores para la estimación de estados: los observadores adaptivos pueden ser usados para estimación de estados al mismo tiempo que para estimar los parámetros desconocidos, suponiendo que los parámetros q no son conocidos o son sujetos a cambios, el observador es de la forma:
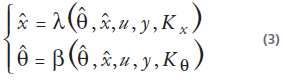
Donde 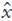 y
y 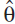 la estimación de x y q respectivamente, l y b son funciones no lineales y Kx y Kq son las ganancias sintonización.
la estimación de x y q respectivamente, l y b son funciones no lineales y Kx y Kq son las ganancias sintonización.
Es claro que un observador adaptivo puede ser usado tanto para la identificación como la estimación de los parámetros q en variaciones lentas.
Es más práctica la estimación de un solo parámetro más el estado por observador que varios parámetros más el estado.
Luego de haber determinado la sensibilidad de la predicción del error con un observador ordinario, se puede proceder a estimar los parámetros susceptibles a variaciones con su correspondiente constante de sensibilidad.
De acuerdo a esto se tendrán n+1 observadores, un observador ordinario y n observadores adaptivos correspondientes a cada uno de los parámetros susceptibles a variaciones.
E. Diseño de observadores adaptivos, basado en observadores de alta ganancia
Teniendo en cuenta el sistema en (1), asumiendo que x Î Rn y y Î R luego de cambios en las variables de estado, se tiene la forma triangular:
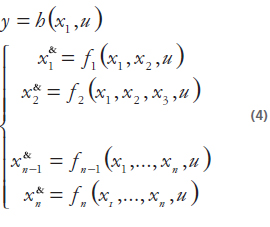
Donde 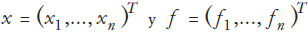 ,
,
definiendo:
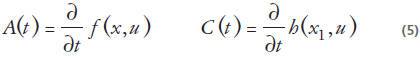
Entonces existe una matriz simétrica definida positiva S tal que 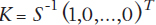 satisface:
satisface:
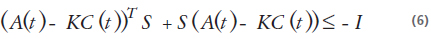
y el observador:
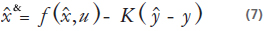
Tiene convergencia exponencial, para cualquier condición inicial 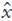 (0). (Para más detalles {1}{2}{3}{6}{7})
(0). (Para más detalles {1}{2}{3}{6}{7})
F. Generación de residuos
La operación sin fallos es caracterizada por el vector de valores nominales q0 el cual es conocido, sean los residuos definidos como la correspondiente predicción del error:
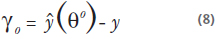
Sabiendo que para cada parámetro a estimar se tiene un observador y definido de la misma forma su correspondiente residuo es:
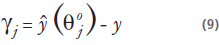
III. METODOLOGÍA DE CLASIFICACIÓN LAMDA
LAMDA, algoritmo de clasificación difusa, permite clasificación cualitativa y cuantitativa, y analiza el grado de adecuación del elemento a cada clase.
MADi (Marginal Adequacy Degree) Grado de adecuación marginal, éste corresponde a cuanto contribuye el i-ésimo atributo a la clase m. MAD es un vector que muestra la ubicación del elemento con respecto a la clase m.
MAD con atributos cuantitativos.
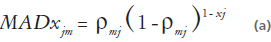
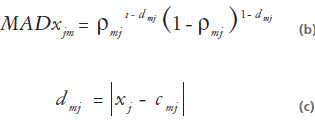
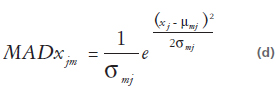
xj es el valor presente en el descriptor j, para el individuo x. rmj ñ es el valor medio de los xj y cmj la mediana de los mj que pertenecen a la clase j.
GADm (Global Adequacy Degree) Grado de adecuación global, se combinan los grados de adecuación marginal (MAD) mediante operaciones difusas.
Para cada elemento que se va a clasificar se determina el grado de adecuación marginal (GAD) de cada descriptor del individuo, respecto al descriptor de cada clase. [4] [5].
IV. ANÁLISIS DE COMPONENTES PRINCIPALES
Análisis de componentes principales es un análisis estadístico que permite la transformación de datos multivariados a un espacio de menos dimensiones sin mayor pérdida de generalidad, donde los nuevos componentes son una combinación lineal de las variables originales con la característica adicional que ahora éstos son independientes.
En la interpretación de los resultados es importante el conocimiento que posea el experto sobre el proceso dado el análisis de magnitud y signo de las correlaciones de las variables iniciales.
El análisis de componentes principales se presenta de manera útil para la disminución de los datos que entrarán en la clasificación y de este modo poder disminuir los tiempos en el proceso y muy especialmente al realizarlo en tiempo real.
V. SISTEMA DE TANQUES ACOPLADOS
El sistema dinámico a analizar consiste en dos tanques acoplados, uno con área transversal constante y otro cuya área varía dependiendo de la altura, este tanque adiciona no linealidades en el sistema.
El sistema corresponde a dos tanques, una bomba que alimenta al sistema con agua, una salida en el tanque de área variable dependiendo de la altura. Adicional a esta composición, dos válvulas en cada uno de los tanques que simulan fugas en el sistema, estas fugas serán las fallas que se pueden presentar y con las que se desarrollara la metodología propuesta.
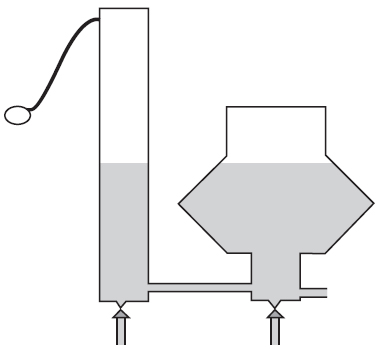
Ilustración 1. Diagrama de los tanques acoplados
Las ecuaciones que modelan el sistema se presentan a continuación:
Área Tanque Lineal
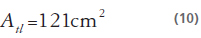
Área Tanque no Lineal
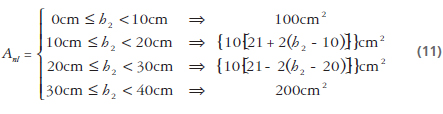
A. Ecuaciones de la dinámica del sistema
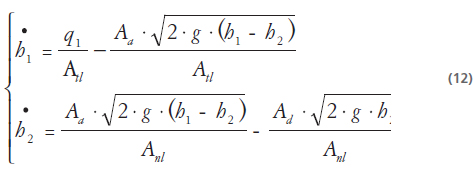
B. Sistema más fallas
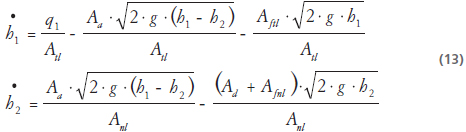
Nótese que en la primera ecuación de estado la falla es aditiva y en la segunda se puede modelar como la variación de un parámetro.
Sea el observador ordinario:
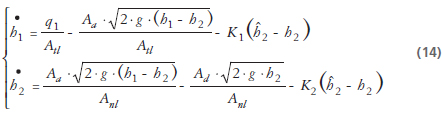
Y los observadores adaptativos:
Observador 1
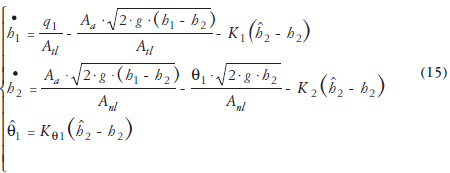
Observador 2
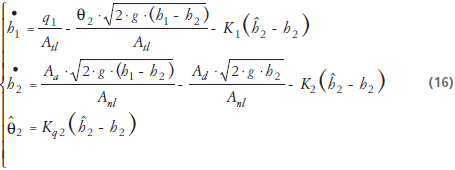
Y los residuos:
Observador ordinario
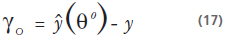
Y de los observadores adaptativos:
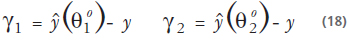
VI. ANÁLISIS DE RESULTADOS
Los resultados están basados en la clasificación con la metodología LAMDA de los residuos generados por los observadores adaptivos y el observador ordinario dado el nivel de referencia y en presencia de fallas, posterior al análisis de componentes principales para realizar la reducción de variables a ser analizadas.
Sean los valores de las constantes del sistema dinámico de la ecuación 14:
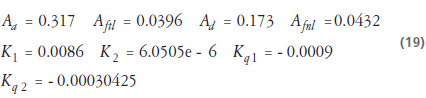
Teniendo en cuenta el cálculo del MAD a utilizar: MAD con atributos cuantitativos:
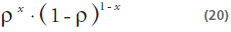
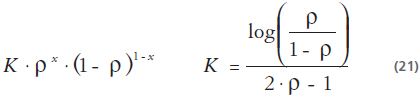
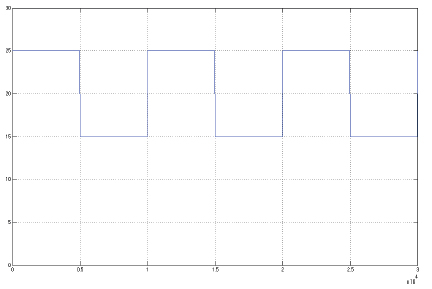
Sea la acción de control:
Figura 1. Referencia de entrada al controlador, variación del nivel de 25 cms a 10 cms. Cada 5000 s.
A. Falla tanque no lineal
La falla en el tanque no lineal se presenta cuando la válvula correspondiente es activada, esta falla es modelada como la variación del valor del área que determina el caudal de salida.
La variación del parámetro se presenta en t=10000 y desaparece en t=20000, donde los resultados de los residuos de presentan en la figura 2.
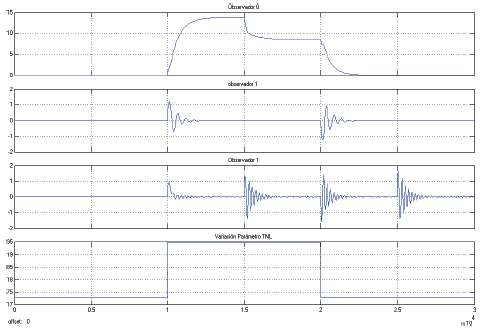
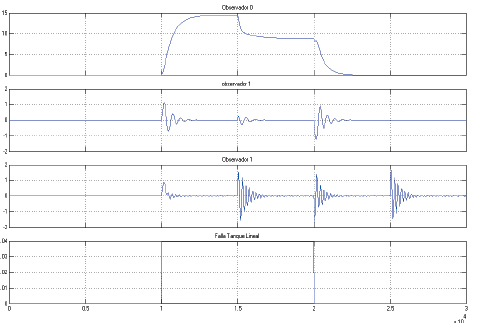
Figura 2. Residuos generados por la variación de Ad
Figura 2: El residuo generado por el observador ordinario (primero desde la parte superior) muestra la presencia de la variación de un parámetro entre t=10000 y 20000. El residuo generado por el observado adaptivo del parámetro Ad (Segundo desde la parte superior) muestra que entre el tiempo 10000 y 11000, el observador detecta la falla y se adapta el parámetro a ésta. El tercer residuo detecta la falla, empieza a realizar la adaptación de la misma, pero en las variaciones del nivel se presentan oscilaciones que muestran que el parámetro Aa no en el que se presentó la falla, en la cuarta parte de la gráfica se presenta la variación del parámetro Ad que corresponde a la falla presentada en el tanque no lineal.
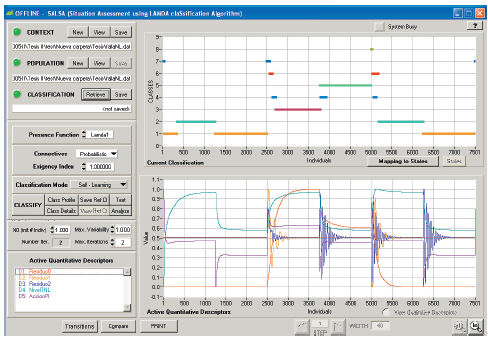
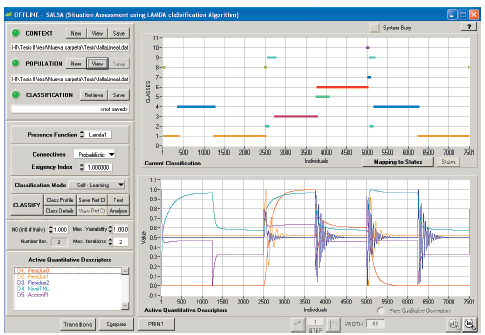
Figura 3. Clases resultantes por los residuos en la variación de Ad. Creación de clases Lamda 1.
Figura 3: En los resultados con clasificación Lamda 1 se pueden determinar con facilidad que las dos clases inferiores son generadas por el sistema libre de fallos y las clases superiores con mayor número de individuos son generadas en los momentos donde se presentan las fallas y las restantes por los transientes presentes en la variación de la referencia.
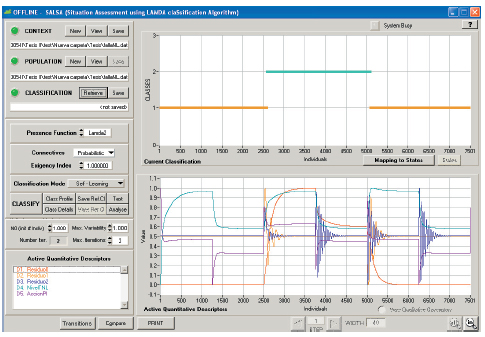
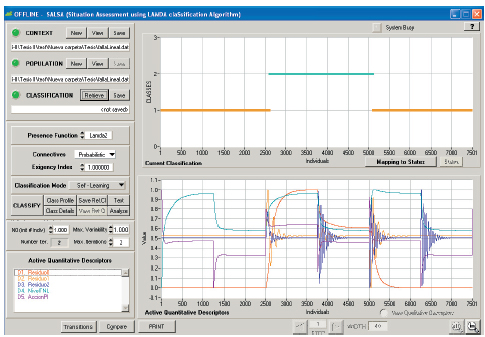
Figura 4. Clases resultantes por los residuos en la variación de Ad. Creación de clases Lamda 2.
Figura 4. Los resultados con clasificación Lamda 2, son más claras las clases, la inferior determina al sistema libre de fallas y la superior en presencia de la falla.
B. Falla tanque lineal
Figura 5. Residuos generados por la fuga en el tanque lineal
Figura 5. Los resultados demuestran que ninguno de los residuos es capaz de adaptarse a la falla presentada, para el residuo 1 en el cambio de nivel (t=15000) se presenta oscilación menor a las generadas en t=10000 y 20000 lo que indica que este parámetro no es en el que se presentó variación al igual que en el residuo 2
Figura 6. Clases resultantes en el sistema en presencia de fuga en el tanque lineal. Creación de clases Lamda 1.
Figura 6. En la presencia de cualquiera de las fallas los resultados en las clases son similares, en la fuga presentada en el tanque lineal hay mayor número de clases, con clasificación Lamda 1, pero igual número en la clasificación Lamda 2 para cualquier falla.
Figura 7. Clases resultantes en el sistema en presencia de fuga en el tanque lineal. Creación de clases Lamda 2.
Figura 7. Al igual que cuando la falla se presenta en el tanque no lineal la clasificación con el cálculo del MAD con Lamda 2, las clases generadas son menores y se puede determinar con mayor facilidad el instante en el que se presentan las fallas.
En el caso que la salida medida del sistema esté en presencia de ruido, la metodología continúa siendo válida si la magnitud del ruido es pequeña comparable con el efecto de la fallas en los residuos generados.
VII. CONCLUSIONES Y PERSPECTIVAS
Los resultados de las simulaciones han mostrado buen desempeño en la detección de las fallas. La generación de los residuos se ha basado en observadores adaptivos diseñados a partir de observadores de alta ganancia, este método es válido tanto para plantas lineales como No lineales.
Para la detección de fallos en varios parámetros al tiempo se requiere de observadores adaptivos con un mayor número de parámetros lo que lo hace más complicado para su diseño, menos realista y más susceptible a fallos en la interpretación de resultados.
Los resultados de la clasificación LAMDA muestran los instantes en los que se presentan las fallas, de así alertar al operador que puede determinar con exactitud la falla observando los resultados generados por los residuos.
El análisis por componentes principales contribuye para minimizar los datos a clasificar sin mayor pérdida de generalidad, para este caso los resultados no difieren mucho al eliminar la variable que por el análisis es la menos representativa.
REFERENCIAS
[1] Q. Zhang Fault detection and Isolation based on adaptive observers for non-linear dynamic systems publication interne no. 1261, IRISA, Rennes, France, 1999. [ Links ]
[2] J. P. Gauthier, H. Hammouri A simple observer for nonlinear systems applications to bioreactors IEEE Trans. On automatic control, 37 (6), 1992: 875- 880. [ Links ]
[3] J. P. Gauthier, A. Kupka, I.A.K. "Observability and observers for nonlinear systems". SIAM Journal Control and Optimization., 32 (4), 1994: 975-994. [ Links ]
[4] C. Isaza, T. Kempowsky, J. Aguilar, A. Gauthier Clasificación Cualitativa con la Metodología LAMDA, Comparación con dos Técnicas de Clasificación Universidad de los Andes. [ Links ]
[5] T. Kempowsky Surveillance de Procédes à base de Méthodes de Classification: Conception d'un Outil d'aide pour la Détection et le Diagnostic des Défaillances. Versión provisional, 2004. [ Links ]
[6] N. Kabbaj, M. Polit. Adaptive Observers based Fault Detection and Isolation for an Alcoholoc Fermentation Process. 8th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA'2001). 2001. [ Links ]
[7] Nakkabi, Youssef., Kabbaj, Nabil "A combined analytical and Knowledge based Method for fault detection and isolation". 2003 IEEE Conference on Emergin Technologies and Factory Automation. [ Links ]