Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista de Ingeniería
versão impressa ISSN 0121-4993
rev.ing. n.24 Bogotá jan./jun. 2006
Determinación de parámetros de fuga para fallas longitudinales, en conexiones domiciliarias y en uniones de tuberías en PVC
Determination of parameters of leaks for longitudinal faults, in connections and PVC pipe joints
Humberto Ávila Rangel
Ingeniero Civil, M.Sc en Ingeniería Civil en el Área de Recursos Hídricos, adelanta estudios de Doctorado en Recursos Hídricos en la Universidad de Alabama. Investigador Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Departamento de Ingeniería Civil, Universidad de los Andes. Bogotá D.C., Colombia.
humbertoavila@gmail.com.
Carolina González Barreto
Ingeniera Civil, M.Sc. en Ingeniería Civil en el Área de Recursos Hídricos (2004). Asesora de la Oficina Técnica en la Comisión de Regulación de Agua Potable y Saneamiento Básico -CRA Investigadora Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Departamento de Ingeniería Civil, Universidad de los Andes. Bogotá D.C., Colombia.
cgonzalez@cra.gov.co
Recibido 6 de febrero de 2006, aprobado 7 de noviembre de 2006.
PALABRAS CLAVE
Fugas, agua no contabilizada, redes de distribución.
RESUMEN
Las fugas en tuberías y accesorios se relacionan con fugas en orificios. Sin embargo, cada tipo de fuga presenta una ecuación potencial en la cual varían los exponentes y los coeficientes de descarga, según el tipo de falla. También se conoce que el caudal de fuga generalmente está relacionado con el área de la falla; pero, muchas veces no es posible determinar este componente geométrico, razón por la cual la ecuación para el cálculo del caudal de fuga debe relacionarse con variables conocidas en la práctica como el diámetro de las tuberías o las longitudes de cada falla, objetivo de esta investigación.
KEYWORDS
Leaks, water distribution network.
ABSTRACT
In general, the pipes and fittings leaks are analyzed like an orifice leak. However, each kind of failure has a particular equation with variable discharge coefficient and exponent. The leak discharge is related with the failure area, but many times it is not possible to calculate this component. Hence, the leak equation must be related with known variables like the pipe diameter or characteristic length of a failure.
INTRODUCCIÓN
En esta investigación se intenta determinar los parámetros y ecuaciones que logren explicar, con una confiabilidad adecuada, el comportamiento hidráulico de fallas longitudinales reales en tuberías de PVC de 2", 2,5", 3" y 4" (50.8, 63.5, 76.2 y 101.6 mm) con una relación diámetro espesor (RDE) equivalente a 21. También se analizan fallas en las uniones de las tuberías y fallas típicas en conexiones domiciliarias, calibrando los parámetros que expliquen el comportamiento hidráulico medido experimentalmente. Todo con el fin de entender las fugas en la redes como una función directa de la presión para poder ser calibradas.
MARCO TEÓRICO
La ecuación general que describe la hidráulica de un orificio en un embalse se deduce a partir de la ecuación de Bernoulli, teniendo en cuenta la diferencias de presiones entre el punto más alto del embalse y la salida en el orificio. La ecuación general de un orificio es de la siguiente forma:
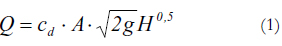
donde, Q es el caudal que sale a través del orificio, (L3T-1); A es el área del orificio, (L2); g es la aceleración de la gravedad (LT-2); H es la altura de agua sobre el orificio (L). El coeficiente de descarga cd, depende de la relación entre la velocidad real Vr y teórica Vt del chorro, así como también de la relación entre el área del orificio Ao y el área del chorro Ach [1], [2].
Para el caso general de fugas en tuberías a presión, tanto el coeficiente de descarga como el exponente, requieren ser calibrados [3], [4]. Por lo tanto la ecuación (1) se simplifica de la siguiente forma:

donde c = coeficiente global de descarga; P = presión en metros de agua. La ecuación (2) es el punto de partida para la calibración de los parámetros c y b, buscando una dependencia con variables conocidas como una longitud característica de la falla y las características de la tubería.
DESCRIPCIÓN DEL MONTAJE
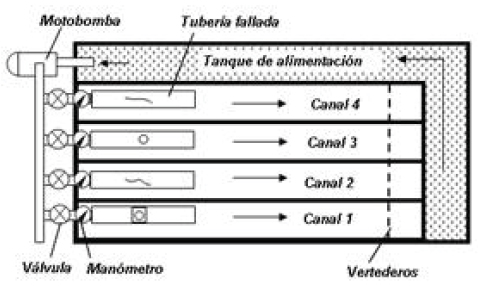
El montaje para la elaboración de las pruebas consistió en un circuito cerrado compuesto por un tanque de almacenamiento de agua, una motobomba, un sistema de alimentación, cuatro canales de prueba y los instrumentos de medición de caudal y presión. En cada una de las entradas a los canales, se instaló una válvula para el control de la presión y un manómetro. Cada canal tenía un vertedero triangular de 60° de cresta delgada para la medición del caudal [5]. Todo el sistema estuvo alimentado por una motobomba con capacidad de 6.0 L/s y 56 m de cabeza dinámica; en la Figura 1 se ilustra un esquema del montaje para las pruebas.
Figura 1. Esquema del montaje: Se describe el sentido del flujo del agua por medio de flechas. Los vertederos se esquematizan con una línea punteada para describir su ubicación.
El procedimiento experimental consistió en la generación de la falla en una tubería de diámetro específico. Luego la tubería se adapta a una de las alimentaciones de agua en cada canal. Posteriormente, se somete a presión mediante la motobomba y se mide la presión del agua con un manómetro, localizado inmediatamente aguas arriba de la falla y el caudal con el vertedero triangular. La válvula localizada aguas arriba del manómetro permite variar y controlar la presión. Cada par de medidas presión - caudal en una falla específica constituye un punto de la curva de presión- caudal con la cual se calibraron los parámetros para lograr el mejor ajuste en la ecuación (2).
PROCEDIMIENTO DE CALIBRACIÓN
El procedimiento de calibración consistió en la determinación de los parámetros c y b de la ecuación (2) para cada una de las pruebas realizadas, mediante simulaciones de Monte-Carlo [6]. Esta calibración inicial se realizó para las fallas longitudinales, fallas en conexiones domiciliarias y fallas en uniones de tuberías, y se denomina Calibración tipo I. Posteriormente, para las fallas longitudinales, se realizó una calibración para relacionar los parámetros c y b con variables conocidas (diámetro y longitud de falla). Se empleó la siguiente secuencia de calibración:
Calibración tipo II: Determinación de un coeficiente global de descarga c, en función de la longitud de la falla L. También se realizó la calibración del exponente b, en función de la longitud y del diámetro, utilizando dos criterios. La ecuación a calibrar es la siguiente:

donde, m y n = parámetros a calibrar. Para el exponente b, se utilizaron dos criterios de calibración, que son:
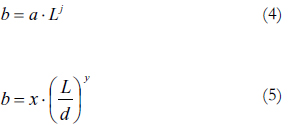
Posteriormente, después de la calibración de la ecuación (5) (Criterio 2), se determinó que el valor de b puede ser 1.70; siendo éste el tercer criterio.
Calibración tipo III: Determinación de los coeficientes globales de descarga, manteniendo los exponentes con los criterios 2 y 3.
Calibración tipo IV: Determinación de la dependencia de los coeficientes de descarga en función de la longitud para cada diámetro analizado.
Calibración tipo V: Determinación de la dependencia del coeficiente global de descarga con el diámetro de la tubería.
PRUEBAS REALIZADAS
En la investigación se realizaron pruebas para fallas longitudinales, conexiones domiciliarias y las uniones de las tuberías (unión Z), las cuales se especifican en las Tabla 1 y 2:
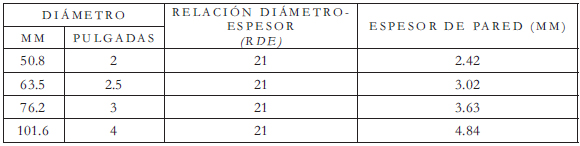
Tabla 1. Características de las tuberías de PVC ensayadas con fallas longitudinales reales
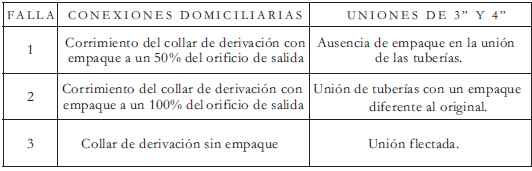
Tabla 2. Características de las fallas en las tuberías de PVC ensayadas
CALIBRACIÓN TIPO I
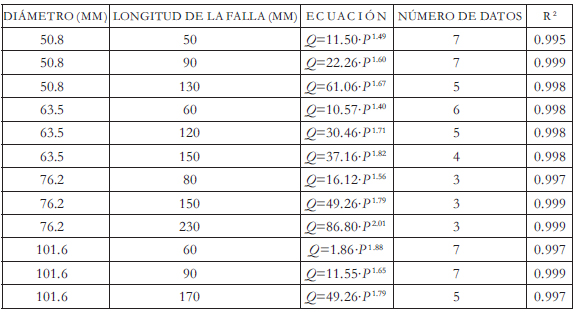
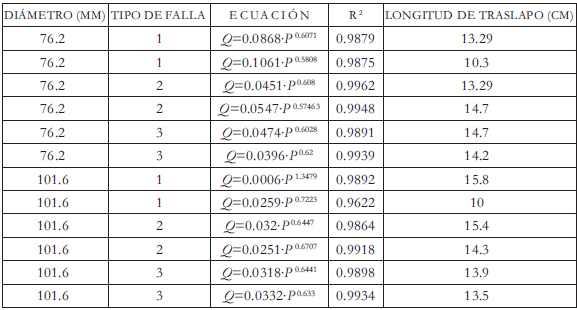
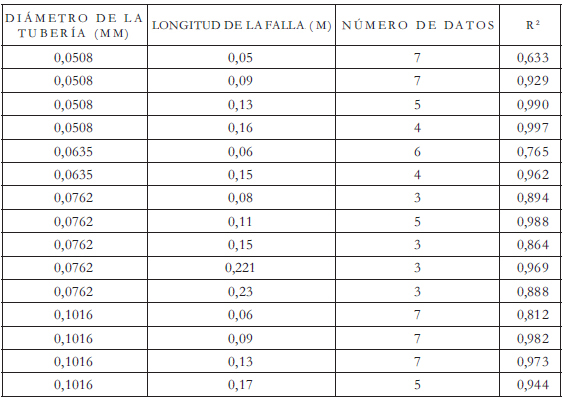
Los parámetros de fuga c y b de la ecuación (2) son el punto de partida para la determinación de la dependencia del caudal de fuga con respecto a variables conocidas (diámetro de tubería, longitud de la falla evaluada). Para las fallas en conexiones domiciliarias y en uniones, el proceso de calibración sólo llega hasta este punto. Sin embargo, se analizaron los resultados obtenidos para cada caso. Algunos de los resultados de las pruebas en fallas longitudinales y en conexiones domiciliarias se presentan en la Tabla 3 y 4, respectivamente. La Tabla 5 presenta los resultados de la calibración para las pruebas de fallas en uniones de tuberías las cuales fueron evaluadas con 5 datos por experimento; en la columna 5 se establece la longitud de traslapo, la cual se refiere a la longitud de la zona de sobreposición de las dos tuberías en la unión específicamente.
Tabla 3: Resultados de la calibración en pruebas de fallas longitudinales reales
Tabla 4: Resultados de la calibración en pruebas de fallas en conexiones domiciliarias
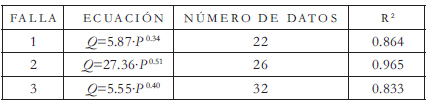
Tabla 5: Resultados de la calibración en pruebas de fallas en las uniones de las tuberías
Para las fallas longitudinales, se realizó una deducción del exponente y el coeficiente global de descarga en función del diámetro y la longitud de la falla. Esta deducción se muestra en las siguientes calibraciones. Para el caso de las fugas en conexiones domiciliarias, se observa que los exponentes tienden a comportarse como un orificio, pero en algunos casos el exponente es menor a 0.5. Este hecho se debe a que se genera un estrangulamiento del orificio de salida por el collar de derivación.
En las fallas producidas en las uniones, los exponentes presentan una pequeña variación con el diámetro de la tubería; es decir, para los mismos ensayos, los exponentes son menores en las ecuaciones obtenidas para las tuberías de 3" que los exponentes de las ecuaciones de las tuberías de 4". Para los ensayos sobre la tubería de 3", se obtuvo exponentes alrededor de 0.5 y 0.6, es decir, las fugas tienden a comportarse como un orificio; sin embargo, el caudal de fuga es mayor que si la falla ocurriera sobre un área circular. Por otro lado, los coeficientes de descarga giran en torno al valor 0.05, disminuyendo de acuerdo con la longitud de traslapo entre las dos tuberías ensayadas. En el caso de las tuberías de 4", los exponentes fueron mayores que 1 para los ensayos de tuberías sin empaque, en donde el caudal de fuga fue bastante alto. Para los demás ensayos, los exponentes variaron alrededor de 0.6, independiente del tipo de falla probado. Esto último indica que las fugas producidas en las uniones de las tuberías tienden a comportarse como un orificio, con un caudal de salida mayor que si el área de falla se presentara circular. Los coeficientes de descarga obtenidos para 4" son mucho más bajos que para los ensayos en 3". Para el tipo de falla 1 los valores de los coeficientes son bastante pequeños; para las fallas 2 y 3 los coeficientes oscilan entre 0.02 y 0.05. También se determinó que el caudal de fuga es inversamente proporcional a la longitud de traslapo en la unión; es decir, cuando esta longitud disminuye el caudal de salida aumenta.
CALIBRACIÓN TIPO II
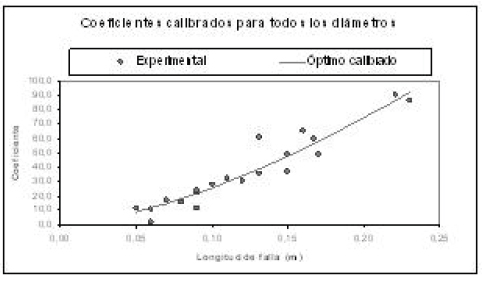
En esta calibración se agruparon todos los coeficientes de la Tabla 3, sin discriminar los diámetros. En la Figura 2, se muestra la curva calibrada para el coeficiente global de descarga.
Figura 2. Calibración de los coeficientes de descarga en función de la longitud de la falla L sin discriminar diámetros
La ecuación obtenida para la curva calibrada (R2 = 0.905) es:

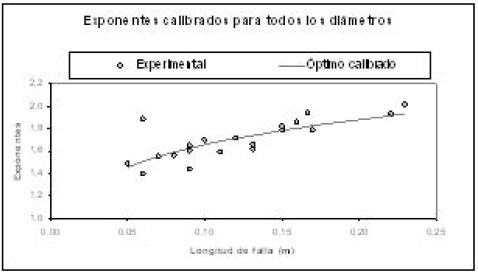
De igual manera, se agruparon los exponentes y se calibraron los dos primeros criterios. Para el criterio 1, mostrado en la Figura 3, se obtuvo la siguiente ecuación (R2 = 0.816):

Figura 3. Calibración de los exponentes mediante el criterio 1
Para la calibración del exponente con el criterio 2, se obtuvo la siguiente ecuación:
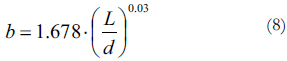
El coeficiente de correlación (R2) de la ecuación (8) es bajo en términos de ajuste, teniendo en cuenta que la longitud de la falla (L) es una variable aleatoria. Sin embargo, la importancia de la ecuación radica en que los valores de L/d están dispersos en un rango entre 1.4 y 2.0, el cual es relativamente pequeño. Luego, a partir de la calibración del exponente b con el criterio 2, se determinó un tercer criterio donde

Entonces, la primera aproximación a una ecuación general para las fugas en fallas longitudinales está expresada como:

donde b depende de cualquiera de los tres criterios calibrados de las ecuaciones (7), (8) o (9).
Ésta es la primera aproximación a la ecuación general para fugas en fallas longitudinales, pero no logra explicar bien el comportamiento de éstas al ser relacionada con los datos experimentales. Esto se debe a que no se tuvo en cuenta el efecto que tiene el espesor de la tubería, el cual al incrementarse dificulta el aumento del área de la falla en función de la presión. Enton- ces, se relacionará el coeficiente con los diámetros de cada tubería, pues se está manteniendo constante el RDE para todas las tuberías ensayadas.
CALIBRACIÓN TIPO III
En esta calibración, se determinaron nuevamente los valores de los coeficientes de descarga para cada uno de los diámetros, como se realizó en la calibración tipo I, pero utilizando los criterios 2 y 3 de los exponentes b. Estos resultados serán los datos de entrada para la calibración de un parámetro m (ecuación 11) que permita visualizar el efecto que tiene el diámetro sobre el coeficiente de descarga.
CALIBRACIÓN TIPO IV
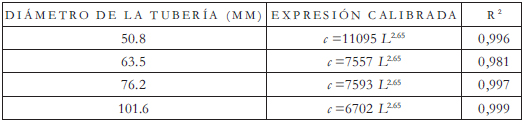
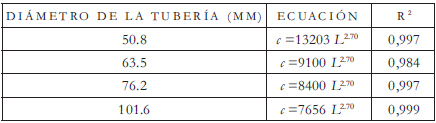
En la calibración tipo IV, se determinó el parámetro m de la ecuación (3), manteniendo el parámetro n = 2.65 para el criterio 2 y n = 2.70 para el criterio 3 del exponente. La selección de los valores de n para cada criterio presentado se realizó con base en el análisis de todos los valores de n durante la parte inicial de la calibración IV. A partir de las calibraciones realizadas para cada diámetro, se obtuvieron las ecuaciones presentadas en las Tabla 6 y 7.
Tabla 6. Expresión para el coeficiente global de descarga en función de la longitud de la falla con el criterio 2 para el exponente b, manteniendo constante el exponente n = 2.65
Tabla 7. Expresión para el coeficiente global de descarga en función de la longitud de la falla con criterio 3 para el exponente b, manteniendo constante el exponente n = 2.70
De las tablas anteriores se pudo observar la tendencia decreciente del coeficiente m, en función del diámetro. Esto permitió concluir que el espesor de la tubería tiene un efecto importante en cuanto a la dificultad de incrementar el ancho de la falla, al aumentar la presión para tuberías de diámetros mayores manteniendo un RDE constante.
CALIBRACIÓN TIPO V
La calibración tipo V determina la dependencia del parámetro m en función del diámetro. Esta calibración se realizó mediante la siguiente expresión:

donde p y q son los parámetros a calibrar.
Para los criterios 2 y 3, se obtuvieron las siguientes expresiones:
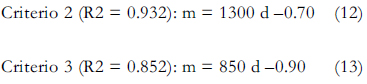
Finalmente, teniendo todos los parámetros calibrados, se obtuvo dos ecuaciones para describir el com-portamiento hidráulico de las fallas longitudinales.
Estas ecuaciones son:
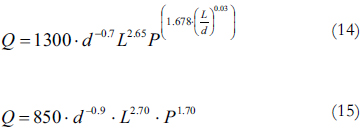
Se puede utilizar cualquiera de las dos ecuaciones anteriores para calcular el caudal de fuga a través de una falla longitudinal. Sin embargo, la ecuación (14) tiene un mejor ajuste global con los datos experimentales medidos, con un valor de R2 igual a 0.91. La ecuación (15) por su parte tiene un grado de ajuste menor de R2 = 0.88, pero tiene la ventaja de ser una ecuación más sencilla; los ajustes entre la ecuación (14) y los datos experimentales se muestran en la Tabla 8.
Tabla 8: Resultados del análisis de la ecuación general calibrada (14) con respecto a los datos experimentales medidos
CONCLUSIONES
Las fallas reales en las redes de distribución tienen un comportamiento diferente a la hidráulica de un orificio en un embalse. Los exponentes obtenidos para las fallas longitudinales varían entre 1.5 y 1.8, mientras que en las conexiones domiciliarias y las fallas en uniones de tuberías de 3" y 4" varían entre 0.3 y 0.6.
Las características plásticas de las tuberías de PVC inducen a una dependencia entre el área de una falla longitudinal, el diámetro o el espesor de la tubería, y la presión. Al incrementar el diámetro de la tubería, con un RDE constante, el caudal de fuga disminuye debido a que el espesor de la pared de la tubería es mayor, dificultando el aumento del ancho de la falla en función de la presión.
Las fallas en conexiones domiciliarias tienden a comportarse como un orificio estrangulado por el collar de derivación. Sin embargo, aunque esto implique un menor caudal de fuga en comparación a un orificio, la presencia de muchas de estas fallas en una red de distribución de agua potable significa una pérdida considerable de agua y de dinero.
Las fugas en uniones de tuberías presentan una tendencia a comportarse como un orificio en un embalse; sin embargo, la relación entre la presión y el caudal de fuga presenta un exponente superior a 0.5 en la mayoría de los casos. Las ecuaciones de fugas presentadas por la ausencia de empaque tienen un exponente mayor que uno, debido al gran caudal que puede salir por esta falla.
Los demás tipos de fallas que han sido probados tienen exponentes alrededor de 0.6, lo que significa que el caudal es mayor a lo esperado en un orificio de un tanque o embalse con las mismas características.
El comportamiento hidráulico de las fallas en tuberías de agua potable es un horizonte que debe ser explorado para tener un conocimiento más claro de la hidráulica de las redes bajo ambiente de fugas.
REFERENCIAS
[1] R. Street, G. Watters, J. Vennard. Elementary fluid Mechanics. Séptima edición. Editorial Hohn Wiley and Sons. Inc., 2000. [ Links ]
[2] V. Streeter, E. Benjamín Wylie, K. Bedford. Fluid Mechanics. Novena Edición. Editorial Mc Graw Hill. 1984. [ Links ]
[3] R. Pudar y J. Ligget. "Leaks in pipe networks". Journal of hydraulic engineering. ASCE. Vol 118 N° 7. Julio 1992. [ Links ]
[4] T. Tuccarelli, A. Criminisi y D. Termini. "Leak Analysis in pipeline systems by means of optimal valve regulation". Journal of hydraulic engineering. ASCE. Vol 125 N° 3. Marzo 1999. [ Links ]
[5] S. Trueba. Hidráulica. Editorial Compañía editorial continental S.A., 1979. [ Links ]
[6] M. Lees, W. Thorsten. Monte-Carlo Análisis (MCAT) v.2. Department of Civil Engineering - Imperial Collage. 2000. [ Links ]