Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista de Ingeniería
versão impressa ISSN 0121-4993
rev.ing. n.24 Bogotá jan./jun. 2006
Aerodynamic Characteristics of Airfoils with Blunt Trailing Edge
A. Gómez
M.Sc. Dept. of Mechanical Eng. Universidad de los Andes. Now Ph.D. student at the University of Hannover, Germany.
gomez@tfd.uni-hannover.de
Álvaro Pinilla
Ph.D, M.Sc. Professor of the Mechanical Engineering Dept. Universidad de los Andes. Bogotá D.C., Colombia.
apinilla@uniandes.edu.co
Recibido 13 de marzo de 2006, aprobado 1 de junio de 2006.
PALABRAS CLAVE
Aerodinámica, Perfiles Aerodinámicos, CFD, Energía Eólica, Aerogeneradores.
RESUMEN
El siguiente trabajo estudia de manera computacional el comportamiento de las características aerodinámicas de perfiles NACA (National Advisory Committee for Aeronautics, hoy conocido como NASA), con modificaciones en el borde de salida. Las modificaciones consisten en remover secciones del borde de fuga del perfil. La investigación realizada estudia 39 perfiles diferentes de la familia NACA de 4 dígitos, con modelos teóricos sencillos para explicar los fenómenos. Los resultados muestran los cambios en las características de sustentación y arrastre del perfil, y cambios en cuanto a la entrada en pérdida del mismo.
KEYWORDS
Aerodynamics, Blunt Trailing Edge, Aerodynamic Profiles.
ABSTRACT
This paper is a computational study of the behaviour of aerodynamic characteristics of NACA (National Advisory Committee for Aeronautics, today known as NASA) profiles with tailored trailing edges. 39 different profiles 4-digit NACA family were studied during the research. A computational research was made, using simple theoretical models to explain and to understand the results. The results describe the changes in lift and drag characteristics and changes in stall angle of attack.
SYMBOLS
a Radius of circle for conformal mapping
a1 Parameter of Gaussian parameterization
b1 Parameter of Gaussian parameterization
c1 Parameter of Gaussian parameterization
c Chord
Cd 2- D Drag coefficient
Cd0 Minimum value of Cd
Cl 2-D Lift coefficient
D Drag force
F Force
i Imaginary unit
l Variable for the Joukowski transformation
L Lift force
m Slope of the lift curve
p Pressure
s Complex variable for circle displacement in conformal mapping
u x-component of velocity
v y-component of velocity
w Complex potential
z Complex variable for conformal transformation
α Angle of attack of the profile
α0d Angle for minimum Cd
α0l Angle for which Cl = 0
αl/d max Angular position for the maximum Cl/Cd ratio
β Absolute incidence angle
δ Boundary layer thickness
ζ Complex variable for conformal transformation
η Slope of b1 vs. Λ
ξ Slope of a1 vs. Λ
θ Angle for conformal mapping
Λ Percentage of the chord cut-off at the trailing edge
μ Parameter to describe drag
INTRODUCTION
Traditionally, airfoil geometries are such that they have a rounded leading edge and a sharp trailing edge. It would be useful in some cases, to use airfoil geometries which are thicker, in order to attain better structural performance. The following paper studies the effects on the aerodynamic performance caused by modifications made to the trailing edge of subsonic profiles, intended for use in wind turbines. The type of modifications proposed can be summarized as cutting off the trailing edge perpendicular to the chord line of the profile at different positions along the chord. In the early 1950's, NACA (National Advisory Committee for Aeronautics) undertook a series of investigations to conclude about the benefits of tailoring the trailing edge of supersonic and transonic profiles [1-4]. The conclusions of these studies can be summarized as an increase in the maximum lift coefficient, and increase in profile drag, and an increase in the lift coefficient slope. The following paper studies similar results for subsonic profiles. The results found include an increase of maximum lift coefficient, a delay in stall and an increase in profile drag. This paper describes how the Cl, Cd, and Cl /Cd curves change as modifications to the trailing edge are made.
Delay in stall of the airfoil could be advantageous for applications such as acrobatic flight, where high angles of attack are needed before the profile stalls. For wind turbines, the fact that higher angles of attack can be reached before entering stalled conditions means that some unsteady effects can be avoided. Namely, when wind gusts or sudden change of wind direction occur, some sections of the wind turbine can stall. This happens mainly in the inboard region of the blade, where the relative wind speed is lower (and thus more sensitive to variations in angle of attack). These effects can last some time before the boundary layer reattaches (leading edge reattachment) and induce unsteady loads on the rotor blades, which in turn reduce the blades life.
The use of blunt trailing edge profiles for wind turbines at the root of the blades would increase the blade's structural strength. Although the increase of profile drag is responsible for a reduced overall efficiency of the rotor, the disadvantages of a decreased efficiency are overcame, due to the fact that the inboard section of the blades do not account for the mayor part of the power generated. The mayor part of the power generated comes from the blade sections at radial stations between 60-90% of the blade's radius.
In order to understand the aerodynamic characteristics of profiles, a thorough knowledge of the effects that the geometry has on the overall aerodynamic performance is required. It is useful to study theoretically the lift and drag characteristics. For this purpose, Joukowski profiles are studied, along with the theoretical solution of inviscid potential flow around them. Additionally, simple mathematical models are proposed in order to understand, at least in a qualitative manner, the general aspects of the profile's drag and lift after modifications have been made to the trailing edge.
For the purpose of understanding the effects of tailoring the trailing edge, 3549 computer simulations were undertaken for 39 different profiles, cutting off the trailing edge at 7 different chord positions, varying the angle of attack between 0° and 14.6°.
AIRFOIL GEOMETRY
In order to make a computational equivalent of the geometry of the profiles, the original paper presented by NACA in 1932 was used [5]. This paper describes the method used to approximate the profile curves using polynomials.
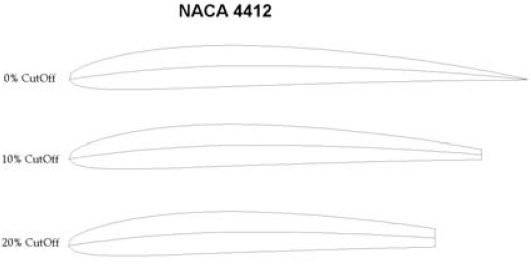
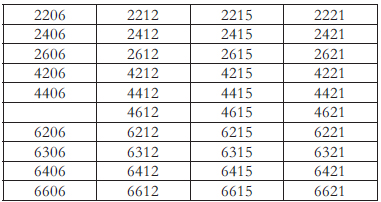
The studied profiles are as those shown in Fig. 1, which illustrate the type of modifications proposed. The different families of airfoils that were studied correspond to the NACA profiles listed in Table 1. Each of these is composed of different modified airfoils with cut-offs at the trailing edge, ranging from 0% to 30% of the chord, in increments of 5%.
Figure 1. Modified airfoils at Λ = 0,0.1 and 0.2
Table 1. NACA 4-digit series profi les studied
The profiles were chosen such that a wide range of relative profile thicknesses could be studied, along with different camber geometries.
COMPUTATIONAL SIMULATION
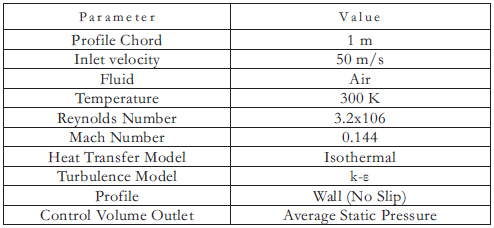
For the CFD simulation, ANSYS CFX was used along with ANSYS CFX-Mesh. A computational control volume around the airfoil is constructed with dimensions 15m × 7m. The grid was constructed using an unstructured mesh and the profile's surface was made up of 2-D extruded elements of 0.01m in length. Additionally, 14 elements within a 5mm region perpendicular to the profile's surface were used to account for boundary layer effects. The inlet and outlet conditions of the control volume consisted respectively of a constant velocity field and an averaged pressure output of 0 Pa (relative to atmospheric pressure). The simulation accounts only for 2-D incompressible flow effects. Table 2 summarizes the parameters used in the simulations.
Table 2. Simulation parameters
For each of the simulations that were run, an independent geometry file, mesh, and boundary conditions definition file were needed. The complete study of one family of airfoils requires 91 different simulations. Drag forces are caused mainly by two factors. The first one is pressure induced drag, and the second one is viscosity induced drag [6]. Pressure induced drag deals with pressure differences throughout the profile's length, with the pressure at the leading edge being greater than at the trailing edge. Viscosity induced drag deals with boundary layer effects due to the shear forces acting on the fluid. Boundary layer thickness is assumed to be:
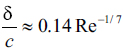
COMPUTATIONAL RESULTS
The CFD simulations are used to produce curves of lift and drag coefficients versus angle of attack of the airfoil. Additionally, the curves of Cl/Cd are also plotted.
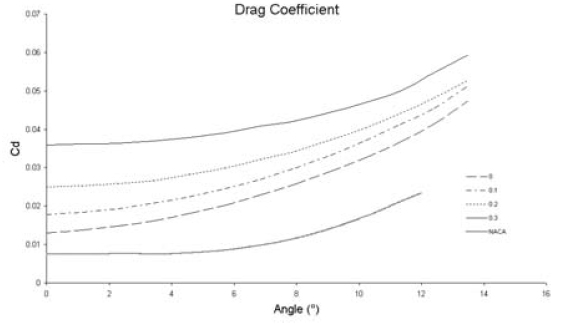
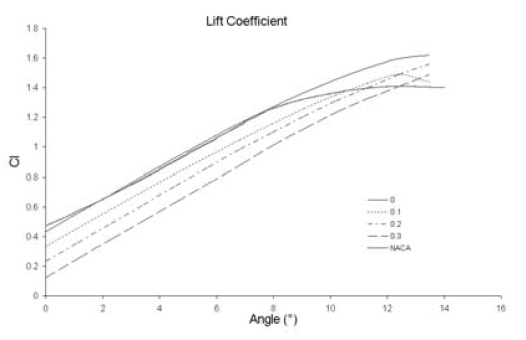
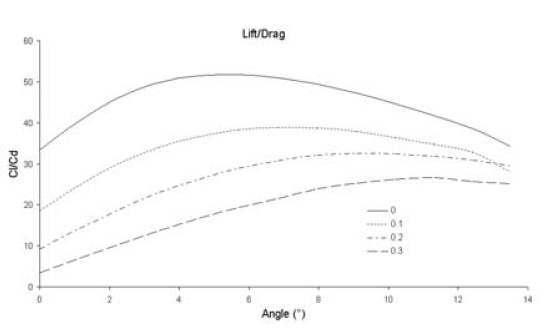
Figures 2 to 4 depict an example of the data obtained with the CFD analysis for the NACA 4415 profile, with modifications ranging from 0% cut-off (original airfoil) to 30% cut-off.
Figure 2. 2-D Drag Coefficient for NACA 4415 [7] for Λ = 0, 0.1, 0.2 and 0.3
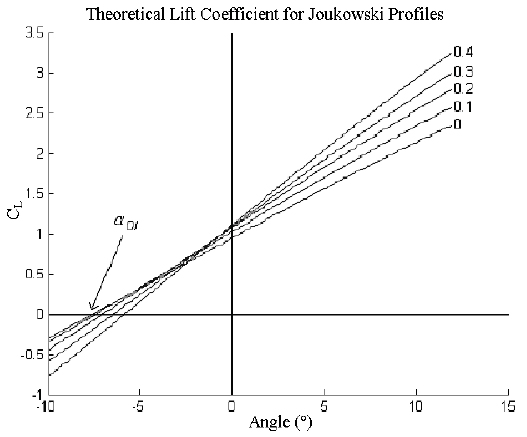
Figure 3. 2-D Lift Coeffi cient for NACA 4415 [7] for Λ = 0, 0.1, 0.2 and 0.3
Figure 4. 2-D Lift/Drag ratio for NACA 4415 [7] for Λ = 0, 0.1, 0.2 and 0.3
The most important characteristics of this family of curves may be summarized as follows:
This last characteristic is presumably a consequence that a blunt trailing edge poses a slightly greater resistance to trailing edge separation, due to vortex convection in the stagnation region. This leads to a delay in vortex formation at the trailing edge. There is no computational evidence of the presumption.
In wind turbine applications, the blade's geometry is such that angle of attack of the profile coincides with αCl/Cdmax for nominal power generation. For this reason, the characterization of this curve is very relevant.
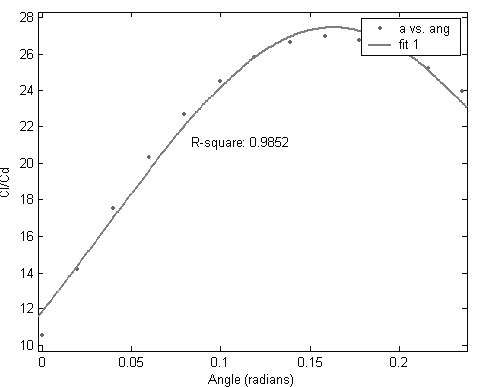
For each of the profiles, a Gaussian curve of the form
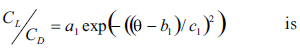
fitted to each of the Cl/Cd graphs (see Fig. 5). The parameters a1, b1 and c1 are to be determined by means of minimum squares methods. For each of the different cut off lengths these parameters are found to be different. A relationship between these parameters and the percentage of cut off at the trailing edge is also found.
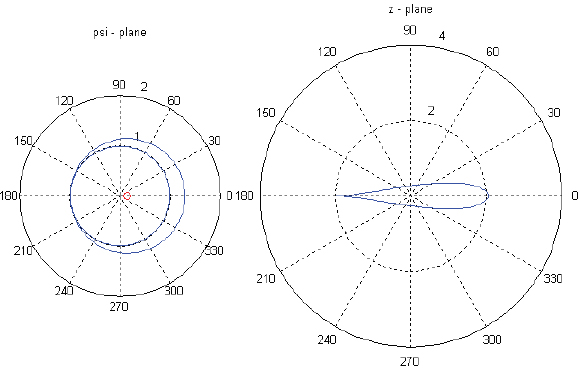
Figure 5. Gaussian fit for Cl/Cd for the NACA 6421 with a 20% cut-off. (Drawn with MatLab ©)
A Gaussian fit of this type is useful, because parameters a1 and b1 explicitly represent two very important aerodynamic characteristics, namely the 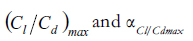 respectively. This parameterization allows a1 and b1 to be studied as functions of Λ (cut-off length), thus giving a description of the profile's response to trailing edge modifications. Using this parameterization, a correlation between the profile's response to these modifications and its geometrical parameters can be established.
respectively. This parameterization allows a1 and b1 to be studied as functions of Λ (cut-off length), thus giving a description of the profile's response to trailing edge modifications. Using this parameterization, a correlation between the profile's response to these modifications and its geometrical parameters can be established.
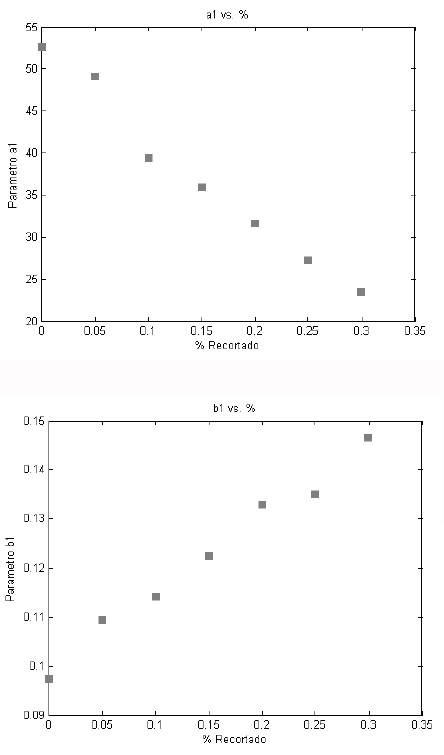
If Λ denotes the cut-off length as a number between 0 and 0.3, then the different parameters can be expressed as a function of Λ for each of the families of airfoils. An example of such parameterizations is shown in Figures 6 and 7. It is interesting to note that the behaviour of parameters a1, b1 and c1 is linear with Λ. These figures depict an example for the profile NACA4415. It is clear from Fig. 6, that when Λ increases, parameter a1 decreases linearly, that is,
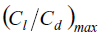
decreases in proportion to the amount of trailing edge removed. The slope of this line represents a response variable, which is unique to the profile, and describes the sensibility of the profile to the modifications. Steeper slopes (more negative) are a sign of rapid degradation of aerodynamic characteristics as a consequence of trailing edge modifications. In regard to parameter b1, it can be seen that it increases linearly as Λ increases. The slope of this curve is again a response variable, indicating the degree of sensibility of the profile to the modifications. Larger slopes indicate a more rapid displacement of the
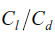
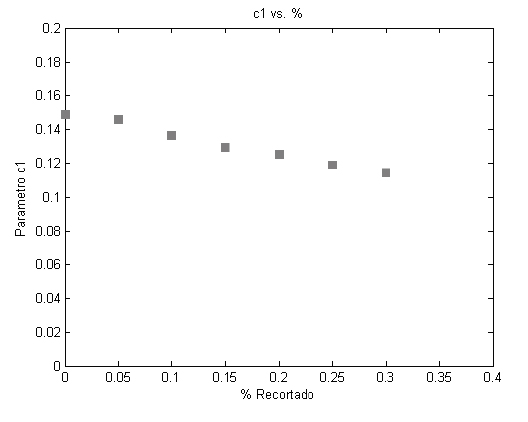
curves to the right (that is a more rapid increase in αCl/Cdmax). Figure 7 shows the variation of parameter c1, which is in direct relation with the drag coefficient of the profile. From the Gaussian fit it is clear that smaller values of c1 represent a narrower curve. This is a consequence of a rapid increase in drag coefficient at high angles of attack (thus reducing the Cl/Cd ratio). Following this parameterization, the 39 studied profiles can be grouped according to a1, b1 and c1 as functions of Λ. For each of the parameters a1 and b1 there are two governing variables, namely y-intercept (value of a1 or b1 for Λ = 0) and slope
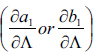
Figure 6. Parameters a1 and b1 for different Λ's - Airfoil NACA 4415. (Drawn with MatLab ©)
Figure 7. Parameter c1 for different Λ's for airfoil NACA 4415. (Drawn with MatLab ©)
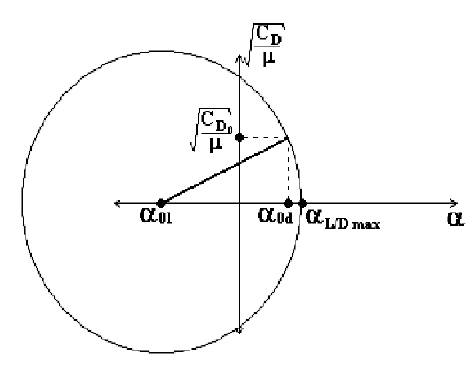
Figure 8. Geometrical representation of αl/dmax
The y-intercept represents a parameter of the profile itself (Λ = 0 means no modification to the trailing edge), while the slope represents a parameter of the response to tailoring the trailing edge. The y-intercept of parameter a1 represents the maximum Cl/Cd relationship for untailored profiles, and the y-intercept of b1 represents the angle at which it occurs.
The results of these parameterizations can be seen in Appendix A and B. The graphs on the appendices A and B collect the studied profiles according to their relative thickness and camber. These figures show how depending on these two geometrical features (thickness and camber) the profile's aerodynamic characteristics vary more or less when modifications are made at the trailing edge.
The plots presented in the appendices are guidelines to predict a profile response to trailing edge modifications, correlated with geometrical parameters as thickness and camber. It is seen in Appendix A that thicker profiles are more sensitive to alterations at the trailing edge. This is can be read from the plot as a lower value of ξ (slope of a1). For applications in which high Cl/Cd are desired, relatively thin profiles should be used. Larger camber also has as consequence lower values of ξ (steeper -more negative- slopes). Appendix B shows the correlation between parameter b1 and the profile's thickness and camber. It can be seen that profiles with greater thickness and camber achieve greater displacements of αCl/Cdmax. This can be read as greater values of η, which is the slope of the curve b1 vs. Λ.
Thus, a compromise must be made between loss in aerodynamic performance and an increase in αCl/Cdmax. For wind turbines at the inboard section, an increase of aCl/Cdmax is readily translated into lower pitch angles, which in turn results in a more linear distribution of the blade's pitch positioning, and thus a cheaper manufacture. Having these profiles in the inboard region increases the structural stability of the blade because of higher area moments of inertia, and also reduced stress at the root of the blade. The penalty is a lower aerodynamic performance, but as said in the introduction, the inboard section of the blade is not responsible for the mayor percentage of power generation.
EFFECTS OF LIFT AND DRAG OVER CL/CD
In the process of designing rotor blades for applications such as wind turbines, compressors, fans, etc., having a good understanding of the Cl/Cd curves can prove more useful than the Cl and Cd curves alone [8,9]. This is due to the fact that the rotor blades are designed such that at every radial position the profile makes an angle αCl/Cdmax with respect to the relative wind speed (assuming nominal power extraction and a constant wind field). For this reason, it is important to understand, which factors determine the position of this maximum, and what influence Cl and Cd have over it. For the following analysis only the linear region of the Cl curve is considered. For small incidence angles, the lift curve can be approximated to a first order polynomial, and the drag curve can be approximated to a second order polynomial. Such parameterizations are as stated in Eq. (1).
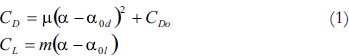
The lift/drag curve can be expressed as
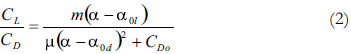
Finding the maximum for Eq. (2) the result is:
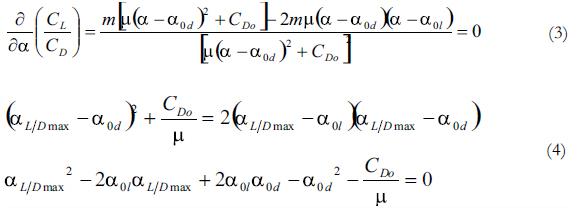
Equation (4) can be solved to obtain the angle at which the curve of Cl/Cd is at its maximum.
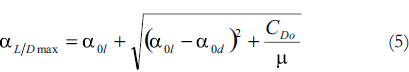
A quick inspection of Eq. (5) allows it to be represented geometrically, as shown in Fig. 8. The angles α0l and α0d represent the angle at which the value of the lift coefficient equals 0, and the angle at which the drag coefficient is a minimum respectively. Cd0 is the value of the drag coefficient corresponding to α0d.
Analyzing Fig. 8, it is seen, that probably the most significant variations on αl/dmax can be obtained by displacing the angle α0l to the right or increasing Cd0, which is precisely what happens as the cut-off length increases. Making this angle larger also reduces the value of the maximum Cl/Cd relation, which is also reduced by the fact that Cd0 becomes bigger as the cut-off length increases. The latter analysis is developed for the sake of understanding the individual effects of Cl and Cd on αl/dmax.
SOLUTION OF JOUKOWSKI PROFILES
Making use of a conformal transformation of the form 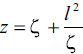 , being z and ζ complex variables, a circle in the ζ space, as represented by
, being z and ζ complex variables, a circle in the ζ space, as represented by 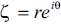 can be transformed into profiles with different characteristics as it is shown ahead [6]. This transformation has the characteristic of mapping a circle or radius l in the ζ- plane into a straight horizontal line in the z plane. Circles in the ζ plane with radius greater than l will be mapped into ellipses. Thus, applying this transformation to circles whose centres lie on the real axis of the complex plane, these can be mapped into profiles which have an elliptic leading edge and sharp trailing edge. Circles whose centres lie on the imaginary axis of the complex plane ζ will be mapped into cambered lines. Thus combining both transformations, a circle on the ζ- plane given by
can be transformed into profiles with different characteristics as it is shown ahead [6]. This transformation has the characteristic of mapping a circle or radius l in the ζ- plane into a straight horizontal line in the z plane. Circles in the ζ plane with radius greater than l will be mapped into ellipses. Thus, applying this transformation to circles whose centres lie on the real axis of the complex plane, these can be mapped into profiles which have an elliptic leading edge and sharp trailing edge. Circles whose centres lie on the imaginary axis of the complex plane ζ will be mapped into cambered lines. Thus combining both transformations, a circle on the ζ- plane given by 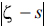 can be transformed into an aerodynamic profile with a cambered chord line with an elliptic leading edge, and a sharp trailing edge. The family of profiles obtained is called the Joukowski profiles (see Fig. 9) [6]. Writing the complex potential w for the flow around a circle of a uniform wind of speed V and incidence angle α, the velocity can be found in the ζ-plane.
can be transformed into an aerodynamic profile with a cambered chord line with an elliptic leading edge, and a sharp trailing edge. The family of profiles obtained is called the Joukowski profiles (see Fig. 9) [6]. Writing the complex potential w for the flow around a circle of a uniform wind of speed V and incidence angle α, the velocity can be found in the ζ-plane.
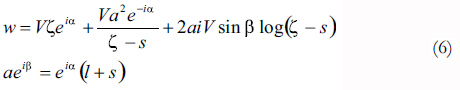
Figure 9. General Joukowski profile. (Drawn with MatLab ©)
Then, the velocity in the z-plane can be found as
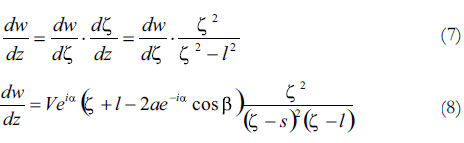
The velocity is then 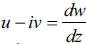 . With the velocity field and knowing the pressure far away from the profile, Bernoulli's equation can be used to find the pressure distribution throughout the profile and in this manner compute the total force acting on the profile due to pressure alone.
. With the velocity field and knowing the pressure far away from the profile, Bernoulli's equation can be used to find the pressure distribution throughout the profile and in this manner compute the total force acting on the profile due to pressure alone.
The theoretical lift curve is computed after finding the total force per unit length on the profile which is of the form 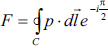 . The term
. The term 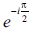 indicates a rotation of 90° in the clockwise direction, so that the pressure acts perpendicular to the surface of the profile.
indicates a rotation of 90° in the clockwise direction, so that the pressure acts perpendicular to the surface of the profile.
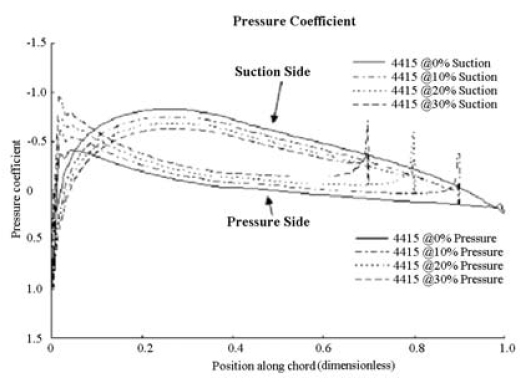
To simulate the effect of tailoring the trailing edge, the same integral may be computed, but omitting the forces on the percent of the chord to be cut off. These results can be seen in Fig. 11. The fact that this computation may indeed be done as a first approximation to the theoretical solution of the problem, lies in the fact that the pressure distributions vary little when the trailing edge is tailored (see Fig. 10). The flow doesn't "know" about the tailored trailing edge ahead. The only difference in the pressure distributions will be a greater pressure (less suction) on the suction side of the profile due to increased trailing edge dead fluid pressure.
Figure 10. Pressure coefficient for modified profiles
It can be seen from the results how a0l displaces itself to the right as the cut-off length increases. These results are computed considering a potential flow around the airfoil, which is clearly not the case due to the separation that occurs at the trailing edge. The latter analysis does not take into account the fact that the stagnation region behind the profile increases the trailing edge pressure. This has as a consequence a reduction of fluid speed on the suction side of the profile, and thus greater static pressure (Bernoulli's equation). Having greater static pressure on the suction side of the profile causes a decrease in the lifting force, and thus lower values of Cl as seen in Fig. 11.
Figure 11. Effects on Cl due to tailoring the trailing edge. (Drawn with MatLab ©)
Both effects combined (greater pressure at the trailing edge and a0l displacement) lead to a lift coefficient variation as seen in Fig. 3.
CONCLUSIONS
The following conclusions may be drawn from the parameterization of the NACA profiles:
Allowing modifications at the trailing edge of NACA profiles influences the behaviour of both lift and drag coefficients. The two most important characteristics are the increase of αl/dmax and the changes of the stall behaviour of the airfoil.
The implications on manufacture of the proposed modifications can be summarized as a simplified construction of the profile, because the trailing edge must not be manufactured to a knife-sharp edge, but imperfections may be allowed.
Although the consequences regarding the manufacture of airfoils are very important, further work is required to determine the benefits that can be achieved by having higher values of b1 and flatter C1/Cd curves. For example, with higher values of b1, the positioning of the profiles in a wind turbine can be made in such a way that higher lift coefficients can be achieved.
Experimental validation of these computational findings is expected to be carried out once the wind tunnel facility of the Universidad de Los Andes becomes operational in 2007.
REFERENCES
[1] D.R. Chapman, R.H.Kester. "Effect of Trailing Edge Thickness at Supersonic Velocities". Ames Aeronautical Laboratory. NACA RM A52D17. Washington. 1952. [ Links ]
[2] J.L Summers, W.A. Page. "Lift And Moment Characteristics at Subsonic Mach Numbers of Four 10 Percent Thick Airfoil Sections of Varying Trailing Edge Thickness". Ames Aeronautical Laboratory. NACA RM A50J09. Washington, 1950. [ Links ]
[3] J. Herrig et. al. "Effect of Section Thickness and Trailing Edge Radius on the Performance of NACA 65- Series Compressor Blades in Cascade at Low Speeds". NASA RM L51J16. 1951. [ Links ]
[4] J.J. Moses, G.K. Serovy. "Some Effects of Blade Trailing Edge Thickness on performance of a Single-Stage Axial Flow Compressor". Lewis Flight Propulsion Laboratory. NACA RM E51E28. Washington, 1951. [ Links ]
[5] E.N. Jacobs, K.E. Ward, R.M Pinkerton. "The Characteristics of 78 Related Airfoil Sections from Tests in the Variable Density Wind Tunnel", NACA report 460, N.A.C.A, 1932. [ Links ]
[6] L. M. Milne Thomson. Theoretical Aerodynamics. New York: Dover Publications, Inc., 1958. [ Links ]
[7] I. H Abbott, A. Doenhoff. Theory of Wing Sections. New York: Dover Publications, Inc., 1959. [ Links ]
[8] E.H. Lysen. "Introduction to Wind Energy". CWD - Consultancy Services Wind Energy Developing Countries. Amersfoort, 1983, [ Links ]
[9] T. Burton et al. Wind Energy: Handbook. New York: John Wiley and Sons, 2001. [ Links ]