Boosting Support Vector Machines

Máquinas de vectores de soporte

Elkin Eduardo García Díaz
Ingeniero Electronico, M.Sc. en Ingenieria Electronica. Profesor Instructor, Departamento de Ingenieria Electrica y Electronica, Universidad de los Andes, Bogota D.C., Colombia.
elkin-ga@uniandes.edu.co

Fernando Lozano Martínez
Ingeniero Electronico, Ph. D. Electrical Engineering. Profesor Asistente, Departamento de Ingenieria Electrica y Electronica, Universidad de los Andes, Bogota D.C., Colombia.
flozano@uniandes.edu.co

Recibido 13 de marzo de 2006, aprobado 7 de noviembre de 2006.

PALABRAS CLAVE
Boosting, generalizacion, SMO, SVM.

RESUMEN
En este articulo, se presenta un algoritmo de clasificacion binaria basado en Support Vector Machines (Maquinas de Vectores de Soporte) que combinado apropiadamente con tecnicas de Boosting consigue un mejor desempeno en cuanto a tiempo de entrenamiento y conserva caracteristicas similares de generalizacion con un modelo de igual complejidad pero de representacion mas compacta.

KEYWORDS
Boosting, generalization, SMO, SVM.

ABSTRACT
In this paper we present an algorithm of binary classification based on Support Vector Machines. It is combined with a modified Boosting algorithm. It run faster than the original SVM algorithm with a similar generalization error and equal complexity model but it has more compact representation.

INTRODUCCION

Las máquinas de vectores de soporte (SVM por sus siglas en inglés) han sido, en los últimos años, una técnica ampliamente aplicada a problemas de clasificación y regresión [1]. Desde el punto de vista de aprendizaje estadístico, una de las razones de su éxito es que para ciertas funciones kernel se ha demostrado que SVM es un aprendiz fuerte [2], es decir que puede alcanzar un error de generalización arbitrariamente cercano al error de Bayes con un conjunto de entrenamiento lo suficientemente grande. La principal desventaja de SVM es la complejidad temporal del algoritmo. Siendo m el número de elementos del conjunto de entrenamiento, SVM resuelve un problema de programación cuadrática que implica inicialmente complejidad O(m³). Múltiples investigaciones han propuesto métodos para mejorar esta complejidad [3] [6] llegando a que sea O(m²).

Por otra parte, algoritmos como Adaboost [7] encuentran una buena hipótesis combinando adecuadamente hipótesis dadas por un aprendiz débil, es decir un algoritmo que retorna una hipótesis cuyo desempeño es mejor que adivinar. Sin embargo, usar un algoritmo fuerte como clasificador base de Adaboost no representa gran ventaja desde el punto de vista de la generalización. Wickramaratna, Holden y Buxton han usado SVM como clasificador base de Adaboost, pero el desempeño del clasificador resultante se degrada con el aumento del número de rondas [8]. Por esta razón puede ser útil hacer de SVM un algoritmo débil para aprovechar las ventajas de Adaboost.

Adicionalmente, el debilitar SVM trae otras ventajas ya que puede utilizarse para reducir el conjunto de entrenamiento con el fin de simplificar la representación de SVM [9], lo que se conoce como algoritmo de editing.

A continuación, en la sección II se revisan los conceptos básicos de clasificación, así como los fundamentos de los algoritmos de Boosting y SVM. La sección III presenta el algoritmo propuesto de Boosting Support Vector Machines (BSVM). La sección IV muestra el análisis de los experimentos realizados y finalmente la sección V presenta las conclusiones.

PRELIMINARES

Sea Ξ un espacio de entrada, Ψ un espacio de etiquetas y Δ una distribución sobre Ξ. Dada una secuencia 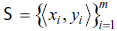= de ejemplos etiquetados donde cada x_i Î Ξ es independiente e idénticamente distribuido de acuerdo a Δ, se asigna cada y_i Î Ψ de acuerdo a una regla posiblemente estocástica. En el caso de clasificación binaria se restringe Ψ = {-1,+1}

Se define una regla de clasificación llamada hipótesis como una función h: Ξ α Ψ que asigna una etiqueta a cada elemento en el espacio de entrada. En el problema de clasificación binaria se tiene que h: Ξ α[-1,+1], donde el signo de h(x) es interpretado como la predicción de la etiqueta a ser asignada a la instancia x, mientras que la magnitud |h(x)| es interpretada como la "confianza" de esta predicción. Adicionalmente una clase de hipótesis Η es un conjunto compuesto por diferentes hipótesis en el espacio de entrada.

El desempeño de una hipótesis será evaluado utilizando el error de generalización R y el error empírico R_emp definidos como:

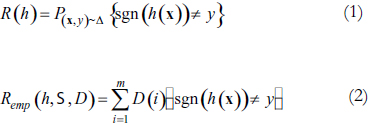
Donde D Î R^m es una distribución discreta sobre el conjunto de muestras etiquetadas y es la función indicadora.

Un algoritmo de aprendizaje es un procedimiento eficiente que toma como entradas un conjunto de muestras etiquetadas ∑ y una distribución discreta D para retornar una hipótesis h Î Η. Un clasificador combinado H(x) es la combinación convexa de varias hipótesis h_i (clasificador base) de tal forma que

A. BOOSTING

Las estrategias de Boosting pretenden elevar el desempeño de un algoritmo de aprendizaje débil combinando varias hipótesis adecuadamente y generando un algoritmo de aprendizaje fuerte. El algoritmo Adaboost [10] o Boosting adaptativo introducido en [11] es un meta-algoritmo (un procedimiento que usa otro procedimiento como subrutina) que toma un conjunto de muestras etiquetadas ∑, una distribución discreta D y un aprendiz débil Weak para retornar un clasificador combinado en T iteraciones. En cada iteración t Adaboost ejecuta Weak sobre el conjunto ∑ con la distribución D_t para obtener la hipótesis h_t. De acuerdo al desempeño de h_t, el algoritmo modifica D_t dándole menor peso a las muestras bien clasificadas y mayor peso a las muestras mal clasificadas con el objetivo que el siguiente clasificador se concentre en estas últimas, maximizando la cantidad de información que obtendrá en la siguiente ronda. La figura 1 muestra este algoritmo como fue presentado en [10].

Fig. 1. Algoritmo Adaboost

B. SUPPORT VECTOR MACHINES

El objetivo de Support Vector Machines en el problema de clasificación binario es encontrar el hiperplano separador óptimo (aquel que maximiza el margen geométrico) en el espacio de características Ξ '. Éste está relacionado con el espacio de entrada Ξ (espacio original de los datos) por medio de una transformación no lineal Φ(x) de altas dimensiones que busca que los datos del conjunto de elementos etiquetados ∑ sean separables. Cuando el conjunto de ejemplos etiquetados no es linealmente separable, el interés es encontrar el hiperplano con el menor error empírico. Sin embargo, el problema de encontrar este clasificador es NP-Hard [12], razón por la cual se pueden descartar algunos puntos con algún margen positivo fijado, en cuyo caso el problema tiene complejidad polinomial.

Cortes y Vapnik [13] [14] proponen resolver el siguiente problema de optimización, formulación conocida como C-SVM

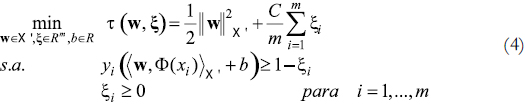
Donde C >0 es una constante que controla el "trade- off" entre minimizar el error de entrenamiento y maximizar el margen. Nótese que cuando ξ_i = 0, no existe un margen de error, sin embargo ξ_i > 0 implica que las clases se traslapan. Adicionalmente, este problema requiere el cálculo de la transformación Φ(x) para todos los datos de entrenamiento y de la minimización de w en el espacio de características. Por estas razones se plantea el problema dual de (4)

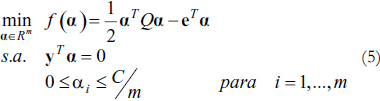
Donde Q_ij = y_iy_jk(x_i, x_j) y e el vector de todos unos, definiendo 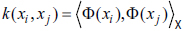como un kernel positivo definido. Adicionalmente la hipótesis está dada por

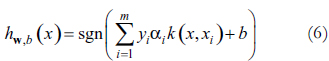
Es de destacar que este hiperplano en el espacio de características X' está en función de los datos de entrenamiento para los que α_i ≠ 0, éstos son los vectores de soporte. Es claro que (5), el problema dual de (4), es un problema de programación cuadrática con restricciones lineales mucho más sencillos de resolver que el original puesto que únicamente está en función de los kernel. Sin embargo, no puede ser fácilmente resuelto por técnicas tradicionales dado que involucra una matriz Hessiana de dimensión m × m. Por esta razón, para resolver (5) han surgido múltiples métodos que buscan ser más eficientes [3] [6] destacándose Secuential Minimal Optimization (SMO) en donde se descompone el problema original de tal forma que sólo se requiere resolver problemas cuadráticos de dos variables de forma analítica. La combinación de SMO con técnicas de shrinking y caching [5] ha permitido que la complejidad computacional en la resolución de (5) esté entre cuadrática y cúbica, dependiendo del tipo de problema y dominada básicamente por el número de evaluaciones que se requieren de la función kernel [15].

BOOSTING SUPPORT VECTOR MACHINES

Debido a que la complejidad de SVM depende intrínsecamente del número de datos de entrenamiento, se busca que en el planteamiento del problema cuadrático intervenga sólo un subconjunto de los datos originales, sin que esto implique que se descarten totalmente. Razón por la cual las estrategias de Boosting son una alternativa para combinar varias hipótesis generadas de esta forma. Adicionalmente, entrenar con una fracción de los datos μm y combinar q hipótesis puede demorar mucho menos tiempo que entrenar con los datos completos, pues si la complejidad del algoritmo original está acotada por Am^x con AÎ R, al entrenar con la fracción μm está acotado por A(μm)^x; y combinando q hipótesis por Aq(μm)^x(despreciando la complejidad del algoritmo que las combina). Con x > 1, 0 > μ > 1 y q ≤ 1/μ se tiene que:

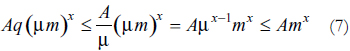
De donde aunque el algoritmo resultante sigue siendo O(m^x), la constante que lo acota es menor.

Por esta razón se busca utilizar SVM como clasificador débil de un algoritmo de Boosting similar a Adaboost, para ello se hace necesario modificar el problema de optimización (5) para tener en cuenta las distribuciones y garantizar que SVM es un algoritmo débil.

A. SUPPORT VECTOR MACHINES PARA DISTRIBUCIONES

Para el caso en el que se tenga una distribución discreta D Î R^m sobre el conjunto de muestras etiquetadas ∑, se hace necesario dar mayor importancia a aquellos datos con mayor peso dentro de la distribución, en otras palabras es más grave tener un bajo margen o un margen negativo para un dato o conjunto de datos con peso considerable que para uno con bajo peso, por esta razón se deben involucrar los valores de las distribuciones en el planteamiento original de C-SVM. Por lo cual se modifica el planteamiento original de SVM en términos de distribuciones penalizando en la función objetivo las variables de holgura ξ_i de forma proporcional al peso del dato x_i de acuerdo a D. De esta forma el planteamiento del problema de optimización y su dual son

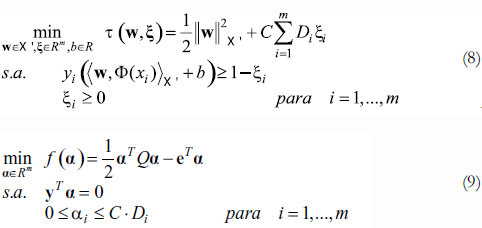
B. SUPPORT VECTOR MACHINES COMO ALGORITMO DEBIL

Debido a la degradación del desempeño que experimentan las técnicas de Boosting con SVM respecto al número de rondas [8], resulta útil debilitarlo para aprovechar las ventajas de Boosting con respecto a la generalización.

Para hacer de SVM un clasificador débil y teniendo en cuenta que la complejidad está entre cuadrática y cúbica respecto al número de datos, es posible despreciar cierta cantidad de datos μ, de tal forma que se resuelva el problema con un porcentaje mucho menor, siempre y cuando con respecto al conjunto total, el error pesado no supere el 50%.

Adicionalmente, los datos que se descarten deben ser los menos representativos del conjunto, es decir los que tengan menos peso en la distribución. De esta forma el subconjunto J Ì ∑ estará definido por ∑_jÎJ D_j ≤ (1 - μ) donde J tiene mínima cardinalidad, presentando como ventaja adicional que el nuevo conjunto de entrenamiento es el más pequeño posible, minimizado al máximo el tiempo de entrenamiento. μ es un parámetro adicional del algoritmo el cual se puede determinar mediante alguna estrategia de selección de modelo.

C. BOOSTING SUPPORT VECTOR MACHINES

Luego de tener un algoritmo debilitado para SVM, se puede aplicar directamente un algoritmo de Boosting como Adaboost, con lo cual la hipótesis final del clasificador combinado de acuerdo a (6) está dada por

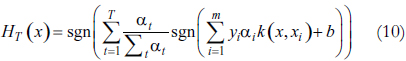
Sin embargo, es claro que no es un hiperplano clasificador en el espacio de características y que la complejidad de la hipótesis H_T(x) es mucho mayor que la de SVM dada por (6) Por esta razón se desea modificar el algoritmo Adaboost de la figura 1 de tal forma que el clasificador combinado también tenga la forma de (6). Este algoritmo denominado BSVM se detalla en la figura 2.

Fig. 2. Algoritmo BSVM

El algoritmo BSVM conserva las características principales de Adaboost. En cada iteración modifica de la misma forma la distribución de los datos; sin embargo, la principal diferencia radica en que, debido a que la hipótesis final es también un hiperplano clasificador en el espacio de características, la forma de hallar los coeficientes α_t de cada hipótesis base se hace planteando un problema de optimización cuyo objetivo es minimizar el error en los datos de entrenamiento de la combinación convexa de la hipótesis actual h_t(x) y la hipótesis combinada de los clasificadores anteriores H(x). Por esta razón el problema de hallar α_t en cada ronda se reduce a un problema de búsqueda de línea con restricciones, de fácil resolución por métodos numéricos como búsqueda dorada o interpolación con la cúbica.

Adicionalmente, puesto que BSVM no aumenta la complejidad del modelo y por esta razón cada vez se hace más difícil encontrar un hiperplano combinado mejor, existe otro criterio de parada diferente al número de rondas, el criterio es α_t = 0 pues esto implica que el error de entrenamiento no mejoró y que la hipótesis resultante H(x) no sufre modificaciones. También lo es R_emp(H(x), ∑, D₁) = 0 pues cuando el error de entrenamiento es cero, no es posible mejorar más.

Teniendo en cuenta que el objetivo de este proceso de entrenamiento es la generalización, no necesariamente el obtener el error más bajo en entrenamiento implica un error bajo de generalización, puesto que se puede presentar sobre ajuste a los datos, por lo cual se hace necesario incluir otros criterios de parada cuyo objetivo sea prevenir esto. Una primera alternativa es utilizar un sistema de parada temprana en donde a partir de un subconjunto de los datos de entrenamiento se verifique y controle cuando existe sobre ajuste y así finalizar el algoritmo. Otra alternativa es utilizar los valores de error de entrenamiento de rondas anteriores para, aprovechando que forman una sucesión descendente, hallar en qué porcentaje se mejoró el error; un porcentaje muy bajo es indicio de sobre ajuste. Con lo cual se puede utilizar

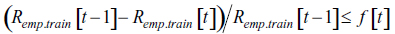
siendo f[t] decreciente o constante. Así mismo los α_τ forman una sucesión, en la mayoría de los casos descendente, y valores muy bajos son prohibitivos para la generalización. De allí que otro criterio de terminación es α_t ≤ g[t] con g[t] decreciente o constante.

EXPERIMENTOS

En esta sección se muestran algunos experimentos de clasificación binaria aplicando el algoritmo BSVM propuesto, utilizando tanto datos artificiales como de problemas reales de diversas características respecto a dimensión y número de datos de entrenamiento y validación.

Para el conjunto de datos MNIST de dígitos manuscritos [16] se toma el problema binario de clasificar las clases 3 y 8 por su alta complejidad, es un conjunto de gran tamaño y de altísimas dimensiones. Fournorm es un problema de clasificación binario de 20 dimensiones en donde los datos de la primera clase provienen con igual probabilidad de dos distribuciones normales con matriz de covarianza identidad y medias en (a,a,...,a) y (-a,-a,...,-a), mientras los datos de la segunda clase provienen con igual probabilidad de dos distribuciones normales con matriz de covarianza identidad y medias en (a,-a,...,a,-a) y (-a,a,...,-a,a) para este caso se toma 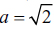, se destaca en este conjunto, adicional a su dimensión, que las clases están bastante superpuestas, razón por la cual el error de Bayes es apreciable, pero a diferencia de un problema real, es calculable teóricamente. Breast cancer, diabetes y australian son tres bases de datos del repositorio de UCI [17]; la primera para identificar si un tumor es benigno o maligno, separable fácilmente, la segunda para diagnosticar diabetes y la tercera para aprobar créditos; este grupo aunque es de menor número de datos respecto a las primeras, los datos son de dimensiones apreciables. En los casos en los que el conjunto no está fraccionado en entrenamiento y validación, se toma el 90% para entrenamiento y el 10% para validación. En todos los experimentos se utilizó un kernel gaussiano k(x_i, x_j) = exp(-||x_i - x_j||²/σ). Las características de las bases de datos y los parámetros del kernel utilizado en cada caso se encuentran en la tabla I.

TABLA I. Características de las bases de Datos y Comparación de SVM y BSVM

Para el algoritmo de SVM con distribuciones se usa la misma filosofía de SMO [6] así como las mejoras propuestas por otros autores [18] [15] haciendo las modificaciones necesarias para resolver (9). Por el amplio número de datos en entrenamiento y validación, se utiliza MNIST para hacer un análisis general del algoritmo. Durante los experimentos se utilizó f[t]=0.25 y g[t]=1/t². Aunque para el entrenamiento no se disminuya tanto el error a medida que se rechazan datos, para la evaluación sí se mejora el desem- peño, disminuyendo el error sobre todo a medida que se rechazan más datos y mejorando la generalización con los criterios de parada aplicados.

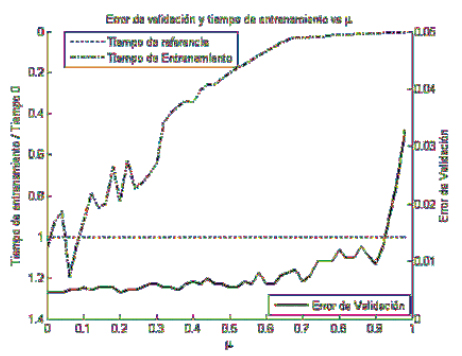
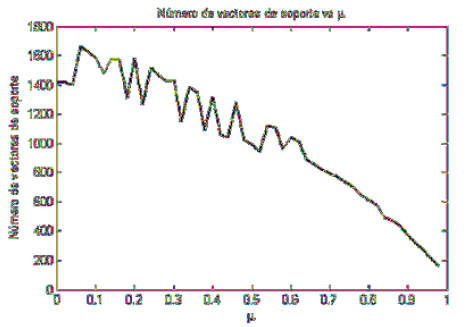
La figura 3 muestra la relación entre el error de validación (sin sobre entrenamiento) y el tiempo de entrenamiento a medida que se rechazan más datos. A pesar que el algoritmo sigue generalizando a valores similares a los del modelo obtenido sin rechazar datos, el tiempo de entrenamiento decrece dramáticamente a valores inferiores a 1/10 del tiempo original. Sin embargo, el modelo no generaliza bien si se desprecian demasiados datos. Respecto al número de vectores de soporte, la figura 4. muestra cómo, aplicando los criterios de parada descritos, a medida que se rechazan más datos el número de vectores de soporte también disminuye independientemente del error de entrenamiento y de evaluación; pero, se destaca que en pruebas preliminares en ausencia de estos criterios el sobre ajuste del modelo también implicaba, en algunos casos, un incremento sustancial en el número de vectores de soporte, lo que puede aprovecharse como un criterio adicional de parada.

Fig. 3. Relación entre el error de validación, el tiempo de entrenamiento y el porcentaje de datos rechazados μ

Fig. 4. Relación entre el número de vectores de soporte y el porcentaje de datos rechazados μ sin sobreentrenamiento

La tabla I. también resume los resultados obtenidos para los diferentes conjuntos probados. De acuerdo a esto hay varios aspectos a destacar. El primero de ellos hace referencia a que en todos los casos BSVM obtuvo con muy pocas rondas un error de generalización similar al del algoritmo original, demostrando la efectividad y rápida convergencia del algoritmo diseñado. Adicionalmente, en la mayoría de los casos lo hace en un tiempo menor, en particular con MNIST y australian, conjuntos con muchos datos y/o altas dimensiones. En relación con el número de vectores de soporte se puede apreciar como BSVM obtiene un número reducido de vectores de soporte, sin comprometer la generalización del modelo, esta reducción es mucho mayor en aquellas clases que son no separables y por lo tanto tienen un error de Bayes apreciable, como es el caso de four-norm o diabetes.

CONCLUSIONES

El algoritmo propuesto BSVM combina eficientemente diversos clasificadores SVM por medio de técnicas de Boosting, sin aumentar la complejidad de la hipótesis resultante y en un tiempo mucho menor, en particular cuando el conjunto de entrenamiento es extenso y/o la dimensión de los datos es alta.

Adicionalmente, con esta implementación los modelos son mucho más compactos puesto que poseen un número menor de vectores de soporte.

Las estrategias propuestas para evitar el sobre ajuste son efectivas, de tal forma que BSVM presenta valores similares en cuanto a generalización respecto a la implementación original.

Quedan planteados como temas de investigación futuros: el hallar cotas teóricas más ajustadas para el porcentaje de datos rechazado y determinar criterios analíticos de parada más precisos.

REFERENCIAS

[1] B. Schölkopf and A. Smola. Learning With Kernels. Cambridge, MA: MIT Press, 2002.        [ Links ]

[2] I. Steinwart. "Cosistency of support vector machines and other regularized kernel classifiers", IEEE Transactions on Information Theory, vol. 51, no. 1, pp. 128-142, January 2005.        [ Links ]

[3] V. Vapnik. Estimation of Dependences Based on Empirical Data. Springer- Verlag, 1982.        [ Links ]

[4] E. Osuna, R. Freund, and F. Girosi. Improved training algorithm for support vector machines. In Proc. IEEE Neural Networks in Signal Processing '97, p p. 276 - 285, 1997.        [ Links ]

[5] T. Joachims. "Making large-scale SVM learning practical" in Advances in Kernel Methods - Support Vector Learning, B. Schölkopf, C. J. C. Burges, and A. J. Smola, Eds. Cambridge, MA: MIT Press, 1999, pp. 169-184.        [ Links ]

[6] J. Platt. "Fast training of support vector machines using sequential minimal optimization", in Advances in Kernel Methods - Support Vector Learning, B. Schölkopf, C. J. C. Burges, and A. J. Smola, Eds. Cambridge, MA: MIT Press, 1999, pp. 185-208.        [ Links ]

[7] Y. Freund and R. Schapire. "A decision-theoretic generalization of online learning and an application to boosting", Journal of Computer and System Sciences, vol. 55, no. 1, pp. 119-139, Aug. 1997.        [ Links ]

[8] J. Wickramaratna, S. Holden, and B. Buxton. "Performance degradation in boosting", in Proceedings of the 2nd International Workshop on Multiple Classifier Systems MCS2001, ser. LNCS, J. Kittler and F. Roli, Eds. Springer, 2001, vol. 2096, pp. 11-21.        [ Links ]

[9] P. Rangel, F. Lozano, E. García. "Boosting of Support Vector Machines with application to editing" in Proceeding of the 4th Int. Conf. of Machine Learning and Applications ICMLA´'05, Dec. 2005.        [ Links ]

[10] R. Schapire and Y. Singer. "Improved boosting algorithms using confidence-rated predictions", Machine Learning, vol. 37, no. 3, pp. 297-336, Dec. 1999. [Online]. Available: http://www.boosting. org/papers/SchSin99b        [ Links ]

[11] Y. Freund and R. E. Schapire. "A decision-theoretic generalization of on-line learning and an application to boosting", Journal of Computer and System Sciences, vol. 55, no. 1, pp. 119-139, Aug. 1997. [Online]. Available: http://www.boosting.org/papers/FreSch97.ps.gz        [ Links ]

[12] D. Johnson and F. Preparata. "The densest hemisphere problem", Theorical Computer Science, no. 6, pp. 93-107, 1978.        [ Links ]

[13] C. Cortes and V. Vapnik. Support-vector network. Machine Learning, 20:273-297, 1995.        [ Links ]