Planeamiento en el largo plazo de un sistema de transmisión de energía eléctrica incluyendo valoración explícita de la confiabilidad

Long Term Planning of a Power Transmission System with Explicit Assessment of The Reliability

Lina Garcés
MSc. Estudiante doctoral, Universidad Estadual Paulista. Ilha Solteira, Brasil.

Carlos J. Zapata
MSc. Profesor de la Universidad Tecnológica de Pereira. Pereira, Colombia.
cjzapata@utp.edu.co

Recibido 25 de septiembre de 2006, aprobado 14 de mayo de 2007

PALABRAS CLAVES
Confiabilidad de sistemas de potencia, planeamiento de sistemas de potencia, algoritmos genéticos, optimización.

RESUMEN

Este artículo presenta el análisis del planeamiento en el largo plazo de un sistema de transmisión de energía eléctrica como un problema de optimización no lineal entero mixto que incluye en la función objetivo el valor esperado de racionamiento de potencia como índice que mide en forma explícita la confiabilidad. Este problema se resuelve combinando las técnicas de algoritmos genéticos para la parte de optimización y la enumeración de estados para la confiabilidad. Como ejemplo real de aplicación se presenta un estudio de expansión del sistema de transmisión que sirve a la ciudad de Pereira en Colombia.

KEYWORDS
Power system reliability, power system planning, genetic algorithms, optimization.

ABSTRACT

This paper presents the long term planning analysis of a power transmission system as a nonlinear integer mixed optimization problem that includes in the objective function the expected power not served as index that explicitly measures the reliability. This problem is solved combining the techniques of genetic algorithms for the optimization part and the state space enumeration for the reliability. As a real example, an expansion study of the power transmission system that serves the city of Pereira in Colombia is presented.

INTRODUCCIÓN

El objetivo del planeamiento en el largo plazo de un sistema de transmisión de energía eléctrica es identificar alternativas de expansión de la infraestructura de transporte que permitan atender la demanda futura cumpliendo unos requisitos básicos de calidad de la potencia, seguridad y confiabilidad con un mínimo costo operativo y de inversión; por esta razón, este análisis también se conoce como planeamiento de la expansión. Matemáticamente, este análisis corresponde a un problema de optimización no lineal entero mixto, cuyos espacio de solución (las alternativas posibles) y espacio de estados operativos en cada alternativa (aquéllos que resultan de la pérdida de los componentes) son de dimensiones combinatoriales; por lo cual, los investigadores han explorado diversas metodologías para obtener la solución óptima o una buena solución sub-óptima en el menor tiempo computacional posible, las cuales se pueden clasificar en tres grupos [1]: métodos empíricos basados en el juicio de ingeniería y criterios determinísticos, los métodos de optimización clásica que usan técnicas de descomposición matemática y las técnicas de optimización combinatorial como algoritmos genéticos, grasp, etc.

Dada la complejidad del problema a resolver, todas las metodologías de solución han realizado grandes simplificaciones en el tratamiento de los aspectos de calidad de la potencia, seguridad y confiabilidad; sólo para mencionar el caso de la confiabilidad, ésta ha sido tradicionalmente abordada mediante el criterio determinístico n-1 el cual no establece índices o medidas que permitan hacer comparaciones cuantitativas entre alternativas o incluirla en análisis económicos. Por esto, actualmente se trabaja tanto en el desarrollo de nuevas metodologías para la búsqueda de soluciones en el menor tiempo posible como en el mejoramiento del análisis del desempeño del sistema, de tal forma que los aspectos de calidad de la potencia, seguridad y confiabilidad sean tratados en forma más rigurosa. Así, en este artículo se aborda la valoración en forma explícita (cuantitativa) de la confiabilidad dentro del problema de optimización correspondiente al planeamiento en el largo plazo de un sistema de transmisión de energía eléctrica.

ESPACIOS DE SOLUCIONES POSIBLES Y DE ESTADOS OPERATIVOS

El espacio de soluciones posibles al problema de planeamiento en el largo plazo de un sistema de transmisión está dado por todas las alternativas de conexión de nuevos elementos (líneas de transmisión y transformadores de potencia) entre los nodos del sistema. Este espacio está acotado por el número máximo permitido de adiciones entre nodos y las acciones plausibles de adición, aquéllas donde es lógico que se puedan adicionar nuevos componentes: por ejemplo, no es posible adicionar una línea de transmisión entre nodos de diferente tensión, sólo es posible conectar un transformador de potencia si los nodos están ubicados en un mismo sitio y, en algunos casos, dadas las condiciones geográficas, no es factible unir con líneas de transmisión ciertos nodos. Para cada una de las alternativas plausibles de expansión, se debe evaluar si en cada uno de los estados operativos posibles (aquellos que resultan de la pérdida de los componentes) el sistema cumple las condiciones de calidad de la potencia, seguridad y confiabilidad. Para una alternativa de expansión con n componentes que sólo existen en los estados disponible e indisponible, habrá 2ⁿ estados operativos posibles, los cuales abarcan contingencias de todo orden (n-1, n-2,..., n-n) tanto en las unidades de generación como los componentes del sistema de transmisión. Como ejemplo, en la Figura 1 se muestra la enorme dimensión que pueden tener tanto el espacio de soluciones posibles como el espacio de estados operativos de cada alternativa de expansión, aún para un sistema de muy pocos nodos y considerando la adición de un solo elemento entre nodos. La alternativa 1 corresponde al sistema actual, es decir, se considera que no se adicionarán nuevos componentes.

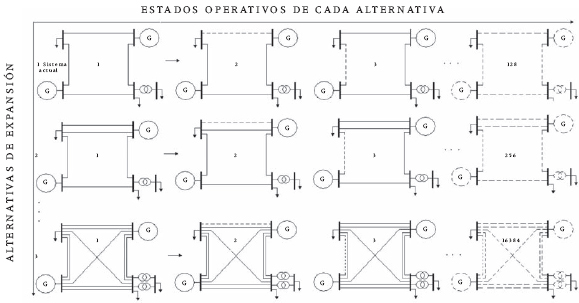
Figura 1. Espacio de soluciones posibles y de estados operativos en un sistema de transmisión.

PLANTEAMIENTO MATEMÁTICO

El problema de planeamiento en el largo plazo de un sistema de transmisión se expresa matemáticamente como:

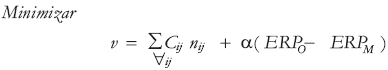
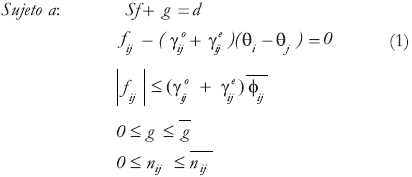
El planteamiento (1) es un problema de optimización no lineal entero mixto clásico de un estudio de expansión de un sistema de transmisión de energía eléctrica al cual se le ha añadido en la función objetivo (n) el ERP para involucrar en forma explícita (cuantitativa, objetiva) la confiabilidad. Dada la alta dimensión de los espacios solución y de estados operativos, el punto central de toda metodología de solución a este problema será el simplificar el análisis de tal manera que, evaluando sólo una parte de estos espacios, se obtenga con poco tiempo computacional una buena solución (solución sub-óptima), no necesariamente el óptimo global. El análisis realizado es estático desde los puntos de vista matemático y eléctrico pues se considera un solo escenario de demanda (una sola etapa en el problema de optimización) y sólo se valora el desempeño eléctrico del sistema para el estado estable de cada estado operativo, sin mirar qué sucede durante las transiciones entre estos estados. Desde el punto de vista de confiabilidad, este análisis se denomina adecuación, pues se valora mediante el índice probabilístico ERP qué tan adecuado es el sistema para atender la demanda futura.

METODOLOGÍA PROPUESTA

Para resolver (1) se combina la técnica de optimización de algoritmos genéticos [2] con la técnica de valoración de confiabilidad de enumeración de estados [3], tal como se muestra en la Figura 2. A continuación se describen brevemente los pasos más importantes de la metodología propuesta; para mayores detalles consultar [4].

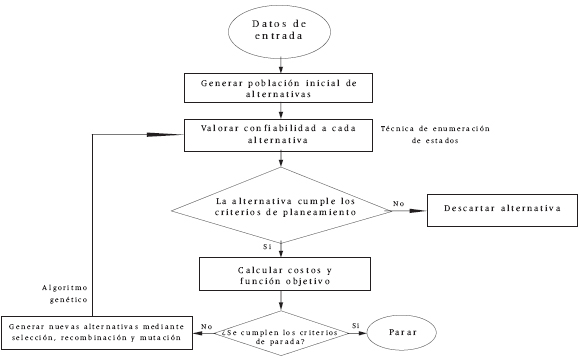
Figura 2. Diagrama de flujo de la metodología propuesta.

SELECCIÓN DE POBLACIÓN INICIAL

Se pueden tomar las alternativas de un plan de expansión de referencia o seleccionar del espacio solución un subconjunto de 50 a 100 alternativas mediante simulación de Montecarlo de eventos equiprobables.

ALGORITMO GENÉTICO

Permite hacer un recorrido rápido al espacio de soluciones posibles. Cada alternativa de expansión se denomina un individuo (filas), cuyos atributos distintivos (columnas) corresponden a los componentes que adiciona de la gama de posibilidades plausibles.

1. Proceso de selección: Consiste en generar descendientes de las alternativas. Se utiliza el método de selección por torneo en el cual se define el número de individuos participantes por juego y el número de descendientes máximo por individuo. El juego se inicia seleccionando aleatoriamente los participantes a los cuales se les calcula la función de adaptación usando una tasa de adaptación (Ta) parámetro cuyos valores típicos oscilan entre 0.96 y 1.1; esto permite realizar discriminación entre los individuos de la población dando mayor valor a los individuos considerados buenos.

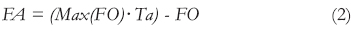
Luego, se asigna un hijo al individuo con mejor función de adaptación, sin exceder el número máximo de hijos permitido. Este procedimiento se repite hasta asignar el total de descendientes a las alternativas. El número de descendientes totales es igual al tamaño de la población inicial.

2. Recombinación: La recombinación consiste en escoger dos alternativas y generar a partir de ellas dos nuevas. Se utiliza un parámetro de control llamado tasa de recombinación (Tr) que determina cuántas de las configuraciones seleccionadas son sometidas a recombinación: este valor oscila entre 0.8 y 1. La recombinación que se realiza es de punto simple, es decir, sólo hay un punto de cruzamiento. En el momento de recombinar se verifica si la función objetivo mejora, para esto se compara la función objetivo de los padres con la de los posibles hijos. Si por lo menos uno de los hijos tiene mejor función objetivo que el peor de los padres, se realiza recombinación, de lo contrario, se genera otro punto de cruzamiento; esta verificación se realiza un número determinado de veces. Si al verificar no se han encontrado mejores descendientes, entonces, no se realiza recombinación.

3. Mutación: Consiste en cambiar los atributos de las alternativas. Existe un parámetro de control llamado tasa de mutación (Tm) que indica la probabilidad de que una posición pueda tener su valor actual modificado, este valor oscila entre el 1% y el 5%. En esta aplicación, la mutación consiste en agregar un componente al corredor en las primeras etapas del proceso y, a medida que este converge, se cambia por el retiro de circuitos. Para establecer la posición a mutar, se generan dos números aleatorios: el primero indica el individuo y el segundo el corredor al cual se le agrega o retira un componente.

VALORACIÓN DE CONFIABILIDAD

Calcula los índices de confiabilidad de una alternativa de expansión dada, analizando únicamente los estados operativos con mayor probabilidad de ocurrencia. Se asume que cada uno de los componentes solo existe en dos estados operativos: disponible e indisponible y que todos los componentes son independientes entre sí. El cálculo de un índice de confiabilidad dado I se hace de la siguiente manera:

Donde: P_j es la probabilidad de ocurrencia del estado operativo j, I_j es el valor del índice de confiabilidad I en el estado operativo j y N_x es el número de estados operativos de interés y corresponde a la dimensión del espacio de estados operativos truncado. El índice I corresponde a un valor esperado. En este estudio, además del ERP también se calculan el valor esperado de energía no suministrada (EENS) y la probabilidad de corte de carga (LOLP). El procedimiento de cálculo es el siguiente:

1. Calcule P_j la probabilidad de ocurrencia de cada uno de los estados operativos de la alternativa de expansión bajo estudio. Esta probabilidad se calcula como el producto disponibilidades (A) e indisponibilidades (U) individuales de cada uno de los componentes según el estado operativo que se asume que tienen en cada estado operativo j. Las disponibilidades e indisponibilidades de los componentes se obtienen de estadísticas operativas o de los modelos probabilísticos de dos estados.

2. Ordenar los estados operativos en orden descendente según la magnitud de su correspondiente P_j y seleccionar aquellos con mayor probabilidad de ocurrencia, con lo cual se define N_x. Para esto se recomienda dos criterios: el primero, seleccionar los estados para los cuales P_j ³ 10%, y el segundo, seleccionar aquellos para los cuales åP_j » 80% a 90%. La experiencia muestra que, en general, cumplen estos criterios la mayoría de los estados operativos correspondientes a las contingencias n-1 y unos pocos correspondientes a las contingencias n-2. Por esta razón, en la práctica, el espacio de estados operativos se trunca y se elimina unas pocas contingencias n-1, una gran parte de las n-2 y todas las de orden mayor.

3. Para cada estado operativo seleccionado j realizar un flujo de carga DC y observar sí hay sobrecargas en los componentes; de ser así realizar cortes de carga hasta eliminarlas. Para cada punto de carga k guardar el valor de potencia cortada o racionada PNS_kj. Para cada estado j guardar el tiempo medio de reparación (MTTR_i) de cada componente i que se considera indisponible. El MTTR de un componente se obtiene de estadísticas operativas o de su modelo probabilístico de dos estados.

4. Calcular los índices ERP, EENS para contingencias n-1 y n-2, la probabilidad de pérdida de carga (LOLP) de los puntos de carga y ERP y EENS del sistema:

Donde, PNS^n-2 es la potencia cortada cuando los dos componentes están indisponibles y PNS^n-1 es la potencia cortada cuando uno de los componentes ha sido reparado y el otro permanece indisponible. MTTR₁ y MTTR₂ son los tiempos de reparación de los dos componentes que salen de servicio. L=(D_máxima - P_cortada). Como modelo de la demanda, se utiliza la función de distribución de probabilidad derivada de la curva de carga diaria [3], [5]. El último término de (6) se calcula de la distribución de probabilidad del tiempo de reparación del componente que sale de servicio. Los índices ERP y EENS del sistema se obtienen sumando los respectivos índices de confiabilidad de los puntos de carga.

CRITERIO DE PARADA

Después de realizados un número determinado de iteraciones, el mejor individuo de la ultima población obtenida se considera como la mejor solución obtenida al problema.

EJEMPLO

Como sistema de prueba se utiliza el sistema compuesto generación – transmisión que sirve a la ciudad de Pereira, el cual se muestra en la Figura 3. Los datos eléctricos y de confiabilidad de los componentes de este sistema se presentan en [6] y [7]. Este sistema atiende a aproximadamente 115000 usuarios y tiene una demanda máxima pronosticada de 106 MW para el año 2006. El planeamiento en el largo plazo se realiza para un año futuro donde el pronóstico de demanda máxima es de 250 MW. Para propósitos de comparación se realizan los dos siguientes estudios:

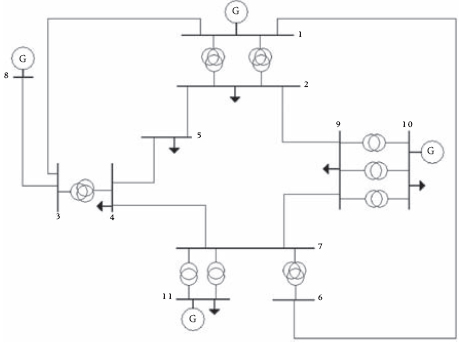
Figura 3. Sistema de prueba.

I. Estudio de expansión sin considerar análisis explícito de confiabilidad utilizando el método GRASP, el cual sólo adiciona componentes hasta que no hayan cortes de carga en el sistema para la demanda pronosticada. A la solución obtenida se le hace un análisis a-posteriori de confiabilidad mediante la técnica de enumeración de estados, para calcular los índices de confiabilidad del sistema y de los puntos de carga.

II. Estudio de expansión que considera el análisis de confiabilidad y utiliza la metodología propuesta. Como criterio de planeamiento se fija un valor máximo permitido para ERP de 5 MW (2%). El número máximo de iteraciones se fijó en 500, a 1000, Ta =1.1, Tr =0.9, Tm =5%. La población inicial se fija en 50 individuos y la selección por torneo se realiza considerando 3 jugadores por juego con un máximo de 3 hijos por jugador.

En las tablas 1 y 2 se presentan los resultados para los puntos de carga y globales del sistema. En la valoración de confiabilidad se consideran 74 estados operativos que representan una probabilidad acumulada del 80%.

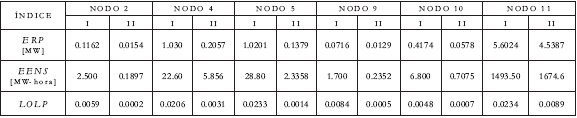
Tabla 1. Índices de confiabilidad de los puntos de carga.

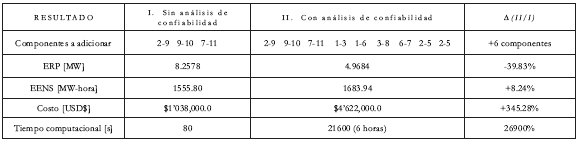
Tabla 2. Resultados globales del estudio de expansión.

CONCLUSIONES Y RECOMENDACIONES

El análisis de planeamiento en el largo plazo de un sistema de transmisión que considera en forma explícita (cuantitativa, objetiva) la confiabilidad, resulta en un requerimiento de componentes y de costo mayor a la solución donde este aspecto se aborda en forma implícita (cualitativa, subjetiva). Esto se debe al hecho de que el análisis simplificado no verifica el cumplimiento de los requisitos básicos de calidad de la potencia, seguridad y confiabilidad para todos los estados operativos que tienen una alta probabilidad de ocurrencia. Al incluir en el análisis de planeamiento de expansión en el largo plazo de un sistema de transmisión la valoración en forma explícita de la confiabilidad, se requiere un mayor tiempo computacional; pero en contraprestación se tienen índices cuantitativos que permiten medir en forma objetiva la confiabilidad tanto del sistema como de los puntos de carga.

Con la metodología propuesta se comprueba que es posible incorporar en forma explícita la valoración de confiabilidad dentro del problema de optimización correspondiente al planeamiento de largo plazo de un sistema de transmisión. Sin embargo, lo aquí presentado es sólo un ejemplo de cómo combinar estos análisis sin pretender que ésta sea la mejor alternativa, por lo cual, se recomienda continuar en el desarrollo de metodologías que combinen otras técnicas de optimización y de valoración de confiabilidad, incorporando el flujo de carga AC para mejorar el análisis del desempeño eléctrico del sistema y reducir el tiempo computacional requerido.

REFERENCIAS

[1] R. Gallego, A. Escobar, R. Romero y A. Monticelli. Planeamiento de la expansión de sistemas de transmisión de energía eléctrica. Pereira: Universidad Tecnológica de Pereira, 2002.        [ Links ]

[2] A. Escobar. Pl aneamiento dinámico de la expansión de sistemas de transmisión usando algoritmos combinatoriales. Tesis de Maestría. Pereira: Universidad Tecnológica de Pereira, 2002.        [ Links ]

[3] C. J. Zapata. Confiabilidad de sistemas eléctricos. Pereira, Universidad Tecnológica de Pereira, 2005.        [ Links ]

[4] L. P. Garcés. Planeamiento de la expansión de la transmisión a largo plazo basado en confiabilidad. Tesis de Maestría. Pereira: Universidad Tecnológica de Pereira, 2005.        [ Links ]

[5] R. Billinton y R. Allan. Reliability Evaluation of Power Systems. Plenum Press, 1996.        [ Links ]

[6] C. J Zapata, L. P Garcés, O. Gómez. “Modelamiento de componentes en sistemas compuestos generación – transmisión para estudios de confiabilidad”. Revista Scientia et Technica, No. 28, 2004. Disponible en: www.utp.edu.co/ciencia        [ Links ]

[7] L. P. Garcés y O. Gómez. Análisis de confiabilidad del sistema de transmisión regional usando simulación de Montecarlo. Proyecto de Grado. Universidad Tecnológica de Pereira, 2003.        [ Links ]

BIBLIOGRAFÍA

Binato, S., G. De Oliveira, J. De Araujo. “A greedy randomized adaptive search procedure for transmission expansion planning”. IEEE Trans. on Power Systems, Vol. 16, No. 2, 2001.        [ Links ]

CIGRE Working Group. Power system reliability analysis - Application guide, 1987.        [ Links ]

CIGRE Task Force. Methods and techniques for reliability assessment of interconnected systems, 1998.        [ Links ]

CIGRE Working Group. Network planning in a deregulated environment, 2003.        [ Links ]

CIGRE Task Force. Techniques for power system planning under uncertainties, 2000.        [ Links ]

Chowdhury A. y D. Koval. “Application of customer interruption costs in transmission network reliability planning”. IEEE Trans. on Industry Applications, Vol. 37, No. 6, 2001.        [ Links ]

Shahidehpour M. “Operational Reliability: Objective or constraint?”. IEEE Power Engineering Society Summer Meeting, 2002.        [ Links ]