Self-Tuning Control for a Class of Bilinear Systems

Controladores auto-ajustables para una clase de sistemas bilineales

Anna Patete
Ph .D. Advanced Multidisciplinary Engineering. Assistant Professor, Universidad de Los Andes. Mérida, Venezuela. apatete@ula.ve

Miguel Ríos
Ph.D. Full Professor, Universidad de Los Andes. Mérida, Venezuela. riosm@ula.ve

Claudia Gómez
Ph.D. Associate Professor, Universidad de Los Andes. Mérida, Venezuela. claudiag@ula.ve

Katsuhisa Furuta
Ph.D. in Engineering. Professor Emeritus, Department of Robotic and Mechatronics, Japan Tokyo Denki University. Tokyo, Japan. furuta@fr.dendai.ac.jp

Recibido 28 de octubre de 2009, modificado 17 de mayo de 2011, aprobada 23 de mayo de 2011.

KEY WORDS

Bilinear systems, generalized minimum variance, selftuning control.

ABSTRACT

In this paper, a self-tuning algorithm based on the generalized minimum variance criterion is proposed for the stabilization of a class of bilinear systems. Using a Lyapunov function and the sliding mode control approach, the stability of the proposed algorithm is proven. The proposed self-tuning algorithm is applied to a simulated example to evaluate its performance.

PALABRAS CLAVES

Sistemas bilineales, controlador auto-ajustable, varianza mínima generalizada.

RESUMEN

En este trabajo, se propone un algoritmo autoajustable implícito basado en el criterio de varianza mínima generalizada para la estabilización de una clase de sistemas bilineales. La estabilidad del algoritmo propuesto es demostrada usando una función de Lyapunov y la estrategia de control por superficie deslizante. El algoritmo auto-ajustable propuesto es aplicado a una planta piloto térmica para evaluar su desempeño.

INTRODUCTION

Bilinear systems comprise perhaps the simplest class of nonlinear systems which has a lot of applications in various fields, e.g. [1] and reference therein. Several control approaches have been proposed to treat the stabilization problem of bilinear systems (see [2, 3] and the references therein). However, only a few papers (e.g. [4, 5]) have focused on the stabilization problem of bilinear systems with time delay. So far, stability of implicit self-tuning control, based on generalized minimum variance criterion for minimum and a class of non-minimum phase linear systems has been demonstrated by the use of a Lyapunov function in [6], and for those systems, it suffices to use linear functions of the data to predict the system output response. However, in general, it may be desirable, or even necessary, to consider the use of nonlinear functions to get good predictions and hence good control performance.

By following the idea of Goodwin [7, 8], Sun [5] gave proof of the explicit self-tuning controller of bilinear systems. However, the proof relies on assuring parameter convergence in the close-loop system, when the projection algorithm is used.

In this paper, stability of the implicit self-tuning controllers for a special class of discrete-time bilinear systems, represented by the input-output relation with unknown parameters, is proven. The treated bilinear class is the class where only bilinearity exists between the measured and the control signals; additionally control signals must appear in the system structure in linear form. The proposed algorithm consists in the combination of the generalized minimum variance control and recursive identification of the control parameters. The control objective is to minimize the variance of a sliding mode surface proposed for this class of bilinear systems. The discretetime bilinear model could be given directly in the discrete- time form or derived by discretization from the continuous-time (minimum or non-minimum phase) system. Stability of the algorithm is proven by using a Lyapunov function. The proposed self-tuning algorithm is applied to a simulated example to verify and to show the performance of the algorithm. Part of this work was presented in the CLCA 2008 [9].

The paper is organized as follows: firstly, the generalized minimum variance criterion for bilinear systems is given. Secondly, the recursive self-tuning controller parameter estimation, based on the generalized minimum variance criterion for the class of bilinear systems, is studied and the main results are given by the theorem which assures overall system stability. Then, the proposed algorithm is applied to a simulated example and digital simulations are shown. The paper concludes with some additional remarks.

GENERALIZED MINIMUM VARIANCE CONTROL FOR BILINEAR SYSTEMS

Bilinear systems are a special class of non-linear systems that are linear in input and linear in state but not jointly linear in state and input. Specifically, a time invariant single-input and single-output (SISO) bilinear system has a discrete-time form as follows:

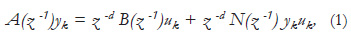
where there are no common factors in (A(z^-1), N(z^-1)), or in (A(z^-1), B(z^-1)) and the time delay d is known. z denotes the time shift operator z^-ty_k= y_k-t. In the Laplace transformation, z = e^sT_o where T_o is the sampling period (for simplicity, and without loss of generality, T_o = 1 is assumed).

In this section, to derive the nominal control law, the polynomials A(z^-1), B(z^-1) and N(z^-1) are assumed to be known, and represented as:

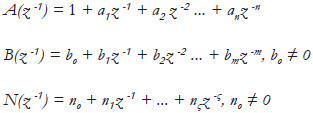
Remark 1: The special class of discrete-time bilinear systems to be considered in this paper is the class where the discrete-time system can be described as in (1).

This means that polynomials A(z^-1) ≠ 0, B(z^-1) ≠ 0, N(z^-1) ≠ 0, d > 0, and the bilinearity is considered only between the output (measured state) and the input variable.

The following notations are introduced:

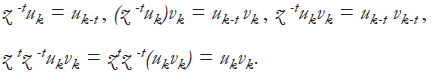
The control objective is to minimize the variance of the controlled sliding mode variable s_k+d, which is defined in the deterministic case as:

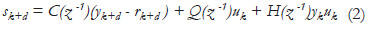
where H(z^-1) = E(z^-1)N(z^-1), and polynomial E(z^-1) will be defined later. The polynomials: C(z^-1) = 1 + c₁z^-1+ c₂z^-2 + ... c_nz^-n, and Q(z^-1) = q_o(1 - z^-1) are to be designed, so that the specification given below should be satisfied. The error signal e_k is defined as e_k= y_k - r_k, where r_k is the reference signal. The proposed idea is similar to that of the discrete time sliding mode control in [10, 11].

Multiplying (1) by E(z^-1), the following is obtained:

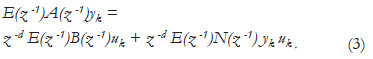
Using the Diophantine equation:

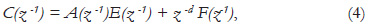
where,

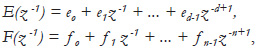
equation (3) is rewritten as:

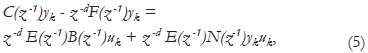
and rewriting (5) in the time k+d, then

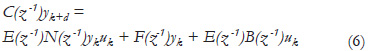
Combining (6) and (2), the sliding mode variable results in:

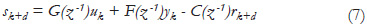
where the polynomial G(z^-1) is defined as:

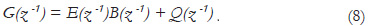
Then the generalized minimum variance control input required to vanish s_k+d in (2) is given by:

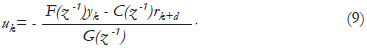
In closed-loop, the characteristic polynomial from the output signal y_k to the reference signal r_k is given by:

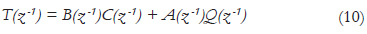
For the closed-loop design, polynomial C(z^-1) must be chosen Schur (all roots of C(z^-1) must be inside the unit disk) and the gain q₀ in Q(z^-1) is designed as any q₀ > 0 that makes the nominal control system stable, the root-locus technique may be used to choose q₀ [6].

SELF-TUNING CONTROL OF BILINEAR SYSTEMS BASED ON GENERALIZED MINIMUM VARIANCE CRITERION

In this section, the system in (1) is considered as a system with the same structure having parametric uncertainties.

The overall stability of the self-tuning control based on generalized minimum variance criterion for SISO linear systems has been proved in [6], when the system constant parameters are not accurately known, by recursive estimation of the controller parameter F(z^-1) and G(z^-1), i.e. F(z^-1) and G(z^-1) are estimates of F(z^-1) and G(z^-1), under the following assumptions [6].

Assumptions 1 [6]: 1. The order of the system (1) is known. 2. The delay step d is known. 3. Polynomial C(z^-1) is Schur. 4. The considered system (1) with parametric uncertainties is in the class of systems which can be stabilized by the polynomials Q(z^-1) and C(z^-1) designed for the nominal system model. 5. The reference signal r_k is bounded, i.e. | r_k |< m_r for all k, where m_r is a positive constant.

Assumption 4 comes from the algorithm´s robust stability analysis explained in [6], and the robust stability is achieved by designing Q(z^-1) and C(z^-1) as explained before.

In this paper, for the bilinear case, the overall stability of self-tuning control for bilinear systems based on generalized minimum variance criterion is given by the following recursive estimation equations:

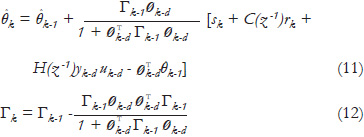
where

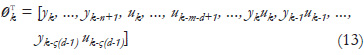
is the vector containing measured output and control signal data,

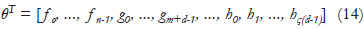
is the vector containing the controller parameters, and

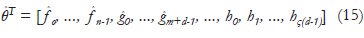
is the estimate of θ. Note that the parameters of H(z^-1) do not need to be estimated. The controller uses identified parameters as follows:

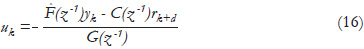
Theorem 1: (Recursive estimates of controller parameters based on generalized minimum variance criterion for bilinear systems.) Given a positive definite matrix Γ₀ and the initial parameters vector θ₀, if the estimate θ_k of the controller (15) satisfies the recursive equations (11) and (12), under the set of Assumptions 1, then the self-tuning controller combining (16), (11) and (12) for the bilinear system (1) with parametric uncertainties is stable.

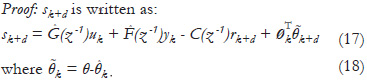
Using the control law (16), equation (17) is rewritten as:

Consider the candidate Lyapunov function:

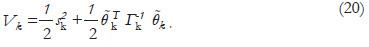
The time difference of (20) is:

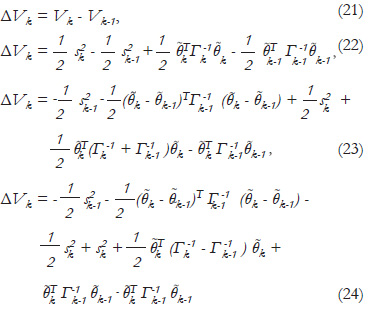
From (19), s_k is:

Substituting (25) into (24), the following relation is derived:

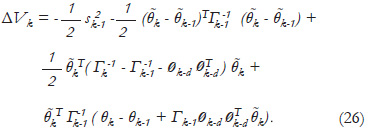
The term:

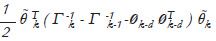
in (24) can be made equal to zero as follows:

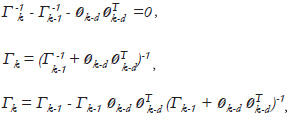
And this yields (12) by the matrix inversion lemma. The term:

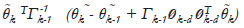
in (26) also can be made equal to zero as described below:

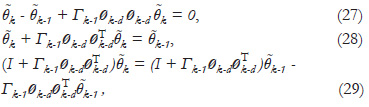
and using (18), then:

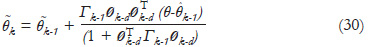
From (8):

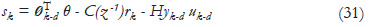
thus (11) is derived. Using the recursive equations (11) and (12) in (26), for k = 1, the following relation is obtained:

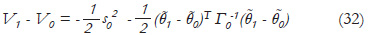
Initially θ₁ - θ₀ ≠ θ, then V₁ - V₀ < 0 which means that V₁ < V₀. For k = 2

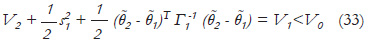
Then, for k=N, where N is large, the following relation is derived:

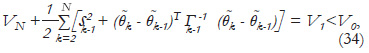
Equation (34) implies that s_N and (θ_N - θ_-1) vanish as N approaches infinity, thus ΔV_k is negative semi-definite for all k and the generalized minimum variance is minimized, which proves the overall system stability. Signal Boundedness: the actual signals y_k, u_k and e_k are shown to be bounded as follows, multiplying (2) by B(z^-1):

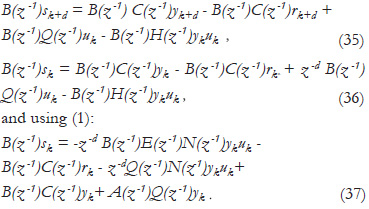
Then, from (8):

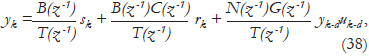
where T(z^-1) is defined as in (10): The signal s_k was proven to go to zero as k→∞. The signal r_k is assumed to be bounded for all k and the signal y_k-d u_k-d was proven to be bounded from the boundeness of vector ø_k^T. From the set of Assumptions 1, number 4 means that the closed-loop characteristic polynomial, considering the described plant with parametric uncertainties, in (1), T(z^-1), is Schur. Thus, y_k in closed-loop is proven to be bounded.

Similarly for u_k, multiplying (2) by A(z^-1), it is obtained that:

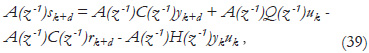
and by using (1):

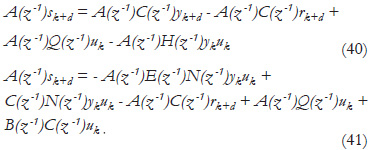
Then, from (4):

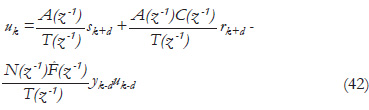
Thus, u_k is proven to be bounded. Using (2), when k→∞ and s_k-d→0, the error is derived:

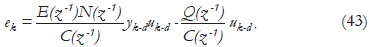
Because C(z^-1) was designed as a Schur polynomial, as k→∞ the signal e_k is bounded for all k. Especially when the signals u_k-d and y_k-d u_k-d become constant, the the error converges to zero to zero, i.e. e_k→0.

SIMULATED EXAMPLE

In this section, a simulated example is presented to support the obtained theoretical results. A discrete-ti-

me non-minimum phase plant with parametric uncertainties is considered. The plant model is known as:

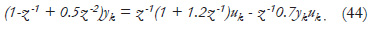
For the control design, the following polynomials are chosen: C(z^-1) = 1+1.18z^-1+ 0.0045z^-2 and Q(z^-1) = 0.1(1 - z^-1).

Using (44), (4) and (8) the following polynomials for the nominal control law (9) are obtained: F(z^-1) = 1.18 - 0.4955z^-1 and G(z^-1) = 1.1 + 1.1z^-1.

Polynomials F(z^-1) and G(z^-1) give the initial estimates F(z^-1) and G(z^-1) for the proposed self-tuning algorithm. For the simulation, the perturbed plant is considered as:

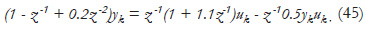
Fig. 1 (a) shows the output response y_k of the system (45), when the nominal controller is used. In Fig. 1 (b) the proposed self-tuning algorithm is used, initial condition for Γ is set to the identity matrix. Fig. 1 (c) and Fig. 1 (d) show the control law u_k and the sliding mode variable s_k. The reference signal r_k is chosen as a sequence of unit-steps with a length of 100 samples.

The simulations show that the proposed self-tuning control algorithm is able to make the output signal follow the reference signal even though there are parametric uncertainties in the system.

Figure 1

CONCLUSIONS

This paper considered the self-tuning control of a class of bilinear systems with constant but unknown parameters. The analysis has been limited to singleinput single-output systems. The overall stability of the proposed self-tuning control algorithm for a class of bilinear systems was proven. The validity of the proposed algorithm was demonstrated through a simulated example.

For future research, the structure of the system will be enhanced to a class of bilinear systems having the presence of a non homog eneous term.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to the revision team for their time, collaboration and comments. These always help us to improve and to think about new lines of research.

REFERENCES

[1] R.R. Mohler. Nonlinear systems: Application to bilinear control. Prentice-Hall. Englewood Cliffs, New Jersey: 1991.        [ Links ]

[2] J.P. Gauthier and I. Kupka. "A Separation Principle For Bilinear Systems With Dissipative Drift". IEEE transactions on Automatic Control, Vol. AC-37, 1992, pp. 1970-1974.        [ Links ]

[3] T. Bose and K.S. Joo. "The Generalized Bilinear System: A Class of Nonlinear Discrete Systems". Proc. of the IEEE International Symposium on Circuits and Systems, Vol. 2, 1994, pp. 185-188.        [ Links ]

[4] Z. Wang, H. Qiao and K.J. Burnham. "On Stabilization of Bilinear Uncertain Time-Delay Stochastic Systems With Markovian Jumping Parameters". IEEE Transactions on Automatic Control, Vol. AC-47, No. 4, 2002, pp. 640-646.        [ Links ]

[5] X. Sun, Y. Jin and C.Z. Fang. "One-Step-Ahead Adaptive Control of Bilinear Systems and Its Application". Proc. of the IEEE International Symposium on Industrial Electronics, 1992, pp. 131-135.        [ Links ]

[6] A. Patete, K. Furuta and M. Tomizuka. "Stability of Self-Tuning Control Based on Lyapunov Function". International Journal of Adaptive Control and Signal Processing, Vol. 22, No. 8, 2008, pp. 795-810.        [ Links ]

[7] G. Goodwin, P. Ramadge and P. Caines. "Discrete-Time Multivariable Adaptive Control". IEEE Transactions on Automatic Control. Vol. 25, No. 3, 1980, pp. 449-456.        [ Links ]

[8] G. Goodwin and K. Sin. "Adaptive Control of NonMinimum Phase Systems". IEEE Transactions on Automatic Control, Vol. 26, No. 2, 1981, pp. 478-483.        [ Links ]

[9] A. Patete, K. Fur uta and M. Rios. "Self-Tuning of Bilinear Systems Based on Generalized Minimum Variance Criterion". XIII Congreso Latinoamericano de Control Automático (CLCA) y VI Congreso Venezolano de Automatización y Control (CAC 2008) . 2008, pp. 557-562.        [ Links ]

[10] K. Furuta. "VSS Type Self-Tuning Control". IEEE, Trans. Ind. Electron., Vol. 40, No. 4, 1993, pp. 7-44.        [ Links ]

[11] K. Furuta. "Sliding Mode Control of a Discrete System". Systems & Control Letters, Vol. 14, 1990, pp. 145-152.        [ Links ]