Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista de Ingeniería
versão impressa ISSN 0121-4993
rev.ing. no.38 Bogotá jan./jun. 2013
Optimal Design of Multilayer EMAs for Frequencies between 0.85 GHz and 5.4 GHz
Diseño óptimo de absorbedores electromagnéticos multicapa para frecuencias en el rango de 0,85 - 5,4 GHz
Iván Amaya(1), Rodrigo Correa(2).
(1) Ph.D (c) on Engineering, Universidad Industrial de Santander, Bucaramanga, Colombia. iamaya2@gmail.com
(2) Ph.D. on Polymer Science and Engineering. Professor, Universidad Industrial de Santander, Bucaramanga, Colombia. crcorrea@uis.edu.co
Received April 12th, 2012, approved April 2nd, 2013.
KEY WORDS
Electromagnetic wave absorber, reflection coefficient, particle swarm, optimization.
ABSTRACT
This article shows some results related to the optimum design of a multilayered electromagnetic absorber, in the frequency range between 0.85 GHz and 5.4 GHz, which belongs to wireless communications. For this design, the Unified Particle Swarm Optimization (UPSO) metaheuristic was used. The results agree with those previously obtained using the standard Particle Swarm Optimization (PSO) algorithm and the deterministic method of interval analysis, which were previously reported. An important reduction on computation time was achieved, although a limited results reproducibility persists.
PALABRAS CLAVES
Absorbedor electromagnético, coeficiente de reflexión, enjambre de partículas, optimización.
RESUMEN
En el presente artículo se muestran algunos resultados relacionados con el diseño óptimo de un absorbedor electromagnético multicapa dentro del rango de frecuencias 0,85 GHz a 5,4 GHz, correspondiente a las comunicaciones inalámbricas. Para este diseño, se utilizó el algoritmo meta-heurístico de enjambre de partículas unificado (UPSO). Sus resultados concuerdan bastante bien con los obtenidos utilizando el algoritmo estándar de enjambre de partículas (PSO) y el método determinístico de análisis de intervalos, previamente reportados. Se destaca la notoria disminución de tiempo de computación, aunque persiste una reproducibilidad limitada de los resultados.
INTRODUCCIÓN
Today, most electronic devices, especially those used for wireless communications, must comply with electromagnetic compatibility standards. This is evaluated in an anechoic chamber, where electromagnetic radiation is measured to test whether it falls below the maximum allowed (Cui, Weile, & Volakis, 2006; Cui & Weile, 2005; Salazar & Mora, 2011). In a similar fashion, the device must also behave properly under the effect of external electromagnetic fields. An alternative test that fulfills both requirements is to use electromagnetic absorbers (EMAs). Recently, interest in this area has increased significantly, due to the growing number of Wi-Fi and Bluetooth capable devices. Another interesting area is socalled EM invisibility at given frequencies, involving new materials and combinations as well as different geometries and textures. Conceptually, EMA are passive elements used (ideally) to attenuate all incident energy. Among the commonest geometries, pyramidal, multilayered and differenttexture multilayered, are the most important (Chamaani, Mirtaheri, Teshnehlab, & Shooredeli, 2007; Liu, Zhang, Gao, Shen, & Shi, 2009; Michielssen, Sajer, Ranjithan, & Mittra, 1993). Optimum design of a device of this kind not only requires it to function properly, but also to take into account electromagnetic, economic and aesthetic variables. Therefore, optimization has migrated from deterministic methods, to evolutionary and metaheuristic ones, such as PSO. Asi et al. designed a multilayer microwave broadband absorber by using Central Force Optimization (another metaheuristic technique, though deterministic in this case), finding that it provided similar results to those achieved using other evolutionary algorithms (M.J. & N.I., 2010).This article presents the design of a planar, three-layer, EMA for the range 0.85 GHz - 5.4 GHz, using Unified PSO (UPSO). The results are compared with those previously reported in [3], using conventional PSO and interval analysis.
FUNDAMENTALS
REFLECTION COEFFICIENT
An EMA is a passive device used to dissipate most of its incident energy. Its main performance parameter is the reflection coefficient, Г, which depends on the permeability (μ) and the permittivity (Є) of the base materials, as well as their order.
A general scheme for a multilayer EMA, is shown in Fig. 1. Each of the N layers is built with a given material, with specific dielectric properties, such as permittivity ( Єk) and permeability ( μk ). The final layer is assumed to be in direct contact with a perfectly conducting wall. It is also assumed that the incident wave is perpendicular to the material. For some cases, this assumption is not too far from reality, e.g. in a cavity inside a cell phone, where the material is placed to keep electromagnetic waves, at a given frequency, from entering or exiting the device.
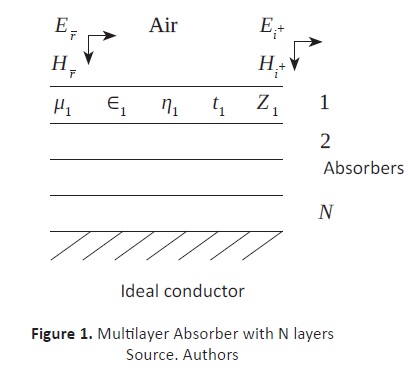
Beginning with the foundations of electromagnetism, the reflection coefficient can be easily shown to be:

where Er / Ei is the relation between the reflected and incident harmonic electric fields. The wave is assumed to be traveling along the z-axis, being γ the complex propagation constant. The total impedance of the absorber Z(z), is defined as the relation between its electric and magnetic fields. Considering this, it can be established that:

where η is the intrinsic impedance. On the other hand, starting from the definition of a material's total impedance, for each one of the N layers, in a lossless medium, it can be shown that (Bronwell, 1944)
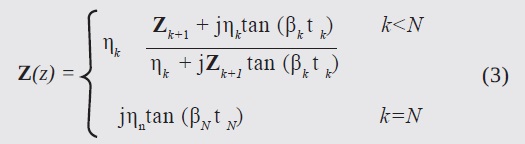
where tk is the thickness of the layer k and ηk is the impedance of the wave at such a layer. The impedance of the last material (from top to bottom), i.e. for k= N shows it to be close to a perfect conductor. βk is the phase constant of the k-th layer; it is a function of the frequency, ƒ which can be defined as:

Building from these concepts, the objective function, for an optimum EMA, can be constructed. Since the reflection coefficient is a direct indicator of efficiency, it is expected to appear in the equation. The total field impedance Z(z) in (2) transforms into the impedance of material 1, which is a function of the inner layers. The intrinsic impedance, η, is that of air, which can be taken to represent the vacuum. Therefore, the equation can be rewritten as:

Given these conditions, it is established that the design requires a previously defined frequency band. Thus, the objective function becomes (Chamaani et al., 2007; Cui & Weile, 2005):
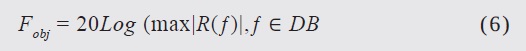
where DB is the design band (i.e. the group of frequencies between 0.85 GHz and 5.4 GHz). Since both the thickness and electromagnetic properties of each layer are unknowns, designing an N layer absorber requires 2N optimization parameters. This is, then, a non-linear multivariable optimization, which simultaneously involves both continuous (e.g. thickness and frequency) and discrete (e.g. type of material) variables. The idea of using this objective function is to minimize the reflection coefficient, thus designing a low weight EMA, which absorbs the maximum amount of perpendicular EM energy. The optimization strategy focuses on selecting the best material from a previously constructed material data-base. This database is populated with experimental data and provides information on their dielectric properties.
PARTICLE SWARM OPTIMIZATION
This algorithm was created by Kennedy and Eberhart in 1995. Thousands of articles have described it, and hundreds have proposed modifications, striving to adapt it to some more complex optimization tasks. A brief description is provided here, focusing on the unified version. Beginning with the traditional PSO:
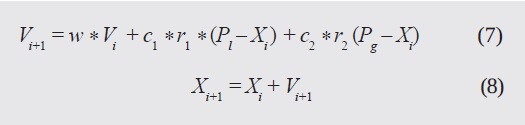
If an N-dimensional space is taken into account, then Xi is a vector that describes the position of each particle, whereas Vi is their velocity. At each iteration, two values are calculated: the particle's best position (Pl) and the swarm's best position (Pg). Finally, there are two positive constants, c1, and c2, that are known as "acceleration coefficients"; w is the inertia weight, and r1, and r2 are uniformly distributed random numbers between 0 and 1. In the unified version, the best local and global information is used to modify the original information, and a local and global velocity, Li, Gi, appear, which use the best position of the neighborhood and of the swarm, Pgi and Pg , respectively. This can be summarized as (Parsopoulos & Vrahatis, 2007):
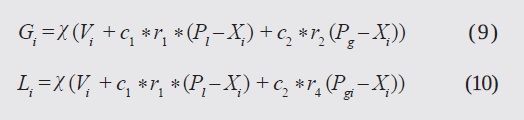
These directions are unified in a single equation:
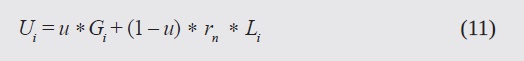
The constriction factor, χ, is introduced to limit the speed of the particles, keeping the swarm from exploding. The unification factor, u, restricts the local and global components, thus enriching the search capabilities of the algorithm. Equation (12) shows the new way of updating positions, which can be seen to be similar to eq. (8), but with unified velocities (Ui).

In order to consider restrictions, a penalty function was included, which modified the objective function by a factor that affected particles outside the feasible area. Thus, the problem transforms into:

where (x) is the objective function, and H(x) is the penalty factor, which varies with the number of iterations, k. H(x) is defined as:
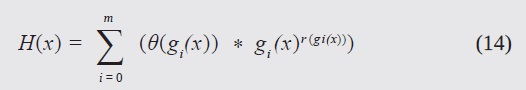
with gi(x) = gi(x) if it is less than zero, and gi(x) = 0 otherwise. The parameters were defined as described in (Parsopoulos & Vrahatis, 2007):

r (gi(x)) is related to the penalty function, i.e. it applies a penalty proportional to the restriction violation. In order for the particles to remain within the search space, it was decided that (Bronwell, 1944):
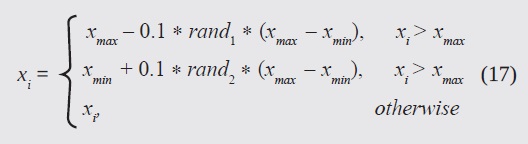
where xmax and xmin define the search space. In a similar fashion, the particles were initialized with a uniform random distribution in this region.
RESULTS AND ANALYSIS
DEFINITION OF THE OPERATING BAND
The absorber was composed of three layers. It was designed to operate in the frequency range of wireless technologies including mobile communications, Bluetooth (2.45 GHz), Wi-Fi (2.45 GHz, 5GHz, 5.4GHz) and ZigBee (0.868 GHz, 0.915 GHz, 2.45 GHz)
UPSO IMPLEMENTATION
The thickness of each layer was defined to be in the range 0.1 mm 2.0 mm, striving to limit the results to a viable solution, since a thick layer is not practical owing to its cost, weight and volume. A heterogeneous mixture of materials in the materials database was defined, as shown in Table 1, where Єr is the dielectric constant and μr is the relative permeability of each material.
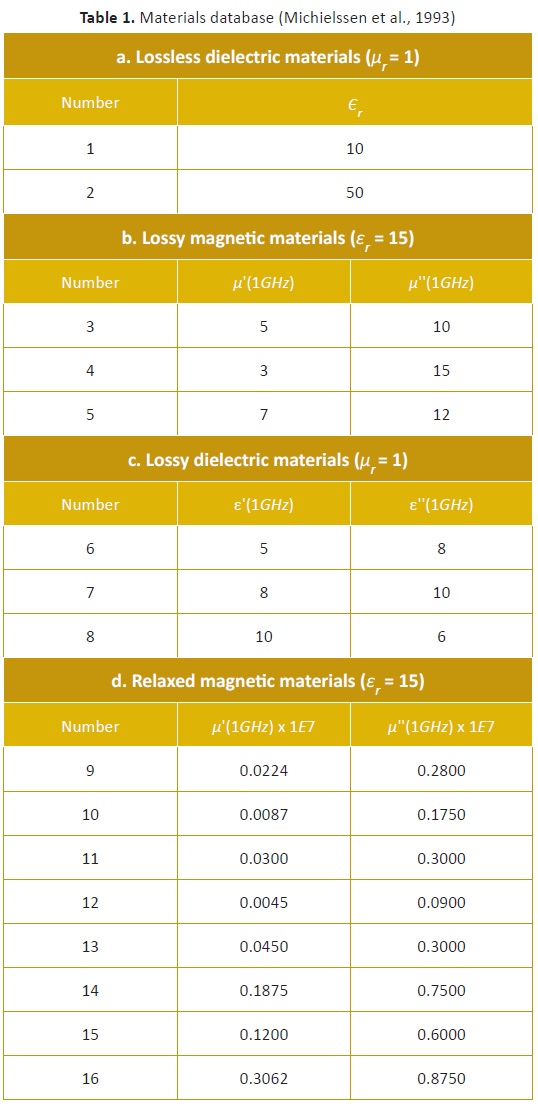
The material for each layer was selected from the available 16. During the simulation, W was varied from 0.9 to 0.4. The constants c1, c2, were equal and assumed to be 1.46. Speed was initialized in a similar way as position (i.e. randomly). The thickness search space was defined between [-0.0021 and 0.0021].
FINAL DESIGN OF THE ABSORBER
It had previously been reported that the algorithm returned three possible designs for the absorber, when solved using PSO. These are summarized in Table 2. When using interval analysis, a solution with a minimum of -21.4605 dB was found, consisting of the same materials, and with thicknesses of [0.5750, 0.6938], [1.8812, 2.0000] and [1.5250, 1.6438] mm, respectively (Salazar & Mora, 2011).
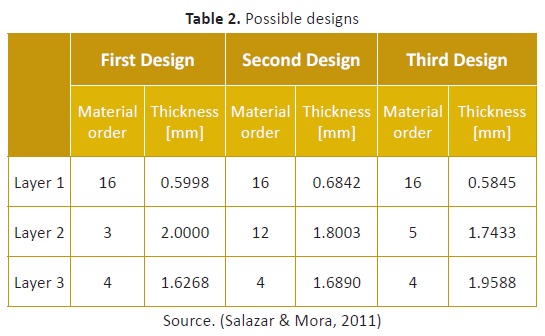
Table 3summarizes some of the results achieved using UPSO, maintaining the same experimental conditions as before, and using a laptop with an Intel Core i7 processor @ 2.20 GHz, 8Gb of RAM and a 64 bit OS.
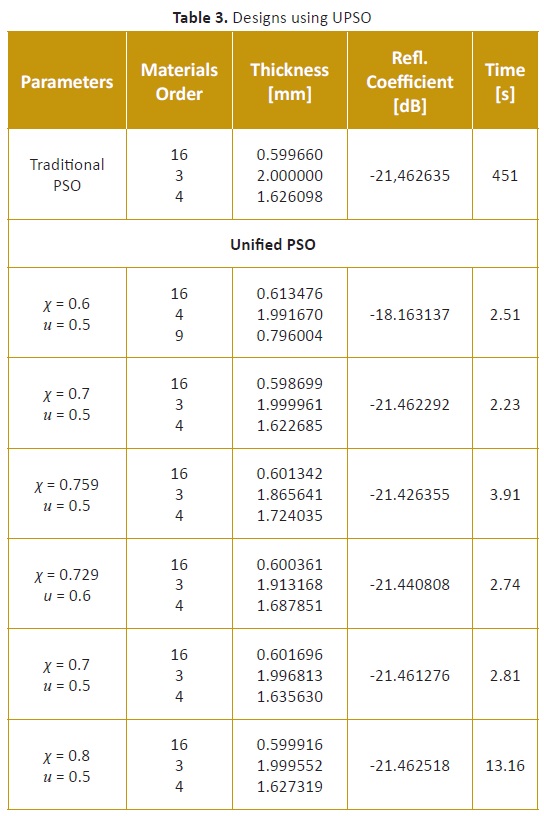
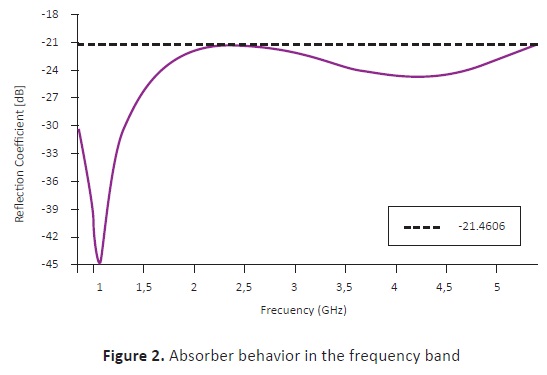
It is observed that the results match quite well with previously reported ones, but were obtained in a shorter time (around 30% less) and with fewer iterations. Regarding the algorithm parameters, the best results were obtained with χ = 0.8 and u = 0.5. Furthermore, good results repeatability was observed for five consecutive iterations, even though for every six runs one different result was returned. The behavior of the best design is summarized in Figure 2. It is important to remark that the horizontal line shown in the figure is the simulation result. This is the optimum, since it has a lower critical point (-21.4606dB), even though all were located in the range [-21.5000 -20.9166]. The average run time was in the order of 5 to 10 minutes, with a success rate of over 99% for five consecutive runs.
CONCLUSIONS
The three-layer EMA showed good performance for the previously defined frequency band (0.85 GHz - 5.4 GHz). A correct selection of the most relevant parameters (e.g. swarm size and boundary criteria) for the unified algorithm increases the likelihood of achieving a correct answer with a minimum number of runs. By comparing both methods, it can be concluded that UPSO is better than the traditional method (PSO), in terms of computation time. Another advantage is that it can easily include more restrictions - for example economic factors -, in order to find, for example, the lowest-cost configuration.
REFERENCES
Bronwell, A. (1944). Transmission-Line Analogies of Plane Electromagnetic-Wave Reflections. Proceedings of the IRE, 32(4), 233-241. doi:10.1109/JRPROC.1944.230657 [ Links ]
Chamaani, S., Mirtaheri, S. A., Teshnehlab, M., & Shoorede li, M. A. (2007). Modified Multi-objective Particle Swarm Optimization for electromagnetic absorber design. In 2007 Asia-Pacific Conference on Applied Electromagnetics (pp. 1-5). IEEE. doi:10.1109/APACE.2007.4603923. [ Links ]
Cui, S., & Weile, D. S. (2005). Application of a Novel Parallel Swarm Optimization to Design Electromagnetic Absorber. Antennas and Propagation Society International Symposium, IEEE, 3616-3624. [ Links ]
Cui, S., Weile, D. S., & Volakis, J. L. (2006). Novel Planar Electromagnetic Absorber Designs Using Genetic Algorithm. IEEE transactions on antennas and propagation, 54(6), 1811-1817. [ Links ]
Liu, H., Zhang, L., Gao, Y., Shen, Y., & Shi, D. (2009). Electromagnetic Wave Absorber Optimal Design Based on Improved Particle Swarm Optimization. EMC 2009, IEICE, 797-800. [ Links ]
M.J., A., & N.I., D. (2010). Design of Multilayer Microwave Broadband Absorbers Using Central Force Optimization. Progress in Electromagnetics Research B, 26, 101-113. [ Links ]
Michielssen, E., Sajer, J.-M., Ranjithan, S., & Mittra, R. (1993). Design of lightweight, broad-band microwave absorbers using genetic algorithms. IEEE Transactions on Microwave Theory and Techniques, 41(6), 1024-1031. doi:10.1109/22.238519 [ Links ]
Parsopoulos, K. E., & Vrahatis, M. N. (2007). Parameter selection and adaptation in Unified Particle Swarm Optimization. Mathematical and Computer Modelling, 46(1-2), 198-213. doi:10.1016/j.mcm.2006.12.019 [ Links ]
Salazar, E., & Mora, J. (2011). Diseño de Absorbedores Electromagnéticos Óptimos Utilizando Optimización por Enjambre de Partículas y Análisis de Intervalos ( B.Sc. Thesis). Universidad Industrial de Santander. [ Links ]













