Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.43 Bogotá July/Dec. 2015
https://doi.org/10.16924/riua.v0i43.861
Expresiones analíticas del coeficiente de pérdidas de energía en dispositivos de reducción del diámetro bajo régimen forzado
Analytical Expressions of the Coefficient of Energy Losses in Diameter Reduction Devices on Forced Regime
José J. Villegas-León (1), Alvaro López-Lambraño (2), José G. Morales-Nava (3), Máximo Pliego-Díaz (4), Carlos Fuentes (5), Alvaro López-Ramos (6)
(1) M.Sc en Ingeniería, Profesor-Asistente, Estudiante de Doctorado, Facultad de Ingeniería, Universidad Autónoma de Baja California (UABC). Baja California, México. juan.villegas@uabc.edu.mx
(2) Ph.D en Ingeniería, Profesor-Investigador, Coordinador del Laboratorio de Hidráulica de la Facultad de Ingeniería, Aquitectura y Diseño, Universidad Autónoma de Baja California (UABC). Baja California, México. Profesor-Investigador, Facultad de Ingeniería, Universidad Autónoma de Baja California (UABC). Baja California, México. Director General, Hidrus S.A de C.V. Querétaro, México. altoti@gmail.com, alopezl@uabc.edu.mx, alopezl@hidrusmx.com.
(3) M.Sc en Ingeniería, Profesor-Investigador, Facultad de Ingeniería, Arquitectura y Diseño, Universidad Autónoma de Baja California (UABC).Baja California, México. jgmnava@uabc.edu.mx
(4) Ph.D en Ingeniería, Profesor-Investigador, Instituto Tecnológico de Querétaro. Ciencias Básicas. Querétaro, México. maxehekatl@yahoo.com.mx
(5) Ph.D en Mecánica de los Fluidos, Profesor-Investigador, Instituto Mexicano de Tecnología del Agua. Morelos, México. cbfuentesr@gmail.com
(6) M.Sc, en Hidrociencias, Profesor-Investigador, Escuela de Ingenierías y Arquitectura, Facultad de Ingeniería Civil, Universidad Pontificia Bolivariana-Seccional Montería. Córdoba, Colombia. alopezramos@hotmail.com
Recibido 13 de agosto de 2015. Modificado 15 de noviembre de 2015. Aprobado 25 de noviembre de 2015.
DOI:http://dx.doi.org/10.16924/riua.v0i43.861
Palabras clave
Coeficiente de pérdidas, dinámica de fluidos, modelación hidráulica, pérdidas hidráulicas.
Resumen
En este artículo se obtienen expresiones analíticas del coeficiente de pérdidas de energía para dispositivos de reducción brusca y reducción gradual del diámetro, que operan en conductos bajo régimen forzado. Se observó que los métodos tradicionales para evaluar las pérdidas por dispositivos requieren el empleo de fórmulas, tablas y gráficos al estimar el coeficiente de pérdida K. Se obtuvieron curvas de valores promedio para K y se ajustaron con métodos de regresiones lineales múltiples hasta obtener una ecuación representativa para cada caso estudiado. Se concluyó que las ecuaciones pueden ser utilizadas confiablemente para determinar el coeficiente de pérdida K, sin necesidad de manipular tablas y gráficos.
Key words
Dynamics of Fluids, Hydraulic Losses, Hydraulic Modeling, Losses Coefficient.
Abstract
Analytical expressions of the energy loss coefficient for abrupt and gradual diameter reduction devices, operating in ducts on forced regime are obtained. For this approach, a state of the art was carried out where it was identified that the traditionally utilized methods (that assess the loss of the devices) needed formulas, tables and/or graphs when estimating the K coefficient. These results were used as data in multiple linear regression methods until a representative equation for each case study was obtained. These equations constitue a reliable tool to determine the loss of the K coefficient without having to manipulate tables and graphs.
Introducción
La importancia de estimar las pérdidas de energía en dispositivos de reducción del diámetro está dada por su utilización en sistemas a presión o en régimen forzado, tales como: líneas de conducción en plantas industriales (Anaya-Durand, Cauich-Segovia, Funabazama-Bárcenas & Gracia-Medrano-Bravo, 2014), redes internas de distribución en centrales geotérmicas (Maria, 2000), conductos de centrales hidroeléctricas (Elbatran, Yaakob, Ahmeda & Shabara, 2015), redes de distribución de agua a poblaciones (Yildirim & Singh, 2010), sistemas de riego (Sesma, Molina-Martínez, Cavas-Martínez & Fernández-Pacheco, 2015), entre otros. La magnitud de las pérdidas depende sustancialmente de resultados experimentales del coeficiente de pérdidas K, que en la literatura son muy discrepantes entre lo especificado por una investigación u otra (Bullen, Cheesema, Hussain & Ruffellt, 1987; Fester, Mbiya & Slatter, 2008).
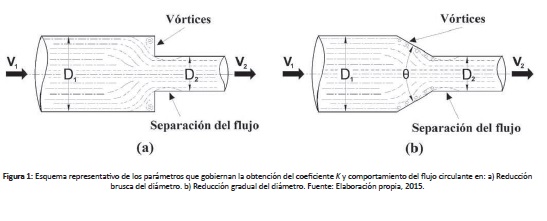
Las pérdidas de energía en los dispositivos de reducción del diámetro ocurren cuando el fluido circula por un conducto de diámetro constante y la sección transversal decrece de forma repentina o gradual. En la figura 1(a) se expone el caso de una reducción brusca, condición que provoca un aumento repentino de la velocidad de circulación, así como también genera turbulencia antes de la reducción. Al iniciar el conducto de área menor se presenta una vena contracta y el flujo alcanza la mayor velocidad. Este fenómeno también ocasiona vórtices aguas abajo del dispositivo, cuando el flujo se estabiliza inician las pérdidas por fricción en el conducto (King & Brater, 1981; Mott, 2006). En la figura 1(b) se ilustra el caso de una reducción gradual, en dicha condición se presenta una transición suave de un diámetro mayor hacia uno menor; el fluido es encausado suavemente hacia un área menor y permite que la velocidad de este incremente a medida que decrece el área transversal (Franzini & Finnemore, 1999; Mott, 2006).
La constante investigación sobre las pérdidas de energía que ocurren en estos dispositivos valida su importancia. Binding, Phillips & Phillips (2006) realizaron un estudio numérico para estimar la pérdida de energía a través de contracciones, expansiones y combinaciones de éstas, utilizando un fluido Oldroyd-B (densidad del fluido más disolvente de 1400 kg/m3, viscosidad total de 10 Pa·s). Ellos tuvieron interés particular en el efecto de la relación del disolvente al parámetro de viscosidad total sobre el perfil del gradiente de presión y sobre las longitudes de desarrollo de entrada y salida; se presentan resultados para ciertos aspectos relacionados con la cinemática del flujo, con el fin de ilustrar la relación entre el campo de presión y el campo de flujo resultante. En Fester et al. (2008) se investigó con fluidos no newtonianos las pérdidas de energía en contracciones súbitas, utilizando relaciones de diámetros de 0,22, 0,50 y 0,85, y números de Reynolds de 0,01 a 100.000, bajo la finalidad de corroborar y ampliar los datos existentes; se presentan un conjunto de resultados experimentales y un modelo numérico validado.
De igual forma, Rend, Sparrow, Bettenhausen & Abraham (2013) hicieron un estudio numérico para determinar la pérdida de energía que se genera en una ampliación gradual utilizada en un sistema de tuberías; se dedujo que la caída de presión incrementa monotónicamente al aumentar el ángulo de dilatación y que, en general, la caída de presión para un ángulo de dilatación dado decrece con el aumento del número de Reynolds y tiende a estabilizarse conforme éste más aumenta. Bae & Kim (2014) investigaron numéricamente con el software Fluent 2.0 de Dinámica Computacional de Fluidos sobre las pérdidas que se producen en una expansión súbita-axisimétrica con chaflán, cuando circula por ésta flujo turbulento; se proponen nuevas correlaciones del coeficiente de pérdidas para las condiciones de número de Reynolds de 30000, ángulo de expansión del chaflán hasta 45º y relaciones de área mayor-área menor del chaflán de 2 a 6.
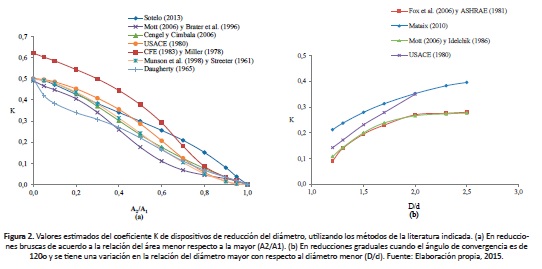
Aunque existen investigaciones valiosas en la literatura, no se ha establecido un valor estándar del coeficiente K para utilizar en dispositivos de reducción brusca o gradual del diámetro. Al emplear un método u otro se obtienen valores distintos del coeficiente (Figura 2). Además, su determinación se rige mediante la utilización de gráficos y tablas.
Ante esta necesidad, en el presente trabajo se obtienen expresiones analíticas que permiten estimar un valor promedio del coeficiente K para los dispositivos en estudio, partiendo de metodologías ampliamente utilizadas. Se obtuvieron curvas de valores promedios para K en cada caso estudiado utilizando modelos de regresiones lineales múltiples, que permiten estimar el coeficiente de pérdida K sin necesidad de manipular tablas y gráficos.
Estimación de pérdidas de energía
De acuerdo a la literatura especializada en el tema como Bariviera, Frizzone & Rettore (2013); Sabersky, Acosta & Hauptmann (1999); Sotelo (2013); Streeter, Wylie & Bedford (2000); USACE (1980); USBR (1985); Yildirim & Singh (2010); entre otros, el estudio de las pérdidas de energía en la reducción del diámetro se clasifica en: reducción brusca y reducción gradual. Ellos también exponen que las pérdidas de energía locales se determinan mediante la siguiente expresión:

Donde hL es la pérdida de carga (m); V es la velocidad media de circulación en el conducto de diámetro reducido (m/s); g es la aceleración de la gravedad (m/s2); K es un coeficiente de pérdidas del dispositivo (adimensional), que se obtiene mediante tablas o gráficos provenientes de resultados experimentales y que a menudo se conjugan con ecuaciones empíricas. Estas informaciones se encuentran en libros, manuales o documentos referentes al tema y su valor es dependiente de parámetros geométricos y físicos del dispositivo y en ocasiones del número de Reynolds (Bae & Kim, 2014).
Sobre la estimación del coeficiente K para la reducción brusca del diámetro, en la literatura se tiene lo siguiente: en Sotelo (2013) y USACE (1980) se establece que el coeficiente K se estima mediante un gráfico con resultados de Weisbach, el cual se rige por la relación del diámetro menor con respecto al diámetro mayor (d/D). Acorde a CFE (1983) y Miller (1978), se sugiere que el coeficiente de pérdidas de este dispositivo se estime a través de un gráfico, donde está supeditado por la relación del área menor con respecto al área mayor (A2/A1). Según Cengel & Cimbala (2006) el coeficiente K para una reducción brusca se determina mediante un gráfico, en el cual se rige por la relación del diámetro menor con respecto al diámetro mayor (d/D). En Brater, King, Lindell & Wei (1996) y Mott (2006) se coincide en que el valor del factor K sea estimado de valores tabulados, donde es definido en función de la velocidad del conducto reducido (V2) y de la relación del diámetro menor con respecto al mayor (d/D). Acorde con Munson, Young & Okiishi (1998) y Streeter (1961), el coeficiente de pérdidas se obtiene con el uso de un gráfico, donde está gobernado por la relación del área menor con respecto a la mayor (A2/A1). Por último, en Daugherty & Me (1965) se expone que el coeficiente de pérdidas se determina con el uso de valores tabulados, donde se encuentra en función de la relación del diámetro menor con respecto al diámetro del conducto mayor (d/D).
Si se produce una reducción gradual del diámetro, de acuerdo con Mataix (2010), el coeficiente K de este dispositivo se determina con la utilización de un gráfico, donde está en función del ángulo de reducción (θ) y de la relación del diámetro mayor con respecto al diámetro menor (D/d). En Fox, Pritchard & Mcdonald (2006) y en ASHRAE (1981) se expone que el coeficiente de esta reducción se obtiene de valores tabulados, donde se encuentra en función del ángulo de reducción (θ) y de la relación del área menor con respecto a la mayor (A2/A1). Basándose en Mott (2006) y Idelchik (1986), dos gráficos abarcan el caso para estimar el coeficiente de pérdidas, donde depende del ángulo de reducción (θ) y de la relación del diámetro mayor con respecto al diámetro menor (D/d). Por último, en USACE (1980) se sugiere el empleo de un gráfico con resultados de Levin para obtener el valor del coeficiente K, conociendo el valor de la relación del diámetro mayor con respecto al menor (D/d) y del ángulo de reducción (θ).
Estimación del coeficiente K
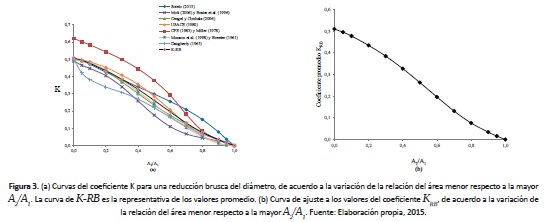
Para la estimación del coeficiente de pérdidas en la reducción brusca, se seleccionaron los métodos que se establecen en Sotelo (2013); Mott (2006); Cengel y Cimbala (2006); USACE (1980); CFE (1983); Munson et al. (1998); Streeter (1961); Brater et al. (1996); Daugherty (1965), en los cuales se utilizan tablas y gráficos para obtener el coeficiente, en función de la relación del área menor con respecto a la mayor (A2/A1). Mediante cada método se obtuvieron valores del coeficiente K para una relación de áreas A2/A1 de 0 a 1, luego se estimaron valores promedio que se denotan por KRB. En la figura 3(a) se exhiben estos resultados, en los cuales se observa la variabilidad del coeficiente K entre un método y otro para una misma relación de áreas. Al utilizar los valores de KRB, se trabajó con regresión lineal múltiple, donde se seleccionó la curva de ajuste que se presenta en la figura 3(b) y su ecuación es la propuesta para estimar el coeficiente de este dispositivo, la cual se escribe de la forma siguiente:
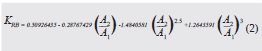
Donde KRG es el coeficiente de pérdidas de una reducción gradual del diámetro; D/d es el valor de la relación área menor con respecto a la mayor. Esta ecuación es válida para 0 = A2/A1 <1.
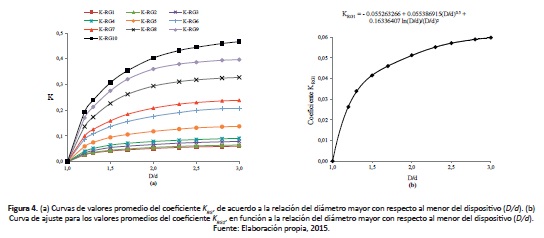
Por otra parte, para estimar el coeficiente de pérdidas en dispositivos de reducción gradual, se analizaron los métodos expuestos en Mott (2006); USACE (1980); Fox et al. (2006); Mataix (2010); ASHRAE (1981); Idelchik (1986); con los que se procedió de forma similar a la reducción brusca. Para obtener la expresión que estima el valor de KRG se realizaron 10 clasificaciones. En primer lugar, se determinaron valores promedio denotados como KRG1, donde la relación del diámetro mayor con respecto al menor (D/d) toma valores de 1 a 3 y se presenta un ángulo de reducción (θ) de 10o. De la misma manera, se determinaron valores promedio del coeficiente de pérdidas cuando se tiene un ángulo θ de 20, 30, 40, 60, 80, 90, 120, 150 y 1800, los cuales se denotan como KRG2, KRG3, KRG4, KRG5, KRG6, KRG7, KRG8, KRG9 y KRG10, respectivamente, como se ilustra en la figura 4(a); además se emplearon modelos de regresiones lineales múltiples para obtener una curva de ajuste y su respectiva ecuación para las clasificaciones de KRG establecidas anteriormente; en la figura 4(b) se muestra el modelo obtenido para KRG1 y su respectiva ecuación. La expresión general de KRG para cualquier clasificación está dada de la siguiente manera:
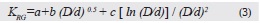


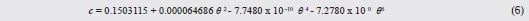
donde: KRG es el coeficiente de pérdidas de una reducción gradual del diámetro; θ es el ángulo de reducción del dispositivo (en grados); D/d es la relación del diámetro mayor con respecto al menor del dispositivo; a, b, c son coeficientes que dependen del ángulo de la reducción (θ). Debido a que los coeficientes a, b y c varían de acuerdo a la magnitud de θ, se obtuvo una curva de ajuste para los valores de cada uno de ellos. La ecuación de la curva ajustada a los valores del coeficiente a, se escribe en la ecuación (4); se obtuvieron de forma similar las ecuaciones (5) y (6) para estimar el coeficiente b y c, respectivamente.
donde: a, b y c son los coeficientes de la ecuación (4); θ es el ángulo de la reducción (grados).
Al sustituir las ecuaciones de cada coeficiente en la ecuación (3), esta queda de la siguiente manera:

donde: KRG es el coeficiente de pérdidas de una reducción gradual del diámetro; ? es el ángulo de reducción del dispositivo (en grados); D/d es la relación del diámetro mayor con respecto al menor. La ecuación anterior es válida para 1 < D/d ≤ 3 y 10 ≤ θ ≤ 180º.
Casos de aplicación para la evaluación y comparación de pérdidas de energía
Ampliación brusca del diámetro
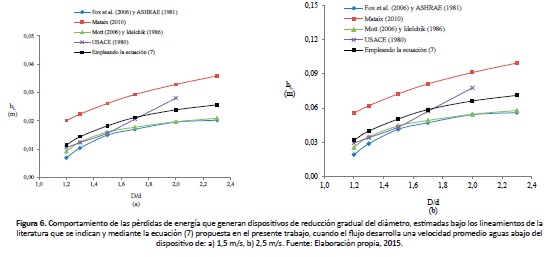
Caso 1: Se considera que un flujo circulante adquiere una velocidad promedio de 1,5 m/s aguas abajo de dispositivos de reducción brusca, que en conjunto presentan relaciones de áreas (A2/A1) de 0,1 a 0,9 en incrementos de 0,1. Al emplear los métodos analizados para este accesorio y la ecuación propuesta en esta investigación, se determinan las pérdidas de energía mediante la aplicación de la ecuación (1) y las cantidades resultantes se exponen en la figura 5(a) .
Caso 2: Si se asumen las mismas condiciones que en el caso anterior, excepto que la velocidad media de circulación ahora se presenta en 2,5 m/s, se determinan las pérdidas de energía en el dispositivo y los resultados se ilustran en la figura 5(b) .
En la figura anterior se puede apreciar el aumento de la pérdida de energía al decrecer la relación de áreas (A2/A1), debido a que la obstrucción del flujo aumenta al decrecer esta relación. También se puede constatar la variabilidad de las pérdidas de energía que se obtienen utilizando un método u otro, para una misma relación de áreas y velocidad de circulación del flujo. Sin embargo, se ilustra claramente que las pérdidas de energía obtenidas mediante la ecuación (2), tienen una tendencia a la media. Por otro lado, podemos distinguir los métodos que estiman los valores mayores y menores de pérdidas de energía. Las mayores pérdidas se obtienen utilizando el método de CFE (1983) y Miller (1978) cuando 0,1 ≤ A2/A1 ≤ 0,6. Si 0,7 ≤ A2/A1 ≤ 0,9, entonces las mayores pérdidas resultan con el método de Sotelo (2013). Finalmente, las menores pérdidas de energía se obtienen utilizando el método de Daugherty y Me (1965) cuando 0,1 ≤ A2/A1 ≤ 0,3; si 0,4 ≤ A2/A1 ≤ 0,8, entonces las menores pérdidas se estiman con el método de Mott (2006) y Brater et al. (1996).
Ampliación gradual del diámetro
Caso 1: Flujo con una velocidad promedio de 1,5 m/s inmediatamente aguas abajo de dispositivos de reducción gradual, que presentan un ángulo de reducción (θ) de 90º y en conjunto, relaciones de diámetro (D/d) de 1,2, 1,3, 1,5, 1,7, 2,0 y 2,3. Se determinan las pérdidas de energía en los dispositivos y las magnitudes se ilustran en la figura 6(a).
Caso 2: Bajo las mismas condiciones del caso anterior, excepto que el flujo aumenta su velocidad media a 2,5 m/s, se determinan las pérdidas de energía en los dispositivos de reducción gradual y los resultados se exponen en la figura 6(b).
En la figura 6, podemos visualizar la discrepancia entre las pérdidas de energía que se obtienen con distintos métodos sugeridos en la literatura, mientras que con la ecuación (7), se estiman valores intermedios a los rangos entre valores máximos y mínimos. También se observa que las mayores pérdidas de energía se obtienen utilizando el método de Mataix (2010), para cualquier valor de D/d. Por último, se ilustra que las menores pérdidas de energía se estiman empleando el método de Fox et al. (2006) y ASHRAE (1981) para cualquier valor de D/d, excepto cuando D/d = 2.
Conclusiones
Los métodos utilizados tradicionalmente para la estimación del coeficiente K en los dispositivos estudiados proporcionan entre sí valores diferentes del coeficiente y además requieren la utilización de tablas y gráficos. A partir de los valores de K reportados en dichas metodologías, se obtuvieron expresiones analíticas que permiten estimar los valores promedio del coeficiente K para reducciones bruscas y graduales. Para la condición de reducción brusca únicamente se requiere el valor de la relación del área menor con respecto al área mayor (A2/A1) y, para la condición de reducción gradual se requiere el valor del ángulo de la reducción (θ) y la relación del diámetro mayor con respecto al menor (D/d). En los casos de aplicación para evaluar y comparar las pérdidas de energía se demostró la facilidad para obtener el coeficiente K utilizando las expresiones propuestas. Con esto se evidencia la utilidad y practicidad de dichas ecuaciones para usarlas en el diseño y la comprobación del comportamiento hidráulico de los conductos forzados, evitando la manipulación de tablas y gráficos como comúnmente se hace. Por lo tanto, se exhorta a ser programadas en algoritmos de cómputo que involucren el análisis y la modelación de las pérdidas de energía en distintos sistemas hidráulicos, tales como: obras de toma, líneas de aducción y conducción, redes de distribución de agua potable, sistemas de irrigación, conductos o redes en plantas geotérmicas, entre otras, para facilitar el trabajo del usuario en el proceso de entrada de datos al sistema. Finalmente, la presente investigación se podría complementar obteniendo expresiones analíticas que estimen el valor del coeficiente de pérdidas K, tomando en consideración el número de Reynolds, además de los parámetros geométricos.
Referencias
American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). (1981). Handbook-Fundamentals. Georgia, USA: American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc. [ Links ]
Anaya-Durand, A. I., Cauich-Segovia, G. I., Funabazama-Bárcenas, O. & Gracia-Medrano-Bravo, V.A. (2014). Evaluación de ecuaciones de factor de fricción explícito para tuberías. Revista Mexicana Ingeniería Química, 25(2), 128-134. doi: 10.1016/S0187-893X(14)70535-X. [ Links ]
Bae, Y. & Kim, Y. (2014). Prediction of local loss coefficient for turbulent flow in axisymmetric sudden expansions with a chamfer: Effect of Reynolds number. Journal Annals of Nuclear Energy, 73, 33-38. doi:10.1016/j.anucene.2014.06.032. [ Links ]
Bariviera, D., Frizzone, J. A. & Rettore, N. O. (2013). Dimensional analysis approach to estimate local head losses in microirrigation connectors. Journal Irrigation Science, 32(3), 169-179. doi: 10.1007/s00271-013-0424-y. [ Links ]
Binding, D. M., Phillips, P. M. & Phillips T. N. (2006). Contraction/expansion flows: The pressure drop and related issues. Journal of Non-Newtonian Fluid Mechanics, 137, 31-38. doi:10.1016/j.jnnfm.2006.03.006. [ Links ]
Brater, E. F., King, H. W., Lindell, J. E. & Wei, C. Y. (1996). Handbook of Hydraulics. USA: Mc Graw-Hill. [ Links ]
Bullen, P. R., Cheesema, D. J., Hussain, L. A. & Ruffellt A.E. (1987). The determination of pipe contraction pressure loss coefficients for incompressible turbulent flow. International Journal of Heat and Fluid Flow, 8(2), 111-118. doi:10.1016/0142-727X(87)90008-7. [ Links ]
Cengel, Y. A. & Cimbala, J. M. (2006). Mecánica de fluidos, Fundamentos y Aplicaciones. México D.F.: Editorial Mc Graw-Hill, Interamericana. [ Links ]
Comisión Federal de Electricidad (CFE). (1983). Manual de Obras Civiles: Tomo 2.3 Conducciones a Presión. México D.F.: Instituto de Investigaciones Eléctricas. [ Links ]
Daugherty, R. L. & Me, A. B. (1965). Fluid Mechanics, With Engineering Applications. USA: Mc Graw-Hill. [ Links ]
Elbatran, A. H., Yaakob, O. B., Ahmeda Y. M. & Shabara, H. M. (2015). Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. J. Renewable and Sustainable Energy Reviews, 43, 40-50. doi:10.1016/j.rser.2014.11.045. [ Links ]
Fester, V., Mbiya, B. & Slatter, P. (2008). Energy losses of non-Newtonian fluids in sudden pipe contractions. Chemical Engineering Journal, 145, 57-63. doi:10.1016/j.cej.2008.03.003. [ Links ]
Fox, R. W., Pritchard, P. J. & Mcdonald, A. T. (2006). Introduction To Fluid Mechanics. USA: John Wiley & Son Inc. [ Links ]
Franzini, J. B. & Finnemore, E. J. (1999). Mecánica de fluidos, con aplicaciones en ingeniería. España: Editorial Mc Graw-Hill, Inc. [ Links ]
Idelchik, I. E. (1986). Handbook of Hydraulic Resistance. New York, USA: Harper and Row. [ Links ]
King, W. H. & Brater, E. F. (1981). Manual de Hidráulica. México D.F: UTEHA. [ Links ]
Maria, F. D. (2000). Design and off design pipe network geothermal power plant analysis with power pipe simulator. J. Energy Conversion & Management, 41(12), 1223-1235. doi:10.1016/S0196-8904(99)00177-6. [ Links ]
Mataix, C. (2010). Mecánica de Fluidos y Máquinas Hidráulicas. México: Editorial Alfaomega. [ Links ]
Miller, D. S. (1978). Internal flow systems. UK: BHRA (information services). [ Links ]
Mott, R. L. (2006). Mecánica de Fluidos. México: Pearson Educación. [ Links ]
Munson, B. R., Young, D. F. & Okiishi, T. H. (1998). Fundamentals of Fluid Mechanics. New York, USA: John Wiley & Son. [ Links ]
Rend, R. R., Sparrow, E. M., Bettenhausen, D. W. & Abraham, J.P. (2013). Parasitic pressure losses in diffusers and in their downstream piping systems for fluid flow and heat transfer. International Journal of Heat and Mass Transfer, 61, 56-61. doi:10.1016/j.ijheatmasstransfer.2013.02.002. [ Links ]
Sabersky, R. H., Acosta, A. J. & Hauptmann, E. G. (1999). Fluid Flow, a first course in fluid mechanics. USA: Prentice-Hall, Inc. [ Links ]
Sesma, J., Molina-Martínez, J. M., Cavas-Martínez, F. & Fernández-Pacheco, D. G. (2015). A mobile application to calculate optimum drip irrigation laterals. J. Agricultural Water Management, 151, 13-18. doi:10.1016/j.agwat.2014.09.026. [ Links ]
Sotelo, A. G. (2013). Hidráulica General. México D.F.: LIMUSA. [ Links ]
Streeter, V. L. (1961). Handbook of Fluid Dynamics. New York, USA: McGraw-Hill. [ Links ]
Streeter, V. L., Wylie, E. B. & Bedford, K. B. (2000). Mecánica de fluidos. Bogotá, Colombia: Mc Graw-Hill Internacional SA. [ Links ]
United States Army Corps of Engineers (USACE). (1980). Engineering and Design, Hydraulic Design of Reservoir Outlet. Recuperado de http://publications.usace.army.mil/publications/eng-manuals/EM_111021602_sec/EM_1110-2-1602.pdf. [ Links ]
United States Bureau of Reclamation (USBR). (1985). Diseño de Presas Pequeñas. United States Department of the Interior, Bureau of Reclamation. México D. F.: Compañía Editorial Continental, SA de CV. [ Links ]
Yıldırım, G. & Singh. V. P. (2010). A MathCAD procedure for commercial pipeline hydraulic design considering local energy losses. Advances in Engineering Software, 41, 489-496. DOI: 10.1016/j.advengsoft.2009.10.007. [ Links ]