Yuji Ijiri & Robert Kaplan**

* La versión original en inglés de este artículo “Probabilistic depreciation and its implications for group depreciation” fue publicada en The Accounting Review, vol. 44, No. 4. octubre 1969, pp. 743-756, y está disponible en línea en http://aaahq.org/pubs.cfm. Los derechos sobre la versión original en inglés, pertenecen a los autores y a la American Accounting Association (AAA), que amablemente concedieron la autorización para publicar esta versión en español. La AAA no ha revisado esta traducción razón por la cual no se responsabiliza por la calidad de la misma.

** La traducción fue elaborada por Nohora García, profesora de la Universidad Nacional de Colombia, Sede Bogotá, quien agradece la colaboración recibida de Bill Dickinson y Fernedy Martínez. La traductora desea agradecer también a Dreidre Harris de la AAA, por su amable ayuda en el proceso de autorización para publicar esta versión en español.

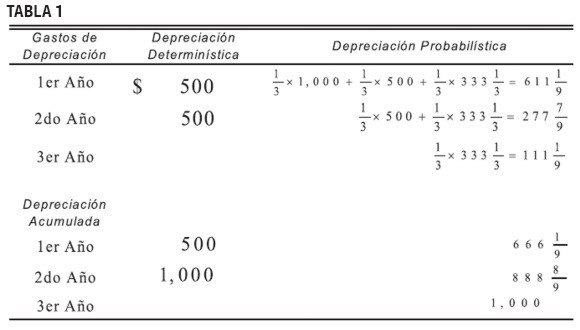
La depreciación es el método de asignación del costo depreciable (costo de adquisición menos valor de salvamento) de un activo a través de su vida de servicio. Un activo alcanza el fin de su vida de servicio debido al deterioro físico y daño o debido a la obsolescencia técnica. El gasto de depreciación asignado al final de un periodo debe reflejar la parte del servicio potencial total que ha expirado durante el periodo[1]. Si se espera que el servicio de un activo sea distribuido uniformemente a través de su vida sin deteriorarse, se utiliza la depreciación de línea recta; este método asigna una cantidad igual cada año durante la vida del activo. Si se espera que el servicio del activo se deteriore durante su vida, los métodos de depreciación acelerada se utilizan para asignar mayores gastos a los primeros años de la vida del activo.

Claramente, la vida de servicio de un activo es un factor crucial para computar la depreciación. Sin embargo, rara vez ésta se conoce anticipadamente con certeza. La depreciación generalmente se estima con base en la vida promedio de activos de la misma clase o activos similares que ha sido utilizados en el pasado. En los métodos de depreciación convencionales, el gasto de depreciación para cada periodo está basado únicamente en el promedio estimado de la vida de servicio. En este documento, nosotros mostramos que incluso si los métodos de depreciación acelerada son utilizados o no, los métodos de depreciación convencional generalmente conducen a una subdepreciación en los primeros periodos de la vida de un activo, comparada con un método más exacto en el que la depreciación es computada para cada posible vida de servicio del activo y luego calculado el promedio. Si se calcula el promedio antes o después de que los gastos de depreciación sean obtenidos, se puede crear una diferencia significativa en los patrones de depreciación sobre la vida del activo, como lo veremos en este documento. Por conveniencia, llamaremos al método convencional depreciación Determinística, y al método propuesto depreciación Probabilística.

Para una sencilla ilustración de nuestro punto, vamos a considerar tres máquinas de un tipo idéntico cuyas vidas de servicio son uno, dos y tres años, respectivamente, que proporcionan un servicio uniforme durante sus vidas. Si el costo depreciable de cada máquina es $1.000, depreciaríamos en el primer año $1.000 para la máquina con un año de vida, $500 para la máquina con dos años de vida y $333 1/3 para la máquina con tres años de vida, para un total de 1.833 1/3. Los gastos de depreciación para el segundo y el tercer periodo son obtenidos similarmente, siendo $833 1/3 y $333 1/3, respectivamente.

Este cálculo está, por supuesto, basado en el supuesto de que la vida de servicio de las máquinas es conocida anticipadamente con certeza. Sin embargo, supongamos que hace tres años compramos tres máquinas y observamos que sus vidas eran uno, dos y tres años, respectivamente. Supongamos además que ahora compramos una nueva máquina del mismo tipo. A menos que exista una razón para creer que el patrón de vida de servicio de la nueva máquina sería diferente del de las viejas máquinas, esperaremos que la nueva máquina tenga una igual probabilidad de servir uno, dos y tres años. Entonces, la vida de servicio promedio de esta nueva máquina sería estimada en dos años, y según el método Determinístico podríamos depreciar $500 en cada uno de los primeros dos años de servicio.

Sin embargo, de acuerdo con el método de depreciación Probabilística, calculamos los gastos de depreciación para el primer año según cada posible vida de servicio. Si la máquina logra durar sólo un año, depreciaríamos $1.000 en el primer año. Si la máquina logra durar dos años de servicio, depreciaríamos $500 en cada uno de los primeros dos años. Si la máquina logra durar tres años de servicio, depreciaríamos $333 1/3 en cada uno de los tres años. Dado que cada evento es igualmente probable que ocurra, el servicio potencial esperado que expirará en el primer año es obtenido tomando el promedio de las tres cifras, es decir: ($1.000 + $500 + $333 1/3)/3 = 611 1/9. La tabla 1 muestra los cálculos para los gastos de depreciación para cada uno de los tres años bajo los métodos Determinístico y Probabilístico.

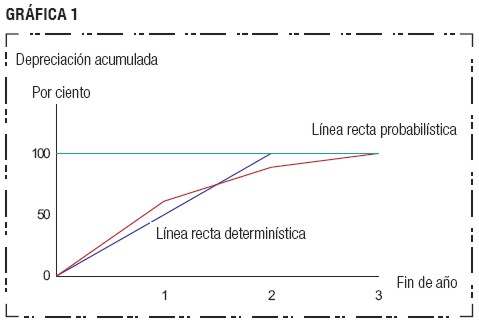
La diferencia en la depreciación acumulada según los dos métodos también se presenta en la gráfica 1. Debido a los altos gastos de depreciación en los primeros periodos, la depreciación acumulada es mayor bajo la depreciación Probabilística que bajo depreciación Determinística. Mientras que el activo es totalmente depreciado al final de la vida promedio estimada bajo la depreciación Determinística, no ocurre lo mismo al final de la más larga vida posible del activo bajo depreciación Probabilística. Por tanto, la depreciación acumulada bajo el método de depreciación Determinística excede la obtenida bajo el método de depreciación Probabilística en algún punto antes del fin de la vida promedio estimada[2].

En el apéndice 1 probamos que para cualquier método de depreciación donde la depreciación del primer año disminuye a una tasa decreciente, la depreciación del primer año es siempre mayor bajo depreciación Probabilística que bajo depreciación Determinística, sea cual sea la distribución de probabilidad de la vida de servicio. Los tres métodos de depreciación más comúnmente utilizados –a saber, el método de línea recta, el método de la suma de los dígitos de los años, el método del doble saldo decreciente– tienen todos esta propiedad. Además, probamos que, para cualquier método de depreciación que satisface la anterior condición y para el que el gasto de depreciación anual no está incrementando durante la vida de servicio, la depreciación acumulada bajo la depreciación Probabilística excede la depreciación Determinística hasta cierto punto en el tiempo. Después de tal punto la última llega a ser mayor que la primera durante la vida de servicio restante. El punto particular en el tiempo en el que los dos métodos se cruzan depende de la distribución de probabilidad de la vida de servicio y del método de depreciación particular adoptado (acelerado o no acelerado).

Es posible obtener un indicador cualitativo de los factores que afectan las diferencias entre los gastos de depreciación bajo los métodos de depreciación Probabilística y depreciación Determinística. Tomaremos como ejemplo el método de línea recta, aunque la conclusión puede ser generalizada al método de la suma de los dígitos de los años y al método del doble saldo decreciente. Por el método de línea recta, el gasto de depreciación en el primer año puede ser expresado como una función de la vida de servicio como se muestra en la gráfica 2.

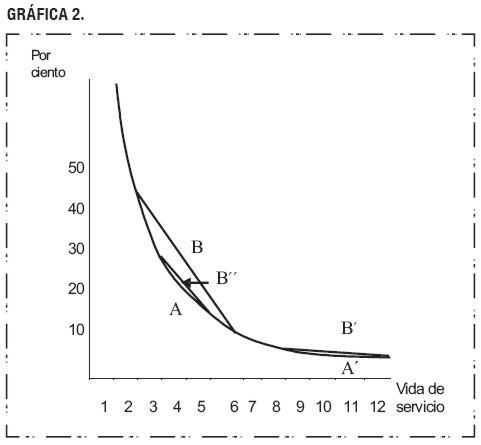
De acuerdo con el método de depreciación Determinística, la vida de servicio promedio se calcula primero (es decir, cuatro años) y luego se obtiene el gasto de depreciación (es decir, el punto A); mientras que de acuerdo con el método de depreciación Probabilística, los gastos de depreciación para cada posible vida de servicio son calculados (es decir, 2-6 años con igual probabilidad) y luego se obtiene el promedio de los gastos (es decir, el punto B). Según la gráfica 2, es evidente que la diferencia en los gastos de depreciación bajo las dos políticas (a saber, B-A en la gráfica 2) depende de dos factores. Uno es la vida de servicio esperada y el otro es el rango de posibilidades de la vida de servicio. Si la vida esperada de servicio llega a ser mayor, la diferencia en los gastos de depreciación llega a ser más pequeña (véase la diferencia entre B´ y A´, B´ – A´). También, si el rango de posibilidades de la vida de servicio llega a ser más pequeño (es decir, la distribución de las posibilidades de vida útil se concentra más alrededor de la vida de servicio esperada), la diferencia en los gastos de depreciación llega a ser más pequeña (véase la diferencia B´ – A comparada con B – A).

Por ejemplo, para una máquina con una vida de servicio de 3, 4, 5, 6 ó 7 años, cada una con una igual probabilidad de ocurrencia, el gasto de depreciación en cada año para los primeros tres años bajo depreciación de línea recta Probabilística es el promedio de 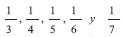ó 21,9%, mientras que la misma bajo depreciación de línea recta Determinística es 20%, puesto que la vida de servicio promedio es cinco años. Esto crea aproximadamente un error del 10%. De otro lado, para una máquina con la misma distribución, pero una vida de servicio esperada mayor, por ejemplo, 8, 9, 10, 11 ó 12 años, cada una con igual probabilidad de ocurrencia, el gasto de depreciación en cada uno de los primeros ocho años de acuerdo con el método de depreciación de línea recta probabilística es 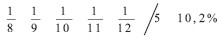comparado con 10% bajo el método de depreciación de línea recta Determinístico, creando sólo un error de 2,0%. Sin embargo, la diferencia es incrementada si aumentamos las posibles vidas de servicio, por ejemplo, cinco años, con igual probabilidad de ocurrencia. Por tanto, el método de depreciación de línea recta Probabilística ahora nos da 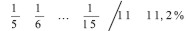para los primeros cinco años, mientras que de acuerdo con el método de depreciación de línea recta Determinístico nos da el mismo 10%, puesto que la vida de servicio esperada no cambia. La tasa de error ahora aumenta a más del 10%.

En general, este comportamiento puede ser explicado al reconocer que dado que la vida de servicio esperada incrementa y el rango de esta vida de servicio esperada disminuye, la función que computa el gasto de depreciación bajo el método de depreciación Probabilística puede ser aproximada por una función lineal de la vida de servicio. Recordemos que la diferencia entre el método de depreciación Probabilístico y el Determinístico se origina debido a la diferencia cuando se computa la esperanza. Si la función cuya esperanza es tomada, pero es lineal, la esperanza de la función iguala la función de los valores esperados y los dos métodos darán resultados similares.

Por consiguiente, puede ser que consideremos la convencional depreciación Determinística una aproximación a la más exacta depreciación Probabilística, cuya aproximación es satisfactoria cuando la vida de servicio esperada es grande y las posibles vidas de servicio se concentran más alrededor de la vida de servicio esperada. Si estas condiciones no se mantienen, debemos hacer una estimación de la distribución de probabilidad de las vidas de servicio, con el fin de utilizar la depreciación Probabilística, de modo que los servicios previstos consumidos en cada periodo puedan ser reflejados más exactamente.

Distribuciones empíricas

En la práctica, puede ser difícil obtener estimaciones de la probabilidad p_i i 1, 2,..., n de la vida de servicio que es igual a i periodos[3]. Sin embargo, una aproximación a la distribución de la vida de servicio puede ser posible asumiendo una forma dada para la distribución de probabilidad, de modo que sólo uno o dos parámetros especifiquen toda la distribución.

Por ejemplo, si se espera que la distribución actual sea simétrica alrededor de la vida de servicio promedio, una aproximación por la distribución normal puede ser satisfactoria (véase la gráfica 3a). Esta aproximación sólo requiere una estimación de la media y la varianza. Alternativamente, si se espera que el número de retiros para cada periodo en un intervalo sea relativamente constante, una distribución rectangular puede ser utilizada para el intervalo (véase gráfica 3b). Ésta también requiere especificar dos valores: el límite superior y el inferior de la distribución. Si se espera que la distribución actual sea sesgada hacia los últimos periodos, una distribución Poisson puede proporcionar una buena aproximación (véase gráfica 3c). Si se espera que la probabilidad de retiro en cualquier periodo sea una constante, independiente de la edad del activo, una distribución geométrica puede ser útil (véase gráfica 3d). La distribución Poisson sólo requiere una estimación de la vida esperada, y la distribución geométrica sólo requiere una estimación de la probabilidad de retiro (constante) en cada periodo para determinar completamente la distribución. La elección de una distribución particular para calcular la depreciación Probabilística debe hacerse sólo después de un estudio cuidadoso de las vidas de servicio de los mismos activos o activos similares utilizados en el pasado.

Para lograr una mejor idea de las diferencias entre la depreciación Probabilística y la Determinística en la práctica, consideramos el caso donde la vida de servicio de un activo tiene una distribución Poisson[4]. Dejemos que DD(i,L) sea el gasto de depreciación para el año i para un activo con una vida de servicio esperada de L años bajo el método de depreciación Determinística, y dejemos que DD(i,L) sea la misma cantidad bajo el método de depreciación Probabilística[5]. Sabemos de la discusión en la sección 1 que DP(1,L) > DD(1,L); por tanto, [DP (1,L) – DD(1,L)] ⁄ DD (1,L) nos da el porcentaje de incremento en el primer año de depreciación si se usa la depreciación Probabilística en lugar de la Determinística. La columna 2 en la tabla 2 nos da el porcentaje para los valores de la vida de servicio esperada que se extiende desde los 2 hasta los 11 años. La columna 3 indica el último año en el que el gasto de depreciación bajo depreciación Probabilística excede éste bajo depreciación Determinística. Puede verse que para aproximarse a la media de la vida de servicio esperada, el método Probabilístico genera un gasto de depreciación más alto que el método Determinístico, acelerando de este modo la depreciación en los primeros años. La depreciación acumulada es mayor bajo el método Probabilístico que bajo el método Determinístico hasta e incluyendo el año dado en la cuarta columna de la tabla 2.

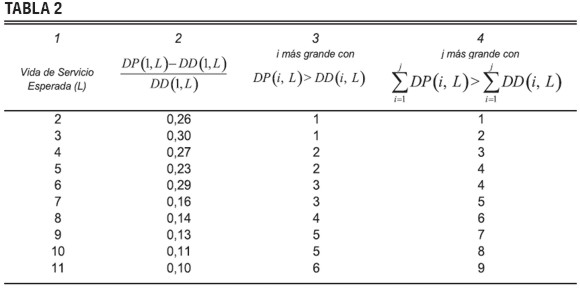
De esta tabla podemos ver que con nuestros supuestos de depreciación de línea recta y la distribución Poisson de las vidas de servicio, el uso del método Determinístico subestima considerablemente la verdadera depreciación en los primeros años de servicio del activo.

Depreciación en grupos

Nuestra discusión ha estado limitada al uso de la depreciación Probabilística para la depreciación de activos individuales. Sin embargo, la depreciación de grupos es una importante área donde esta idea puede ser aplicada inmediatamente, puesto que los datos necesarios para estimar la distribución de probabilidad de las vidas de servicio están generalmente disponibles[5a].

En la depreciación de grupos, todos los ítems con características similares se agrupan juntos en un solo grupo de activos. Las ganancias o pérdidas del retiro de ítems individuales no son reconocidas, pero pueden ser adicionadas o sustraídas a la depreciación acumulada, que es llevada para todos los activos en el grupo. Tales ganancias o pérdidas son reconocidas sólo cuando todos los activos en el grupo son retirados completamente.

Una justificación principal para el uso de un método para el grupo es que incluso ítems idénticos en el momento de la compra (es decir, camiones de una flota, unidades de aire acondicionado para una planta o para un motel) tendrán una vida de servicio actual diferente debido al envejecimiento probabilístico o a un proceso fallado. Luego, más que llevar una cuenta separada para cada uno de estos ítems y depreciar con base en la vida de servicio esperada, considerables ahorros en la teneduría son logrados al agrupar tales ítems en una sola cuenta de activo.

Los gastos de depreciación para la depreciación de un grupo son calculados con base en las curvas de mortalidad de un grupo de activos. Estas curvas dan la proporción de artículos que se esperan sean retirados en un periodo dado. Haciendo la asociación natural entre la proporción retirada en un periodo y la probabilidad de retiro para un solo artículo se obtiene la probabilidad de la vida de servicio, P_i, la probabilidad de que un retiro ocurra en el periodo i. Sin embargo, quizás debido a la carencia de un modelo que considere explícitamente la depreciación para activos con vidas de servicio probabilística, la información probabilística detallada disponible de tales curvas de mortalidad no ha sido explotada en la depreciación convencional de grupos[6]. Además, la vida de servicio esperada es calculada ponderando el periodo de falla con la proporción esperada de falla en tal periodo y usando esta cifra como una base para la depreciación del grupo.

Por ejemplo, consideremos las tres máquinas mencionadas en la sección anterior, donde las probabilidades de falla en el primer, segundo y tercer año son iguales a ¹/₃. Según la convencional depreciación de un grupo, la vida de servicio promedio es calculada en dos años y, por tanto, 50% del costo de depreciación de las máquinas que están aún en servicio al comienzo del año es asignada al año. La tabla 3 muestra los gastos de depreciación para los tres años. Según la depreciación Probabilística, los gastos de depreciación son calculados como se muestra en la tabla 4.

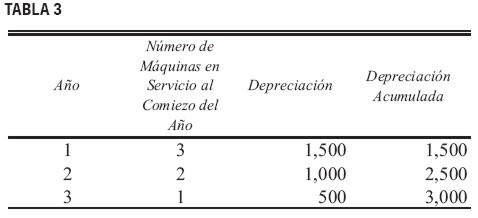
Comparando las gráficas en las tablas 3 y 4, fácilmente puede verse que la depreciación convencional de grupos termina en una subdepreciación para todos los periodos hasta la vida máxima de servicio. (Para el caso de una sola máquina, la depreciación acumulada según el método de depreciación convencional llega a ser mayor que bajo el método Probabilístico en algún punto antes del final de la vida de servicio promedio estimada como se muestra en la gráfica 1, pero esto no ocurre en el caso de la depreciación de grupos). En el apéndice 1 mostramos que si el comportamiento real de las fallas de la máquina sigue el comportamiento esperado, la depreciación acumulada bajo el método convencional es siempre menor que o igual a ésta bajo el método Probabilístico para la depreciación de línea recta.

Con el fin de ilustrar el punto anterior con un ejemplo un poco más complicado, vamos a considerar cien máquinas idénticas con un costo depreciable de $1.000 cada una. La historia reciente de máquinas similares muestra la distribución de las vidas de servicio según se presenta en la tabla 5[7]. Asumiendo que el retiro ocurre sólo al final del año indicado, la vida de servicio promedio es calculada en cinco años. Por tanto, la depreciación de grupos convencional, 20% del costo depreciable de las máquinas que están en servicio durante el año, es asignada al año. Esto también se muestra en la tabla 5.

De acuerdo con el método Probabilístico, los gastos de depreciación son calculados como se muestra en la tabla 6. De nuevo, al comparar la columna de la depreciación acumulada en las tablas 5 y 6 puede verse la depreciación de grupos convencional subvalorada con relación al método Probabilístico.

Conclusiones

En este documento hemos anotado que la depreciación convencional, con base en la vida de servicio esperada, es una aproximación a la depreciación Probabilística, que es teóricamente más exacta. La aproximación es buena sólo cuando la vida de servicio esperada es relativamente larga y las posibles vidas de servicio están concentradas alrededor de la vida de servicio esperada. Cuando esto no es verdad, debe hacerse un esfuerzo para estimar la distribución de probabilidad de las vidas de servicio y calcular los gastos de depreciación utilizando el método Probabilístico, de modo que gastos de depreciación más exactos reflejen el consumo actual de los servicios de los activos.

Apéndice 1

Definamos P_i como la probabilidad de que el activo será retirado al final del i-ésimo año. (Asumiremos que el activo sólo es retirado al final del año). Dejemos que n sea el número entero más grande i para el que P_i es positivo, de tal modo que n es la máxima vida posible del activo. Entonces, por definición,

Dejemos que h_ij sea la tasa de servicio proporcionado por el activo en su i-ésimo año en servicio respecto al servicio total proporcionado durante su vida, dado que su vida es j años. Puesto que la depreciación está basada en el consumo de los servicios del activo, h_ij también puede ser interpretado como la proporción del costo depreciable a ser depreciado en el año i-ésimo si la vida de servicio es j años. Entonces, si el servicio se distribuye uniformemente, tenemos que

mientras que si la vida de servicio declina linealmente, llegando a cero al final de su vida, tenemos el familiar método de la suma de los dígitos de los años con:

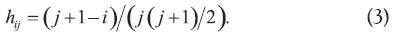
procederemos, aunque en un caso general con hij sujeto únicamente a:

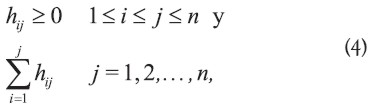
de tal modo que los resultados obtenidos tendrán el máximo nivel de generalidad.

Con los métodos convencionales, la vida esperada de un activo, L, se obtiene de

En la práctica, L se aproxima al número entero más cercano, pues muchos métodos de depreciación convencionales se determinan para vidas enteras. Con el fin de evitar complicaciones adicionales que se originen en el análisis de considerar tales efectos de aproximación, en esta sección trataremos sólo con las distribuciones de probabilidad que generan valores enteros para las vidas de servicio esperadas. Un caso más general será discutido en el apéndice 2.

Entonces, la tasa de depreciación en el año i bajo el método convencional está dada por h_iL y la depreciación acumulada al final del año k(k≤L) es

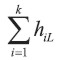
Con el método Probabilístico propuesto, la depreciación para cada año es computada para cada posible vida del activo, ponderada por la probabilidad de tal vida del activo y sumada para todas las posibles vidas del activo. Entonces, la tasa de depreciación en el año i-ésimo está dada por

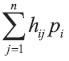
Por consiguiente, la depreciación acumulada al final de año k-ésimo (1 ≤ k ≤ n) está dada por

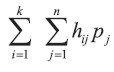
Observe que

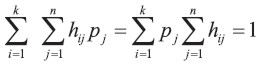
de modo que el activo estará completamente depreciado si éste dura toda su vida máxima.

Con el convencional método Determinístico, el primer año de depreciación está dado simplemente por h_iL, donde L es la vida de servicio esperada. Según el método Probabilístico propuesto, el primer año de depreciación es

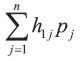
Ahora mostramos que bajo restricciones débiles y que se cumplen frecuentemente sobre h_ij, el primer año de depreciación computado por el convencional método Determinístico es siempre menor que el computado por el método Probabilístico propuesto, sea cuales sean los métodos de depreciación que son utilizados. Con el fin de obtener este resultado, necesitamos

Lema 1: (Desigualdad de Jensen)[8] Si f(x) es una función estrictamente convexa de x, entonces Ef(x) ≥ f(Ex) con igualdad sólo para el caso en el que la función de distribución de probabilidad está concentrada en un único punto.

Prueba: Si f es una función convexa de x, entonces en cada punto P=(ξ,f(x)) sobre el gráfico de f existe una línea de soporte l pasando a través de P tal que el gráfico de f está totalmente por encima de 0 en l. Por tanto, si λ es la pendiente de l tenemos que

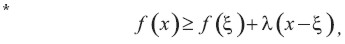
Y, por consiguiente, f(x) es una función estrictamente convexa, manteniendo la igualdad sólo para x=ξ. Con una distribución de probabilidad arbitraria en el dominio de f, elegimos ξ=E(x). Tomando la esperanza en * obtenemos Ef(x)≤f(E(x)).

Teorema 1: Si h_ij es una función estrictamente convexa de j, entonces

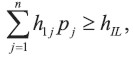
con una igualdad para las distribuciones degeneradas en las que la función de distribución de la probabilidad está concentrada en un único punto.

Prueba: Dejemos que hij sea la función que asigna el primer año de depreciación a un activo con una vida de j años. Entonces, si h_1L es una función estrictamente convexa de la variable j, tenemos del Lema 1 que

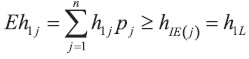
con una igualdad que se mantiene sólo si p_j =1 para cualquier j.

Notemos que para la depreciación de línea recta h_ij = 1⁄j y para la suma de los dígitos de los años h_1j = (2⁄j+1), que son convexas en j. La h_1j para el método del doble saldo decreciente es 2⁄j, que es también convexa en j.

Con el fin de obtener una mayor caracterización de la trayectoria de la depreciación acumulada bajo los métodos de depreciación Determinístico y Probabilístico, introduciremos el concepto de concavidad discreta. Una función f(j) definida sobre los enteros 0, 1, 2, ..., n, ..., es discretamente convoca si β f(j₁)+(1-β)f(j₂)≤f(βj₁+(1-β)j₂) para todo β є [0,1] donde βj₁ + (1-β)j₂ es un entero. Una condición suficiente para la concavidad discreta es que [ f(j+1) - f(j) ] - [ f(j) - f(j-1) ] = f(j+1) - 2f(j) + f(j-1)≤0 para todo j= 1, 2, ... . Esta es una versión discreta de la familiar propiedad de las primeras diferencias decrecientes de las funciones cóncavas continuas. Para nuestros propósitos, f(j) para j=0, 1, ..., n es la depreciación acumulada después de j años, aunque para j = n+1, n+2, ..., f(j)=f(n).

También necesitamos asumir que el servicio consumido en un año es función no creciente de la edad de tal modo que h_ij ≥ h_i+1 para todo i=1, ...., n. Este supuesto se satisface en la práctica con los métodos de depreciación común, como los métodos de línea recta, suma de los dígitos de los años y doble saldo decreciente.

Teorema 2: Si h_ij ≥ h_i+1 para i = 1, ...., j; j = 1, ..., n, la depreciación acumulada después de k años (1 ≤ k ≤ n) bajo el método Probabilístico,

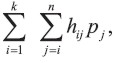
es una función discretamente cóncava de k para k = 1, 2, ...., n.

Prueba:

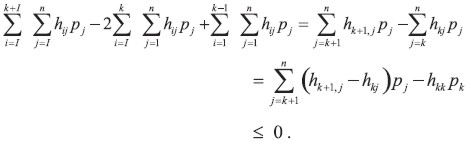
Es fácil de obtener un resultado similar para el método Determinístico como se muestra en el

Teorema 3: Si h_iL ≥ h_i+1,L para i = 1, ..., L, la depreciación acumulada después de k años (1 < k < L) bajo el método Determinístico,

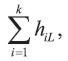
es una función discretamente cóncava de k.

Prueba:

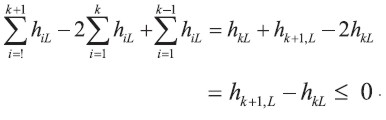
Las conclusiones de los tres teoremas permiten comparar la trayectoria de la depreciación acumulada bajos los métodos de depreciación Probabilística y Determinística, como se ilustra en la gráfica 4.

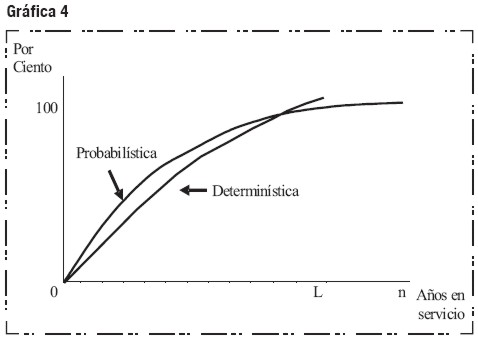
La depreciación acumulada bajo el método Probabilístico excede inicialmente la misma bajo el método Determinístico, reflejando el gasto creciente en los primeros años (teorema 1). Mientras que bajo el método Determinístico, el activo es completamente depreciado hasta el final de los L años, bajo el método Probabilístico el activo no es completamente depreciado hasta el final de n(>L) años; las dos trayectorias se intersecan en algún año menor a L. La concavidad demostrada en los teoremas 2 y 3 asegura que las trayectorias tienen la forma general indicada y que las trayectorias sólo se cruzan una vez.

En el caso de la depreciación de grupos, la tasa de depreciación para el método Probabilístico es idéntica a aquella utilizada para el caso de un solo activo. La única diferencia es que el costo depreciable está basado en todos los ítems del grupo de activo en lugar de un solo activo.

Sin embargo, el esquema para la depreciación de grupos convencional difiere, en cierto modo, del caso de un solo activo. Para la depreciación de línea recta con una vida de servicio esperada de L años, la tasa en el iésimo año está dada, como se mencionó antes, por 1⁄L. Ahora, esta tasa es aplicada sólo para aquellos activos que estuvieron en servicio al comienzo del i-ésimo año. Por consiguiente, la trayectoria de depreciación actual bajo el método de grupo convencional es una función del patrón actual de retiros que ocurra. Para propósitos de comparación, consideremos un patrón típico en el que el número actual de retiros en cada año corresponde al número esperado. En la práctica, se puede esperar que la trayectoria actual fluctúe alrededor de esta trayectoria típica.

Entonces, si comenzamos con N ítems, cada uno con un costo depreciable de C, el número esperado de ítems aún en servicio al comienzo del i-ésimo año está dado por

Por tanto, el gasto de depreciación bajo el método de línea recta Determinístico en el i-ésimo año está dado por

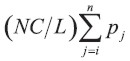
y la depreciación acumulada después de k años es

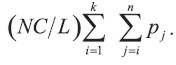
Para k = n tenemos la depreciación acumulada igual a

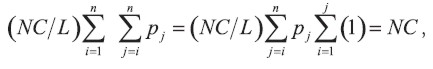
de tal modo que el grupo de activos es completamente depreciado sólo hasta el final de la vida máxima de servicio. El método utilizado en la prueba de los teoremas 2 y 3 muestra que

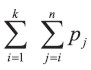
es una función cóncava de k, y sabemos por el teorema 1 que el primer año de depreciación bajo el método Probabilístico excede la misma bajo el método Determinístico. Dado que dos funciones cóncavas no idénticas sólo pueden ser iguales en dos puntos (aquí k = 0 y k = n), tenemos que

Teorema 4: Si en la depreciación de grupos bajo línea recta el número actual de retiros iguala el número esperado, la depreciación acumulada bajo el método Probabilístico es siempre mayor que la depreciación acumulada bajo el método Determinístico hasta el final de la vida máxima de servicio posible cuando la depreciación acumulada bajo ambos métodos es igual.

Apéndice 2

Activos con vida de servicio continua

A través del análisis hemos asumido que los activos únicamente son retirados al final del año. El análisis se extiende directamente a la situación en la que los activos pueden ser retirados al final de cualquier intervalo fijo, tal como un mes, seis meses, etc. En este caso, p_i es la probabilidad de que el activo sea retirado al final del i-ésimo intervalo de tiempo.

El límite de tomar intervalos de tiempo más finos y más finos puede ser conseguido al considerar un proceso de depreciación continuo en el que la vida de servicio esperada puede tomar cualquier valor sobre la recta de los reales positivos. De esta manera, incluso aunque los gastos de depreciación serían computados en intervalos de tiempo discreto, desearíamos considerar el problema de los activos con distribuciones de vida de servicio continua, de tal modo que los ítems puedan ser retirados en cualquier tiempo dentro del intervalo de tiempo. En este caso, definimos h(x,y) ≥ 0 para 0 ≤ x ≤ y como la tasa a la que la vida de servicio está siendo gastada en el punto del tiempo x, dado que la vida de servicio total es y. Normalizamos h(x,y) de tal modo que 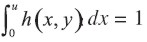. Para un activoque proporciona un servicio uniforme durante su vida de servicio h(x,y) = 1⁄y mientras que para un servicio que se deteriora linealmente h(x,y) = 2 ( 1 – x⁄y ). La depreciación acumulada en el punto del tiempo z ( 0 ≤ z≤ y) para un activo con una vida de servicio de y está dada por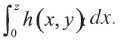

La vida se servicio ahora puede ser caracterizada por una función de densidad continua f(y), donde 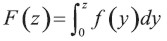es la probabilidad que la vida de servicio esperada sea menor o igual a z.

De acuerdo con estos supuestos, la depreciación acumulada en el punto del tiempo z utilizando el método de depreciación Probabilístico está dada por 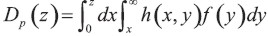. El método de depreciación Determinístico primero obtiene la vida de servicio esperada, L, de 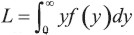y computa la depreciación con base en L. Entonces la depreciación acumulada Determinística en el punto del tiempo z está dada por:

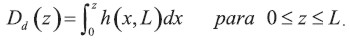
Es fácil de obtener los teoremas 1-3 equivalentes en tiempo continuo.

Teorema 1´: Si h(0, y) es una función estrictamente cóncava de y y f(y) no está concentrada en un único punto, D_p ‘(0) ≥ D_d ‘(0).

Prueba: Por la regla de Leibnitz,

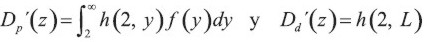
Por tanto, por la desigualdad de Jensen (Lema)

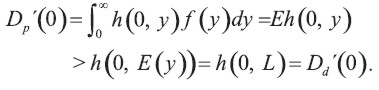
El teorema 1´ prueba que la pendiente de la depreciación acumulada utilizando el método de depreciación Probabilístico inicialmente excede la misma bajo el método Determinístico. Por conveniencia, para demostrar los teoremas 2´ y 3´ asumimos que h(x, y) es a la vez una función continuamente diferenciable de x. Por tanto, las condiciones discretas de que hij son funciones no crecientes de i para un j dado pueden ser remplazadas por la condición

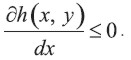
Teorema 2´ y 3´: Si h(x, y) es a la vez una función continuamente diferenciable de x con, ∂h(x,y)/∂x ≤ 0

(i) D_p(z) es una función cóncava de z

(ii) D_d(z) es una función cóncava de z

Prueba:

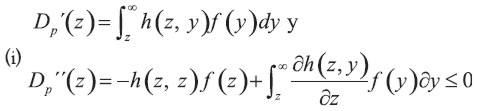
La función D_p ‘‘(z) ≤ 0 es suficiente para garantizar la concavidad de D_p(z).

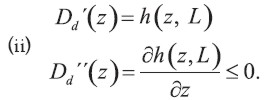
Los teoremas 1’ - 3’ muestran que para activos que se deprecian continuamente las trayectorias de la depreciación acumulada siguen el mismo patrón general como en el caso discreto.

Apéndice 3

Curvas de mortalidad del equipo físico

Edwin Kurtz[9] estudió las características de vida de 52 tipos de propiedad física incluyendo los sistemas de suministro de agua, los cables telefónicos, equipos de interruptores y postes, lámparas eléctricas y postes, vagones de ferrocarril, locomotoras y traviesas. El último trabajo (1937)[10] incluyó datos sobre automóviles y equipo de agricultura. Kurtz encontró que las curvas de mortalidad de estos diversos equipos siguieron comportamientos similares y podían ser agrupados. Finalmente, él llegó a siete curvas generales que caracterizaron las particularidades de retiro del equipo bajo estudio. Los datos para estas curvas son presentados en la tabla 7, en la que el intervalo de edad, x, es expresado como un porcentaje de la vida promedio, la columna £x presenta un porcentaje de la vida promedio y la columna dx el porcentaje de fallas durante los intervalos. Kurtz asume que las fallas en un intervalo ocurren a la mitad del intervalo, mientras en nuestros análisis hemos asumido que los retiros ocurren al final de un intervalo.

Si la vida de servicio del activo en consideración puede ser caracterizada por uno de los siete tipos de curvas, los números en la columna dx pueden ser usados para proporcionar estimaciones de las p_i requeridas por el método Probabilístico. Por ejemplo, con el tipo de curva IV, asumimos que la vida promedio es diez años e interpolamos con los puntos sucesivos para obtener estimaciones sobre las probabilidades de falla al final del año, más que a mediados. Esto genera los valores de d_i y l_i presentados en la tabla 8.

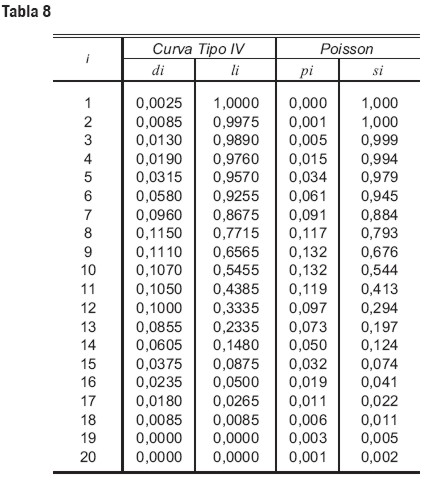
Alternativamente, podemos utilizar la distribución Poisson para proporcionar una aproximación a estas curvas de mortalidad. Continuando nuestro ejemplo, consideremos una distribución de la vida de servicio Poisson con una media de diez años. Los valores de p_i y también de s_i –la probabilidad de que el activo esté aún en servicio al comienzo del año– son presentados en la tabla 8.

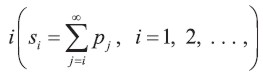
Comparando l_i con s_i vemos que el ajuste es en efecto excelente, con una desviación máxima entre las dos curvas menor a .04. Aplicando la prueba de Kolmogorov- Smirnov[11], tal desviación está dentro del 95% del intervalo de confianza de la distribución (Poisson) teórica para tamaños de muestra aproximadamente hasta de 1.200[12].

Pie de página

[1] Un concepto alternativo de depreciación consiste en reflejar la disminución en el valor de mercado del activo durante el periodo. Sin embargo, la discusión en este documento no depende de un concepto particular de depreciación: ésta sólo requiere que el concepto esté bien establecido. Por consiguiente, para propósitos ilustrativos, concentraremos nuestro análisis únicamente en el servicio potencial consumido.

[3] Un estudio de las características de la mortalidad de la propiedad física es descrita en Edwin B. Kurtz, Life expectancy of physical property (Ronald Press, 1930). El apéndice 3 resume algunos de los resultados de este estudio.

[4] De hecho, la distribución Poisson proporciona una excelente aproximación a las curvas de mortalidad descritas en Kurtz (véase apéndice 3).

[5] Puesto que la distribución Poisson es especificada por un solo parámetro, el gasto de depreciación Probabilística en cualquier año puede ser considerado como una función únicamente de la vida esperada. Esta función es, por supuesto, considerablemente más compleja que la del método Determinístico.

[5a] Para una discusión de la depreciación de grupos, ver Eugene Grant y Paul Norton, Depreciation (Ronald Press, 1949).

[6] Un método similar al propuesto en esta sección ha sido considerado antes. Ver Edwin B. Kurtz, The science of valuation and depreciation (Ronald Press, 1937); Gabriel Preinreich, “The practice of depreciation,” Econometrica, (julio, 1939); Robley Winfrey, Depreciation of group properties, (Iowa State College Bulletin 155, 1942); Gabriel Preinreich, “Review of depreciation of group properties,” the accounting review, (abril, 1944); Bradford F. Kimball, “The failure of unit-summation procedure as a group method of estimating depreciation,” Econometrica, (1945). Este método parece haber sido descartado debido al fracaso en reconocer el modelo Probabilístico subyacente. Los autores asumieron que los ítems fallarían precisamente como las curvas de mortalidad indicaban, y que por lo tanto era importante identificar con anticipación cuales ítems fallarían en cada año.

[7] Este ejemplo es tomado de Myron J. Gordon y Gordon Shillinglaw, Accounting: A management approach, Third Edition (Richard D. Irwin, Inc., 1964) pp. 350-352.

[8] Ver William Feller, An introduction to probability theory and its applications, Volume II (John Wiley and Sons, Inc., 1960) pp. 151- 152.

[9] Kurtz, Life expectancy of physical equipment.

[10] Kurtz, The science of valuation and depreciation.

[11] Paul G. Hoel, Introduction to Mathematical Statistics, Third Edition, (John Wiley and Sons, Inc., 1962) pp. 345-349.

[12] Los datos para el tipo de curva IV son un promedio de los datos de diversos equipos, puesto que es difícil obtener una estimación del tamaño muestral real utilizado al derivar la curva.