Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Innovar
versão impressa ISSN 0121-5051
Innovar v.20 n.36 Bogotá jan./abr. 2010
Juan David Velásquez Henao*, Carlos Jaime Franco Cardona**
* Escuela de Sistemas, Universidad Nacional de Colombia, sede Medellín. Correo electrónico: jdvelasq@unal.edu.co
** Escuela de Sistemas, Universidad Nacional de Colombia, sede Medellín. Correo electrónico: cjfranco@unal.edu.co
RECIBIDO: diciembre 2008 APROBADO: enero 2010
RESUMEN:
Los contratos en los mercados liberalizados de electricidad constituyen una herramienta para proteger a los agentes de la volatilidad; en este contexto, los pronósticos de los precios son una entrada clave para la toma de decisiones estratégicas y operativas de los agentes. En este artículo, se pronostican los precios promedios de los contratos despachados en el mercado eléctrico colombiano, usando una red neuronal con arquitectura dinámica conocida como DAN2. El modelo desarrollado es capaz de capturar la dinámica intrínseca de la serie de precios y de pronosticar el precio para el siguiente mes con más precisión que la metodología ARIMA clásica, para horizontes de predicción de 12 y 24 meses.
PALABRAS CLAVE:
precios de la electricidad, redes neuronales artificiales, predicción, series de tiempo.
ABSTRACT:
Contracts in unregulated electricity markets are a tool to protect the agents from volatility; in this context, price predictions are a key input to enable customers to make strategic and operational decisions. In this article, average prices are predicted for contracts signed in the Colombian electricity market, using a neuronal network with dynamic architecture known as DAN2. The model developed is able to capture the intrinsic dynamic of series of prices and forecast the price for the following month with greater precision than the classic ARIMA methodology, for forecasting horizons of 12 and 24 months.
KEY WORDS:
Electricity prices, artificial neuronal networks, prediction, time series.
RÉSUMÉ:
Les contrats dans les marchés libéralisés d'électricité sont un moyen de protection des agents de la volatilité; dans ce contexte, les pronostics de prix sont essentiels pour la prise de décisions stratégiques et opératives des agents. Dans cet article, les prix moyens des contrats fournis sur le marché électrique colombien sont pronostiqués, moyennant l'emploi d'un réseau neuronal avec architecture dynamique connue sous le nom de DAN2. Le modèle développé permet de capturer la dynamique intrinsèque de la série de prix et de pronostiquer le prix pour le mois suivant de façon plus précise que la méthodologie classique ARIMA, pour un horizon de prédiction de 12 mois et de 24 mois.
MOTS-CLEFS:
Prix de l'électricité, réseau neuronal artificiel, prédiction, séries de temps.
RESUMO:
Os contratos nos mercados liberalizados de eletricidade são uma ferramenta para proteger aos agentes da volatilidade; neste contexto, os prognósticos dos preços são uma entrada chave para a tomada de decisões estratégicas e operativas dos agentes. Neste artigo, prognostica-se a média de preços dos contratos estabelecidos no mercado elétrico colombiano, usando uma rede neural com arquitetura dinâmica conhecida como DAN2. O modelo desenvolvido é capaz de capturar a dinâmica intrínseca da série de preços e prognosticar o preço para o mês seguinte com mais precisão que a metodologia ARIMA clássica, para horizontes de predição de doze a vinte e quatro meses.
PALAVRAS CHAVE:
preços da eletricidade, redes neuronais artificiais, predição, séries de tempo.
INTRODUCCIÓN
Con la liberalización y desregulación de muchos mercados de electricidad en el mundo, el problema de predicción de precios ha cobrado una importancia singular, tanto por sus dificultades teóricas y conceptuales, como por sus implicaciones prácticas. Los precios de la electricidad se ven influidos por una gran cantidad de factores complejos relacionados con las características físicas del sistema de generación, la influencia de las decisiones de negocio de los distintos agentes, y la regulación (Velásquez et ál., 2007). De ahí que los precios presenten una dinámica cuya complejidad se manifiesta a través de características como: pronunciados ciclos estacionales de periodicidad diaria, semanal, mensual y demás; volatilidad variable en el tiempo y regiones de volatilidad similar; fuertes variaciones de año a año y de estación a estación, estructura dinámica de largo plazo, efectos de apalancamiento y respuesta asimétrica de la volatilidad a cambios positivos y negativos, valores extremos, correlaciones de alto orden, cambios estructurales, tendencias locales y reversión en la media, diferentes determinantes para los riesgos de corto, mediano y largo plazo, dependencia de las condiciones de las unidades de generación en el corto plazo y de las inversiones en capacidad y crecimiento de la demanda en el largo plazo.
La negociación de la electricidad a través de contratos se constituye un mecanismo de mitigación del riesgo al que se ven sometidos los agentes si negociaran únicamente en el mercado de corto plazo. Por una parte, evitan que el comprador se vea sujeto a la volatilidad de los precios en el mercado de corto plazo, y, especialmente, a los precios excepcionalmente altos que se pueden registrar en dicho mercado; por otra parte, estabilizan los ingresos del vendedor y lo protegen de precios excepcionalmente bajos.
Así, la predicción de los precios de la electricidad se vuelve un insumo fundamental que requieren los diferentes agentes para establecer sus políticas de comercialización, en donde se especifican las cantidades de energía vendida a través de cada uno de los mecanismos de negociación, de acuerdo con las expectativas de precios.
El mercado eléctrico colombiano establece, desde su liberalización, que la electricidad puede ser negociada en la Bolsa de electricidad o a través de contratos bilaterales entre los agentes. Existen dos tipos de contratos representativos en el mercado eléctrico colombiano: pague-lo-contratado y pague-lo-demandado. El tipo pague-lo-contratado especifica que el comprador se compromete a pagar toda la electricidad contratada, independientemente de si ella fue consumida o no; si se contrató una mayor cantidad de electricidad a la consumida, el excedente es vendido por el comprador a la Bolsa de energía. En el tipo pague-lodemandado, el comprador sólo paga la energía efectivamente consumida; usualmente, se fija un límite superior a la energía que puede ser consumida por el comprador.
Ya que los agentes requieren la predicción de los precios de la electricidad como un insumo fundamental para realizar sus procesos decisorios, tanto operativos como estratégicos, y que las series de precios presentan características complejas que dificultan el desarrollo de modelos de predicción, se hace necesaria la investigación sobre esta problemática.
En la literatura ya se han reportado experiencias sobre el pronóstico de series de precios de la electricidad usando redes neuronales artificiales, y particularmente, usando perceptrones multicapa (MLP, por su sigla en inglés). No obstante, el uso de MLP presenta varios problemas. Primero, la estimación de los parámetros se basa en la minimización del riesgo empírico, que es equivalente a minimizar el error de ajuste a los datos disponibles; para ello, se parte de la estructura del modelo como un parámetro de entrada que debe ser predefinido de antemano; más aún, la especificación de los MLP se basa fundamentalmente en criterios heurísticos y el juicio experto del modelador (Masters, 1993 y 1995), de tal manera que dicho proceso se basa en un conjunto de pasos críticos que afectan el desempeño final del modelo (Kaastra y Boyd, 1996), en términos del ajuste a los datos históricos y su capacidad de generalización; esto dificulta enormemente la reconstrucción del proceso de especificación y selección de esta clase de modelos. Segundo, los MLP se caracterizan por poseer múltiples puntos de mínima local, por lo que nunca puede garantizarse que se haya obtenido el modelo con el menor error de ajuste posible para una configuración determinada. Tercero, la complejidad de la red neuronal debe ser definida por el modelador. Zhang et ál. (1998) han hecho una revisión extensa sobre la predicción de series de tiempo usando redes neuronales artificiales.
Ghiassi y Saidane (2005) presentan un nuevo tipo de red neuronal de arquitectura dinámica, llamado DAN2, que difiere considerablemente de los modelos tradicionales de propagación hacia adelante. Ghiassi et ál. (2005) pronostican seis series que han sido utilizadas por diferentes investigadores como un benchmark para comparar la precisión de varios modelos no lineales; según los resultados reportados por dichos autores, DAN2 puede alcanzar errores de ajuste y de predicción muy inferiores a los obtenidos con técnicas más tradicionales, como los MLP y la aproximación ARIMA. Ghiassi et ál. (2006) aplicaron exitosamente DAN2 para realizar el pronóstico de la demanda mensual, trimestral y anual de electricidad de la compañía de potencia de Taiwán para un horizonte de mediano plazo; los autores concluyen que el modelo es más preciso que otras aproximaciones que incluyen la metodología ARIMA y otros modelos de redes neuronales. Gómez et ál. (2006) utilizaron la combinación de los pronósticos de DAN2 y de un modelo ARIMA para pronosticar varias series benchmark, y argumentan que dicha combinación produce pronósticos más precisos que cada uno de los modelos en forma separada.
Así, las experiencias reportadas sugieren que DAN2 también podría ser más preciso que los MLP y los modelos ARIMA para pronosticar los precios de la electricidad.
El objetivo de este artículo es presentar los resultados obtenidos al pronosticar la serie de precios promedios mensuales de contratos despachados en la Bolsa de Energía de Colombia, usando DAN2 y un modelo ARIMA (Box y Jenkins, 1970), y determinar cuál de dichas aproximaciones permite obtener pronósticos más precisos. En este caso se considera únicamente modelos univariados, ya que no hay estudios que permitan relacionar los precios de los contratos con variables físicas o económicas del mercado de electricidad, ni con la serie de precios de Bolsa. Una presentación profunda sobre el modelo ARIMA, sus propiedades y su proceso de especificación es realizada por Makridakis et ál. (1998).
La originalidad e importancia de la investigación propuesta está basada en los siguientes aspectos:
- Mientras que existe una extensa experiencia en la predicción de precios de electricidad en mercados de corto plazo (ver el trabajo de Velásquez et ál., 2007), no existen referencias en la literatura sobre la predicción de precios de contratos. Sobre este aspecto se da la primera contribución de este artículo, ya que se pretende desarrollar varios modelos de pronóstico para dicha serie.
- La motivación de este artículo surge desde la práctica: la necesidad que tienen los agentes de contar con pronósticos de los precios de la electricidad. En este artículo se busca evaluar si es posible utilizar modelos no lineales para el pronóstico de la serie de precios, de tal manera, que sus resultados son una clara señal para la continuación de esta investigación incorporando nuevas metodologías. Debe aclararse, que esta investigación no se centra en los aspectos rigurosos y formales propios del análisis econométrico, sino en los aspectos empíricos de la predicción como un insumo para la toma de decisiones, donde prima la capacidad para obtener el pronóstico más preciso posible dejando a un lado los aspectos más formales.
- No existen experiencias reportadas en la literatura que comparen el desempeño del modelo DAN2 con otros modelos al pronosticar series de precios de electricidad. La serie analizada en esta investigación es particularmente.
- Se contribuye a difundir el uso de DAN2 para la predicción de series de precios en mercados de electricidad, aumentando así la cantidad de herramientas disponibles.
El resto de este artículo está organizado como se indica a continuación. En la sección 2, se examina la formulación matemática de DAN2. En la sección 3, se reportan los resultados obtenidos usando DAN2 y se comparan con los resultados obtenidos usando un modelo ARIMA. En la última sección se presentan las conclusiones.
INFORMACIÓN y METODOLOGÍA
Información utilizada
Los datos con que se elaboró este estudio corresponden al logaritmo natural de la serie de precios mensuales promedio de los contratos despachados en la Bolsa del mercado mayorista de electricidad en Colombia, expresada en $/kWh, entre mayo de 1996 y junio de 2008, los cuales están disponibles en el sistema Neón.
Esta serie es calculada como el promedio de los precios pactados en los contratos en ejercicio durante cada mes, ponderados por la cantidad de energía negociada en cada contrato; cabe anotar, que el precio pactado en cada contrato es privado, y por tanto, los agentes del sistema no tienen acceso a este valor. Consecuentemente, la serie en estudio se constituye como la única señal directamente visible para todo el mercado sobre este indicador. Por otra parte, la cantidad de electricidad negociada en contratos corresponde hasta en un 80% del total de la producción de los agentes generadores en el mercado, los cuales dejan el porcentaje restante para maniobrar en la Bolsa de Energía.
La dinámica de la serie es bastante compleja, lo que puede ser explicado en el hecho de que los contratos en ejercicio para una hora determinada del mes varían en muchos aspectos (Dyner, Franco y Arango, 2008):
- La cantidad de energía liquidada al final del contrato: pague-lo-contratado, pague-lo-demandado, pague-lodemandado-con-tope.
- El mecanismo para calcular los precios: un único precio fijo para todo el contrato, precio horario fijo, precio amarrado al precio de Bolsa, precio indexado, inclusión de topes máximo y mínimo para el precio del contrato.
- El momento en que fueron firmados los contratos en ejercicio: desde unos pocos meses hasta diez años atrás. No obstante, existe una clara tendencia a que el plazo de los contratos no supere los dos años.
La serie (figura 1) presenta una tendencia creciente de largo plazo desde mayo de 1996 hasta el primer semestre de 2003; durante ese mismo intervalo de tiempo se evidencia una componente cíclica de periodicidad anual de amplitud variable, explicada, posiblemente, por el ciclo invierno-verano. La mayor amplitud de la componente periódica coincide con el fenómeno de El Niño ocurrido entre los años 1997 y 1998; esta componente cíclica, aunque no con una amplitud tan marcada, permanece hasta principios del año 2004. Desde el año 2003 se presenta una tendencia ligeramente descendente que finaliza en algún momento del primer semestre del año 2006. Se evidencia en este momento del tiempo un cambio estructural en la serie, tanto en su tendencia como en su componente cíclica; por una parte, se recuperan los niveles de crecimiento que caracterizaron los años 2000, 2001 y 2002, mientras que, por la otra, se presenta nuevamente un ciclo estacional de periodo anual, cuyo nivel más alto coincide con la estación de verano.
Metodología empleada
La arquitectura de DAN2 y su proceso de entrenamiento son completamente presentados por Ghiassi y Saidane (2005). Al igual que otros tipos de redes neuronales, DAN2 tiene una capa de entrada y varias capas de procesamiento; la salida del modelo es el resultado de la última capa; un diagrama esquemático se presenta en la figura 2. I representa las entradas al modelo, y corresponde a los rezagos de la serie de tiempo usados como predictores. El primer nodo oculto, F0, corresponde a la combinación lineal de las entradas más un término constante; esto equivale, en nuestro caso, a construir el modelo autorregresivo:
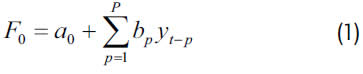
La k-ésima capa oculta, para k = 1,...,K, está conformada por cuatro nodos: un nodo constante C de salida unitaria, la cual es ponderada por el peso ak; un nodo CAKE (current accumulated knowledge element) que recibe la salida de la capa anterior, Fk-1, ponderada por el peso bk. Y dos nodos CURNOLE (current residual nonlinear element) notados como Gk y Hk, respectivamente; estos nodos realizan una transformación no lineal del patrón de entrada a la red neuronal. Así, la salida de la k-ésima capa de procesamiento para el patrón de entrada Xi, que contiene los rezagos yt-1,..., yt-P es:
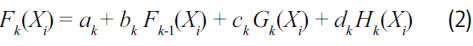
Los nodos Gk y Hk se encargan de capturar la componente no lineal remanente en los datos, a partir de su proyección vectorial. Para ello, se define un vector aleatorio R de P componentes, y se proyecta sobre este vector cada conjunto de regresores, Xi. Esta proyección define un ángulo αi para cada conjunto de regresores Xi. El proceso es explicado en detalle por Ghiassi y Saidane (2005). La transformación se realiza al considerar que Gk(Xi) = cos(mk*α i) y que Hk(Xi) = sen(mk*αi).
El proceso de estimación se basa en encontrar los valores de los parámetros a0, b0, ak, bk, ck, dk y mk que minimizan el error entre la serie real y la salida del modelo.
RESULTADOS OBTENIDOS Y DISCUSIÓN
Tal como se indicó, la muestra utilizada corresponde al logaritmo natural de la serie de precios medios mensuales de los contratos despachados en la Bolsa del mercado mayorista de electricidad en Colombia, expresada en $/kWh, entre mayo de 1996 y junio de 2008. La serie consta de 146 observaciones, de las cuales las primeras 122 son usadas para la estimación de los parámetros de todos los modelos, y las siguientes 24 para evaluar su capacidad de generalización y pronóstico. Con el fin de determinar la capacidad de generalización para distintos horizontes de tiempo, se usaron dos muestras de pronóstico: la primera consta de 12 observaciones (entre julio de 2006 y junio de 2007), y la segunda de 24 observaciones (entre julio de 2006 y junio de 2008). Los horizontes de predicción seleccionados son especialmente difíciles de pronosticar, ya que vuelve a aparecer un patrón cíclico anual que había desaparecido desde el año 2003, y porque en el punto donde se inicia la muestra de predicción se presenta, aparentemente, un cambio de tendencia en la serie.
La bondad del ajuste fue medida mediante la sumatoria del error cuadrático medio (SSE, por su sigla en inglés) de los residuos, et:
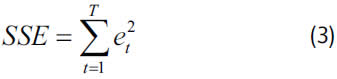
y su desviación media absoluta (MAD, por su sigla en inglés):
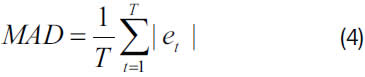
En primera instancia se desarrolló un modelo ARIMA. Dado que la serie presenta una componente de tendencia de largo plazo y un patrón cíclico de periodicidad anual, se aplicaron los operadores de diferenciación simple (1-B), y estacional (1-B12). B es el operador de rezago, tal que Byt = yt-1. Para la serie obtenida se construyeron modelos autorregresivos de orden P, con P = 1,..., 12. Los estadísticos de ajuste a la muestra de entrenamiento (calibración) y a las muestras de predicción, para:
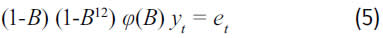
donde φ(B) es el modelo autorregresivo de orden P, son reportados en la tabla 1. El modelo ARIMA-12 presenta el mejor ajuste a la muestra de calibración; no obstante, su precisión es de menor calidad respecto a otros modelos de diferente orden. Los modelos ARIMA-3 y ARIMA-4 presentan los mejores estadísticos para la predicción con horizontes de 1 y 2 años, pero sus SSE a la muestra de entrenamiento son más del doble que el mejor ajuste obtenido para un modelo ARIMA. El modelo ARIMA-12 presenta el mejor ajuste global; el SSE total para la muestra de calibración y los horizontes de predicción de 1 y 2 años son de 0,084 y 0,093, respectivamente.
Para hacer comparable la información utilizada por DAN2 respecto al modelo ARIMA, se expandió la ecuación (5) y se incluyeron todos los rezagos involucrados. Así, (1-B)(1-B12)φ(B)=(1-B-B12-B13)φ(B); sabiendo que φ(B) es un polinomio de orden P que incluye los términos desde B hasta BP, es fácilmente demostrable que el modelo contendría información para los rezagos 1,..., min{ 12, P+1}, 13, ..., P+13. De esta forma para P = 1, los rezagos involucrados serían 1, 2, 13, 14. El modelo DAN2 fue estimado considerando los rezagos obtenidos para P = 1, ...,12. Los resultados obtenidos se presentan en la tabla 1.
El modelo DAN2-11 presenta los mejores estadísticos de ajuste a la muestra de entrenamiento; sin embargo, su capacidad para pronosticar la serie por fuera de la muestra de calibración es muy pobre, y es superado por modelos con otras entradas. El modelo DAN2-3 presenta el mejor ajuste a la muestra de pronóstico con un horizonte de 12 meses, pero tiene un desempeño muy bajo en el ajuste a la muestra de calibración, ya que su SSE es más de 6 veces el obtenido por el modelo DAN2-11. Si se considera simultáneamente la precisión de cada modelo al pronosticar la muestra de calibración y las muestras de validación, se encuentra que el modelo DAN2-10 es el más preciso con unos SSE de 0,039 y 0,058 para los horizontes de 1 y 2 años, respectivamente.
Al comparar DAN2 y la aproximación ARIMA, se encuentra que varias configuraciones de DAN2 superan la precisión obtenida por el modelo ARIMA-12. Particularmente, el SSE para el modelo DAN2-11 se reduce en un 79% respecto al modelo ARIMA-12. En relación con el desempeño global de cada modelo, se producen unas reducciones del 51% y del 37% al considerarse el desempeño de los modelos ARIMA-12 y DAN-10 para los horizontes de 12 y 24 meses, respectivamente.
Los resultados indican, de forma indirecta, que la dinámica de la serie es no lineal, y que el modelo utilizado (DAN) captura adecuadamente su dinámica respecto a la aproximación ARIMA.
CONCLUSIONES
En este artículo se pronostican los precios promedios de los contratos despachados en el mercado colombiano, usando una red neuronal con arquitectura dinámica conocida como DAN2. Los pronósticos obtenidos son contrastados con los obtenidos usando la metodología ARIMA. El modelo DAN2 preferido es capaz de capturar la dinámica intrínseca de la serie de precios y de pronosticar el precio para el siguiente mes con más precisión que la metodología ARIMA clásica, para horizontes de predicción de 12 y 24 meses. Este resultado confirma que los precios poseen una dinámica no lineal que no puede ser capturada por el modelo ARIMA.
REFERENCIAS BIBLIOGRÁFICAS
Box, G. E. P. & Jenkins, G. M. (1970). Time Series Analysis: Forecasting and Control. San Francisco: Holden-Day Inc. [ Links ]
Dyner, I., Franco, C. J. & Arango, S. (2008). El mercado mayorista de electricidad colombiano. Medellín: Universidad Nacional de Colombia. [ Links ]
Ghiassi, M. & Saidane, H. (2005). A dynamic architecture for artificial neural networks. Neurocomputing, 63, 397-413. [ Links ]
Ghiassi, M., Saidane, H. & Zimbra, D. K. (2005). A dynamic artificial neural network model for forecasting time series events. International Journal of Forecasting, 21, 341-362. [ Links ]
Ghiassi, M., Zimbra, D. K. & Saidane, H. (2006). Medium term system load forecasting with dynamic artificial neural network model. Electric Power Systems Research, 76, 302-316. [ Links ]
Kaastra, I. & Boyd, M. (1996). Designing a neural network for forecasting financial and economic series. Neurocomputing, 10, 215-236. [ Links ]
Makridakis, S. G., Wheelwright, S. C. & Hyndman, R. J. (1998). Forecasting: Methods and applications (3a. ed.). New York: John Wiley & [ Links ] Sons.
Masters, T. (1993). Practical Neural Network Recipes in C++ (1a. ed.). New York: Academic Press, Inc. [ Links ]
Masters, T. (1995). Neural, Novel and Hybrid Algorithms for Time Series Prediction (1a. ed.). New York: John Wiley and Sons, Inc. [ Links ]
Gómez, G. S. S., Maia, A. L. S., Ludermir, T. B., Carvalho, F. & Araújo, A. F. R. (2006, July). Hybrid model with dynamic architecture for forecasting time series. Proceedings of the International Joint Conference on Neural Networks. Vancouver, Canada. [ Links ]
Velásquez, J. D., Dyner, I. & Souza, R. C. (2007). ¿Por qué es tan difícil obtener buenos pronósticos de los precios de la electricidad en mercados competitivos? Cuadernos de Administración, 20(34), 259-282. [ Links ]
Zhang, G., Patuwo, B. & Hu, M. (1998). Forecasting with artificial neural networks: the state of the art. International Journal of Forecasting, 14, 35-62. [ Links ]














