Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Innovar
Print version ISSN 0121-5051
Innovar vol.21 no.41 Bogotá Sept./Dec. 2011
Sergio Zúñiga-Jara*, Karla Soria** & Oscar Sjoberg***
* Doctor en Finanzas, Universidad Católica del Norte, Coquimbo, Chile Correo-e: sz@ucn.cl
** Doctor en Administración, Universidad Católica del Norte, Coquimbo, Chile Correo-e: ksoria@ucn.cl
*** Doctor en Administración, Universidad Arturo Prat, Iquique, Chile Correo-e: oscar.sjoberg@unap.cl
Recibido: diciembre de 2009 Aprobado: mayo de 2011
Resumen:
El estudio incluye una introducción, en la que se definen el modelo y los supuestos básicos. A partir de estos se obtiene una serie de resultados aplicables en la valoración de empresas, con implicancias en la evaluación de proyectos. El trabajo concluye con una ilustración numérica. Los autores sostienen que resultados conocidos de la teoría de la estructura óptima de capital, pueden ser adaptados y aplicados en la evaluación de proyectos. Esto permite aclarar aspectos clave de la evaluación privada de proyectos sobre los cuales en Latinoamérica parece existir alguna confusión. Un primer resultado es que el valor actual neto (VAN) es en realidad un concepto muy preciso y concreto, aun cuando el proyecto haya sido financiado con una mezcla de deuda y patrimonio. Un segundo resultado es que el VAN puede ser formulado de varias formas equivalentes, en el sentido de que su cálculo final es idéntico.
Finalmente, se muestra que el punto de vista usado en la evaluación de proyectos no es relevante para estimar el VAN.
Palabras clave:
costo del capital, evaluación de proyectos, WACC, valor actual neto.
Abstract:
The study includes an introduction, in which the model and basic suppositions are defined. Based upon them, a series of results is obtained which are applicable in assessing companies, with implications in the evaluation of projects. The work concludes with a numerical illustration. The authors maintain that the results in the theory of optimal structure of capital can be adapted and applied in evaluating projects. This makes it possible to clarify key aspects in the private evaluation of projects regarding which there appears to be some confusion in Latin America. The first result is that Current Net Worth (CNW) is in reality a very precise and concrete concept, even when the project has been financed through a mixture of debt and equity. A second result is that the CNW can be formulated in various equivalent ways, in the sense that the final calculation is identical.
Finally, the point of view used in evaluating projects is shown to be irrelevant in calculating the CNW.
Keywords:
Cost of capital, evaluation of projects, WACC, Current Net Worth.
Résumé :
Cette étude commence par une introduction définissant le modèle et les questions fondamentales. Ã partir de là, une série de résultats applicables dans l'évaluation des entreprises sont obtenus, impliquant également l'évaluation de projets. Le travail présente comme conclusion une illustration numérique. Les auteurs considèrent que les résultats connus de la théorie de la structure optimum de capital peuvent être adaptés et appliqués dans l'évaluation de projets. Ceci permet de préciser des aspects importants de l'évaluation privée de projets pour lesquels il existe une certaine confusion en Amérique latine.
Comme premier résultat la Valeur Actuelle Nette (VAN) est en réalité un concept précis et concret, même si le projet a été financé par un mélange de dette et de patrimoine. Comme deuxième résultat la Valeur Actuelle Nette (VAN) peut être formulée de plusieurs façons équivalentes, ce qui signifie que le calcul final est identique.
Finalement, il est démontré que le point de vue utilisé dans l'évaluation de projets n'est pas indispensable pour une estimation de la Valeur Actuelle Nette (VAN).
Mots-clefs :
coût du capital, évaluation de projets, WACC, Valeur Actuelle Nette.
Resumo:
O estudo inclui uma introdução, na qual se definem o modelo e as hipóteses básicas. A partir disso obtêm-se uma série de resultados aplicáveis na avaliação de empresas, com implicações na avaliação de projetos. O trabalho é concluído com uma ilustração numérica. Os autores sustentam que resultados conhecidos da teoria da estrutura ideal de capital podem ser adaptados e aplicados na avaliação de projetos. Isso permite aclarar aspectos chave da avaliação privada de projetos sobre os quais, na América Latina, parece existir alguma confusão. Um primeiro resultado é que o Valor Presente Líquido (VPL) é , na realidade, um conceito muito preciso e concreto, qinda quando o projeto tenha sido financiado com uma combinação de dívida e patrimônio. Um segundo resultado é que o VPL pode ser formulado de várias formas equivalentes, no sentido de que seu cálculo final é idêntico.
Finalmente, mostra-se que o ponto de vista usado na avaliação de projetos não é relevante para estimar o VPL.
Palavras chave:
Custo do capital, avaliação de projetos, WACC, Valor Presente Líquido.
En la evaluación de proyectos de empresas privadas, se sugiere normalmente usar el criterio del valor actual neto (VAN) como una medida económica de conveniencia. El consenso en la recomendación del uso del VAN se encuentra bien fundamentado en la mayoría de los principales libros de texto de finanzas (por ejemplo Ross et al., 1999; Brealey y Myers, 1998; Emery y Finnerty, 2000 y Copeland y Weston, 1988). Para tomar las decisiones de inversión, el procedimiento que generalmente se sugiere seguir consta de tres pasos: proyectar los flujos de fondos provenientes del proyecto, estimar la tasa de descuento (es decir el costo promedio ponderado del capital, WACC), y finalmente estimar el VAN usando la definición correcta de flujos y tasas. Bajo el supuesto de que las empre sas y proyectos se financian solo con deuda y con patrimo nio, la literatura también proporciona una definición estándar de flujos y tasas de descuento, como se indica a continuación:
a) Los flujos de fondos apropiados para presupuestos de capital del periodo n, representados por Fn, vienen dados por los ingresos proyectados por las ventas (Vn), menos los costos de operación (COn), depreciaciones (Depn) e impuestos corporativos a la tasa marginal t. Con esto se obtiene la utilidad después de impuestos o utilidad neta. Finalmente se suma la depreciación (para reflejar el beneficio tributario de la misma), y se restan inversiones y reinversiones (Reinvn), las que, entre otras, incluyen las necesidades de capital de trabajo (ver Cap. 7 de Ross et al.). Es decir:
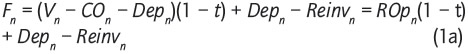
Un aspecto fundamental de la ecuación (1a), y que no es siempre notado claramente, es que no se incluyen intereses y amortizaciones por el servicio de la deuda. Dicho de otro modo, el flujo estándar para la evaluación de presupuestos de capital contiene solamente flujos operacionales, ROpn después de impuestos, ajustado por las reinversiones netas, Depn - Reinvn.
b) La tasa de descuento o tasa de costo del capital[2] es también definida de un modo estándar en la literatura (ver Cap. 12 de Ross et al.), y viene dada por la ecuación (1b):
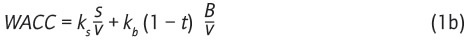
donde ks es la tasa de costo del patrimonio, la que es estimada generalmente a través del CAPM[3] de Sharpe (1974) y Black (1972), kb es la tasa de costo de mercado de la deuda. Puesto que el valor de la empresa (V) es la suma de la deuda y del patrimonio (V = B + S), entonces, 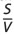 y
y 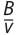 corresponden a las proporciones (a niveles objetivo de largo plazo y a valores de mercado), de patrimonio (S) y de deuda (B), respectivamente.
corresponden a las proporciones (a niveles objetivo de largo plazo y a valores de mercado), de patrimonio (S) y de deuda (B), respectivamente.
Una de las observaciones clave aquí es que, independiente de cómo se financien puntualmente los nuevos proyectos, la literatura recomienda usar siempre la definición de flujos y de tasa de descuento de las ecuaciones (1a) y (1b), respectivamente. De la literatura también se deduce que variaciones en el valor de la ecuación (1b) son esporádicas, en el sentido de que esta tasa permanece relativamente estable en el tiempo: es decir, una vez estimada, puede usarse la misma tasa para evaluar cualquier decisión de inversión, con el único requisito de que esta no posea un riesgo operacional o financiero considerablemente distinto del de la empresa.
Con esto, la fórmula también estándar del valor de una empresa viene dada por:

y el VAN de un proyecto de n periodos se resume en la siguiente expresión:
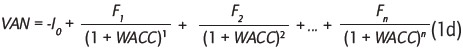
donde I0 es la inversión inicial total requerida, independiente de si es aportada por acreedores o accionistas.
A pesar del consenso en la literatura financiera respecto a lo expuesto, los autores del presente documento han notado que en Latinoamérica se postulan visiones diferentes. Específicamente, se refieren a la distinción que algunos autores hacen de la llamada evaluación económica y la evaluación financiera, donde se separa los flujos de los proyectos en flujos puros y flujos financiados. Por ejemplo, en el texto de Sapag y Sapag (2000, capítulo 4, p. 271) una vez descrita la estructura de los flujos de fondos estándar anteriormente expuesta, se señala a continuación que, alternativamente: "... si se quiere medir la rentabilidad de los recursos propios, deberá agregarse el efecto del financiamiento para incorporar el impacto del apalancamiento de la deuda". Dichos autores plantean entonces que existen dos esquemas diferentes de evaluación, en el sentido de que probablemente llevarán a resultados distintos respecto al VAN. Ellos postulan que la diferencia radica en que existe una medida de la rentabilidad de toda la inversión pero sin considerar la deuda, y una evaluación distinta para medir la rentabilidad de los recursos propios de los inversionistas, es decir desde el punto de vista de su patrimonio.
Muchos estudiantes y profesionales se preguntan si realmente existen diferentes enfoques, y hasta qué punto estos enfoques son coherentes. En opinión de los autores de esta investigación, este punto requiere una discusión y clarificación, y de aquí surge la motivación de este trabajo.
A continuación se establecen cuatro supuestos fundamentales, que si bien se encuentran implícitos en la literatura estándar de finanzas corporativas, los autores estiman que se requieren su explicitación y discusión. Como se verá, estos supuestos[4] permitirán desarrollar más adelante una serie de aclaraciones conceptuales básicas para una adecuada evaluación de proyectos.
Supuesto 1: Las empresas realizan una valuación privada, a tasas de mercado
En este supuesto se establece que los nuevos proyectos son evaluados por corporaciones privadas con fines de lucro, las que obtienen todo su financiamiento en el mercado, a tasas competitivas.
El concepto puede resumirse en señalar que se trabaja en el marco de las finanzas corporativas, es decir, de sociedades privadas con fines de lucro, y se excluyen del análisis los emprendimientos que busquen un objetivo distinto a la maximización de la riqueza de los propietarios. También se excluye la evaluación social de proyectos en el sentido de Fontaine (1999), debido a que en estos casos los proyectos deben evaluarse a una tasa de descuento social, distinto del WACC, y además, tampoco se consideran allí precios de mercado o precios privados, sino precios sombra o precios sociales.
Por otra parte, este supuesto establece que la valoración de activos se realiza a tasas de mercado, lo que implica asumir eficiencia en los mercados de instrumentos de deuda y de títulos accionarios. Esto tiene muchas implicancias deseables, como por ejemplo la inexistencia de posibilidades de arbitraje y la existencia de un único precio para un título. En resumen, indica que se puede creer en los precios de estos títulos financieros, puesto que estos reflejan toda la información relevante.
Supuesto 2: Las empresas poseen una estructura de financiamiento óptima de largo plazo, y no desean apartarse sustancialmente de ella. En adición, los nuevos proyectos son de un riesgo operacional similar al de la empresa
La existencia de una estructura de capital (o de endeudamiento) óptima para las empresas ha sido tema de largo debate en finanzas. A partir de los trabajos pioneros de Modigliani y Miller (1958 y, 1963), es generalmente aceptado que existen varias razones para evitar altos niveles de patrimonio o altos niveles deuda, con el objeto de maximizar el valor de la empresa. Entre estos factores se mencionan generalmente los costos de quiebra, costos de agencia, impuestos, asimetrías de información, entre otros (Harris y Raviv, 1991; Graham y Harvey, 2001; MacKay y Phillips, 2005).
Al existir una estructura óptima de capital, las empresas la encuentran y tratan de mantenerla en el largo plazo, sin efectuar cambios radicales año tras año en la misma. Como consecuencia, las empresas tratarán de financiar sus nuevos proyectos con dicha estructura objetivo. Sin embargo, si eventualmente un proyecto es financiado completamente con deuda o completamente con patrimonio, desviando temporalmente a la empresa de su endeudamiento óptimo, dicha decisión obligará a que el financiamiento de los siguientes proyectos apunte a recuperar el nivel de endeudamiento objetivo. Luego, la decisión de financiamiento de un proyecto en particular no puede ser considerada de forma aislada, y en cambio debe tener presente el impacto que significará en la forma de financiar los proyectos posteriores, para poder regresar a la estructura objetivo.
Por otro lado, se asume que los nuevos proyectos poseen riesgo operacional similar al de la empresa. Lo anterior significa que estos son evaluados para ser implementados por una empresa en marcha típica del sector industrial al cual pertenece el proyecto; es decir, el proyecto no aleja a la empresa de sus actuales niveles de riesgo operacional. Si bien es factible que una empresa efectúe un proyecto de un sector distinto, esto implica realizar una serie de ajustes, especialmente en la tasa de descuento, ya que tanto el riesgo operacional como el riesgo financiero son generalmente distintos para distintos sectores industriales. La corrección clásica se basa en la llamada ecuación de Hamada (1972).
En resumen, este supuesto establece que tanto el riesgo financiero como el riesgo operacional de la empresa se mantienen estables al implementar nuevos proyectos. Las implicancias finales en este supuesto son dos. Por una parte, se justifica el uso de la definición estándar del WACC en la ecuación (1b) para todos los nuevos proyectos (pues no alejan a la empresa de su estructura de endeudamiento objetivo de largo, ni de su riesgo operacional), y por otra parte, que para todos los nuevos proyectos se usará en la ecuación (1b) la estructura de financiamiento objetivo de la empresa, 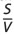 y
y 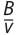 , y no la estructura de financiamiento de un proyecto en particular.
, y no la estructura de financiamiento de un proyecto en particular.
Supuesto 3: La empresa y sus proyectos generan flujos constantes y perpetuos[5]
Asumir flujos constantes y perpetuos introduce una simplificación fundamental, originalmente propuesta por Modigliani y Miller (1958 y, 1963). Esto se debe a que la estructura de estos flujos se transforma en perpetuidades, y que el valor presente de un flujo perpetuo X a la tasa i, es X/i, con lo que se logra reducir notablemente la dificultad de los cálculos de las capitalizaciones.
Existen dos implicancias en el hecho de que las empresas mantengan un nivel de operación y de endeudamiento constantes a través del tiempo:
a) Para que la empresa/proyecto siga en funcionamiento a perpetuidad, se debe reinvertir en cada periodo un monto exactamente igual a lo que se han depreciado los activos. Es decir, las reinversiones netas son cero, de modo que en la ecuación (1a) se cumple que Dep - Reinv = 0.
b) Para que la empresa mantenga un mismo nivel de endeudamiento a perpetuidad, cada vez que se amortiza parte de la deuda, inmediatamente se pide un nuevo crédito igual al monto amortizado. Con esto, en términos netos las empresas solo pagarán los intereses por la deuda, y el principal nunca se amortizará (existe un roll-over perpetuo sobre la deuda). Visto de otro modo, esto equivale a pensar en que la empresa emite un bono perpetuo (consol bond).
Por simplicidad es conveniente ampliar este supuesto haciendo que las utilidades retenidas de cada periodo sean cero, es decir que se reparten las utilidades de cada periodo a los accionistas en la forma de dividendos.
Resultados para la valoración de empresas
A partir de los supuestos establecidos anteriormente, se muestran a continuación los resultados estándar del modelo de Modigliani-Miller para valoración de empresas.
Las empresas (y los proyectos) generan un flujo total de efectivo periódicamente, denotado por FV. Este flujo es repartido entre los acreedores o tenedores de la deuda de la empresa (FD), y residualmente para los accionistas[6] o tenedores del patrimonio (FS), de modo que: FV = FS + FD. Bajo los supuestos anteriores, lo que efectivamente obtienen acreedores y accionistas se explica a continuación.
a) Por el supuesto 3, los acreedores no obtienen ninguna amortización neta del capital de la deuda, de modo que obtienen cada periodo los intereses, FD = kdD, siendo kd la tasa del costo nominal de la deuda, y D el valor libro o nominal de la deuda.
b) También por el supuesto 3, las reinversiones netas son cero, Dep - Reinv = 0, y el flujo de los accionistas es lo que queda del flujo operacional una vez deducidos los intereses por la deuda y los impuestos, es decir Fs = (ROp - kdD) (1-t). Nótese que este flujo de los accionistas corresponde a la utilidad contable neta.
Con esto, el flujo de la empresa viene dado por:
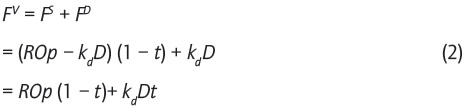
La relación de igualdad en la ecuación (2) se debe mantener cuando estos flujos perpetuos se capitaliza n a valores presentes a las tasas de descuento apropiadas. El uso de las tasas de descuento correctas está asegurado por el cumplimiento del supuesto 1.
Para actualizar los flujos de la deuda, los acreedores usarán la tasa de descuento (de mercado) dada por kb, y para los flujos perpetuos del patrimonio, los accionistas usarán la tasa ks. Nótese que estas tasas son las mismas de la ecuación (1b). Nótese también que el flujo perpetuo de la deuda es descontado a la tasa riesgosa de mercado, kb, y no a la tasa nominal kd, y que con esto, el valor presente de la deuda es: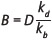 .
.
Finalmente, la capitalización del flujo total de la empresa a la tasa apropiada debe corresponder al valor de la empresa, es decir:
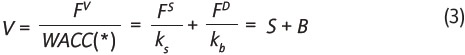
Esta expresión es la equivalente a la ecuación (1c), pero bajo el cumplimiento del supuesto 3, con un poco de álgebra a partir de la ecuación (3) puede obtenerse que la tasa de descuento apropiada para actualizar el flujo total de la empresa es el costo del capital promedio ponderado, aunque expresado antes de impues tos, es decir:

Las ecuaciones (2), (3) y (4) entregan una definición consistente de flujos y tasas para valorar empresas. Esto debería ser suficiente para obtener una serie de implicancias útiles para evaluación de proyectos; sin embargo, la disciplina financiera ha establecido algunos ajustes o correcciones útiles. En efecto, de la derivación anterior puede apreciarse una diferencia, tanto en la definición de flujo de fondos estándar (ecuación 1a vs. ecuación 2), como en la tasa de descuento (ecuación 1b vs. ecuación 4). Para el caso de los flujos, se obtiene FV = ROp(1 - t) + kdDt en lugar de F = ROp(1 - t), ya que se anulan los últimos sumandos de la ecuación (1a) al existir flujos perpetuos (ver tabla 1). La diferencia entre FV y F radica en el término kdDt, que corresponde al beneficio tributario de la empresa producto de rebajar los intereses de deuda como un gasto antes de impuesto.
Con un poco de álgebra es posible mostrar que la formulación tradicional del WACC, es decir aquella en que se expresa el costo de la deuda después de impuestos kd(1 - t), en lugar de solamente kd, dado por la ecuación (1b), entrega una valoración correcta de la empresa cuando se capitalizan los flujos F = ROp (1 - t). La tabla 1 resume esta equivalencia.
La diferencia entre ambas formulaciones radica solamente en la forma en que el beneficio tributario de la deuda (kdDt) es contabilizado (ver Ross et al, cap. 17). Si este beneficio es considerado en el flujo, como en FV, entonces debe usarse WACC(*). Si este beneficio no es considerado en los flujos, es decir como en F, que es el procedimiento estándar sugerido, entonces debe usarse WACC.
Esta equivalencia entre tasas y flujos, tratada en pocos textos de finanzas, es parte fundamental de los resultados que se discutirán a continuación, ya que permite obtener tres implicancias relevantes en evaluación de proyectos. Implicancias para la evaluación de proyectos Seguidamente se reescribe la expresión general del VAN de la ecuación (1d) pero en el nuevo contexto, es decir, asumiendo flujos perpetuos y constantes, junto a los demás supuestos antes expuestos.
Debido a que por el supuesto 2 los proyectos son desarrollados por empresas en marcha, entonces los flujos de un proyecto en particular implican cambios o impactos en los flujos proyectados para la empresa como un todo. Estos impactos, atribuibles al proyecto, pueden ser denominados ΔROp(1 - t), donde Δ es el operador de diferencias, es decir, el cambio en los flujos de la empresa (flujos con y sin proyecto), o mejor aún, se les puede representar simplemente como ROp(1 - t)p, donde el subíndice P indica que se trata de los flujos específicos del proyecto.
Por el supuesto 2, las empresas desean financiar sus proyectos de una forma similar a como está financiado el resto de la empresa. Entonces, la inversión inicial total requerida por el proyecto (IT), es la suma del aporte inicial del patrimonio (IS) más el aporte de la deuda (ID). Ambos aportes son realizados en proporciones cercanas a la estructura objetivo de largo plazo de la empresa, es decir.
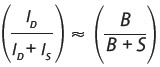
Puesto que el aporte de la deuda (ID) es el endeudamiento solicitado para financiar el proyecto, es más conveniente referirse a ella como Dp, es decir el valor libro o nominal de la nueva deuda.
Entonces, bajo los supuestos previos, la definición correcta del VAN de un proyecto viene dado ahora por los flujos operacionales esperados (atribuibles al proyecto), menos la inversión total que exige el proyecto, es decir:

donde WACC es la tasa de descuento después de impuestos de la empresa (no del proyecto), definida anteriormente en la ecuación (1b), y los flujos de fondos, ROp(1 - t), coinciden con la definición apropiada para presupuestos de capital de los libros de texto estándar (ver la fila correspondiente a la formulación estándar, con beneficio tributario de la deuda en la tasa de descuento, en la tabla 1).
El desarrollo anterior ha permitido obtener definiciones precisas de flujos y tasas basados en supuestos razonables y en un modelo formal. A partir de la redefinición del VAN de acuerdo con la ecuación (5), a continuación se obtienen tres resultados relevantes para la evaluación de proyectos, los que constituyen el punto central de esta investigación, en términos de permitir clarificar la interpretación de algunos conceptos de uso común.
Resultado 1: Independiente de cómo se haya financiado un proyecto, el VAN pertenece completamente a los propietarios del patrimonio.
Este primer resultado mostrará que la interpretación del VAN es muy precisa[7], aunque en principio contra-intuitiva. Si un proyecto es financiado con deuda y patrimonio, se tiende a pensar que el VAN que este generará se distribuirá de alguna manera entre ambas partes, pero esto no es así y puede mostrarse en el presente contexto como sigue.
El dinero aportado inicialmente por los acreedores es Id = D, y los flujos perpetuos esperados en compensación por ellos son los intereses de esta deuda dados por kdD (puesto que el carácter de deuda perpetua hace que no existan amortizaciones netas de esta deuda). La tasa de descuento de mercado apropiada para la deuda es kb. Con esto, un VAN para los acreedores es:
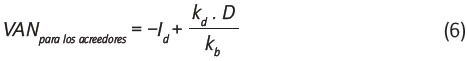
No obstante, de acuerdo con la teoría financiera clásica (Hirshleifer, 1970), el VAN de un proyecto pertenece a los propietarios del proyecto o de la idea original. La razón fundamental es que bajo el cumplimiento del supuesto 1, cualquier nuevo financiamiento es hecho a precios de mercado. La subasta competitiva por el financiamiento lleva a que la rentabilidad de la nueva fuente de financiamiento sea tal, que haga que el VAN de los nuevos acreedores o inversionistas sea cero. Este principio en realidad puede generalizarse para cualquier nuevo tipo de financiamiento, ya sea deuda, o incluso nuevas emisiones de patrimonio. Nótese que VAN=0 significa que los nuevos inversionistas reciben el rendimiento justo en función del riesgo incurrido, pero nada más que eso[8], lo cual implica que todo el VAN del proyecto permanecerá en los antiguos propietarios, un principio que puede mostrarse en el presente contexto como se muestra a continuación.
Anteriormente se señaló que
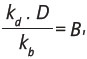
es decir, kbB = kdD, y también se señaló que el monto aportado por los acreedores (Id) es igual al valor nominal de la deuda, D. Si VANpara acreedores = 0, haciendo los remplazos anteriores en la ecuación (6) y despejando, se obtiene que Id = B, o D = B, es decir, el valor nominal de la deuda (o valor del aporte inicial al proyecto por parte de los acreedores) es igual a su valor de mercado (esto es en realidad una implicancia directa del supuesto 1).
Volviendo al VAN de la ecuación (5), el numerador puede ser reescrito ROp(1 - t) = Fs + kdD(1 - t). Adicionalmente, como por la ecuación (3) el valor del patrimonio es el valor presente del flujo de los accionistas,
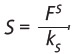
entonces FS = S kS. Remplazando esto en la ecuación (5) se tiene que:
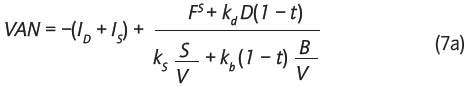
Se multiplica por 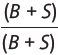 , y se obtiene
, y se obtiene
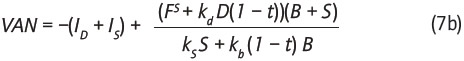
Puesto que anteriormente en la ecuación (3) se mostró que 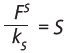 , remplazando FS = kSS en el primer término del denominador en la ecuación (7b) se obtiene:
, remplazando FS = kSS en el primer término del denominador en la ecuación (7b) se obtiene:
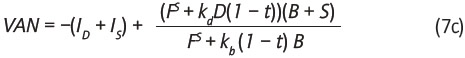
Además, como kbB = kdD, remplazando y simplificando,
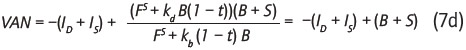
Finalmente, como Id = B, se puede concluir que el VAN de cualquier proyecto puede expresarse simplemente como:

es decir, el VAN mide la diferencia entre el valor de lo aportado inicialmente por los accionistas y el nuevo valor de mercado que tomará ese patrimonio producto de emprender el proyecto. El hecho destacable es que, como se había señalado, la deuda no obtiene nada del VAN, y este pertenece completamente a los accionistas.
Entonces la interpretación del VAN es simple: una medida del impacto esperado en la riqueza de los propietarios originales, aún cuando éste proyecto haya sido financiado con una mezcla de deuda y patrimonio. Así, el VAN tiene una interpretación única que es correcta y no contradictoria, y si existe una apropiada formulación, todos los caminos deben llevar a un mismo VAN, lo que es contrario a la visión de que este tomará distintos valores según el punto de vista que se use en la evaluación.
Resultado 2: La definición estándar del VAN obedece a una simplicidad práctica. Esta definición sugiere que tanto el costo de la deuda como el beneficio tributario de esta se reflejen en la tasa de descuento WACC, y no en los flujos
Este resultado, ya parcialmente obtenido anteriormente, se refiere al tratamiento apropiado del servicio o pago de la deuda, tanto de las amortizaciones de principal como de intereses. En la tabla 1 se comentó la equivalencia entre el VAN tradicional usando WACC, y el VAN calculado a partir del WACC(*), es decir:
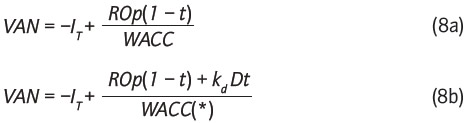
Con un poco de álgebra puede mostrarse que las expresiones en las ecuaciones (8a) y (8b) son idénticas. La implicancia de esto para presupuestos de capital es que expresiones alternativas de flujos de fondos y tasas de descuento son posibles, siempre que se pueda llegar con ellas al mismo VAN único, de acuerdo con lo anteriormente expuesto (resultado 1).
El uso de WACC(*) en lugar de WACC, obliga a calcular y explicitar el monto del servicio de la deuda para ser incluido en los flujos de cada año (ver Ilustración numérica al final del artículo). Así, es evidente que la definición o estructura ampliamente recomendada para los flujos de fondos obedece fundamentalmente a simplicidad práctica. Es más simple considerar todos estos efectos tributarios en la tasa de descuento usando kd(1 - t) en lugar de kd. Es decir, es más simple usar WACC en lugar de WACC(*).
Nótese que si la empresa paga intereses anuales por una suma igual a kdD, este costo total de la deuda puede ser descompuesto en dos partes: kdD(1 - t), que es el costo de la deuda efectivo para la empresa, o costo después de impuesto, más kdDt, que es el beneficio tributario (ahorro) para las empresas producto de usar deuda como fuente de financiamiento. Este último término es el que aparece como el segundo sumando en el numerador de (8b).
Por otro lado, nótese que en la definición estándar del VAN (ecuación 6), el costo de la deuda o intereses (kdD) no aparece rebajado en los flujos de fondos, puesto que allí se considera la utilidad operacional después de impuestos, y no la utilidad neta después de impuestos. Esto es así debido simplemente a que el costo de la deuda es incluido en la tasa de descuento WACC. Este punto es especialmente destacable, por cuanto un error común en evaluación de proyectos es incluir el servicio de la deuda (intereses y amortizaciones) en los flujos y simultáneamente usar como tasa de descuento WACC, lo que arroja una estimación sesgada del VAN. Este punto se desarrolla en el resultado 3.
En resumen, las ecuaciones (8a) y (8b) muestran que, o se considera el beneficio tributario de la deuda en la tasa de descuento, o alternativamente en los flujos de fondos, pero no en ambos simultáneamente.
Resultado 3: El VAN del proyecto es igual al VAN del inversionista, por lo que no es relevante estimar el VAN del inversionista
A partir del modelo desarrollado en este trabajo puede obtenerse un último resultado relevante, y se refiere a los diferentes tipos de enfoques de evaluación postulada por algunos autores. Sapag y Sapag (1989, p. 233) señalan que "... para evaluar un proyecto de inversión, lo lógico es medir primero la conveniencia financiera de su ejecución, el proyecto puro, y luego, la fuente de financiamiento más adecuada". En este espíritu, algunos autores postulan la existencia de una evaluación económica (proyecto puro), para analizar la rentabilidad de la inversión independientemente de la fuente de financiamiento, asumiendo que esta proviene solamente de fuentes de internas (propias) y no externas; esto, en oposición o como alternativa a una evaluación financiera o del inversionista, donde sí se consideraría el tipo de financiamiento. A continuación se muestra que, contrario a esta visión, el VAN de un proyecto tiene una sola interpretación (resultado 1), inde pendiente del punto de vista en que es medido, es decir que VAN es idéntico a VAN del inversionista.
En el contexto del modelo aquí propuesto, de acuerdo con la ecuación (2) los flujos marginales del accionista son los que quedan para ellos una vez que se han pagado todos los costos, incluidos costos financieros e impuestos, y vienen dados por FS = (ROp - kdD)(1 - t). También se señaló que la tasa de descuento apropiada para capitalizar los flujos del patrimonio, de acuerdo con la ecuación (3), es el costo del patrimonio, ks. Así, el VAN para los accionistas compara el aporte inicial de estos (IS) con el valor presente de los flujos perpetuos residuales que ellos esperan obtener, es decir:

Pero anteriormente se señaló que 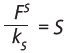 , y justamente este es un componente de la ecuación anterior, de modo que remplazando se tiene que:
, y justamente este es un componente de la ecuación anterior, de modo que remplazando se tiene que:
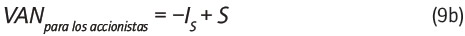
es decir, VANpara los accionistas es exactamente igual al VAN del proyecto en la ecuación (6). Luego, si se usan defini ciones consistentes de flujos y tasas, en este contexto las diferencias en ambos puntos de vista son espurias. Este resultado muestra que se puede ser indiferente en usar alternativamente una u otra definición. De aquí se deduce que una vez calculado el VAN con base en la ecuación (6), resulta un ejercicio innecesario desde el punto de vista práctico recalcular con base en la ecuación (9).
Nótese también que según la ecuación (9), el costo de la deuda (kdD) es explícitamente rebajado en los flujos, es decir, en el numerador, y por tanto no debe ser considerado nuevamente en la tasa de descuento, motivo por el cual la tasa de descuento que debe usarse en este caso es solamente la tasa del patrimonio. Con base en lo anterior, se clarifica otro error común en la evaluación de proyectos, cuando se usa la tasa de descuento WACC para actualizar los flujos residuales de los propietarios, lo que, como se muestra aquí, es un claro error.
También es relevante comentar otra forma alternativa de escribir el VAN, que se enfoca en separar flujos operacionales de los flujos financieros (ver Cap. 17, Ross et al.). Este enfoque obliga a incorporar el costo del patrimonio sin deuda, un concepto definido originalmente por Modigliani y Miller (1958), op. cit. en su proposición número 2. Sin embargo este esquema tiene un uso práctico menos común.
Por último, bien cabe preguntarse qué ocurrirá si los accionistas sistemáticamente generan un VAN positivo, en el sentido de que este VAN aumenta el valor del patrimonio, y cambia la estructura óptima de financiamiento de la empresa. Puesto que los inversionistas quieren conservar la proporción óptima de deuda, tienen dos posibilidades: entregar el VAN en la forma de dividendos extraordinarios a los accionistas, o aumentar el nivel de deuda. Cualquiera sea la decisión, es evidente que la empresa tiene mecanismos para conservar una estructura óptima, y seguir usando dicha estructura en el cálculo del WACC para fines de evaluación de proyectos.
Una ilustración numérica
A continuación se incorpora un ejemplo numérico simple para mostrar algunos de los resultados anteriores. Supóngase que una empresa tiene un patrimonio y una deuda a valores de mercado de $100 y $60, respectivamente -lo que constituye la proporción de deuda-patrimonio considerada óptima-, que la tasa de costo del patrimonio es de 20%, que la tasa de costo de la deuda es de 8%, y que los impuestos son del 30%. Con estos datos, usando la ecuación (1b), el costo del capital de la empresa es:
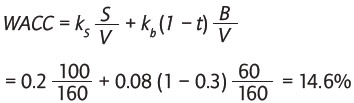
La empresa tiene un proyecto en estudio que implica un riesgo similar al riesgo de la empresa. La inversión inicial total requerida es de $16, y los flujos operacionales anuales proyectados del proyecto son de $3.34. En este caso el VAN del proyecto, usando la ecuación (6), viene dado por:
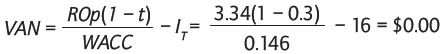
Este ejemplo muestra entonces la forma correcta (estándar) de construir los flujos y tasas de descuento para estimar el VAN.
Resultado 2: También puede mostrarse que efectivamente la definición estándar del VAN obedece a una simplicidad práctica.
Se calcula el costo del capital de la empresa antes de impuestos:
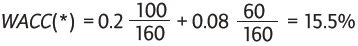
En este caso, de acuerdo con la equivalencia de las ecuaciones (8a) y (8b), el VAN del proyecto viene dado por:
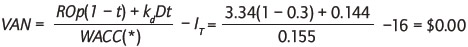
Luego, puede llegarse al VAN de otro modo, como en este caso, pero requiriendo cálculos adicionales innecesarios, en particular estimar los intereses de la deuda en los flujos del numerador.
Resultado 3: Finalmente, se muestra que el VAN del proyecto es igual al VAN del inversionista.
Usando la ecuación (9) se obtiene el VAN desde el punto de vista del inversionista, observando que, con base en la estructura de capital objetivo, el aporte de estos debe ser de $10, y el aporte de los acreedores de $6:
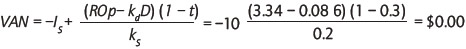
Puesto que ambos resultados son idénticos, queda ilustrado numéricamente que el punto de vista en la evaluación de proyectos es irrelevante.
Una extensión numérica al caso no perpetuo
Resultados similares, aunque más aproximados, pueden obtenerse para el caso no perpetuo, es decir, levantando uno de los supuestos del modelo. Para esto se asume que la empresa en estudio está considerando un proyecto con la misma inversión, pero que el proyecto tiene una vida de solamente tres años, y que los flujos operacionales proyectados son de $9.945 por año. En este caso, el VAN del proyecto es:
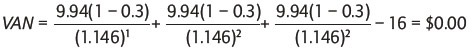
usando como tasa de descuento el WACC, ya que sus componentes, incluyendo la estructura de capital objetivo, no han cambiado.
En el caso del punto de vista del inversionista, se construye la tabla de pago de la deuda como sigue:
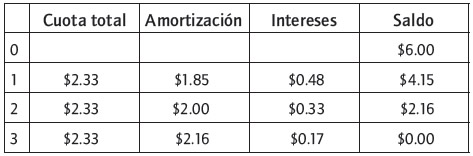
Usando la ecuación (9), el VAN para el inversionista es:
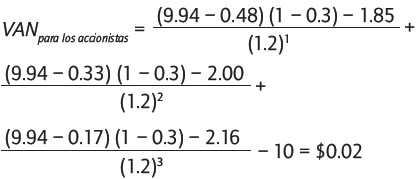
En este caso, el resultado obtenido es solo aproximado, aunque muy cercano, debido al levantamiento de uno de los supuestos originales.
En la enseñanza de la evaluación de proyectos en Latinoamérica, tanto a nivel de pregrado como de posgrado o cursos de especialización de proyectos, puede apreciarse la necesidad de definir con mayor precisión conceptos básicos tales como la misma interpretación del valor actual neto, y lo que se ha venido entendiendo como punto de vista del proyecto puro o punto de vista del inversionista. También se ha postulado la existencia de evaluaciones sin financiamiento y con financiamiento.
Aparentemente, los problemas han surgido debido a que algunos conceptos clave de la evaluación de proyectos no siempre han sido tratados con la necesaria claridad. Por esto, a través de la definición de solo tres supuestos básicos y un marco de análisis preciso como el de Modigliani y Miller, en este estudio se demuestra que en realidad el origen de las distinciones o puntos de vista señalados anteriormente no tienen fundamento. En efecto, la definición del VAN es algo muy preciso, dejando poco espacio para confusiones.
Un primer resultado muestra que el VAN tiene un significado muy preciso, esto es, el cambio esperado en la riqueza de los propietarios o accionistas, atribuible a la implementación del proyecto. Dicho de otro modo, es el cambio esperado en el valor de mercado del patrimonio o capital propio. Este significado tan exacto del VAN prácticamente no deja espacio para interpretaciones alternativas.
Un segundo resultado ha sido mostrar que definiciones alternativas de la tasa de costo del capital, ya sea antes de impuestos (WACC(*)) o el tradicional WACC expresado después de impuestos, si se usan los flujos de fondos apropiados en cada caso, entonces el VAN no cambia. De aquí surge la importancia de destacar la coherencia que debe existir entre flujos y tasas, algo que en la práctica no siempre ha sido analizado con la precisión requerida. En efecto, al momento de estimar la tasa de descuento, se dice por ejemplo que esta debe ser digamos 15% real. Sin embargo, muy pocas veces existe la claridad como para indicar si esta tasa se refiere al costo promedio del capital o solo a la tasa de descuento apropiada para los accionistas.
Un último resultado ha mostrado que el punto de vista en la evaluación de proyectos no es relevante. En efecto, un proyecto evaluado desde el punto de vista del inversionista, o evaluado desde el punto de vista del proyecto como un todo, arroja idénticos resultados en el marco de Modigliani y Miller. Además, la equivalencia de estos resultados es mostrada bastante bien aproximada cuando se trata de flujos finitos.
En resumen, el principal resultado del trabajo es probar que si bien es posible llegar a resultados similares usando procedimientos alternativos, la práctica comúnmente aceptada al evaluar proyectos (es decir, las convenciones propuestas por los libros de texto), donde se considera la inversión total (independiente de su origen), los flujos operacionales esperados sin deuda, y la tasa de costo promedio del capital después de impuestos, son en conjunto, acertadas. Finalmente, aunque es posible plantear esquemas alternativos también consistentes, en la práctica parece ser innecesario, y en algún caso injustificable, puesto que en definitiva conducen al mismo resultado final.
[1] Los autores agradecen el apoyo financiero del Núcleo de la Iniciativa Científica Milenio "Ciencia Regional y Políticas Públicas" (Mideplan, Chile).
[2] En Latinoamérica la traducción de la palabra capital es generalmente ambigua. Sin embargo, en finanzas, capital se refiere a todas las fuentes de financiamiento, que incluyen patrimonio (equity o stock shares) y deuda (debt).
[3] Hamada (1969) muestra que el CAPM y la teoría de la estructura de capital de Modigliani y Miller son consistentes entre sí.
[4] Respecto a la precisión de los supuestos de una teoría, la mayoría de los economistas actualmente comparten la visión de Friedman (1953), en el sentido de que lo realmente importante es la capacidad de la teoría para explicar y predecir los fenómenos.
[5] Miles y Ezzell (1980) desarrollan una aplicación con flujos finitos.
[6] En realidad puede plantearse que el flujo total de la empresa se reparte entre tres, si se toman en cuenta los impuestos reclamados por el Gobierno. Pero esto puede simplificarse a solo dos, si estos reclamos son considerados después de impuestos.
[7] Nótese que existe una diferencia clave entre la precisión con la que se puede definir un determinado concepto (en este caso, el VAN) y la precisión con la que ese concepto puede ser medido o estimado en la realidad. Por ejemplo, el operador de la esperanza matemática está claramente definido (y el VAN es de hecho una esperanza); sin embargo, solo en casos muy especiales puede ser estimada con certeza.
[8] Si por algún motivo el VAN de los nuevos acreedores fuera positivo, la empresa podría seguir esperando hasta que aparezcan nuevos inversionistas dispuestos a obtener menores rentabilidades (un menor VAN). La empresa solo debe finalizar la subasta cuando aparezca un acreedor dispuesto a obtener un VAN=0.
Black, F. (1972). Capital Market Equilibrium with Restricted Borro wing. The Journal of Business, 45(3), 444-455. [ Links ]
Brealey, R. & Myers, S. (1998). Principios de finanzas corporativas (4a. ed.). España: McGraw-Hill. [ Links ]
Copeland, T. & Weston, J. (1988). Financial Theory and Corporate Policy (3rd. ed.). Boston: Addison Wesley Pub. Co. [ Links ]
Emery, D. R. & Finnerty, J. D. (2000). Administración financiera corporativa (5a. ed.). México D.F.: McGraw-Hill. [ Links ]
Fontaine, E. R. (1999). Evaluación social de proyectos (12a. ed.). México: Alfaomega Grupo Editor, Ediciones Universidad Católica de Chile. [ Links ]
Friedman, M. (1953). Essays in Positive Economics. Chigago, IL: Chicago Press. [ Links ]
Graham, J. R. & Harvey, C. R. (2001). The theory and practice of corporate finance: evidence from the field. Journal of Financial Economics, 60, 187-243. [ Links ]
Hamada, R. S. (March, 1969). Portfolio Analysis, Market Equilibrium and Corporation Finance. The Journal of Finance, 24(1), 13-31. [ Links ]
Hamada, R. S. (May, 1972). The Effect of the Firm's Capital Structure on the Systematic Risk of Common Stocks. The Journal of Finance, 27(2), 435. [ Links ]
Harris, M. & Raviv, A. (1991). The theory of capital structure. The Journal of Finance, 46, 297-356. [ Links ]
Hirshleifer, J. (1970). Investment, Interest and Capital. Engle wood Cliffs, N.J.: Prentice-Hall. [ Links ]
MacKay, P. & Phillips, G .M. (2005). How does industry affect firm financial structure? Review of Financial Studies, 18(4), 1433-1466. [ Links ]
Miles, J. & Ezzel, J. (1980). The Weighted Average Cost of Capital, Perfect Capital Markets, and Project Life: A clarification. Journal of Financial and Quantitative Analysis, 15, 719-730. [ Links ]
Modigliani, F. & Miller, M. (1958). The Cost of Capital, Corporation Finance and the Theory of Investment. American Economic Review, 48(3), 261-297. [ Links ]
Modigliani, F. & Miller, M. (1963). Taxes and the Cost of Capital: A Correction. American Economic Review, 53(3), 433-443. [ Links ]
Ross, S. A., Westerfield, R. W. & Jaffe, J. F. (1999). Finanzas corporativas (5a. ed.). México D.F.: McGraw-Hill. [ Links ]
Sapag, N. & Sapag, R. (1989). Preparación y evaluación de proyectos (2a. ed.). Bogotá: McGraw-Hill. [ Links ]
Sapag, N. & Sapag, R. (2000). Preparación y evaluación de proyectos (4a. ed.). Bogotá: McGraw-Hill Interamericana. [ Links ]
Sharpe, W. (1974). Capital Assets Prices: A Theory of Market Equili brium under Conditions of Risk. Journal of Finance, 19(3), 425-442.













