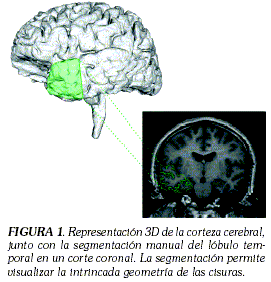
^a Grupo de Investigación BioIngenium, Centro de Telemedicina, Universidad Nacional de Colombia, Bogotá, D.C.

* Correspondencia: adruedao@unal.edu.co. Dirección postal: Centro de Telemedicina, Universidad Nacional Ciudad Universitaria, Bogotá,D.C.

En este trabajo presentan de manera didáctica los modelos más usados para deformar superficies tridimensionales y su aplicabilidad en la morfometría de estructuras anatómicas, a partir de pilas de imágenes médicas. Estos modelos permiten simplificar una geometría compleja por medio de alguna manipulación matemática de la superficie, con el objetivo de facilitar la realización de estudios de anatomía comparativa en órganos complejos y sobre grandes volúmenes de población.

Palabras clave: morfometría, mapeo de superficies, alisado de superficies.

Abstract

Key words: morphometry, surface mapping, surface smoothing.

Introducción

La visualización y análisis de las características funcionales y anatómicas de algunas estructuras se puede facilitar mediante modelos tridimensionales obtenidos por segmentación, a partir de imágenes de tomografía computarizada (CT, Computer Tomography) o resonancia magnética (MR, Magnetic Resonance). La determinación de longitudes y áreas en estas superficies se dificulta debido a la intrincada geometría de algunas estructuras anatómicas, como la corteza cerebral, órganos huecos como el colon, etc. En el caso de la corteza cerebral, la compleja e intrincada forma de algunas circunvoluciones y cisuras no permite calcular de manera exacta el valor de las áreas funcionales, tal como se muestra en la Figura 1. Sin embargo, algunas de estas aplicaciones morfométricas se pueden simplificar si las mediciones se realizan sobre otra superficie más suave, con una topología similar y que conserve las métricas lo más posible.

Por otro lado, las deformaciones de superficies tridimensionales y sus aplicaciones han sido tema de estudio en los últimos veinte años. Los modelos deformables se aplican actualmente en diferentes áreas, para automatizar procesos como segmentación, registro, medición, ajuste y otros relativos a imágenes médicas.

Básicamente, se denominan modelos deformables a aquellos en los que un contorno bidimensional, o una superficie tridimensional, se hacen evolucionar hasta que toman la forma de otro contorno, o superficie objetivo. De acuerdo con lo presentado por Montagnat et al. [1] en su revisión, los campos de acción en los cuales se aplican los modelos deformables cubre el reconocimiento de patrones, animación computarizada, simulación de cirugías y la segmentación de imágenes, entre otras. También se utilizan diferentes representaciones para generar desde líneas 3D deformables hasta volúmenes deformables. Los modelos deformables fueron introducidos por Kass et al. [2] en 2D, y extendidos al caso 3D por Terzopoulos et al. [3]. Algunos de los modelos deformables reseñados por Montagnat et al., como level sets, spring-mass y modelos de elementos finitos también se incluyen aquí, junto con algunas otras aproximaciones relacionadas y combinaciones de éstas.

Este trabajo pretende proporcionar una introducción a los modelos potencialmente útiles para deformar superficies, que faciliten mediciones en órganos complejos a partir de información 3D de las imágenes médicas. Para ello, se plantea en primera instancia una breve descripción del problema, para luego introducir al lector en los modelos para deformar superficies, junto con una clasificación somera de los modelos que se verán más adelante. A continuación se hace un recuento de los métodos para aplanar superficies, se reseñan los modelos de suavizado de superficies, se describen los modelos para mapear superficies y se presentan algunos de los métodos para realizar metamorfosis entre superficies. Finalmente, esta información se complementa con algunas de las aplicaciones de los modelos de deformación de superficies, en especial, la morfometría basada en superficies.

Definición del problema

En los últimos años, la medicina ha sido invadida por avances tecnológicos que han modificado de muchas maneras el ejercicio profesional. Los recursos computacionales en particular, se han convertido en una importante herramienta en toma de decisiones más acertadas acerca de la condición del paciente y de su tratamiento. Algunos tipos de imágenes médicas permiten obtener representaciones bidimensionales y tridimensionales (conjuntos de voxeles¹ , mallas poligonales, etc.) de las estructuras anatómicas del paciente, de tal manera que el médico las puede estudiar con más comodidad y precisión. Diversos paquetes de software desarrollados en la actualidad, permiten simular por ejemplo, los efectos a largo plazo de un tratamiento o de una cirugía. Muchas herramientas proporcionan medidas más precisas y son mucho más rápidas para efectuar análisis complejos.

La morfometría o biometría, es decir, el estudio cuantitativo de las estructuras anatómicas, es un elemento potencialmente importante en el diagnóstico, el pronóstico y el seguimiento de la condición de un paciente. Las mediciones sobre algún órgano, cuando se realizan, generalmente se hacen de forma manual, siendo vulnerables a errores en la medición y, como consecuencia, producen pérdida en la precisión y confiabilidad de la medida [4].

Existen paquetes de software que permiten realizar mediciones exactas sobre superficies lisas y sencillas; sin embargo, este tipo de mediciones es muy difícil en superficies más complejas e intrincadas, pues es necesario considerar factores tales como el cambio en los ángulos, en las curvaturas, los cambios topológicos, las relaciones locales y globales de la superficie, etc., que determinan la precisión en las mediciones. Para resolver este problema, una aproximación posible consiste en deformar la superficie inicial para simplificar la geometría, con lo cual se pueden aplicar entonces, algoritmos de medición para superficies sencillas. El proceso de deformación de estas superficies se puede hacer de diferentes maneras, tal como se explicará mas adelante. Un elemento adicional que se considera, es la posibilidad de transformar una superficie en otra, con el objetivo de comparar las mediciones realizadas en cada una de ellas.

Algunos de los términos relativos a la deformación de superficies y que se encontrarán más adelante son:

* Mapeo conforme (conformal map): se refiere a una función que preserva ángulos; las formas pequeñas se conservan y las áreas, sólo de forma aproximada.

* Distancia geodésica: se define como la ruta más corta entre dos puntos en un espacio con una métrica definida.

* Curvatura: es básicamente la cantidad que mide la desviación de un objeto geométrico con respecto a un plano. En superficies, se encuentran las curvaturas principales, k₁ y k₂, que indican la curvatura mínima y máxima en un punto de la superficie; la curvatura media, que es el promedio de las curvaturas principales y la curvatura Gaussiana, que es el producto de k₁ y _k2.

Modelos para deformar superficies

Los modelos para deformar superficies, reseñados en la literatura más reciente se pueden clasificar en cuatro grandes grupos como lo muestra la Figura 2. Los modelos que aplanan una superficie buscan obtener una representación en el plano euclidiano de la superficie 3D, insertando, si es necesario, líneas de corte que mejoren la proyección. Con los modelos que suavizan la geometría de la superficie se obtiene una representación alisada que conserva la forma básica, pero elimina los picos y valles demasiados pronunciados. Con la aplicación de los métodos de mapeo de superficies se busca proyectar los puntos de la superficie 3D en otra de geometría más simple (como una esfera). Por último, con los métodos de metamorfosis entre superficies se busca la transformación que permite deformar una superficie en otra y las superficies correspondientes, a los pasos intermedios de la transformación.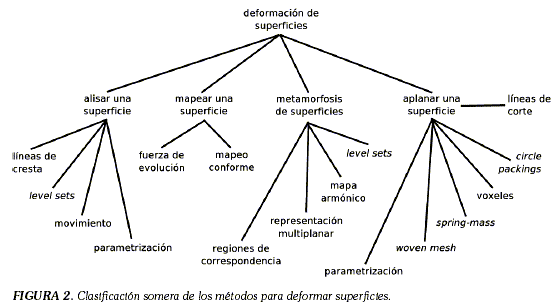

A. Aplanar una superficie

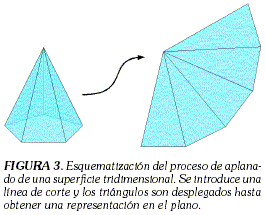
Este es el primer problema que se consideró en deformación de superficies, dada su similaridad con el problema de elaborar mapas, cuyo objetivo es el de obtener representaciones planas de una superficie curvada. La cantidad de puntos de la superficie original se conserva en la representación en el plano, pero las distancias, ángulos y áreas, se afectan significativamente entre más compleja y curva sea la superficie. En esas situaciones se utilizan las líneas de corte, que ayudan a corregir un poco la distorsión en las métricas. En la Figura 3 se presenta el resultado obtenido al aplicar un método para aplanar la superficie. En este caso particular, es necesario insertar una línea de corte en la superficie para lograr una representación plana de la superficie inicial.

La solución al problema de elaborar mapas [17] puede considerarse una aproximación muy primitiva pero válida por ser la pionera. Básicamente, se presentan los lineamientos de un algoritmo que permite alisar superficies no convexas, el cual se basa en calcular una matriz con las distancias entre los puntos de la superficie curva; luego, se determina un conjunto de puntos en el plano cuya matriz de distancias se ajuste a la calculada para la superficie inicial, usando el método del descenso del gradiente de Newton-Raphson y el algoritmo para calcular las distancias mínimas, presentado por Wolfson et al. [18]. Junto con otros ajustes (como la cantidad de vecinos que se evalúan), la representación plana obtenida representa adecuadamente la forma alisada de la superficie original.

Más recientemente se han presentado diferentes aproximaciones, que resuelven de la forma más exacta posible el problema de aplanar una superficie:

Parametrización: Floater [19] presenta el desarrollo matemático necesario para elaborar una parametrización para una superficie de triangulación, de forma que la imagen obtenida sea una representación plana de esta superficie. Básicamente se hace una consideración sobre los vecinos en cada punto y se desarrollan tres diferentes parametrizaciones: uniforme, mínimos cuadrados ponderados y preservación de la forma, las cuales son comparadas al final para determinar la mejor aproximación.

Circle Packings (empaquetar círculos): Este método fue presentado inicialmente por Hurdal et al. [20] y retomado y redefinido posteriormente [21] por los mismos autores. Aunque se trata de un método que no preserva totalmente las métricas, se considera una aproximación discreta que permite generar representaciones planas de la superficie en el plano euclidiano y en el plano hiperbólico. Se trabaja sobre una malla de triangulación, se colocan círculos con centro en cada vértice de la malla y el radio del círculo se va ajustando de acuerdo a una condición sobre la suma de los ángulos que se pueden construir en cada vértice. También se elaboró un paquete de software, CirclePack, que implementa este método.

Basada en voxeles: Dado que la representación general de las superficies 3D está basada en voxeles, Grossmann et al. [22] desarrollaron un método directo que opera sobre los voxeles de la superficie, el cual requiere de dos pasos: el cálculo de las distancias geodésicas mínimas entre los voxeles y la búsqueda de una configuración de puntos en 2D, cuyas distancias euclidianas aproximen lo más posible las distancias geodésicas entre los voxeles. El método es rápido, pues no requiere del cálculo de una superficie de triangulación y conserva de forma aproximada las métricas globales.

Spring-Mass: Presentado por Wang et al. [23], éste método se enfoca en la aplicación de un modelo spring-mass (masas y conexiones), que se rige principalmente por la minimización de una función de energía y por términos que indican la precisión en la forma y en el área. Es relativamente rápido y generalmente requiere de pocas iteraciones para obtener buenos resultados. El modelo spring-mass es retomado y modificado por Li et al. [24], incluyendo, además de las conexiones de tensión del modelo original, conexiones cruzadas que minimizan la distorsión de la representación resultante. La superficie se divide en cintas de triángulos que se van aplanando una a una, y para eliminar las posibles superposiciones de triángulos, se considera la energía global de relajación, un procedimiento local de corrección y algunas restricciones en la evolución.

Woven mesh: Es el método más reciente, presentado por Wang et al. [25] y se basa en la construcción de una malla entrecruzada (woven mesh), utilizando dos tipos de mapeo: el de nodos de tensión, que va adicionando los nodos sobre dos rutas perpendiculares en la superficie y el mapeo diagonal de nodos, que agrega los nodos ubicados en los cuadrantes. Luego se minimiza una función de energía que mide las deformaciones de longitud y área entre los nodos en la superficie y los nodos en la representación planar, lo que permite establecer una parametrización entre todos los puntos de cada una de las superficies.

Un elemento adicional que se considera en los modelos para aplanar una superficie 3D, es el de líneas de corte en una superficie con complejidad geométrica alta, para garantizar que la representación plana corresponderá de mejor forma con la superficie inicial. En algunas aproximaciones iniciales, estas líneas de corte las podía estimar el usuario de forma manual. Más recientemente, Wang et al. [26] presentan un método para automatizar esta labor, el cual evalúa, en cada punto de la malla de triangulación, la curvatura Gaussiana y la utiliza como criterio para establecer la cantidad y longitud de las líneas de corte que se deben aplicar a la superficie. El proceso de aplanado se realiza por medio de un modelo spring-mass modificado.

B. Alisar una superficie

El proceso de suavizado puede generar una superficie con menos puntos, con lo cual se reduce el espacio en disco que ocupa la representación y el tiempo de procesamiento de la misma. En la Figura 4 se presenta el resultado de alisar una representación 3D del tallo cerebral.

Algunas de las aproximaciones más relevantes en este campo se presentan a continuación:

Parametrizaciones: Un método de suavizado, utilizando parametrizaciones relacionadas con multirresolución de mallas es presentado por Lee et al. [27]. La idea básica es simplificar la malla de triangulación de forma iterativa utilizando mapas conformes, de forma que se establezca una jerarquía y luego, cada punto de la malla inicial, se asocia con cada una de las diferentes resoluciones. Es una solución rápida y no restringe la topología de la malla.

Sheffer et al. [28] se concentran en una parametrización que únicamente tiene en cuenta la preservación de los ángulos. Su argumento es que para preservar las características métricas, únicamente se necesita que se mantenga el valor de los ángulos en cada iteración de la evolución de la superficie. Plantean un problema de minimización en término de los ángulos, con restricciones que se van modificando si se observa que se generan intersecciones en la frontera. También puede aplicarse para generar múltiples resoluciones de la malla inicial.

Un tercer ejemplo de parametrización es introducido por Khodakovsky et al. [29]. El proceso se basa en dividir la superficie en regiones triangulares y luego, para cada una de éstas, calcular el mapeo en el dominio de parámetros, cuya base es generada con la simplificación de la malla original por eliminación de vértices. El proceso considera la calidad de los triángulos y la distorsión métrica.

Level sets: Hermosillo et al. [30] presentan una aproximación al problema de suavizado empleando level sets. Se consideran las características que gobiernan el movimiento de la superficie de acuerdo a su curvatura media, en los casos de la preservación del área y la preservación del volumen, las cuales se integran a la formulación de level sets que aproxima estos movimientos. Adicionalmente, se determinan las condiciones que permiten mantener la correspondencia entre los puntos a lo largo de la evolución de la superficie.

La combinación de los modelos de level sets y la técnica de difusión anisotrópica para el suavizado de superficies es presentado por Tasdizen et al. [31]. Se utilizan level sets con flujos de cuarto nivel, uno de los cuales es la difusión anisotrópica, representados con ecuaciones diferenciales parciales. El proceso consiste en resolver la difusión anisotrópica en el mapa normal de la superficie y luego la superficie se deforma aplicando los level sets, hasta que se ajusta a las normales suavizadas. Se aplican conceptos de minimización del mapa normal de energía y reajuste de la superficie.

Estimación de la velocidad: Pons et al. se enfocaron en la preservación del área al suavizar una superficie [32]. Su enfoque se basa en tomar un movimiento normal dado por el usuario y que generalmente se basa en la curvatura media y construir, a partir de él, una velocidad tangencial apropiada que preserve el área, a medida que evoluciona la superficie. El método puede aplicarse en superficies de triangulación y en level sets, pero únicamente se presentan resultados con la implementación en level sets.

Líneas de cresta: Stylianou et al. [33] presentan la utilización de líneas de cresta para suavizar una superficie. El objetivo de establecer las líneas de cresta es que permiten particionar la superficie creando un diagrama geodésico de Voronoi, con el cual se puede implementar un algoritmo rápido de alisar superficies, el cual combina el mapeo baricéntrico de Tutte y las coordenadas de valor medio de Floater. Las líneas de cresta se calculan de acuerdo a una aproximación de la curvatura y a una esqueletización. La distorsión métrica introducida por este método parece ser mínima.

C. Mapear una superficie

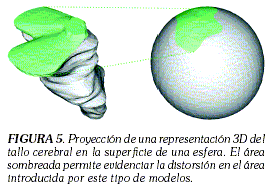
Los métodos que permiten mapear una superficie 3D, en otra con las mismas características topológicas, utilizan generalmente una esfera, o un elipsoide como superficie objetivo. El que este método pueda utilizarse se justifica con la aplicación de la geometría de superficies de Riemann, con la que se puede afirmar que cualquier superficie sin hoyos, o intersecciones consigo misma, se puede mapear de forma conforme en una esfera y cualquier porción de la superficie se puede mapear en un disco [34]. En la Figura 5 se presenta el resultado que se obtiene al aplicar un método para mapear una superficie 3D, como el tallo cerebral, en otra superficie suave, en este caso una esfera.

El objetivo principal de estos métodos es determinar un mapa conforme entre la superficie y la esfera, pero varían las formas de llegar a este mapeo. Se pueden encontrar métodos que aplican elementos finitos para construir el mapa conforme, como el presentado por Haker et al. [34], que adicionalmente considera la aplicación de texturas y la generación de mapas de coordenadas. En la misma línea, Angenent et al. [35] presentan la aplicación del operador de Laplace-Beltrami que, junto con la formulación por elementos finitos, permite construir el mapa conforme y mapear así la superficie en una esfera. Otra forma de construir un mapa conforme esférico es la presentada por Ju et al. [36], en donde se utiliza el mapeo conforme por mínimos cuadrados introducido por Levy et al. [37], el cual no preserva muy bien las métricas, pero invierte menos tiempo en los cálculos. Uno de los métodos más recientes para construir un mapa conforme único entre una superficie y una esfera es presentado por Wang et al. [38], en donde se aplican los elementos de la geometría diferencial para construir un homeomorfismo entre las superficies y luego éste se deforma de forma que minimice la energía armónica.

Otra forma de obtener una representación esférica de una superficie 3D, que es un poco más sencilla de formular, pero que no ofrece tan buenos resultados de forma directa, es plantear una fuerza que mueva cada uno de los puntos de la superficie inicial hacia la superficie de la esfera. Fischl et al. [16] presentan un método con esta característica y consideran, para cada punto y en cada iteración, una fuerza de suavizado y una fuerza radial. El método requiere de un paso posterior para uniformizar la densidad de puntos en la esfera.

D. Metamorfosis de superficies

A primera vista se podría pensar que la metamorfosis de superficies tiene muy poco en común con los demás métodos; sin embargo, podría funcionar de forma similar al método de mapeo en superficies más sencillas, tomando la superficie 3D inicial y la esfera o elipsoide (o alguna otra superficie suave) como la superficie objetivo. Una de las características de los demás métodos, que no tienen los modelos de metamorfosis de superficies, es la preservación de métricas, ya que no se aplican restricciones sobre la superficie inicial y la superficie objetivo. En la Figura 6 se presenta el resultado esperado al realizar la metamorfosis entre dos superficies.

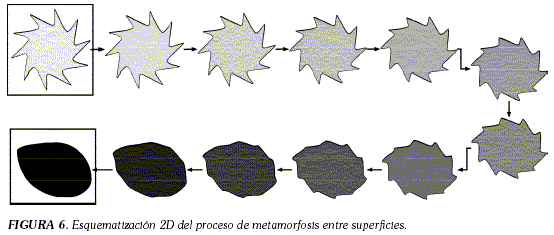
Los métodos de metamorfosis entre superficies requieren, en la mayoría de los casos, la intervención del usuario para establecer algunos parámetros, o elementos básicos necesarios para el proceso, de tal forma que son más propensos a errores; sólo unos pocos son completamente automáticos.

A continuación se destacan algunos desarrollos recientes en esta área:

* Kanai et al. [39] presentan una transformación rápida entre superficies 2D o 3D, basada en la construcción de un mapa armónico entre las superficies y un disco unitario, que sirve para establecer la correspondencia uno-a-uno entre los puntos de las superficies. Se requiere de la intervención del usuario para definir una marca de posición en cada una de las superficies.

* Un elemento novedoso, denominado representación multiplanar, es introducido por Ramasubramanian et al.[40] y aplicado a la transformación entre superficies. La representación multiplanar toma una superficie 3D y construye un conjunto de planos 2D que la representan totalmente, con lo que es posible aplicar algoritmos de metamorfosis 2D. En cada plano se almacena un conjunto de superficies, determinadas por una parametrización basada en radios. Se requiere que el usuario defina un eje, que afecta la cantidad de planos y la forma de las superficies y algunas correspondencias entre los planos, en caso de que no puedan ser determinadas por el algoritmo.

* Zockler et al. [41] presentan un método de metamorfosis basado en regiones de correspondencia y puntos de ajuste, los cuales deben ser identificados completamente por el usuario en la etapa inicial. El algoritmo se encarga de establecer una parametrización entre cada par de regiones, de ajustarlas de acuerdo a los puntos puestos por el usuario y de generar las superficies intermedias de la transformación, de acuerdo a una interpolación.

* Una aplicación del modelo de level sets 3D es presentada por Breen et al. [42]. Se construye un level set que se ajusta a la superficie inicial y se deforma, de manera progresiva, de acuerdo a la optimización de una función objetivo que actúa como medida de similaridad entre los objetos, hasta que alcanza la forma de la superficie final. Este método es completamente automático, pero no puede ser utilizado con superficies abiertas.

* Finalmente Treece et al. [43] presentan la extensión de un método de transformación 2D a la metamorfosis de superficies 3D, para lo cual utilizan volúmenes de distancias, representaciones en esferas y vectores de correspondencia entre esferas. Es un procedimiento algo complejo que requiere de la intervención del usuario en cada etapa, para determinar ciertos parámetros.

Aplicaciones

La primera aplicación de los modelos de deformación de superficies fue elaborar un mapa a partir de una superficie curva, como lo es el globo terráqueo. En la actualidad, las aplicaciones de estos métodos abarcan campos muy variados, desde el diseño de prendas de vestir, hasta la recreación de animaciones 3D; pero estando centradas la mayoría de ellas, en el campo de la medicina.

El diseño de prendas de vestir y de zapatos es una de las aplicaciones más directas de los métodos para aplanar superficies [23, 25, 44]. Se utiliza una representación tridimensional del cuerpo de la persona y sobre ella se determina la superficie que cubrirá la prenda; luego ésta es extraída y aplanada, insertando las líneas de corte necesarias. Este modelo plano se imprime, para luego cortar las telas y fabricar las prendas que se ajustan perfectamente al cuerpo de la persona. El diseño de zapatos se realiza con un procedimiento similar.

Otro grupo de aplicaciones se relacionan directamente con el procesamiento de gráficas. Los métodos de metamorfosis entre superficies pueden utilizarse para elaborar algunas animaciones y efectos especiales en las transiciones, de mucha aplicación en el cine, la televisión, la publicidad y el diseño gráfico. De igual forma los métodos para suavizar superficies permiten obtener múltiples resoluciones de una malla poligonal, facilitando el manejo de estas estructuras en tareas tales como almacenamiento, visualización, edición y transmisión. La adaptación de mapas de texturas a una superficie se puede conseguir utilizando los métodos de aplanado y de mapeo de superficies [45].

Pero como ya se mencionó, el campo de la medicina es en el que se concentran la mayor parte de las aplicaciones de los modelos de deformación de superficies. Basándose en estos métodos, se construyen paquetes de software que permiten a los profesionales de la salud analizar de una manera más precisa y segura las estructuras anatómicas de sus pacientes, así como establecer comparaciones entre ellas. Utilizando los métodos para aplanar superficies se pueden analizar vasos sanguíneos, con el fin de detectar y visualizar patologías como estenosis y pólipos, aplicación presentada por Zhu et al. [46]; así como el interior del estómago, de acuerdo a lo presentado por Mori et al. [47].

Dentro de la medicina, el área con mayor número de publicaciones sobre deformación de superficies es la relativa a las estructuras cerebrales, puesto que la corteza cerebral es considerada la superficie más compleja del cuerpo humano, en cuanto a geometría y a topología se refiere. La aplicación de estos métodos permite la identificación de cambios en los surcos del cerebro debidos a tumores u otras patologías y también facilita la visualización de las diferentes áreas funcionales del cerebro, así como la determinación de distancias y otras medidas.

Morfometría basada en superficies

Una vez obtenida una representación simplificada de una superficie 3D, es importante revisar los análisis que pueden aplicarse sobre esta nueva superficie. En la medicina, una de las aplicaciones más comunes son los estudios morfométricos, es decir, la toma de medidas con el objeto de compararlas con las de otros sujetos, o con un atlas, o para observar los cambios producidos durante la evolución de la estructura anatómica. Estas mediciones permiten la detección de tumores y otras enfermedades que afecten la forma de las estructuras anatómicas.

De acuerdo con la investigación en morfometría realizada por Ashburner [48], existen tres métodos morfométricos principales: la morfometría basada en deformaciones, la morfometría basada en tensores y la morfometría basada en voxeles. Cada método identifica elementos diferentes (diferencias anatómicas macroscópicas, diferencias estructurales en regiones y composición local, respectivamente), se aplican exclusivamente al cerebro y son utilizados para comparación entre pacientes.

Las medidas morfométricas básicas que se pueden tomar sobre la superficie incluyen longitudes o distancias, áreas, ángulos, curvaturas, grosor, etc. Es necesario resaltar que la característica más importante que deben poseer los métodos de deformación de superficies es que la nueva representación simplificada preserve la mayoría de las métricas de la superficie 3D original, pues de otra forma no tendría gran aplicación. La superficie puede estar representada por una malla de triangulación, por voxeles, o por alguna otra estructura y los métodos de medición son dependientes del tipo de estructura que se utilice.

Entre los desarrollos relacionados con este campo se encuentra la estimación de áreas basada en voséeles y presentada por Windreich et al. [49]. El método requiere dos pasos: detectar y delimitar la región de interés, para luego estimar el área de la región. El usuario debe indicar algunos puntos que indican la región de interés, los cuales son conectados, de acuerdo a la ruta más corta para delimitar la región. Luego, se aplica el estimador de área de Mullikin & Verbeek para aproximar el área de la región. Nótese que el estimar la ruta más corta entre cada par de puntos permite calcular distancias entre éstos, pudiéndose obtener el perímetro de la región de interés.

Otro trabajo relacionado es el presentado por Chung et al. [50]. En éste se presenta una aproximación estadística para realizar morfometría basada en superficies de la corteza cerebral. El cálculo de las medidas consideradas en este trabajo está basado en el tensor métrico de Riemann, el cual permite medir longitudes, áreas y ángulos y cuyo diferencial permite estimar cambios en el área y en la curvatura de la superficie. Esta aproximación no requiere la definición de una región de interés.

Conclusiones

Los métodos para deformar superficies constituyen una herramienta muy valiosa al momento de simplificar análisis y procesamientos en diferentes disciplinas, como la computación gráfica, el diseño gráfico y de modas, entre otras. El área en la que se han aplicado la mayoría de modelos de deformación de superficies es la medicina, en donde se facilita la visualización de las características estructurales y funcionales de los volúmenes anatómicos, construidos a partir de pilas de imágenes médicas. Los análisis que se pueden realizar sobre estas superficies son más precisos y proveen información adicional sobre la condición del paciente.

Existen diferentes clases de deformaciones de superficies: aplanado, alisado, mapeo y metamorfosis, bajo las cuales se pueden agrupar los métodos publicados más recientemente. Las características particulares de cada método lo pueden hacer más o menos adecuado para ciertos tipos de problemas, pero gracias a la diversidad de modelos planteados, es posible encontrar alguno con el que se obtengan resultados satisfactorios.

Enfocándose en el problema particular de morfometría de estructuras anatómicas, se concluye que el grupo de métodos menos aplicable es el de metamorfosis de superficies, ya que no garantiza la preservación de métricas, la cual es una condición necesaria para asegurar la precisión en los análisis morfométricos. Trabajos futuros en esta área incluyen determinar si la combinación de dos o más de estos métodos influye positivamente en la preservación de métricas, desarrollar métodos que se adapten a la complejidad de pequeñas áreas de la superficie y estudiar la aplicabilidad de un modelo basado en el centro de masa y los vectores normales, entre otros.

¹ Volume elements. Los voxeles de una representación 3D son equivalentes a los pixeles de una imagen 2D. Volver

Referencias

1. Montagnat J, Delingette H, Ayache N. A review of deformable surfaces: topology, geometry and deformation, Image and Vision Computing. 2001;19:1023-1040.         [ Links ]

2. Kass M, Witkin A, Terzopoulos D. Snakes: active contour models. International Journal of Computer Vision 1988;1:321-331.         [ Links ]

3. Terzopoulos D, Witkin A, Kass M. Constraints on deformable models: recovering 3D shape and nonrigid motion, Artificial Intelligence. 1988;36:91-123.         [ Links ]

4. Fischl B, Dale M. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Science. 2000;97(20):1050-11055.         [ Links ]

5. Carman G, Drury H, Essen D. Computational methods for reconstructing and unfolding the cerebral cortex. Cerebral Cortex. 1995;5:506-517.         [ Links ]

6. Drury H, Van Essen D. Computerized mappings of the cerebral cortex: a multiresolution flattening method and a surface-based coordinate system. Journal of Cognitive Neuroscience. 1996;1:1-28.         [ Links ]

7. Essen D, Drury H. Structural and functional analyses of human cerebral cortex using a surface-based atlas. The Journal of Neuroscience. 1997;17:7079-7102.         [ Links ]

8. Essen D, Drury H, Joshi S, Miller M. Functional and structural mapping of human cerebral cortex: Solutions are in the surfaces. Neuroimaging of Human Brain Function. 1998;95:788- 795.         [ Links ]

9. Drury H, Corbetta M, Shulman G, Van Essen D. Mapping FMRI activation data onto a cortical atlas using surface-based deformation. NeuroImage. 1998;7:728-730         [ Links ]

10. Joshi M, Cui J, Doolittle K, Joshi S, Van Essen D. Brain segmentation and the generation of cortical surfaces. NeuroImage. 1999;9:461-476.         [ Links ]

11. Van Essen D, Drury H, Dickson J. An integrated software suite for surface-based analyses of cerebral cortex. Journal of the American Medical Informatics Association. 2001;8:443-459.         [ Links ]

12. Harwell J, Van Essen D. Integrated software for surface-based analyses of cerebral cortex. NeuroImage. 20001;13:148-152         [ Links ]

13. Fischl M, Sereno M, Tootell R, Dale A. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1999;8:272-284.         [ Links ]

14. Dale A, Fischl M, Sereno M. Cortical surface-based analysis I: Segmentation and surface reconstruction. NeuroImage. 1999;9:179-194.         [ Links ]

15. Fischl B, Sereno M, Dale A. Cortical surface-based analysis II: Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999:9:195-207.         [ Links ]

16. Fischl B, Liu A, DaleA. Automated manifold surgery: Constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Transactions on Medical Imaging. 20001;20:70-80.         [ Links ]

17. Schwartz E, Shaw A, Wolfson E. A numerical solution to the generalized mapmaker's problem: Flattening nonconvex polyhedral surfaces. IEEE Transactions in Pattern Analysis and Machine Intelligence. 1989;11:1005-1008.         [ Links ]

18. E. Wolfson and E. Schwartz, "Computing minimal distances on polyhedral surfaces," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 11, pp. 1001-1005, 1989.         [ Links ]

19. Floater M. Parametrization and smooth approximation of surface triangulations. Computer Aided Geometric Design. 1997;14:231- 250.         [ Links ]

20. Hurdal M, Stephenson K, Bowers P. Cortical surface flattening: A quasi-conformal approach using circle packings. Neuroimage. 2000;15:114-125.         [ Links ]

21. Hurdal M, Stephenson K. Cortical cartography using the discrete conformal approach of circle packings. NeuroImage. 2004; 23:119-128.         [ Links ]

22. Grossmann R, Kiryati N, Kimmel R. Computational surface flattening: A voxel-based approach. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002;24:433-441.         [ Links ]

23. Wang C, Smith S, Yuen M. Surface flattening based on energy model. Computer-Aided Design 2002;34:823-833.         [ Links ]

24. Li J, Zhang D, Lu G, Peng Y. Flattening triangulated surfaces using a mass-spring model. International Journal of Advanced Manufacturing Technology. 2005;25:108-117.         [ Links ]

25. Wang C, Tang K, Yeung B. Freeform surface flattening based on fitting a woven mesh model. CAD Computer Aided Design. 2005;37:799-814.         [ Links ]

26. Wang C, Tang K, Yeung B. Reduce the stretch in surface flattening by finding cutting paths to the surface boundary. Computer-Aided Design. 2004;36:665-677.         [ Links ]

27. Lee A, Sweldens W, Shroder P. MAPS: multiresolution adaptive parameterization of surfaces. Computer graphics and interactive techniques. 1998;1:95-104.         [ Links ]

28. Sheffer A. Parameterization of faceted surfaces for meshing using angle-based flattening. Engineering with Computers. 2001;17:326-337.         [ Links ]

29. Khodakovsky A, Kitke N, Schroder P. Globally smooth parameterizations with low distortion. ACM Transactions on Graphics (TOG). 2003;22:350-357.         [ Links ]

30. Hermosillo H, Faugueras O, Gomes R. Cortex unfolding using level set methods. INRIA: Institut National de Recherche en Informatique et en Automatique, Tech. Rep., 1999.         [ Links ]

31. Tasdizen T, Whitaker R, Burchard P. Geometric surface smoothing via anisotropic diffusion of normals. Visualization 2002;1:15-18.         [ Links ]

32. Pons J, Keriven R, Faugeras O. Area preserving cortex unfolding. In: Medical Image Computing and Computer-Assisted Intervention MICCAI 2004: 7th International Conference, Saint-Malo, France, September 26-29, 2004. Proceedings, Part I, 2004, pp. 376-383.         [ Links ]

33. Stylianou G, Farin G. Crest lines for surface segmentation and flattening. IEEE Transactions on Visualization and Computer Graphics. 2004;10:536-544.         [ Links ]

34. Haker S, Angenent A. Conformal surface parameterization for texture mapping. IEEE Transactions on Visualization and Computer Graphics. 2000;6:181-189.         [ Links ]

35. Haker S, Angenent A, Kikinis S. On the Laplace-Beltrami operator and brain surface flattening. IEEE Transactions on Medical Imaging. 1999;18:700-711.         [ Links ]

36. Ju L, Stern J, Rehm K. Cortical surface flattening using least square conformal mapping with minimal metric distortion. IEEE International Symposium on Biomedical Imaging: Macro to Nano. 2004;1:77-80.         [ Links ]

37. Levy B, Petitjean S, Ray N, Malliot J. Least squares conformal maps for automatic texture atlas generation. In Proceedings of ACM SIGGRAPH'02, 2002.         [ Links ]

38. Wang Y, Gu X, Chan T, Yau S. Intrinsic brain surface conformal mapping using a variational method. Proceedings of SPIE - The International Society for Optical Engineering. 2004;5370:241-252.         [ Links ]

39. Kanai T, Suzuki Y, Himura F. 3D geometric metamorphosis based on harmonic map. 5th Pacific Conference on Computer Graphics and Applications. 1997;1:97-100.         [ Links ]

40. Ramasubramanian M, Mittal A. Three-dimensional metamorphosis using multiplanar representation. IIEEE. 1999;1:270-275.         [ Links ]

41. Zockler M, Stalling D, Hege H. Fast and intuitive generation of geometric shape transitions. Visual Computer. 2000;16:241-253.         [ Links ]

42. Breen D, Whitaker R. A level-set approach for the metamorphosis of solid models. IEEE Transactions on Visualization and Computer Graphics. 2001;7:173-192.         [ Links ]

43. Treece G, Prager R, Gee A. Volume-based three-dimensional metamorphosis using region correspondence. Visual Computer. 2001;17:397-414.         [ Links ]

44. Azariadis P, Aspragathos N. Geodesic curvature preservation in surface flattening through constrained global optimization. Computer- Aided Design. 2001;33:581-591.         [ Links ]

45. Peyre G, Cohen T. Geodesic computations for fast and accurate surface flattening. Eurographics. 2004;2:1-10.         [ Links ]

46. Zhu L, Haker S, Tannenbaum A. Area-preserving mappings for the visualization of medical structures. MICCAI. 2003;4:277-284.         [ Links ]

47. Mori K, Oka H, Kitasaka T. Virtual unfolding of the stomach based on volumetric image deformation. MICCAI. 2004; 3217:389-396.         [ Links ]

48. Ashburner J, Computational neuroanatomy. 1 ed. London: University College London; 2000.         [ Links ]

49. Windreich G, Kiryati N, Lohmann G. Voxel-based surface area estimation: From theory to practice. Pattern Recognition. 2003; 36:2531-2541.         [ Links ]

50. Chung M, Worsley J, Robbins S. Deformation-based surface morphometry applied to gray matter deformation. NeuroImage. 2003;18:198-213.         [ Links ]