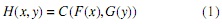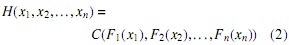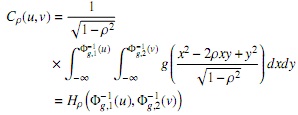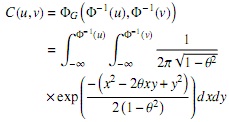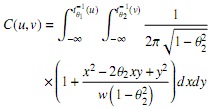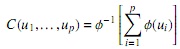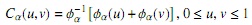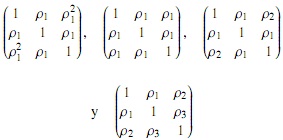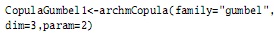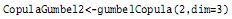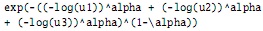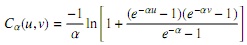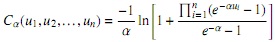Construcción de Distribuciones Multivariadas con Marginales Dependientes Usando Cópulas en R

Construction of Multivariate Distributions with Dependent Marginals Using Copulas in R

M. C. Jaramillo-Elorza^a,*
J. A. Lozano^b,*

^a,* Profesor Asociado, Escuela de Estadística, Universidad Nacional de Colombia-Medellín, Colombia.
^b,* Estudiante de Maestría en Estadística, Universidad Nacional de Colombia-Medellín, Colombia. Correo electrónico: mcjarami@unal.edu.co.

Recepción: 03-mar-13 Aceptación: 27-mar-13

Resumen

Las cópulas se han convertido en una herramienta popular para la construcción de modelos multivariados en campos donde la dependencia multivariada es de gran interés. El propósito de este trabajo es presentar las cópulas tanto en su concepto teórico, como en su implementación en el software estadístico R y profundizar en la construcción de distribuciones multivariadas con marginales dependientes, usando la clase mvdc del paquete copula, la cual permite utilizar varias y diferentes marginales ya implementadas. Además, se trabajará con métodos para dibujar representaciones de perspectiva y contorno para las funciones de distribución y densidad.

Palabras clave: Análisis Multivariado, Cópulas en R, Paquete copula, Software R.

Abstract

The copula has become a popular tool to build the multivariate models, in many fields where the multivariate dependence is of a great interest. This paper purpose is to present the copula both in their theoretical concept and its implementation in the R statistical software, and to deepen into the multivariate distributions? construction with the dependent marginal, by using the copula package’s mvdc class, which allows to use the marginal in several and different types, that have been implemented already. In addition, to work with the methods for drawing the perspective and the contour representations for the distribution and the density functions.

Key words: Copula, Copula package, Multivariate Analysis, R Software.

1. Introducción

Las cópulas se han convertido en una herramienta popular para la construcción de modelos multivariados en campos donde hay un gran interés por la dependencia multivariada; más específicamente, han sido utilizadas en campos tan variados como en medicina, para modelar el número de casos mensuales de una enfermedad casi erradicada, por ejemplo, la poliomielitis [1]; en ciencias actuariales, para modelar la mortalidad y las pérdidas dependientes [2,3]; en finanzas, para análisis y gestión de riesgos [4,5]; en estudios biomédicos, en el modelado de tiempos de eventos correlacionados y riesgos competitivos [6], y en ingeniería, en el control de procesos multivariados y en el modelado hidrológico [7].

En [8] se describen las cópulas como "... funciones de distribución multivariada que unen o ‘copulan’ sus funciones de distribución marginales unidimensionales", y como "... funciones de distribución multivariada cuyas marginales unidimensionales son uniformes en el intervalo [0,1]". Las cópulas son muy útiles a la hora de derivar distribuciones conjuntas, conociendo las distribuciones marginales, especialmente cuando las variables son no normales; por otro lado, se utilizan en un contexto bivariado para definir medidas no paramétricas de dependencia [9].

Una idea más formal de lo que es una cópula se da al considerar un par de variables aleatorias X y Y con funciones de distribución marginales F(x) = P[X ≤ x] y G(y) = P[Y ≤ y], respectivamente, y función de distribución conjunta H(x, y) = P[X ≤ x, [Y ≤ y]. Ahora bien, al par de números (x, y) se le puede asociar tres números F(x), G(y)y H(x, y), donde cada uno de ellos pertenece al intervalo [0,1], es decir, a cada (x, y) le corresponde un punto (F(x),G(y)) en el espacio producto [0, 1] ×[0, 1], y a este par ordenado le corresponde un número H(x, y) en [0,1] (ver [8]).

C : [0,1] × [0,1] → [0,1]
(F(x),G(y)) → H(x, y)

Como se demuestra en [8], esta correspondencia, que asigna el valor de la función de distribución conjunta a cada par ordenado de los valores de las funciones de distribución marginales, es de hecho una función de distribución. Tales funciones son cópulas [10]. Más formalmente, en [11] se describe una cópula como una distribución multivariada cuyas marginales son uniformes en [0,1]. Para un vector p-dimensional sobre el cubo unitario, una cópula es

C(u1,..., up) = P(U1 ≤, u1,..., Up ≤ up)

Por otro lado, [12] afirman que el teorema subyacente de las cópulas fue introducido por Sklar, primero en 1959, en un artículo en francés, y luego, en 1973, en un artículo similar en inglés; hay que tener en cuenta que aunque el término cópula fue introducido por Sklar (1959), ideas y resultados similares pueden ser rastreados en varios trabajos, más notablemente en Hoeffding (1940, 1941). Las posibles mejores bandas para estas funciones las estableció [13], quien estudió medidas de dependencia que son invariantes bajo transformaciones estrictamente crecientes.

2. Teorema de Sklar

Para introducir el concepto del teorema de Sklar se hará referencia, inicialmente, al caso bivariado. Sean X y Y variables aleatorias continuas con funciones de distribución F y G , respectivamente, y sea H su función de distribución conjunta; entonces, existe una cópula tal que para todo x, y, reales se tiene

Si F y G son continuas, entonces C es única [8]. Desde otra perspectiva, esto puede ser interpretado de manera inversa, es decir, si C es una cópula, y F y G son funciones de distribución univariadas, entonces es posible determinar la función de distribución conjunta H dada por (1.1), con marginales F y G.

En general, una función de distribución n-variada puede ser determinada con la versión n-variada del Teorema de Sklar:

Sean X1, X1,..., Xn variables aleatorias continuas con funciones de distribución F1, F2,..., Fn, respectivamente, y función de distribución n-dimensional conjunta H. Entonces, existe una n-cópula C tal que para todo vector X real se tiene

Si F1, F2,..., Fn son todas continuas, entonces es única (ver [9]).

Además, como se menciona en el título de este artículo, las marginales deben ser dependientes para que el uso de cópulas en la construcción de distribuciones multivariadas sea útil, ya que si son independientes la distribución conjunta se reduciría solamente al producto de las marginales univariadas.

Para hacer mención de esta dependencia de las marginales se puede hacer referencia a [9], quien, considerando que Cα es una función de distribución con densidad Cα sobre [0, 1] × [0, 1] para α en R y denotando T₁, T₂ los tiempos de falla, y (S 2, S 2), ( f₁, f₂) las respectivas funciones de confiabilidad y de densidad marginales, describe así, a través del modelo cópula, las funciones de confiabilidad y densidad conjuntas de T₁y T₂:

S (t₂, t₂) = Cα(S₁(t₁), S 2(t₂)), t₁, t₂ ≥ 0
f (t₂, t₂) = Cα(S₁(t₁), S 2(t₂)) f₁(t₁) f₂(t₂), t₁, t₂ ≥ 0

donde (T₁, T₂) proviene de una cópula Cα (ver [8]).

Este valor de α es, en realidad, el que une o copula las distribuciones, y está asociado al parámetro de dependencia entre los tiempos de falla T₁ y T₂, el cual puede estar relacionado con la correlación o con alguna clase de matriz de correlación para casos multivariados o, entre otros, con el τ de Kendal, que va a estar completamente determinado por la cópula [14].

Dos de las familias de cópulas más usadas son: las cópulas Elípticas y las Arquimedianas.

3. Familia Elíptica

Esta familia de cópulas se caracteriza por compartir propiedades de la normal multivariada [13], tales como simetría, o el hecho de que la estructura de dependencia esté totalmente determinada por la matriz de correlación; facilitan la obtención de modelos multivariantes para extremos y otras formas de dependencia no normales, y son de gran importancia en finanzas y manejo de riesgos, por su fácil implementación. Se definen como las cópulas asociadas a las distribuciones elípticas por el teorema de Sklar, como, por ejemplo, las cópulas Normales y t-Student. Sean F una c.d.f. de una distribución elíptica multivariada y Fi la c.d.f. de i-ésima marginal, y F⁻¹ su respectiva función inversa, i = 1,..., n, la cópula elíptica determinada por F es

C(u1, u2,..., un) = F(F⁻¹(u1), F⁻¹(u2),..., F⁻¹(un))

Se llama cópula elíptica bivariada a toda cópula de la forma:

La cual es la distribución conjunta de las variables X y Y, Φ⁻¹(u), Φ⁻¹(v), son las respectivas funciones cantiles, y ρ es el coeficiente de correlación entre X y Y.

La cópula normal bivariada tiene la forma:

donde Φ es la c.d.f. de la distribución normal estándar, y φG (u, v) es la distribución normal estándar bivariada con parámetro de correlación θ en (−1, 1) [15] .

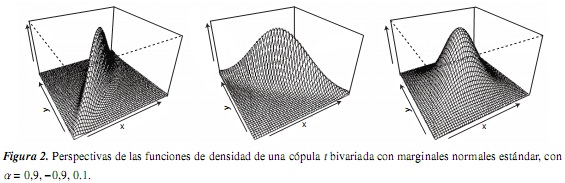
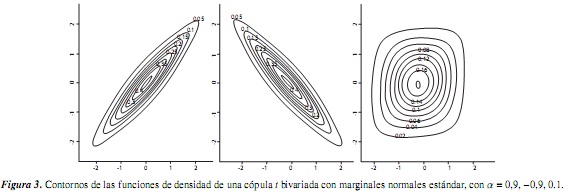
Por otro lado, un ejemplo de una cópula elíptica con dos parámetros de dependencia es la distribución t bivariada con w grados de libertad y correlación ρ:

donde t⁻¹(u) denota la inversa de la c.d.f de la distribución t univariada estándar con θ1 grados de libertad, y t⁻¹_θ2(v) denota la inversa de la c.d.f de la distribución t univariada estándar con θ2 grados de libertad. Los dos parámetros de dependencia son (θ₁,θ₂); θ₁ controla la pesadez de las colas [15].

4. Familia Arquimediana

Las cópulas Arquimedianas no surgieron originalmente en la estadística, aparecieron en el estudio de espacios métricos probabilísticos, donde fueron estudiadas como parte del desarrollo de una versión probabilística de la desigualdad triangular. La selección de esta familia se debe a que se puede simular fácilmente; además, los cálculos de medidas de dependencia se simplifican, lo cual permite una mejor estimación de los parámetros. La distribución multivariada de esta familia para p variables está representada por:

donde φ es el generador de la cópula C. Para el caso de cópulas bivariadas, la familia Arquimediana se representa por (ver [16]):

donde φα se denomina el generador de la cópula Cα, el cual es una función convexa y decreciente tal que φα > 0. Además, su inversa φ⁻¹ _α es la transformada de Laplace de una variable latente denotada τ, la cual induce la dependencia α. La tabla 1 muestra las cópulas que se considerarán de la familia Arquimediana y su espacio parametral:

Además, es necesario tener en cuenta los generadores y el coeficiente de correlación τ de Kendall:

5. Experimental

5.1. Implementación al software R

Las técnicas existentes para estimar distribuciones conjuntas de datos no lineales son a menudo tarea difícil, ya que requieren exigentes procedimientos de estimación computacional basados en simulaciones.

Aunque los fundamentos de las cópulas son complejos o, como se afirma en [17], todavía no son muy fáciles de usar, su implementación práctica y simulación ahora es relativamente sencilla [12].

La implementación de cópulas en paquetes estadísticos es muy escasa en cuanto a variedad, aunque no en desarrollo; por ejemplo, el software comercial Splus cuenta con el módulo finmetrics, que genera números aleatorios de las funciones de densidad y distribución de una cópula bivariada, y las ajusta a unos datos [11]. Dado que este software tiene muchas limitaciones y es comercial, se dificulta el desarrollo de métodos y aplicaciones para cópulas, para lo cual es necesaria una plataforma de uso libre, como lo es R, que funciona en muchas plataformas, genera muy buenas gráficas, ofrece ayuda en línea y cuenta con muchas funcionalidades, como funciones de densidad y distribución multivariadas de la distribución normal y t, las cuales pueden ser usadas para cópulas.

Las ventajas de R llevaron a Yan a diseñar el paquete copula, usando características orientadas a objetos del lenguaje S y del estilo S4 para cópulas elípticas y Arquimedianas. El paquete copula de [11] cuenta con dos clases: copula y mvdc. Para utilizar los códigos que se usarán a continuación, es necesario cargar los paquetes:

y para realizar las ilustraciones es necesario una semilla aleatoria set.seed(1).

5.2. Cópulas Elípticas

En cuanto a las cópulas elípticas, el paquete copula tiene incorporada la clase ellipCopula, en la cual es necesario especificar con qué familia se va a generar la cópula (family), o directamente con normalCopula y tCopula, que, como sus nombres lo dicen, corresponden a las cópulas normal y t, respectivamente. Entre los componentes principales de estas cópulas están la dimensión (dim), el parámetro (param) y la matriz de correlación (dispstr). Siempre que las cópulas sean invariantes bajo transformaciones monótonas de sus marginales, su matriz de correlación determina su estructura de dependencia; las matrices de correlación implementadas en R son auto regresivas de orden 1 (ar1), intercambiables (ex), Toeplitz (toep) y no estructuradas (un), cuyas matrices de correlación, por ejemplo para dimisión 3, son, respectivamente:

donde los ρi’s son parámetros de dispersión; así, dependiendo de cuál matriz de correlación se escoja, se debe introducir un valor o un vector en el componente principal parámetro (param).

Para ilustrar la construcción de este tipo de cópulas, a continuación se muestra un código que crea una cópula trivariada normal y una t con diferentes matrices de correlación:

En esta última se puede observar un componente adicional (df), que corresponde a los grados de libertad de la cópula t.

5.3. Cópulas Arquimedianas

Para la construcción de cópulas Arquimedianas, el paquete copula tiene implementadas la clase general arcmCopula, en la cual se debe especificar la familia por utilizar, como las mostradas anteriormente: Clayton, Frank y Gumbel, y además hay otras, como Joe y amh. Además, otros componentes principales de esta clase son la dimensión (dim) y el valor del parámetro de ella (param), por ejemplo:

en donde se está generando una cópula trivariada Arquimediana de la familia Gumbel con parámetro α = 2. Es necesario tener en cuenta que para dimensiones mayores a 2 solo se admiten asociaciones positivas.

De manera alternativa, se pueden crear cópulas de esta clase llamando directamente las familias antes nombradas de las cópulas Arquimedianas con claytonCopula( ), frankCopula( ), gumbelCopula( ), joeCopula( ) y amhCopula. Así, para la cópula anterior se usaría el código:

5.4. Funciones de densidad y de distribución

En ocasiones puede ser de utilidad o interés acceder a la expresión simbólica de la función de densidad de probabilidad (df) o de la función de distribución acumulada (c.d.f), lo cual en R es muy simple; las funciones de distribución acumulada para los ejemplos anteriores (CopulaGumbel1 y CopulaGumbel2), que son las mismas, dado que son diferentes formas de generar la misma cópula, están dadas por:

CopulaGumbel1@exprdist$cdf

lo cual genera:

CopulaGumbel2@exprdist$cdf

que también genera:

exp(-((-log(u1))ˆalpha + (-log(u2))ˆalpha

+ (-log(u3))ˆalpha)ˆ(1-\alpha))

Ahora, las funciones de densidad de probabilidad para ambas cópulas se generan con los códigos:

CopulaGumbel1@exprdist$pdf
CopulaGumbel2@exprdist$pdf

los cuales generan

Para clarificar y comprobar el resultado de la distribución de la cópula con la tabla 1 es necesario generar una cópula bivariada (dim = 2), como, por ejemplo, una cópula Frank:

donde se observa que R no arroja las funciones simplificadas, sino en su forma general para la dimensión requerida, que al reducirla es equivalente a la presentada en la tabla 1:

De esta forma es fácil deducir, por ejemplo, que para una dimensión de tamaño n la función de distribución de una cópula Frank está dada por:

5.5. Clase mvdc

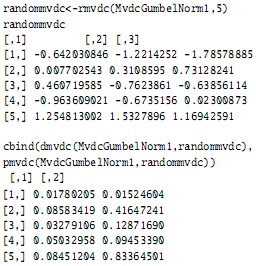
La clase mvdc permite construir distribuciones multivariadas con marginales dadas utilizando cópulas, para lo cual es necesario predeterminar una cópula, como en los ejemplos anteriores. Además, se especifican las funciones de distribución marginales, que pueden estar implementadas en R, o se las puede haber determinado previamente (margins), y estableciendo además cuáles son los parámetros de estas marginales (paramMargins). Por ejemplo, el siguiente código permite construir un objeto mvdc que representa una distribución trivariada con una cópula Gumbel y marginales normales estándar:

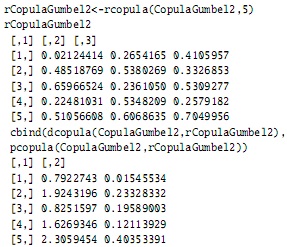
De igual forma, puede ser necesario generar números aleatorios y su evaluación en la función de densidad o de distribución de una cópula, lo cual se obtiene con el siguiente código:

Para realizar esto con objetos mvdc solamente se aplica la función cuantíl a números aleatorios de la cópula en cada marginal, así:

5.6. Gráficas

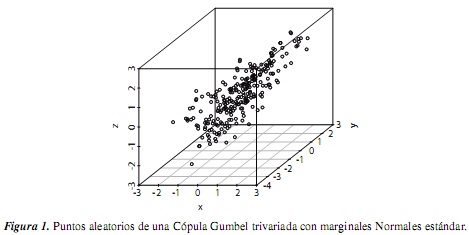
En el campo de la estadística, las gráficas son una potente herramienta de análisis; por ejemplo, para graficar datos de cópulas trivariadas se puede utilizar el paquete scatterplot3d. El siguiente código representa 200 puntos aleatorios de la anterior cópula

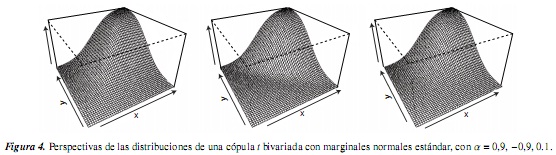
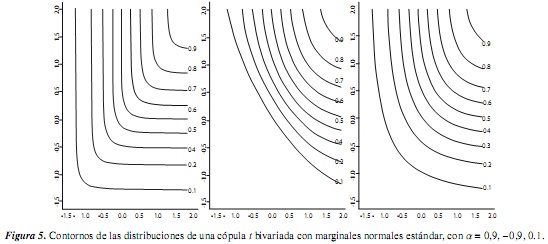
Para los objetos cópula y mvdc, el paquete copula tiene implementados métodos para dibujar representaciones de perspectiva y contorno para las funciones de distribución y densidad; estas funciones son persp y contour. El siguiente código permite representar las funciones de distribución y densidad de una cópula bivariada con marginales normales estándar tanto en contorno como en perspectiva para un param de 0.9:

6. Comentario y conclusiones

Se espera que esta revisión del paquete copula, del software estadístico R, sea de mucha ayuda para las personas que tienen pocos conocimientos del R; el uso de este paquete se debería implementar en los cursos básicos de estadística, en especial, en el curso de estadística multivariada, ya que la estimación de distribuciones conjuntas multivariadas es un campo inexplorado o con soluciones muy delimitadas, y en estos casos el uso de cópulas puede ser de vital importancia en la estimación.

La construcción de distribuciones multivariadas es muy versátil, ya que no requiere que las marginales univariadas, sean del mismo tipo, lo que permite que al momento de utilizarlo en problemas prácticos sea muy aplicable.

La estructura de dependencia utilizada en cópulas de la familia elíptica es más amplia que la de la familia Arquimediana en dimensiones superiores a 2, ya que al momento de analizar o establecer la correlación o dependencia entre cada par de variables, las cópulas Arquimedianas solo permiten establecer, ya sea a partir del τ de Kendall o del α, la misma dependencia para cada par de variables, contrario a lo que pasa con las cópulas elípticas, que permiten diferentes matrices de correlación, algunas de ellas con al menos dos correlaciones diferentes.

Por último, cabe destacar que el acceso gratuito al software estadístico R ha facilitado el uso de las cópulas y, por lo tanto, muchos campos se han visto beneficiados; aunque las bases teóricas de las cópulas no son muy fáciles de utilizar o no son muy amigables, como lo afirmaba [17], ahora se encuentran al alcance de todos.

Referencias

[1] Escarela, H. M. Mena & A. Castillo-Morales, "A Flexible Class of Parametric Transition Regression Models Based on Copulas: Application to Poliomyelitis Incidence", Stat Methods Med Res, vol. 15, no. 6, pp. 593-609, December 2006.         [ Links ]

[2] E. W. Frees & E. A. Valdez, "Understanding Relationships Using Copulas". North American Actuarial Journal, vol. 2, no. 1, pp. 1-25, 1998.         [ Links ]

[3] E. W. Frees & P. Wang, "Credibility Using Copulas". North American Actuarial Journal, vol. 9, no. 2, pp. 31-48, 2005.         [ Links ]

[4] T. Ané, "Dependence structure and risk measure", The Journal of Business, vol. 76, no. 3, pp 411-438, 2003.         [ Links ]

[5] U. Cherubini, E. Luciano & W. Vecchiato, Copula Methods in Finance. John Wiley and Sons, 2004.         [ Links ]

[6] G. Escarela & J. F. Carriere, "Fitting Competing Risks with an Assumed Copula", Stat Methods Med Res, vol. 12, no. 4, pp. 333-349, August 2003.         [ Links ]

[7] C. Genest, & A. C. Favre, "Everything you always wanted to know about Copula Modeling but were afraid to ask", Journal of Hydrologic Engineering, vol. 12, no. 4, pp. 347-368, 2007.         [ Links ]

[8] R. Nelsen, An Introduction to Copulas, 2 edition. New York: Springer; 2006.         [ Links ]

[9] C. Genest & L-P. Rivest, "Statistical Inference Procedures for Bivariate Archimedian Copulas", Journal of the American Statistical Association, vol. 88, no. 423, pp. 1034-1043, sep. 1993.         [ Links ]

[10] C. Genest & J. MacKay, "The joy of copulas: bivariate distributions with uniform marginals". The American Statistician, vol. 40, no. 4, pp. 280-283, 1986.         [ Links ]

[11] J. Yan, "Enjoy the Joy of Copulas: With a Package Copula", Journal of Statistical Software, vol. 21, no. 4, pp. 1-21; Oct 2007.         [ Links ]

[12] P. Trivedi & D. Zimmer, Copula Modeling: An Introduction for Practitioners. World Scientific Publishing, 2007.         [ Links ]

[13] P. Embrechts, F. Lindsborg & A. McNeil, Modelling Dependence with Copulas and Applications to Risk Management, Department of Mathematics ETHZ, Zurich, 2001; disponible en http://www.math.ethz.ch/embrecht/ftp/copchapter.pdf.         [ Links ]

[14] G. Escarela & A. Hernández, "Modelado de parejas aleatorias usando cópulas", Revista Colombiana de Estadística, vol. 32, no. 1, pp. 158, 2009.         [ Links ]

[15] C. Lopera, M. Jaramillo & N. Acosta, "¿Cuándo inicia la enfermedad de Alzheimer? Kaplan Meier versus Turnbull: Una aplicación a datos con censura arbitraria". Revista Colombiana de Estadística, vol. 35, no. 2, pp. 239-254, 2012.         [ Links ]

[16] G. Szegö, "Measures of risk". Journal of Banking and Finance, vol. 26, pp. 1253-1272, 2002.         [ Links ]

[17] W Díaz, Contribuciones a la dependencia y dimensionalidad de cópulas, Tesis de Doctorado, Universidad de Barcelona, Facultad de Biología, Departamento de Estadística, 2012.         [ Links ]