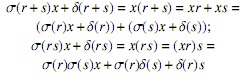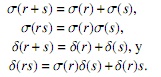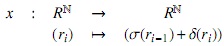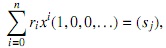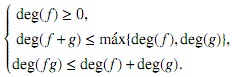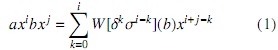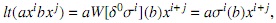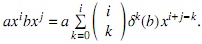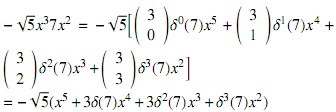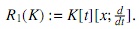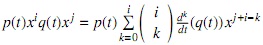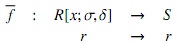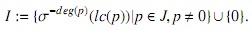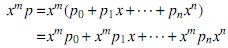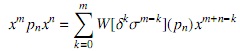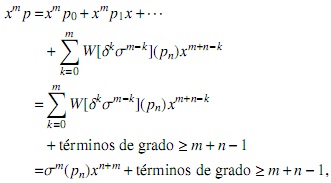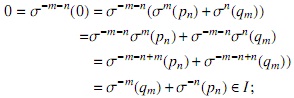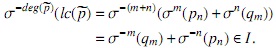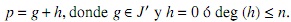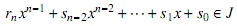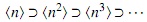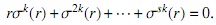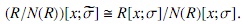Ideales en el Anillo de Polinomios Torcidos R [x;σ,δ]

Ideals in the Skew Polynomials Ring R [x ;σ, δ]

N. R. González Gutiérrez^a,*
Y. P. Suárez Gómez^b

^a,* Docente, Universidad Pedagógica y Tecnológica de Colombia y Estudiante de Doctorado en Ciencias de la Educación - RUDECOLOMBIA - UPTC. Tunja, Boyacá.
^b Docente, Universidad Pedagógica y Tecnológica de Colombia, Tunja, Boyacá. Correo electrónico: nelsy.gonzalez@uptc.edu.co.

Recepción: 08-mar-13 Aceptación: 10-jul-13

Resumen

El presente artículo busca presentar el Teorema de la Base de Hilbert en el anillo de polinomios torcido, algunas clases de ideales que se definen en dicho anillo y qué condiciones son necesarias para que este sea semiprimitivo, además se dan algunos ejemplos de las definiciones para su mejor comprensión. Las demostraciones son tomadas de algunas referencias citadas en el artículo; justificando algunos pasos omitidos en estos textos.

Palabras clave: Anillo de polinomios torcidos (skew), Anillo semiprimitivo, endomorfismo, σ-derivación.

Abstract

This article aims to present the Hilbert’s Basis Theorem for a skew polynomials ring, some classes of ideals that are defined in this ring, and the necessary conditions for an skew polynomials ring to be semiprimitive. Moreover, some examples for the definitions are provided for its better understanding. The proofs of the results in this article are detailed versions of those obtained from the bibliographical references.

Key words: Skew polynomials ring, semiprimitive ring, endomorphism, σ-derivation.

1. Preliminares

El estudio de los anillos de polinomios torcidos tiene su origen en los trabajos de Noether y Schmeidler en 1930, quienes inicialmente los consideraron como anillos de Ore en el contexto de las ecuaciones diferenciales, y como operadores sobre cuerpos finitos.

Resulta interesante estudiar el estado del arte relacionado con los ideales de dicho anillo, es decir, qué relaciones se conservan tomando como referencia el anillo de polinomios clásico y qué condiciones son necesarias para que el anillo de polinomios torcido sea semiprimitivo.

Sea R un anillo con identidad, y sea σ : R → R un endomorfismo de R. Se dice que δ : R → R es una σ−derivación de R si δ es una función aditiva y si r y s son elementos de R, entonces δ(rs) = σ(r)δ(s) + δ(r)s

A continuación se muestra la construcción del anillo de polinomios torcidos a través de un endomorfismo de anillos σ y una σ−derivación δ, dicha construcción es tomada de [2]:

Los anillos de polinomios torcidos pueden ser vistos como los anillos de polinomios sobre R con la indeterminada x donde los coeficientes no necesariamente conmutan con x, es decir, x · r ≠ r · x; induciéndose, de esta forma, la no conmutatividad de ésta clase de anillos. Estos anillos satisfacen las siguientes propiedades:

i) Cada polinomio se expresa de forma única como una suma finita Σ _irixⁱ, con ri ∈ R

ii) xr = σ(r)x + δ(r), para algunos σ(r), δ(r) ∈ R, con r ∈ R, es decir, xr ∈ Rx + R.

Ya que el anillo debe satisfacer que x(r + s) = xr + xs y que x(rs) = (xr)s, se tiene que:

Luego

Por lo tanto tenemos un endomorfismo σ de R y una σ−derivación δ.

Observe que σ(1) = 1 y δ(1) = 0.

Por otro lado, dados R un anillo, σ un endomorfismo sobre R y δ una σ-derivación en R, se construye un anillo que satisfaga las condiciones i) y ii) anteriores. Para ello sea E : = End _Z(R^N), donde R^N : = Π Ri es el producto de los grupos aditivos Ri : = R_i∈N. Así, R → E, identificando cada elemento r ∈ R con el homomorfismo φr, donde φr((ri)) : = (rri). Sea:

donde (ri): = (r0, r1,..., ri,...) ∈ R^Ny r −1: = 0. Se denota con R [x;σ, δ] el subanillo de E generado por x y R (una copia isomorfa de R ). Ahora, si r ∈ R se identifica con el elemento φr ∈ E, se tiene que: xr = σ(r)x + δ(r), de manera que cada f ∈ R [x;σ, δ] se puede expresar como 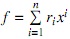Nótese además que:

donde sj = ri si j = i y sj = 0 en otros casos, de modo que la representación de f ∈ R [x;σ, δ] es única.

Así, se ha construido un anillo que satisface las propiedades requeridas.

El grado de un polinomio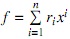es definido i=1 como n siempre que rn ≠ 0, y se denota por deg( f ); lc( f ) = rn se denomina coeficiente principal de f ; lm( f ): = xⁿ es el monomio principal de f , por último lt( f ) = r_nxⁿ se denomina término principal de f . Si los coeficientes ri de f son nulos se dice, que f es el polinomio nulo, de aquí lc( f ): = 0, lm( f ): = 0 y lt( f ): = 0.

El grado de este tipo de polinomios debe cumplir:

También se establece la regla de multiplicación de monomios como sigue:

donde W[δ^kσ^i−k](b) denota la suma de todas las combinaciones posibles entre k veces δ y i − k veces σ evaluadas en b, por ejemplo se tiene que W[δ³σ](b) = δσδ²(b) + δ²σδ(b) + σδ³(b) + δ³σ(b). De aquí se tiene que el producto de monomios no necesariamente es un monomio, el polinomio resultante de este producto tiene como termino principal:

Ejemplo 1. Si σ = i_R se denota a R [x;σ, δ] simplemente como R [x; δ]. Este tipo de anillo se denomina anillo de polinomios con derivación. En este caso,

Ahora si a = − 5 y b = 7, se tiene que

Por otra parte, si δ = 0, se denota a R [x; σ, δ] como R [x; δ], de manera que axⁱbx^j = aσⁱ(b)x^{i+ j}. Estos anillos se denominan anillos de polinomios con endomorfismo. Cuando δ = 0 y σ = i_R se tiene que R [x; σ, δ] = R[x] es el anillo habitual de polinomios en la variable x.

Ejemplo 2. Álgebras de Weyl. Considérese que K es un cuerpo, R : = K [t]y R [x;σ, δ], con σ : = iR y δ : = ^d , es decir, se tiene la K-álgebra

Se tiene entonces xt = tx + 1, xp(t) = p(t)x + d/dt p(t), y en general,

2. Teorema de la Base de Hilbert

El Teorema de la base de Hilbert establece que si R es un anillo noetheriano, entonces el anillo de polinomios, R[x], es un anillo Noetheriano. Resulta entonces interesante extender éste teorema al caso no conmutativo, en el anillo de polinomios torcidos (skew) R [x;σ, δ], a continuación se muestra dicho teorema, dando antes una proposición necesaria para su respectiva prueba.

Proposición 1. Sea σ un automorfismo y R [x;σ, δ] el anillo de polinomios torcidos izquierdo. Entonces, el anillo de polinomios torcidos derecho R [y;σ⁻¹ , −δσ⁻¹] d es isomorfo a R [x;σ, δ].

Demostración. Se probara primero que δ^’= : −δσ⁻¹ es una σ⁻¹-derivación derecha. En efecto, la aditividad es evidente; sean r, s ∈ R, entonces δ^’(rs) = −δσ⁻¹(rs) = −δ(σ⁻¹(r)σ⁻¹(s)) = −σ(σ⁻¹(r))δ(σ⁻¹(s)) − δ(σ¹(r))σ⁻¹(s), es decir, δ^’(rs) = rδ^’(s) + δ^’(r)σ⁻¹(s). Si S : = R [y;σ⁻¹ , −δσ⁻¹] d, entonces la función

es un homomorfismo de anillos el cual satisface que yf (r) = f (σ(r)) y + f (δ(r)) para cada r ∈ R. La propiedad universal de R [x;σ, δ] implica la existencia de un único homomorfismo

para cada r en R y f (xⁱ) = yⁱ para cada i≥ 0. De otra parte, la función g : R → R [x;σ, δ], r → rx⁰, es un homomorfismo de anillos que satisface g(r)x = xg(σ⁻¹(r)) + g(δ^’(r)) para cada r ∈ R. La propiedad universal de S garantiza la existencia de un homomorfismo de anillos g : S → R [x; σ, δ] tal que g(r) = r para cada r ∈ R y g(yⁱ) = xⁱ para cada i ≥ 0. Se obtiene entonces que fg = iS y gf = iR [x;σ,δ], lo que prueba que f es un isomorfismo.

La prueba del siguiente teorema es tomada de [2] dando aquí algunos pasos que son omitidos en este texto.

Teorema 1 (Teorema de la base de Hilbert). Si R es noetheriano a izquierda (derecha) y σ es un automorfismo, entonces R [x;σ, δ] es noetheriano a izquierda (derecha).

Demostración. Suponga que R es noetheriano a izquierda y sea J un ideal izquierdo de R [x;σ, δ]. El teorema es claro si J = 0. Suponga entonces que J ≠ 0 y definamos el siguiente conjunto:

A continuación se probará que I es un ideal izquierdo de R. En efecto; sean σ⁻ⁿpn,σ^−mqm ∈ I con polinomios respectivos p = p0 + p1 x + ··· + pnxⁿ y q = q0 + q1 x + ··· + qmx^m ∈ J. Entonces

utilizando la ecuación (1) con a = 1 y b = pn resulta que:

Ahora reemplazando este término en x^mp se obtiene:

donde σ^m(pn)x^n+m es el termino principal de x^mp_nxⁿ Procediendo de la misma manera se tiene que:

es un polinomio en J. Ahora, si σ^m(pn) + σⁿ(qm) = 0 entonces, como σ es un endomorfismo, σ^k(0) = 0 para cualquier k, además

si σ^m(pn) + σⁿ(qm) ≠ 0, este elemento corresponde al coeficiente principal de p = x^mp + xⁿq ∈ J, y por lo tanto

Por otra parte, dado r ∈ R y p = p0 + ··· + p_nxⁿ ∈ J,σⁿ(r) p ∈ J. Si σⁿ(r) p_n = 0 entonces σ⁻ⁿ(σⁿ(r)p_n) = rσ⁻ⁿ(pn) = 0 ∈ I; si por el contrario σⁿ(r)p_n ≠ 0, entonces σ⁻ⁿ(σⁿ(r)p_n) = rσ⁻ⁿ(p_n) ∈ I. De estos hechos se sigue que I es un ideal izquierdo de R.

Ahora, puesto que R es noetheriano, existen σ⁻ⁿ¹ c1,...,σ^−ntc_t ∈ I tales que I = (σ⁻ⁿ¹ c1,...,σ^−ntct}, donde n_i es el grado del polinomio p_i ∈ J y c_i su coeficiente principal, y p_i = c_ixⁿⁱ + términos de grado ≤ ni−1, para 1 ≤ i ≤ t. Sea n : = m´ax{ni|i = 1,..., t} y defínase J^≠ : = ≠p1,..., pt}, entonces J^≠⊆ J. Sea p ∈ J/{0} con p = cx^m+ términos de grado ≤ m −1; dado que σ^−m(c) ∈ I, σ^−m(c) = s1σ⁻ⁿ¹(c1) + s2σ⁻ⁿ²(c₂) + ··· + stσ^−nt (c_t) para ciertos si ∈ R, 1 ≤ i ≤ t, entonces c = σ^m(s1)σ^m−n1(c₁) + σ^m(s₂)σ^m−n2(c₂) + ··· + σ^m(s_t)σ^m−nt (c_t). Note que p se puede expresar como

En efecto, si deg (p) ≤ n entonces p = 0+ p. Suponga entonces que deg (p) > n y sea

luego p^’= 0 o deg (p^’) < m. Sea g : = σ^m(s₁)x^m−n1 p1 + ...+ σ^m(st)x^m−nt pt, entonces g ∈ J ’y p = g + p ’. Ahora, si p’= 0 entonces p = g + 0 con g ∈ J ’; si por el contrario p’ ≠ 0, se tiene dos opciones: deg (p’) ≤ n ó deg(p ’) > n; en el primer caso ya se tendría la presentación requerida para p. Suponga entonces que deg(p ’) > n; en este caso se repite el procedimiento anterior al polinomio p’∈ J y se encuentra polinomios g’, p" tales que p’= g’+ p" donde g’ ∈ y J’ y p" es tal que p"= 0 ó deg (p") ≤ n o deg (p") > n. De estar en la primera o segunda situación, concluiría la demostración. Si en lugar de esto se tiene el tercer caso, se repite el procedimiento anterior. Se encuentran por tanto polinomios p’, p",... ∈ J tales que deg (p) > deg (p’) > deg (p") >...de manera que, en a lo sumo m − n pasos, se obtiene la descomposición deseada.

Así, se ha mostrado que dado p ∈ J, p = g+ h, donde g ∈ J ’ y h = 0 ó deg (h) ≤ n. En estas condiciones h = p − g ∈ J ∩R (1, x,..., xⁿ}, donde R (1, x,..., xⁿ}denota el R-submódulo de R [x;σ, δ] generado por 1, x,..., xⁿ, visto R [x;σ, δ] como un R-módulo izquierdo. Puesto que R (1, x,..., xⁿ} es un R-módulo izquierdo finitamente generado y R es noetheriano, este módulo resulta ser a su vez noetheriano. Sea M : = J ∩R (1, x,..., xn}, entonces M es también un R-módulo izquierdo finitamente generado pues M ⊆R (1, x,..., xn}; luego M =_R (q(x),..., qs(x)}. Así, dado p ∈ J, p = g + h ∈ J ’+ M, de modo que J ⊆ J ’+ M, pero J ’+ M ⊆ J, luego J = J ’+ M, y así J resulta finitamente generado. De donde R [x; σ, δ] es noetheriano.

Para terminar, suponga que R es noetheriano a derecha, entonces realizando la prueba anterior, pero por el lado derecho para el anillo de polinomios torcidos derechos S : = R [y;σ⁻¹ , −δσ⁻¹], se obtiene que S es noetheriano a derecha, y de la Proposición 1 resulta R [x;σ, δ] noetheriano a derecha.

3. Ideales de R [x;σ, δ]

En las dos siguientes subsecciones se dan algunas propiedades de los ideales en R [x;σ, δ], tomando σ como el endomorfismo identidad, es decir, para r ∈ R se tiene que σ(r) = r y R como un anillo conmutativo con unidad. Algunas de las afirmaciones aquí hechas se toman de [5] y [7]

3.1. Ideales izquierdos de R [x;δ]

Proposición 2. [7, Prop. 2.2] y [6, Prop. 4] Sea K un cuerpo. Todo ideal izquierdo en T = K[x;δ] es principal generado por un polinomio mónico.

Lema 1. [7, Lema 3.1]Sea S = R [x;δ] y sea I = S f (x)S un ideal principal de S donde f (x) = Σⁿ_i=o aixⁱi= 0 es un polinomio de grado mínimo en I. Si δ(a_n R) ⊆ anR, entonces I = S f (x) = f (x)S = f (x)S.

3.2. δ−ideales

Sean δ una derivación en un anillo R e I un ideal de R, entonces I es llamado un δ−ideal si δ(I) ⊆ I. Si R no tiene δ−ideales excepto {0} y R, este es llamado δ−simple.

Ejemplo 3. Sea R el cuerpo de los números reales y R[t] su anillo de polinomios con indeterminada t, d tomando δ(p(t)) = d/dt p(t) y sea (c), c ∈ R, un ideal de R [t] entonces se tiene que δ((c)) =(0) así (c) es un δ−ideal.

Lema 2. [4, Lema 1.3 (i-ii)]Sea δ una derivación de R entonces:

I. Si I es un δ−ideal de R entonces I [x; δ] es un ideal de R [x; δ].

II. Si J es un ideal de R [x; δ], entonces J ∩R es un δ−ideal de R

Lema 3. [5, Lema 2.2] Suponga que n = n · 1 es invertible en R para algún entero n > 0 y que existe un elemento d ∈ R tal que δ(d) es invertible. Si J es un ideal de R [x; δ], entonces J ∩ R es igual al conjunto de los coeficientes de los polinomios p ∈ J.

Demostración. Sea J un ideal de R [x;δ] y sea p =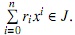

Como

pd −dp = r_nnδ(d)xⁿ⁻¹ + términos de menor grado está contenido en J y nδ(d) es invertible, se tiene que

para algún si ∈ R. Repitiendo este proceso de tiene que r_n ∈ J. Así p−rⁿxⁿ = rn−1 xⁿ⁻¹ + ... + r1 x+ r0 ∈ J. Usando este proceso, se ve que si p = 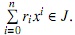entonces los coeficientes de p son elementos de J y así J ∩ R es el conjunto de todos los coeficientes de los polinomios que están en J

Corolario 1. [5, Cor. 2.1] Sea δ’una derivación de R [x; δ], y sea J un ideal de R [x; δ]. Bajo las hipótesis de Lema 3 J es un δ − ideal si y sólo si J ∩ R es un δ^≠−ideal.

Sea Γ el conjunto de todos los δ−ideales de R y Λ el conjunto de todos los ideales de R [x;δ] Entonces se tienen correspondencias: Φ : I ∈ Γ ≠→ I[x; δ] ∈ Λ y Ψ : J ∈ Λ → J ∩R ∈ Γ. Usando está notación se tiene que:

Teorema 2. [5, Thm. 2.1] Suponga que n = n · 1 es invertible en R para cualquier entero n > 0 y que existe d ∈ R tal que δ(d) es invertible. Entonces existe un isomorfismo que preserva el orden de Γ y Λ.

Demostración. Si I₁y I₂ son δ−ideales de R tal que I₁ ⊂ I₂, entonces, por Lema 2, I₁[x;δ] ⊂ I₂[x;δ]. Inversamente, si J₁ y J₂ son ideales de R [x;δ] tal que J₁ ⊂ J₂ , entonces , por Lema 3, J₁ ∩ R ⊂ J₂ ∩ R. Como J₁ ∩ R es el conjunto de todos los coeficientes de polinomios en J₁,ΨΦ = id_Γ y ΦΨ = idΓ y Φ Ψ= id_Λ.

4. Semiprimitividad R [x;σ]

A continuación se toma δ = 0 en el anillo de polinomios torcido, es decir, se toma el anillo de polinomios con endomorfismo, para dar algunas condiciones necesarias para que R [x; σ] sea semiprimitivo (es decir su radical de Jacobson es cero). El radical de Jacobson esta denotado por J(R[x;σ]) y el nilradical por N(R[x;σ]) Algunas de las afirmaciones aquí hechas han sido tomadas de [3] y [4]

Definición 1. Un elemento idempotente i ∈ R se llama central si para todo r ∈ R, ir = ri

Definición 2. Un anillo R se llama un anillo Goldie derecho siempre que cumpla las dos condiciones siguientes:

(I) R satisface la condición de cadena ascendente en anuladores derechos.

(II) R no contiene una suma directa infinita de ideales derechos distintos de cero.

En particular, un anillo noetheriano derecho es un anillo de Goldie derecho.

Ejemplo 4. El anillo de los enteros Zes un anillo de Goldie, ya que es un dominio de ideales principales. Por ejemplo, se puede formar la cadena descendente infinita de ideales:

Definición 3. Un elemento r ∈ R es llamado σ− nilpotente si para todo entero k > 0, existe un entero positivo s = s(r, k) tal que:

Definición 4. Un ideal (izquierdo) I de R es llamado σ-potencia nil, si para cada elemento a ∈ I, existe n = n(a), tal que a es σⁿ− nilpotente.

Para todo anillo con identidad S , se denotara el radical de Jacobson (respectivamente, el radical nilpotente) de S por J(S ) (respectivamente,N(S )).

Teorema 3. Sea R un anillo y σ un automorfismo de R tal que para cada elemento a ∈ R, existe un entero n ≥ 1 tal que σⁿ(a) = a. Si R no tiene nil ideales entonces J(R [x;σ]) = 0

Demostración. Supongamos que J(R [x;σ]) ≠ 0 entonces existe un ideal I ≠ 0 de R el cual es σ^t−nil para algún t ≥ 1. Si todo elemento de I es nilpotente entonces I seria nil ideal, contradiciendo la hipótesis. Supongamos que a ∈ I es no nilpotente. Entonces existe n ≥ 1 tal que σⁿ(a) = a, ya que a ∈ I existe s tal que aσ^nt(a)σ^2nt(a) ...σ^snt(a) = 0. Así a^s+1 = 0 lo cual es una contradicción.

Teorema 4. Sea R la suma directa finita de anillos simples con unidad y σ un automorfismo de R. Entonces J(R[x;σ]) = 0

Demostración. Supongamos que J(R [x;σ] ) ≠ 0 entonces existe un σⁿ−nil ideal I ≠ 0 de R para algún n ≥ 1. Entonces I = eR para algún elemento central e ∈ R. Como σ mapea central en central y R tiene finitos centrales, entonces existe un entero n ≥ 1 tal que σⁿ(e) = e. Pero e ∈ I, así existe s tal que eσⁿ(a)σ²ⁿ(a)···σ^sn(a) = 0. Así e^s+1 = 0 lo cual es una contradicción.

La prueba del siguiente resultado se puede ver en [9].

Teorema 5. Sea R un anillo semiprimitivo de Goldie derecho y σ : R → R un monomorfismo. Entonces J(R [x;σ] ) = 0

Demostración. La prueba de esta teorema se puede ver en [9]

Corolario 2. Sea R un anillo Noetheriano izquierdo que satisface la condición de cadena ascendente sobre anuladores derechos. Sea σ : R → R un monomorfismo. Entonces J(R [x; σ] ) = N(R [x; σ] ) = N(R)[x;σ]

Demostración. Como σ es un monomorfismo y R es noetheriano por [1] se tiene que σ(N(R)) ⊆ N(R). Así N(R)[x;σ] es un ideal de R [x;σ]. Veamos que σ⁻¹(N(R)) = N(R). Para ver esto sea σ(a) ∈ N(R), a ∈ R. Entonces (Rσ(a)R)ⁿ = 0 para algún n ≥ 0. Por consiguiente RaR es un nil ideal de R, así σ⁻¹(N) = N. Sea σ≠un homomorfismo inducido sobre R/N(R), por σ, dado por σ (a + N(R)) = σ(a) + N(R). Entonces σ es inyectivo. Como R/N(R) es un anillo semi-primo ya que N(R/N(R)) = 0 y además es noetheriano izquierdo (en particular de Goldie) y σ es un monomorfismo sobre R/N(R). Por teorema anterior, (R/N(R))[x;σ≠] es semiprimitivo y se tiene que

Así N(R)[x; σ] es un ideal semiprimitivo de R [x; σ] y J(R [x; σ] ) ⊆ N(R)[x; σ]. Puesto que σ(N(R)) ⊆ N(R) y {N(R)}^k = 0 para algún k ≥ 0, (N(R)[x;σ])^k = 0. Así N(R)[x; σ] ⊆ N(R [x;σ] ).

La semiprimitividad de R [x;σ, δ] se puede estudiar de [8] donde σ : R → R es un monomorfismo.

Referencias

[1] T. Y. Lam, Graduate Texts in Mathematics Second Springer A First Course in Noncommutative Rings vol. 131, 2001.         [ Links ]

[2] Lezama, J. O., Extensiones de Ore, Memorias del XVIII Congreso Colombiano de Matemáticas. Universidad Industrial de Santander, Colombia. 2011.         [ Links ]

[3] Mousavi, A., Radicals and prime ideals of skew polynomial rings Augus. In Hahn, S. G. and Suh, D. Y., editors, Proceedings of KAIST mathematics workshop, vol. 7 of Algebra and Topology, pp. 217-230. Korea Advanced Institute of Science and Technology, Mathematics Research Center, August, 1992.         [ Links ]

[4] Jordan, D.A., "NoetherianOre extensions and Jacobson rings", J. London Math. Soc., vol. 2, no. 3, pp. 281-291, 1975.         [ Links ]

[5] Hamaguchi, N. and Nakajima, A., "Derivations of skew polynomial rings", Publ. Inst. Math., vol 72, no. 86, pp. 107-112, 2002.         [ Links ]

[6] Mitsuo, K. and Ken-ichi, Y., "Conditions for an ideal in a polynomial ring to be principal", Commun. Algebra, vol. 19, no. 3, pp. 749-766, 1991.         [ Links ]

[7] Chun, J. and Park, J., "Principal ideals in skew polynomial rings", Comm. Korean Math. Soc, vol. 14, no. 4, pp. 699-706, 1999.         [ Links ]

[8] A. Mousavi. Radicals and prime ideals of skew polynomial rings. In S. G. Hahn and D. Y. Suh, editors, Proceedings of KAIST mathematics workshop, volume 7 of Algebra and Topology, pages 217-230. Korea Advanced Institute of Science and Technology, Mathematics Research Center, August, 1992.         [ Links ]

[9] A. Moussavi. On the semiprimitivity of skew polynomial rings. Proc. Edinburgh Math. Soc. no. 2, 36:169-178, 6, 1993.         [ Links ]