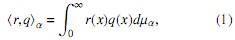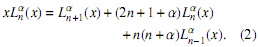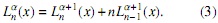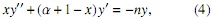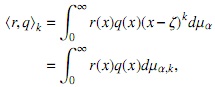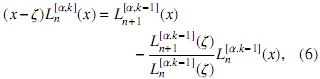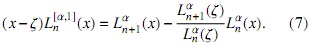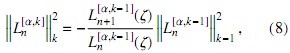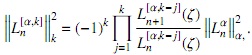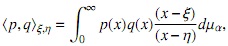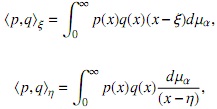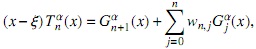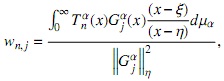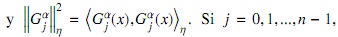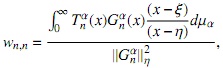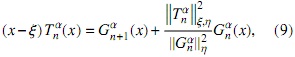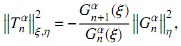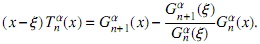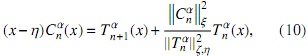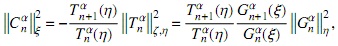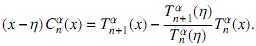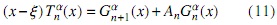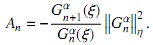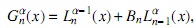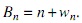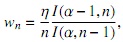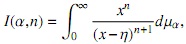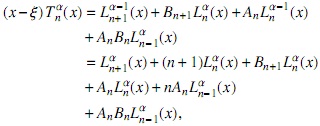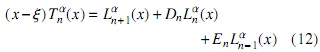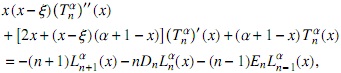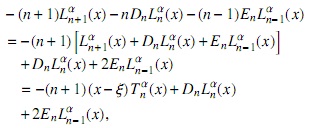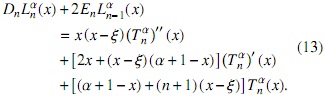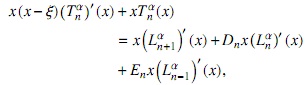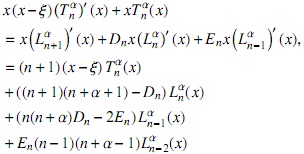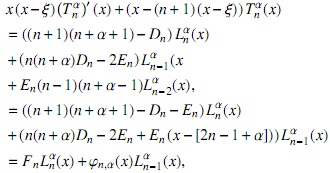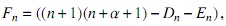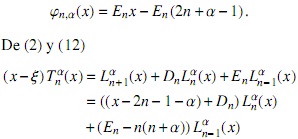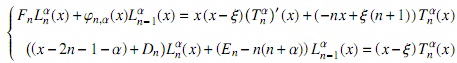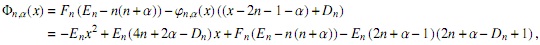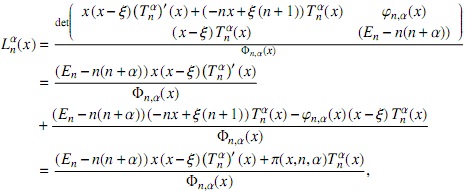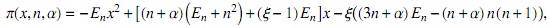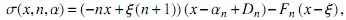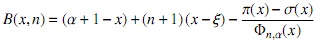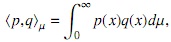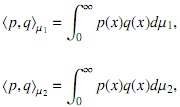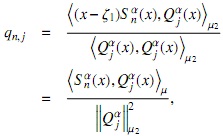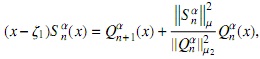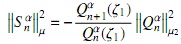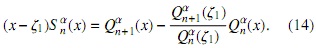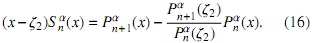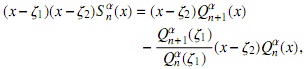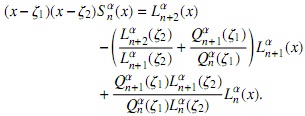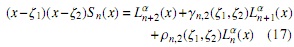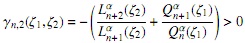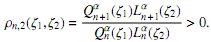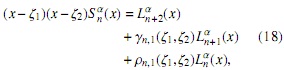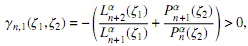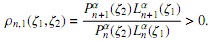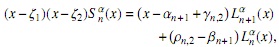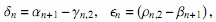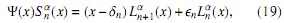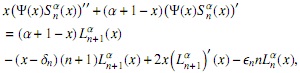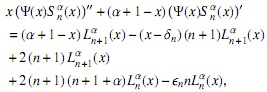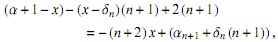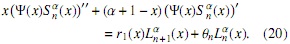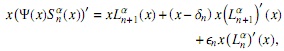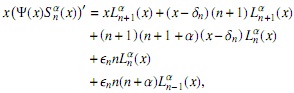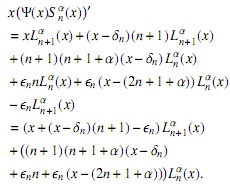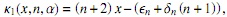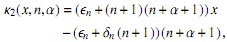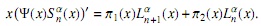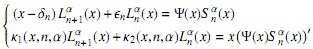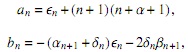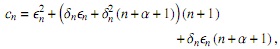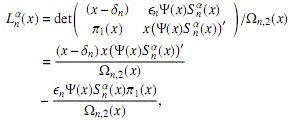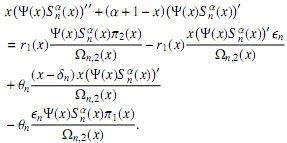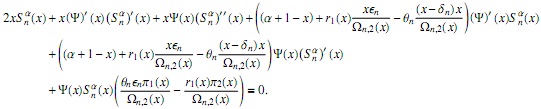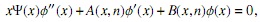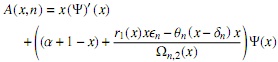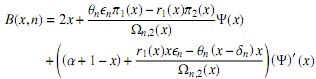Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia en Desarrollo
Print version ISSN 0121-7488
Ciencia en Desarrollo vol.5 no.1 Tunja Jan./June 2014
Ecuaciones Holonómicas Asociadas a Transformacionesónicas del Peso Clásico de Laguerre
Holonomic Equations Associated to Canonical Transformations of the Classical Laguerre Weight
L. A. Molano Molanoa,*
a,* Facultad Seccional Duitama, Universidad Pedagógica y Tecnológica de Colombia, Duitama, Boyacá. Colombia. Correo electrónico: luis.molano01@uptc.edu.co.
Recepción: 26-abr-13 Aceptación: 17-jul-13
Resumen
En este artículo se usan técnicas estándar para encontrar ecuaciones diferenciales satisfechas por polinomios ortogonales asociados a transformaciones canónicas del peso clásico de Laguerre ω(x) = e−x xα, sobre (0, ∞), con α< −1.
Palabras clave: Ecuaciones holonómicas, Polinomios ortogonales clásicos, Transformaciones canónicas.
Abstract
In this paper, it is used the standard techniques to find some differential equations satisfied by orthogonal polynomials, associated with the classical Laguerre weight canonical transformations ω(x) = e−x xα, sobre, on (0, ∞), with α < −1.
Key words: Holonomic Equations, Associated to the Classical, Laguerre Canonical Weight’s, Transformations Weight.
1. Introducción
Sea {pn(x)}n∈N la sucesión de polinomios mónicos ortogonales con respecto al peso clásico de Laguerre ω(x) = e-xxα sobre (0, ∞), con α < −1. En este escrito estamos interesados en estudiar propiedades diferenciales de los polinomios ortogonales con respecto a los pesos ρ(x)ω(x),ρ*(x)ω(x)y ρ**(x)ω(x) donde ρ(x) = 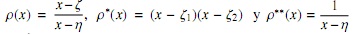 además ζ, ζ1, ζ2 y η son reales negativos. Estas perturbaciones al peso original son conocidas como transformaciones canónicas de tipo Christoffel o Geronimus, y las familias de polinomios ortogonales asociadas a estas han sido ampliamente estudiadas en las últimas décadas, destacando los trabajos [4], [6], [7], [8], [9], [14] y [15], en esencia, relacionados con comportamiento asintótico y localización de ceros. Es bien sabido que las sucesiones clásicas de polinomios ortogonales satisfacen una ecuación diferencial de la forma
además ζ, ζ1, ζ2 y η son reales negativos. Estas perturbaciones al peso original son conocidas como transformaciones canónicas de tipo Christoffel o Geronimus, y las familias de polinomios ortogonales asociadas a estas han sido ampliamente estudiadas en las últimas décadas, destacando los trabajos [4], [6], [7], [8], [9], [14] y [15], en esencia, relacionados con comportamiento asintótico y localización de ceros. Es bien sabido que las sucesiones clásicas de polinomios ortogonales satisfacen una ecuación diferencial de la forma
σ(x)p"(x) + τ(x)p’(x) λn p(x) = 0,
donde σ(x) y τ(x) son polinomios tales que el grado de σ(x) no es mayor a 2 y el de τ(x) es exactamente 1. Esta particularidad es de hecho una característica única de tales sucesiones clásicas. De este modo, resulta interesante estudiar qué tipo de ecuaciones diferenciales (conocidas en la literatura como ecuaciones holonómicas) son satisfechas por los polinomios asociados a las perturbaciones descritas anteriormente, y analizar la naturaleza de sus coeficientes. El conocimiento de la estructura de las ecuaciones diferenciales de segundo orden satisfechas por familias de polinomios ortogonales es la piedra angular en la descripción de modelos electrostáticos asociados a los ceros de tales polinomios (ver [5], [10] o [12]). Son muy conocidas las técnicas estándar que son aplicadas en la obtención de ecuaciones holonómicas asociadas particularmente a perturbaciones del peso clásico, por ejemplo, con las llamadas perturbaciones de Uvarov (ver [2], [3], [11]) o con la perturbación canónica de Christofel ρ(x) = x − ζ al peso de Laguerre ([7]). Nuestro objetivo es adaptar esas técnicas para buscar ecuaciones holonómicas asociadas a las perturbaciones sobre el peso clásico de Laguerre, ya mencionadas. En este sentido, la estructura de este escrito es como sigue. En la sección 2 presentamos los preliminares básicos con respecto a los polinomios de Laguerre clásicos, los cuales nos resultarán muy útiles más adelante; en la sección 3 obtenemos la ecuación holonómica satisfecha por los polinomios asociados a perturbaciones de tipo Geronimus, y en la sección 4 hacemos lo propio con perturbaciones de tipo Christofel.
2. Preliminares
Sea {Lnα(x)}n∈N la sucesión clásica de polinomios mónicos ortogonales de Laguerre, asociada al producto interno
donde dµα = e-xxαdx. Es bien sabido que los ceros de Lαn(x) son reales positivos de multiplicidad 1. Resumimos algunas de las propiedades de esta familia de polinomios ortogonales que serán usadas a lo largo del manuscrito, y cuya prueba puede ser vista en [1] o [13].
Proposición 1. Para cada n ∈ N, los polinomios {Lnα(x)}n∈N satisfacen
- (Relación de recurrencia a tres términos).
- (Relación de estructura)
- Lαn(x) satisface la ecuación diferencial y tiene la propiedad diferencial
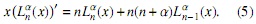
con LαO(x) = 1 y Lα1(x) = x −(α + 1). (escribiremos αn = 2n + 1 + α, y βn = n(n + α))
Sea también 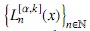 la sucesión de polinomios mónicos ortogonales con respecto al producto interno
la sucesión de polinomios mónicos ortogonales con respecto al producto interno
donde k ∈ Z+ ∪{0} y ζ< 0. Estos polinomios satisfacen la relación (ver [8]),
con Ln [α,0](x) = Lα n(x) y en el caso particular k = 1 entonces tenemos que
De las últimas ecuaciones es fácil ver que se satisface
y en forma recursiva
donde la notación  ,
,  indica la norma inducida por el respectivo producto interno.
indica la norma inducida por el respectivo producto interno.
3. Ecuaciones holonómicas asociadas a perturbaciones de tipo Geronimus
Sea {Tαn}n∈N la sucesión de polinomios mónicos ortogonales con respecto al producto interno
donde ξ y η son reales negativos tales que ξ ≠ η. Además sean {Cαn}n∈N y {Gαn}n∈N la sucesión de polinomios mónicos ortogonales con respecto a los productos y
respectivamente. Si consideramos la base {Gα}n∈N, entonces el polinomio (x-ξ) Tαn(x) puede ser expresado del siguiente modo
donde
entonces wn,j= 0, pero
entonces
y evaluando esta última ecuación ξ en obtenemos
como consecuencia
Podemos hacer lo anterior con el polinomio (x-n)Cnα(x) usando como base la familia{Tαn}n∈N obteniendo
y evaluando esta última expresión en η
para obtener finalmente
Teniendo en cuenta (9) tenemos la ecuación
donde
Encontraremos una ecuación diferencial lineal de segundo orden satisfecha por T αn(x). Para empezar, es importante destacar el trabajo [6], donde se obtuvo la siguiente fórmula de conexión
donde
y la constante wn, (sólo depende del grado del polinomio), tiene la fórmula explícita
donde
y como consecuencia de esta última definición, claramente I(α, n) > 0 y wn < 0. En [6] también es mostrado el comportamiento asintótico de la constante wn, a saber,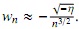 . Empezando con la fórmula (3), tenemos
. Empezando con la fórmula (3), tenemos
entonces
teniendo en cuenta las expresiones de las constantes
Dn= (n+1) + Bn+1 + An
y
En (n+Bn).
Derivando la ecuación (12), multiplicando cada derivada por los factores α + 1 − x y x, respectivamente, y usando (4) tenemos
pero
así
Por otra parte, derivando (12), multiplicando por x y usando (5) tenemos
y mediante el uso de (5) obtenemos
y mediante el uso de (2) llegamos a la expresión
donde
y
y teniendo en cuenta la expresión para Φn,α(x)
entonces obtenemos explícitamente las soluciones
con
y
donde
y finalmente usando (13) tenemos
Resumimos los resultados de la última discusión en la siguiente
Proposición 2. El polinomio Tnα (x) satisface la ecuación diferencial lineal de segundo orden
con
y
4. Perturbaciones de tipo Christofel
Ahora consideremos a {Sαn(x)}n∈N como la sucesión de polinomios mónicos ortogonales con respecto al producto interno
donde dµ=(x-ζ1) (x-ζ2)dµα, y ζ1≠ζ2 son reales negativos. Además sean {Pnα}n∈N y {Qnα}n∈N las sucesiones de polinomios mónicos ortoganeales con respeto a los productos internos y.
respectivamente, con dµ1=(x-ζ1dµα and dµ2=(x-ζ2)dµα. Encontraremos una fórmula de conexión para Snα(x) en términos de los polinomios {Qnα(x)}n∈N usando a la familia {Qnα}n∈N como base, expandimos el polinomio Sn(X)
donde los coeficientes de Fourier vienen dados por
y entonces qn,j= 0, para j= 0,1,...,n-1, así (x-ζ)Snα(x) puede expresarse de la siguiente forma
pero evaluando la última ecuación en ζ1, resulta
así
De la misma forma podemos obtener
y
Mediante el uso de (14) y multiplicando por (x-ζ2) tenemos
y usando (6) resulta
Resumiendo
con
y
Un resultado análogo puede ser obtenido mediante el uso de (16), usando como base la familia {pαn(x)}n∈N, a saber
donde
y
Usando (2) y (18) tenemos
y por simplicidad escribiremos Ψ(x) = (x − ζ1)(x − ζ2),
y así
entonces, derivando, multiplicando por (α + 1 − x)y x,, y usando (4) obtenemos
además usando (3) resulta
así
pero
entonces si r1(x) = −(n + 2) x + (αn+1 + δn (n + 1)) y θn = βn+1 − ∈nn
De nuevo, tomando derivadas en (19) y multiplicando por x
ahora, mediante la fórmula (3)
y usando (2)
entonces, si definimos
y
tenemos
Esta última ecuación junto a (19) forman un sistema de ecuaciones con incógnitas Lαn+1 (x)y Lαn+1(x), a saber
entonces, si son usadas las expresiones de κ1(x, n ,α) y κ2(x, n, α), y después de extensos cálculos, si
donde
y
las soluciones del sistema son explícitamente
y
finalmente, reemplazando las soluciones en (20), tenemos
agrupando y simplificando
Resumimos los resultados en la siguiente
Proposición 3. El polinomio S αn(x) satisface la ecuación diferencial de coeficientes racionales
donde
y
Agradecimientos
El autor agradece los comentarios y las sugerencias hechos por el árbitro anónimo.
Referencias
[1] T.S. Chihara, An introduction to Orthogonal Polynomials, Gordon and Breach, New York, 1978. [ Links ]
[2] H. Dueñas and F. Marcellán, "The Laguerre- Sobolev-type orthogonal polynomials. Holonomic equation and electrostatic interpretation", Rocky Mountain J. Math, vol. 41, pp. 95-131, 2011. [ Links ]
[3] H. Dueñas and F. Marcellán, "The holonomic equation of the Laguerre-Sobolev-type orthogonal polynomials: a non-diagonal case", J. Differ. Equa. Appl. vol. 17, No. 6, pp. 877-887, 2011. [ Links ]
[4] S. Elhay, J. Kautsky, "Jacobi matrices for measures modified by a rational factor", Numer. Algorithms, vol. 6, pp. 205-227, 1994. [ Links ]
[5] F.A. Grünbaum, "Variations on a theme of Heine and Stieltjes: an electrostatic interpretation of the zeros of certain polynomials", J. Comput. Appl. Math. vol. 99, pp. 189-194, 1998. [ Links ]
[6] B. X. Fejzullahu, "Asymptotics for orthogonal polynomials with respect to the Laguerre measure modified by a rational factor ", Acta Sci. Math. Szeged., vol. 77, No. 1-2, pp. 73-85, 2011. [ Links ]
[7] B. X. Fejzullahu,R. X. Zejnullahu. "Orthogonal polynomials with respect to the Laguerre measure perturbed by the canonical transformations". Integ. Transf. Spec. Funct., vol. 21, pp. 569-580, 2010. [ Links ]
[8] E. Huertas, F. Marcellán, B. Xh. Fejnullahu, R.Xh. Zejnullahu, "On orthogonal polynomials with respect to certain discrete Sobolev inner product", Pacific J. Math. vol. 257, No. 1, pp. 167-188, 2012. [ Links ]
[9] E. J. Huertas, F. Marcellán and F. R. Rafaeli, "Zeros of orthogonal polynomials generated by canonical perturbations on measures ", Appl. Math. Comput., vol. 218, pp. 7109-7127, 2012. [ Links ]
[10] M. E. H. Ismail. "An electrostatics model for zeros of general orthogonal polynomials". Pacific J. Math., vol. 193, pp. 355-369, 2000. [ Links ]
[11] L. A. Molano. "On Laguerre-Sobolev type orthogonal polynomials: zeros and electrostatic interpretation". The ANZIAM J. vol. 55, pp. 3954, 2013. [ Links ]
[12] T. J. Stieltjes, "Sur certain polynômes que vérifient une équation diférentielle linéaire du second ordre et sur la théorie des fonctions de Lamé", Acta Math. vol. 6, pp. 321-326, 1885. [ Links ]
[13] G. Szego, Orthogonal Polynomials, 4th ed. American Mathematical Society Colloquim Publication Series, vol. 23, American Mathematical Society, Providence, RI, 1975. [ Links ]
[14] V. B. Uvarov, "Relation between polynomials orthogonal with different weights (in Russian)", Dokl. Akad. Nauk SSSR, vol. 126, pp. 33-36, 1959. [ Links ]
[15] V.B. Uvarov, "The connection between systems of polynomials that are orthogonal with respect to different distribution functions (in Russian)", Z. Vycisl. Mat. i Mat. Fiz. vol 9, pp. 1253-1262, 1969. (English translation in USSR Comput. Math. Math. Phys. vol. 9, pp. 25-36, 1969). [ Links ]




![Ideals in the Skew Polynomials Ring R [x ;σ, δ]](/img/en/prev.gif)