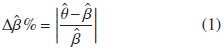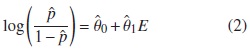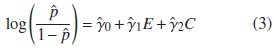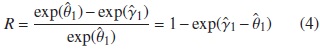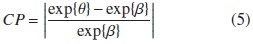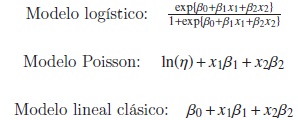Evaluación de la presencia de confusión en algunos miembros de la familia exponencial

Evaluating the Presence of Confounding in Some Members of the Exponential Family

L. M. Acosta Avena^a,*
J. C. Salazar Uribe^b

^aUniversidad de São Paulo, Brasil.
^*Autor de correspondencia: linamav@.ime.usp.br
^bUniversidad Nacional de Colombia, Sede Medellín, Colombia.

Resumen

Una técnica recomendada en la literatura, para detectar si una variable es o no de confusión en un modelo de Cox, es aplicada en algunos modelos de la familia exponencial. El objetivo es determinar si esta técnica es válida en los modelos logístico, Poisson y lineal clásico. Una técnica alternativa, basada en los odds, es propuesta para el caso del modelo logístico. Los resultados muestran que las técnicas tienen un comportamiento similar cuando la confusión está presente en el modelo; sin embargo, la técnica propuesta resultó ser más efectiva en los escenarios en que hay ausencia de este fenómeno.

Palabras clave: Confusión, Familia exponencial, Modelo de Cox, Regresión.

Abstract

A technique to detect confounding, which is recommended in the literature to detect confounders in the Cox models, is adapted and applied to some models of the exponential family. The aim is to assess whether this technique is useful in the logistic, Poisson and linear models. An alternative technique, based on the odds, is proposed for the case of the logistic model. The results show that the techniques have a similar behavior when confusion is present in the model; however, the proposed technique proved to be more effective in scenarios in which this phenomenon was absent.

Key words: Confounding, Exponential Family, Cox Models, Regression.

1. Introducción

El término és "confounding" es usado por los epidemiólogos cuando una covariable está asociada tanto con el resultado de interés y un factor de riesgo principal [7]. La presencia de estas variables puede distorsionar el efecto observado de una exposición sobre un resultado; este efecto se refiere a una aparente relación, cuando la variable de confusión es la causante de la relación; o aparente falta de relación, cuando la variable de confusión atenúa la relación [15]. Por ejemplo, en tablas de contingencia, la asociación que se observa para varios grupos, puede invertir su dirección cuando los datos se combinan en un solo grupo. Esta inversión se conoce como la paradoja de Simpson [9].

Existen en la literatura estadística, varios métodos que permiten evaluar confusión, entre los más comunes se encuentran el riesgo relativo, las razones de odds y las estandarizaciones [1]; otros métodos como aleatorización, restricción y matching son implementados en el diseño de estudio y antes del proceso de recolección de los datos, con el objetivo de controlar este fenómeno [10,11,12]. Una discusión sobre el uso de estos métodos se puede ver Mickey [11] y Kamangar [10].

Otros procedimientos empleados para controlar los factores de confusión en los análisis son, la estratificación y los modelos multivariados [13]. Con la estratificación se trata de buscar grupos dentro de los cuales el factor de confusión no varíe y así evaluar la asociación entre la exposición y la enfermedad dentro de cada estrato del confusor, y luego emplear el estimador de Mantel-Haenszel para ajustar los resultados para cada estrato [13], con este método se determina que hay confusión cuando se encuentran diferencias entre los resultados crudos y los ajustados de acuerdo al estrato. Este método se vuelve poco manejable cuando se tiene un grúmero de estratos o de covariables, o inclusúmero grande de posibles confusores. En estas situaciones es de gran utilidad implementar entonces modelos multivariados.

Wilson [14], Becher [2], Chao [4], Chen [5], Frank [6], Austin [1], entre otros; estudian los efectos que causa la presencia de estas variables en algunos modelos de regresión. Específicamente estudian algunos aspectos importantes en los modelos tales como la estimación de los coeficientes de regresión y sus niveles de confianza, la probabilidad de error tipo I, los residuales, etc. Sin embargo, son pocos los estudios que se centran en los métodos para identificar variables de confusión en modelos de regresión.

Hosmer [8] proponen una técnica para detectar confusión en un modelo de Cox, la cual en adelante llamaremos cambio porcentual, la técnica consiste en comparar los tamaños de los efectos observados en la variable regresora cuando el modelo es ajustado con y sin la variable que es considerada como confusora. Se termina confusión en el modelo cuando existe un cambio superior a 0,20 en los tamaños en los efectos. Otro criterio para detectar confusión se encuentra en Bliss [3], estos autores encuentran que la regla del 10%¹ aplicada a las estimaciones de los odds, proporcionan una técnica simple y de fácil aplicación para determinar confusión en un modelo de regresión logística.

En este artículo es de particular interés estudiar -vía simulación- el comportamiento del criterio del cambio porcentual en los modelos logístico, Poisson y lineal clásico. El objetivo principal de este trabajo es determinar si el criterio es válido para estos modelos. Para esto se asumieron dos variables regresoras de una distribución normal multivariada y en las simulaciones se establecieron diferentes escenarios en los parámetros y tamaños muestrales. Para determinar la eficiencia del criterio en los modelos considerados, se usaron diferentes niveles de referencia.

El desarrollo de este artículo comienza con la sección 2, donde se presenta una descripción de algunos métodos para detectar confusión en modelos de regresión. En la sección 3, se describe el estudio de simulación que se implementó y se discuten los resultados. Finalmente, en la sección 4 se exponen las conclusiones.

2. Metodología

Antes de describir el estudio de simulación implementado en este trabajo, se abordan algunas técnicas utilizadas para identificar variables de confusión en modelos de regresión.

2.1. Algunos criterios para detecar confusión en modelos de regresión

Existen diferentes métodos para detectar la presencia de confusión en modelos de regresión. Entre ellos se encuentran, el criterio del cambio porcentual [8] y la regla del 10 % [3], las cuales serán abordadas en esta sección, así como también el criterio del cambio relativo del odds, propuesto en este artículo.

2.1.1. Criterio de cambio porcentual

Hosmer [8] recomiendan que el porcentaje de cambio en la estimación ajustada se calcula como una medida de la cantidad de ajuste. El estimador del porcentaje de cambio, en general es definido como:

donde θ denota el estimador crudo del modelo que no contiene el potencial confusor y β denota el estimador ajustado del modelo que incluye el potencial confusor.

A pesar de que no existen reglas en el porcentaje de cambio como medida de confusión, Hosmer [8] sugieren que ésta presente en el modelo si la proporción Δβ% es máyor a cualquiera entre [0,15,0,20]. Otros autores [11] recomiendan un nivel convencional de 0,20.

2.1.2. Regla del 10 % aplicada al odds

Basándose en la regla general del 10 %, Bliss [3] evalúan el rendimiento de la regla del 10 % aplicada en los odds ratios de un modelo logístico. De esta manera, los autores ajustan dos modelos de regresión logística: uno dado en la ecuación (2) que incluye sólo a la variable predictora (E) y otro dado por la ecuación (3) que incluye E y C, donde C es el confusor.

Hay evidencia de confusión en este modelo, cuando la diferencia relativa entre las razones de odds, dada por la expresión (4) es superior al ±0,10

2.1.3. Criterio del cambio relativo en el odds

Dada la importancia interpretativa del odds en un modelo de regresión logística, se considera más interesante mirar el efecto que tiene la presencia de una variable de confusión sobre el odds. Así que bajo el mismo enfoque del criterio del cambio porcentual dado por la ecuación (1), se utliza como medida de confusión el cambio relativo en el odds. Por lo tanto el criterio propuesto está queda dado por la siguiente expresión.

donde exp{θ} y exp{β}, denotan los odds del modelo sin ajuste por confusión y con ajuste, respectivamente.

2.2. Estudio de simulación

Con el fin de estudiar el comportamiento del criterio del cambio porcentual en modelos lineales generalizados, se llava a cabo un estudio de simulación en el cuál se consideran tres modelos de la familia exponencial: modelo logístico, modelo Poisson y modelo lineal clásico. En cada modelo, las covariables son generadas de una distribución normal bivariada, con vector de medias cero, y correlaciones ρ = −0,8,−0,6,−0,4,−0,2,0,0,2,0,4,0,6,0,8; tamaños muestrales n = 50,100,200,500 y 1000. Para generar la dependencia entre las covariables y la variable respuesta se utilizó la función de enlace de cada modelo.

por lo tanto se consideraron los siguientes escenarios en los parámetros:

1. En el modelo logístico, los valores conocidos de los parámetros β0,β1,β2 se tomaron de Austin [1], quienes consideran cinco escenarios de acuerdo a un estudio realizado sobre la relación entre el confusor, el factor de riesgo y la probabilidad de observar el resultado de interés. Debido a que en ese estudio, los escenarios 2 y 4 permitían un rango en la probabilidad de la respuesta similar a los escenarios 1 y 5 respectivamente, sólo se asumieron los siguientes

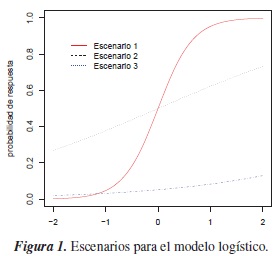
• Escenario 1: β0 = 0,β1 = 0,β2 = 3
• Escenario 2: β0 = 0,β1 = 0,β2 = 0,5
• Escenario 3: β0 = −2,9,β1 = 0,β2 = 0,5

En la figura 1, se observa que con el escenario 1 la probabilidad del resultado permite variar en un rango de muy bajo a muy alto; con el escenario 2 se permiten probabilidades moderadas y, con el escenarios 3 la probabilidad del resultado es baja.

2. En el modelo Poisson, la selección de los parámetros se hace en forma análoga al modelo logístico.

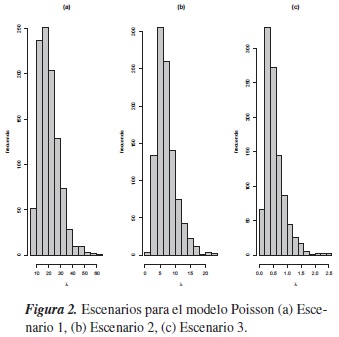
• Escenario 1: β0 = 2,9,β1 = −0,3, β2 = −0,2
• Escenario 2: β0 = 1,9,β1 = 0,1, β2 = 0,4
• Escenario 3: β0 = −0,7,β1 = 0,2, β2 = 0,5

Note en la figura 2 que con el escenario 1 se permite que λ tenga más variabilidad que en el 3 escenario.

3. Para el modelo lineal clásico, se trabajó sólo con un escenario en los parámetros, éstos fueron tomados arbitrariamente.

β0 = −0,6,β1 = 1,3,β2 = 1,4

En las simulaciones el desempeño de (1) y de (5) se evaluó utilizando diferentes niveles de referencia δ = 0,05,0,10,0,15,0,20; este desempeño se determina calculando la proporción de veces en que el veces en la que criterio es inferior a estos niveles.

Debido a que se están asumiendo diferentes grados de correlación entre las variables explicativas, por lo tanto niveles bajos y altos de confusión en el modelo, se determina que el criterio es válido en los modelos mencionados anteriormente si la proporción de veces en la que Δβ%<δ:

• es cercana a cero y ρ →±1, es decir cuando existe un alto grado de confusión en el modelo.


• es cercana a uno y ρ → 0, es decir cuando la confusión no esté presente en el modelo.

3. Resultados y discusión

La presentación de los resultados se desarrolla en dos partes, una para los modelos logístico y Poisson y otra para el modelo lineal clásico. Los resultados en los dos primeros modelos estudiados se encuentran a su vez divididos en los tres escenarios considerados, así mismo, éstos estan divididos por cada nivel de referencia δ.

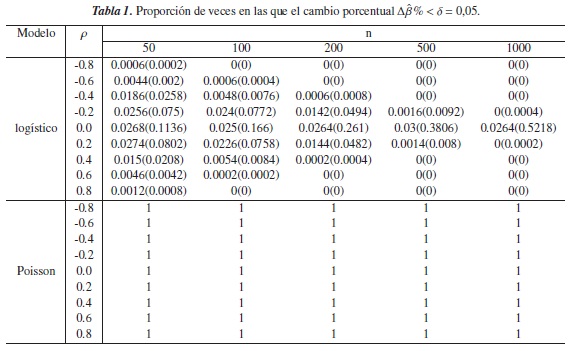
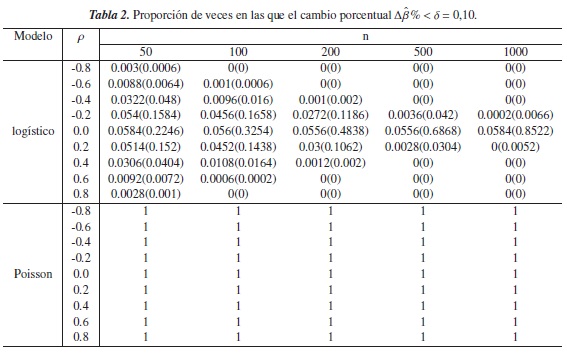
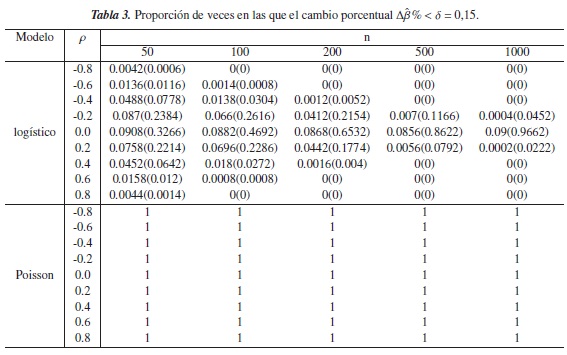
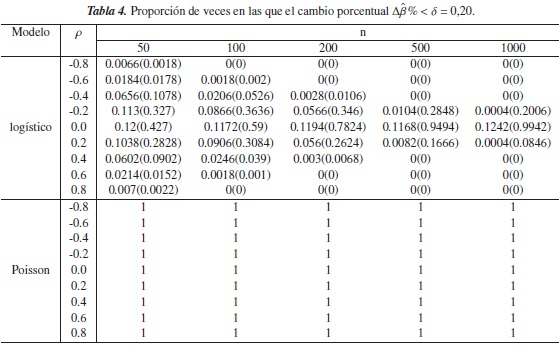
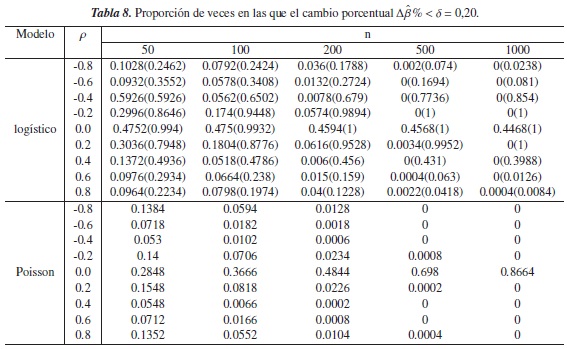
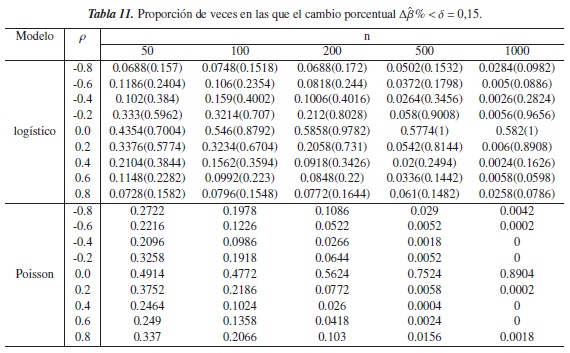
En todas las tablas, los resultados representan la proporción de veces en las que el criterio del cambio porcentual fue inferior a los niveles de referencia asumidos (0.05,0.10,0.15,0.20) para cada modelo, y los resultados que se encuentran entre paréntesis, corresponden a el criterio propuesto para el modelo logístico.

3.1. Modelo logístico y Modelo Poisson

3.1.1. Escenario 1

En las tablas 1 a 4 se presentan los resultados obtenidos para este escenario. En estas tablas se puede observar que para el modelo Poisson, la proporción de veces en las que Δβ% <δ fue exactamente 1, esto sin importar el grado de correlación entre las variables, el tamaño de la muestra y el nivel de referencia δ, indicando con esto que la presencia del fenómeno de la confusión no estaba presente en el modelo cuando realmente lo estaba, por lo tanto, para este modelo y bajo este escenario el criterio no funciona. Sin embargo, cuando ρ= 0 osea cuando no hay confusión, el criterio acertó en todas los modelos que se ajustaron.

En el modelo logístico, los criterios Δβ% y CP se comportan de manera similar y tienen buen desempeño, principalmente cuando existe algún grado de correlación entre las covariables y los tamaños en las muestras aumentan, pues en estos casos las proporciones son cercanas a cero y por tanto logran detectar la presencia de confusión en el modelo. Sin embargo cuando ρ = 0,2 y δ≥ 0,10 el criterio Δβ%es más efectivo que el propuesto, puesto que las proporciones son más bajas y por lo tanto percibe con mayor exactitud la presencia del fenómeno en el modelo.

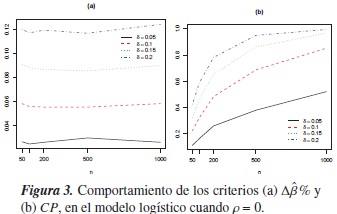
La figura 3 ilustra el comportamiento de los criterios Δβ%y CP cuando en el modelo logístico se simularon covariables con ρ= 0. Se puede observar en la figura 3(a) que la proporción de veces en las que Δβ% <δ es menor a 0,15, señalando con esto que el fenómeno de la confusión se encuentra presente en aproximadamente el 80 % de los modelos, cuando realmente no lo está. En la figura 3(b) las proporciones en las que CP <δ son acercanas a 1 a medida que n y δ aumentan, esto indica que este criterio es más efectivo que el anterior.

3.1.2. Escenario 2

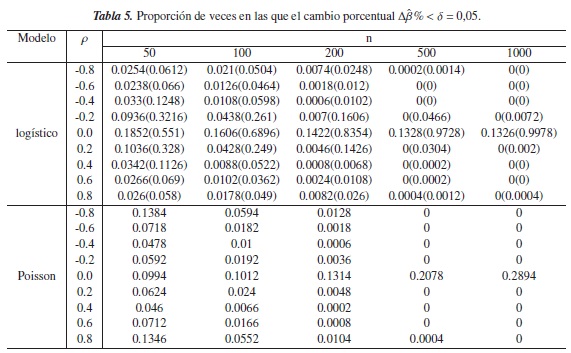
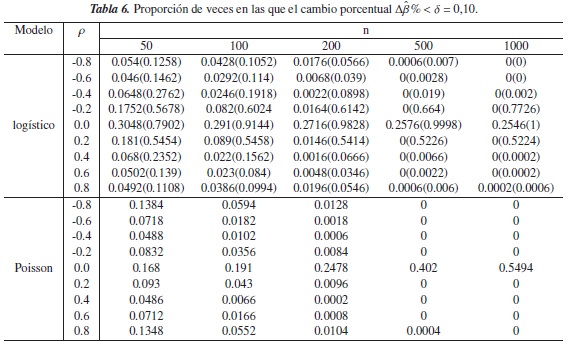
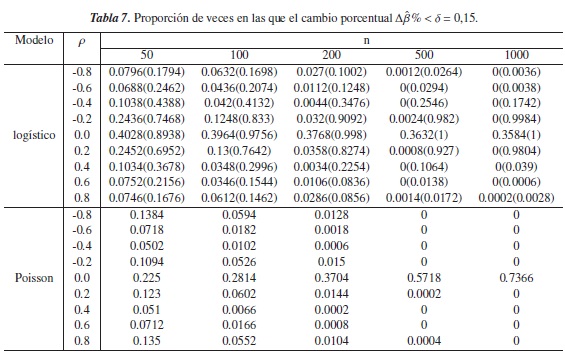
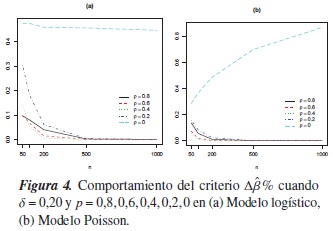
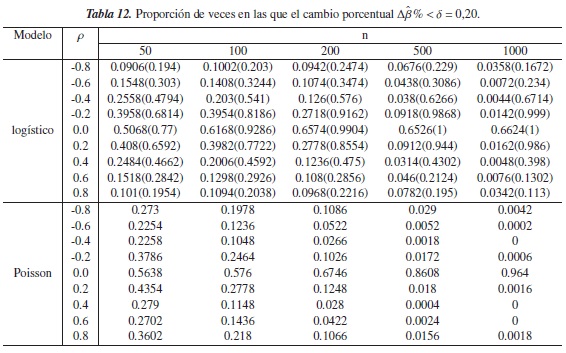
En la tablas de la 5 a 8 se observa que en el modelo Poisson, la proporción de veces en las que Δβ% < δ disminuye a medida de aumenta n y que el grado de correlación entre las variables es más fuerte; esto tal vez se deba a que el modelo se simula con una varianza menor a la que se consideró en el escenario anterior.

La figura 4 muestra el comportamiento del criterio del cambio porcentual propuesto por Hosmer & Lemeshow [8] en ambos modelos cuando δ = 0,20 y correlaciones positivas entre las covariables. Note que en estos casos y para n ≥ 100 el criterio es bastante eficiente en los dos modelos, sin embargo, en el modelo logístico se encuentra que cuando ρ= 0 el criterio no tiene buen desempeño, ya que las proporciones son inferiores a 0,5.

En relación al criterio propuesto se observa que es sensible cuando existe algún grado de correlación entre las covariables y cuando δ aumenta, puesto que la proporción de veces en las que fue menor a δ es bastante alta, indicando que el fenómeno se encuentra en el modelo cuando realmente no está. A manera de ilustración, observe que cuando ρ = ±0,2, sin importar el tamaño de la muestra el criterio no detecta la confusión en más de la mitad de los modelos que fueron realmente simulados con ese fenómeno.

3.1.3. Escenario 3

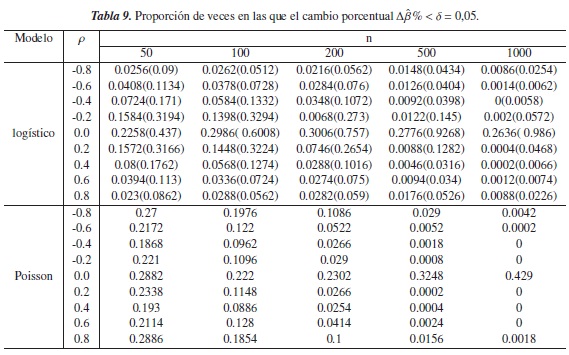
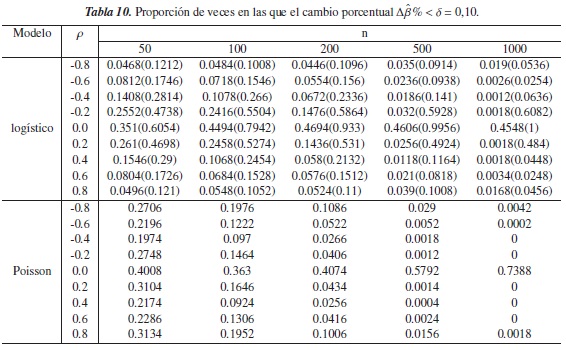
En las tablas 9 y 10 para el modelo logístico, se observa que a medida que el grado de correlación entre las covariables es más fuerte, la proporción de veces en que Δβ% <δ disminuye, y que cuando se aumenta el tamaño de la muestra tienden a ser nula. Este comportamiento también se observa en el modelo Poisson cuando n ≥ 500.

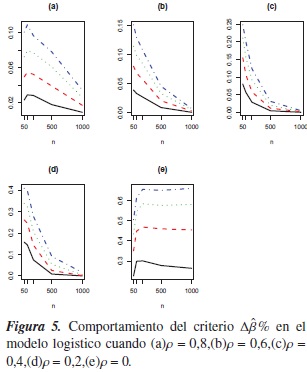
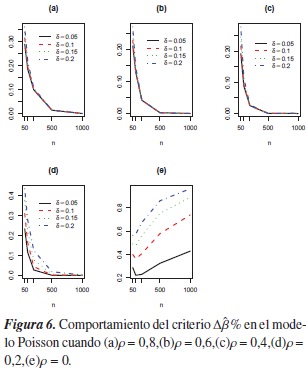
En cuanto a la ausencia de correlación entre las covariables (ρ= 0), se encuentran proporciones más altas en el modelo Poisson, pero al igual que en el modelo logístico, éstas son inferiores a 0,5 cuando δ = 0,05 o δ= 0,10 figura 5(e) y figura 6(e), respectivamente), excepto en el modelo Poisson cuando n ≥ 500 y δ= 0,10; es decir en estos casos Δβ% indica que la confusión está presente en dicho modelo, en más de la mitad de los modelos simulados sin este fenómeno.

En la figura 5, se nota que el criterio Δβ% mantiene un buen desempeño en el modelo logístico y que además mejora cuando ρ = 0, pues a medida de que se aumenta el tamaño de la muestra y el nivel de referencia δ, las proporciones son cada vez más grandes. Cuando p = 0,8,0,6,0,4 en el modelo Poisson, el criterio tiene el mismo comportamiento figura 6(a), (b), (c), mostrando que para n ≥ 500 este criterio tiene un desempeño en este modelo.

Los criterios en estudio tienen comportamientos muy similares cuando en el modelo logístico las covariables se simulan con algún grado de correlación, puesto que en la mayoría de los casos la diferencia entre las proporciones tiende a ser nula, salvo en ρ= −0,2 donde las proporciones de CP llegan a ser superiores a 0,5, mientras que con el criterio Δβ% éstas tienden a cero. Para ρ= 0 las proporciones aumentan cuando n y δ aumentan pero con el criterio propuesto se obtienen valores más cercanos a 1.

3.2. Modelo Lineal clásico

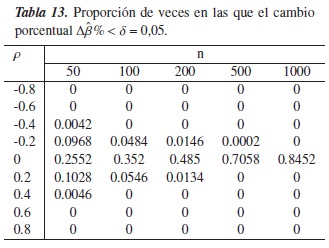
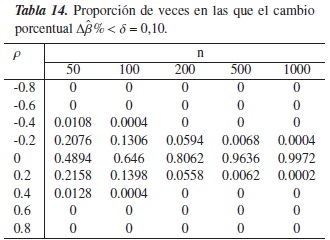
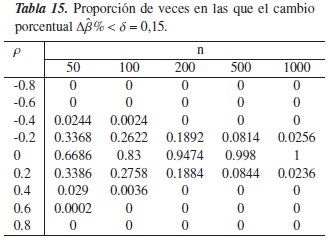
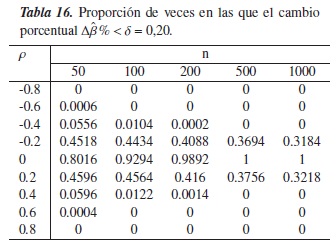
En las tablas 13 a la 16, se muestra el comportamiento del criterio Δβ%cuando se trabaja con un modelo lineal clásico.

Cuando ρ toma valores ±0,8y ±0,6, la proporción de veces en la que Δβ% <δ es nula, esto significa que para los N = 5000 modelos simulados bajo un alto grado de confusión, este criterio detectó que todas el fenómeno realmente estaba presente.

En la figura 7, se observa que a medida que los tamaños muestrales (n) y el nivel de referencia (δ) aumentan y que no existe confusión en el modelo (ρ= 0), el desempeño del criterio mejora. Note por ejemplo en la tabla 15 donde δ = 0,20, el criterio detecta efectivamente la ausencia de confusión en más del 80 % de los modelos simulados, esto sin importar el tamaño en las muestras.

Para ρ± 0,4y n = 50, se observa que Δβ% tiende a equivocarse aproximadamente entre el 1 % y el 6 % de las simulaciones, aunque podría pensarse que este "pequeño error" sucede porque el tamaño de muestra no es lo suficientemente grande, debido a que cuando n ≥ 100, el criterio funciona perfectamente. Análogamente sucede cuando ρ± 0,2, donde el desempeño del criterio es cada vez más bajo cuando se aumenta el nivel de referencia.

4. Conclusiones

En este artículo se evaluó el desempeño del criterio de cambio porcentual propuesto por Hosmer [8] como una posible medida de confusión en modelos de la familia exponencial.

Se encontró que independientemente de la probabilidad del resultado, el nivel de referencia, el tamaño de la muestra y el grado de confusión, el criterio Δβ% mostró tener buen desempeño en el modelo logístico, sin embargo éste tiende a fallar cuando no existe correlación entre las covariables (ρ= 0), principalmente en el escenario 1, donde la probabilidad del resultado se permitía variar en un rango de muy bajo a muy alto. Al igual que el criterio del cambio porcentual, el criterio propuesto tiene un desempeño excelente a lo largo de los escenarios simulados, pero es más confiable para detectar la ausencia de confusión; cuando se emplee este criterio como medida de confusión, se recomienda utilizar un nivel de referencia δ = 0,10.

El principal hallazgo es que cuando se simula la mayor variabilidad en la variable respuesta del modelo Poisson, es decir bajo el primer escenario, el criterio falló completamente en todos los modelos simulados con confusión, incluso con un tamaño de muestra grande. En cambio, el criterio fue efectivo en todos los modelos simulados cuyas covariables tenian ρ= 0.

En forma general, el criterio estudiado mostró a lo largo de los escenarios de simulación, tener mejor desempeño en el modelo lineal clásico, donde un nivel de referencia del 5% es suficiente para que dicho criterio fuera capaz de detectar en más del 90% de las situaciones simuladas con el fenómeno de la confusión; pero para garantizar la veracidad del criterio en situaciones donde no haya confusión, se recomienda utilizar δ= 0,15.

Notas

¹Los tamaños de los efectos observados en los modelos de regresión difieren en una magnitud relativa de al menos el 10%.

Referencias

[1] P. Austin y L. Brunner, "Inflation of the Type I Error Rate When a Continuous Confounding Variable is Categorized in Logistic Regression Analysis", Statistics in Medicine, vol. 23, pp. 1159-1178, 2004.         [ Links ]

[2] H. Becher, "The concept of Residual Confounding in Regression Models and some applications", Statistics in Medicine, 11, pp. 1747-1758, 1992.         [ Links ]

[3] R. Bliss, J. Weinberg, T. Webster y V. Vieira, "Determining the Probability Distribution and Evaluating Sensitivity and False Positive Rate of a Confounder Detection Method Applied To Logistic Regression", J Biom Bioestat, vol. 3, no. 4, pp. 1-14, 2013.         [ Links ]

[4] W. Chao, M. Palta y T. Young, "Efect of omitted Confounders on the Analysis of Correlated Binary Data.", Biometrics, vol. 53, no. 2, pp. 678-689, 1997.         [ Links ]

[5] C. Chen, D.P. Chock y S.L. Winkler, "A Simulation Study of Confounding in Generalized Linear Models for Air Pollution Epidemiology", Environmental Health Perspectives, vol. 107, no. 3, pp. 217-222, 1999.         [ Links ]

[6] K. A. Frank, "Impact of a Confounding Variable on the Inference of a Regression Coefficient", Sociological Methods and Research, vol. 29, no. 2, pp. 147-194, 2002.         [ Links ]

[7] D. W. Hosmer y S. Lemeshow, Applied logistic Regression, John Wiley & Sons, Inc., New York, 2000.         [ Links ]

[8] D. W. Hosmer y S. Lemeshow, Applied Survival Analysis, John Wiley & Sons, Inc., New York, 1999.         [ Links ]

[9] K. Schneiter y J. Symanzik, "An Applet for the Investigation of Simpson's Paradox", Journal of Statistics Education, vol. 21, no. 1, pp. 1-20, 2013.         [ Links ]

[10] F. Kamangar, "Confounding Variables in Epidemiologic Studies: Basics and Beyond", Arch Iran Med, vol. 15, no. 6, pp. 508-516, 2012.         [ Links ]

[11] J. Mickey, y S. Greenland, "A study of the impact of confounder selecction criteria of effect estimation.", American Journal of epidemiology, vol. 129, no. 1, pp. 125-137, 1989.         [ Links ]

[12] S. C. Newman, Biostatistical Methods in Epidemiology, John Wiley & Sons, Inc., New York, 2001.         [ Links ]

[13] M. A. Pourhoseingholi, A. R. Baghestani y M. Vahedi, "How to Control Confounding Effects by Statistical Analysis", Gastroenterol Hepatol Bed Bench, vol. 5, no. 2, pp. 79-83, 2012.         [ Links ]

[14] S. Wilson, y I. Gordon, "Calcutaing Sample Sizes in the Presence of Confounding Variables", Journal of the Royal Statistical Society Series C (Applied Statistics), vol. 35, no. 2, pp.207-213, 1986.         [ Links ]

[15] M. Woodward, Epidemiology. Study Design and Data Analisys, 2 edn, Boca Ratón, Chapman & Hall/CRC,1999.         [ Links ]