Continuidad en estructuras débiles generalizadas

Continuity in Generalized Weak Structures

J. Ávila^a,*
F. Molina^b

^a Universidad del Tolima, Ibagué, Tolima, Colombia.
^b Universidad de Ibagué, Ibagué, Tolima, Colombia.
^* Autor de correspondencia: javila@ut.edu.co

Recepción: 30-abr-15 Aceptación: 07-jun-15

Resumen

En este trabajo se hace un estudio de la continuidad en Estructuras Débiles Generalizadas (EDG), introduciendo la versión local y global de la misma. Además de mostrar varias caracterizaciones, extendemos varios resultados clásicos de topología, topologías generalizadas y estructuras minimales relacionados con axiomas de separación.

Palabras clave: topología generalizada, estructura minimal, estructura débil, estructura débil generalizada, función continua.

Abstract

In this paper we study the continuity in generalized weak structures and we extend to this setting the global and local continuity. We present several characterizations of continuity and we extend some classical topological results related to separation axioms.

Key words: Generalized topology, Minimal structure, Weak structure, Generalized wead structure, Continous function.

1 Introducción

Desde el punto de vista matemático y teórico el estudio de nociones más generales que la estructura topológica ha permitido un desarrollo inusitado de la topología general, en los últimos 15 años. Las topologías generalizadas introducidas por Császár en 1997 [1], han mostrado ser una excelente generalización de topología, evidenciado en las innumerables publicaciones recientes relacionadas con el tema. Por otro lado las estructuras minimales (m-estructruras o m-espacios) introducidas por Maki en 1996 [2] también constituyen otra, no menos importante línea de investigación en este campo, con importantes desarrollos también. Más recientemente Császár en 2011 [3] introdujo las estructuras débiles, las cuales buscan un contexto aún más general donde las nociones topológicas estudiadas en trabajos anteriores puedan seguir siendo válidas. En este sentido Ávila y Molina en 2012 [4] introdujeron las estructuras débiles generalizadas, considerando así el contexto más general posible donde pueden estudiarse las nociones topológicas conocidas. Es importante mencionar que nociones topológicas en colecciones fueron primeramente consideradas en 1999 [5], donde se hace un estudio general, pero amplio, de continuidad, compacidad, conexidad, estructuras iniciales y finales y de los axiomas de separación T₀, T₁ y T₂, entre otras. Aunque en ese trabajo la colección de los conjuntos considerados abiertos es cerrada para uniones, las definiciones de compacidad, separación, conexidad y continuidad se hacen teniendo en cuenta el mayor abierto contenido en el espacio lo cual conduce a resultados bastante interesantes y distintos de los usuales, pero que también generalizan aquellos resultados clásicos.

En este trabajo se generalizan algunos resultados sobre continuidad en m-espacios [6] y topologías generalizadas [7, 8, 9]. Introducimos las versiones local y global y observamos que no son equivalentes. Se presentan varias caracterizaciones de la versión local en términos del g-interior y la g-clausura y se extienden varios resultados que relacionan continuidad con espacios g - T₀, g - T₁ y g - T₂.

2 Nociones básicas

En esta primera parte se presentan algunos resultados y definiciones básicas que se necesitarán en las secciones posteriores. Estos conceptos y otros adicionales pueden consultarse en [4].

Definición 1. Una estructura débil generalizada (EDG) sobre un conjunto X # Ø, es una clase no vacía g de subconjuntos de X.

Si g es una estructura débil generalizada sobre X, entonces al par (X, g) se le llama g-espacio o en algunos casos para simplificar lo llamaremos espacio. Cada elemento de g se llama g-abierto y su complemento g-cerrado.

Al igual que en todos los otros casos citados de topologías, topologías generalizadas y las demás, es posible definir adecuadamente el interior y la clausura de cualquier subconjunto del espacio.

Definición 2. Sean X un g-espacio y A ⊆ X. El g-interior y la g-clausura de A se definen por i_g(A) = ∪{U : U ⊆ A, U ∈ g} y c_g(A) = ∩{F : A ⊆ F, F^c ∈ g}respectivamente.

Nótese que en casos particulares podría tenerse que i_g(X) # X y que c_g(Ø) # Ø. Las principales propiedades de estos operadores, en particular la idempotencia y la monotonía, se presentan a continuación [4].

Proposición 1. Sean g una EDG sobre el conjunto X y A, B ⊆ X. Entonces:

1. i_g(A) ⊆ A.

2. Si A ∈ g, entonces i_g(A) = A.

3. Si A ⊆ B, entonces i_g(A) ⊆ i_g(B).

4. i_g(i_g(A)) = i_g(A).

5. A ⊆ c_g(A).

6. Si A^c ∈ g, entonces c_g(A) = A.

7. Si A ⊆ B, entonces c_g(A) ⊆ c_g(B).

8. c_g(c_g(A)) = c_g(A).

Proposición 2. Sean g una EDG sobre el conjunto X y A ⊆ X. Entonces:

1. i_g(A)^c = c_g(A^c).

2. i_g(A^c) = c_g(A)^c .

3. x ∈ i_g(A), si y sólo si, existe U ∈ g tal que x ∈ U y U ⊆ A.

4. x ∈ c_g(A), si y sólo si, para todo U ∈ g tal que x ∈ U se tiene U ∩ A # Ø.

3 Continuidad en EDG'S

Ahora generalizamos las nociones de función (m, m')-continua y de continuidad generalizada dadas en [6] y [7] respectivamente.

Definición 3. Sean g y g' EDG's sobre X e Y respectivamente. Se dice que una función f : X → Y es (g, g')-continua, si para cada V ∈ g' se tiene que f ^-1(V) ∈ g.

Ejemplo 1.

1. La función identidad i_d : X → X es (g, g')-continua, si y sólo si, g' ⊆ g. En efecto, i_d es (g, g')-continua, si y sólo si, para cada V ∈ g' se tiene que V = i_d^-1(V) ∈ g.

2. Sea {g_α}_α∈Λ una colección de EDG's sobre X. Si f : X → Y es una función (g_α, g')-continua para todo α ∈ Λ, entonces para todo V ∈ g' se tiene que f ^-1(V) ∈ g_α. Así f ^-1(V) ∈∩_α∈Λg_α y por tanto f es (g, g')-continua, donde g = ∩_α∈Λg_α.

La caracterización natural de continuidad en términos de subconjuntos g-cerrados también puede darse en este contexto, como se muestra en la siguiente proposición.

Proposición 3. Sean g y g' EDG's sobre X e Y respectivamente. Una función f : X → Y es (g, g')-continua, si sólo si, la imagen recíproca de cualquier g' -cerrado es un conjunto g-cerrado.

Al igual que en [6]y[8], puede definirse otra noción de continuidad entre EDG's. Esta noción fue orginalmente introducida en [5] en el año 1999.

Definición 4. Sean g y g' EDG's sobre X e Y respectivamente. Se dice que una función f : X → Y es -continua, si para cada x ∈ X y cada V ∈ g' con f (x) ∈ V, existe U ∈ g tal que x ∈ U y f (U) ⊆ V.

En el caso topológico ó más generalmente en contextos donde la colección de abiertos es cerrada para uniones, estas dos definiciones de continuidad resultan ser equivalentes. Sin embargo, cuando las extendemos a conjuntos con EDG's se tiene solamente una implicación como se muestra a continuación. La otra implicación se tiene asumiendo que la EDG del dominio de la función es cerrada para uniones.

Proposición 4. Sean g y g' EDG's sobre X e Y respectivamente. Si la función f : X → Y es (g, g')-continua, entonces también es -continua. El recíproco es cierto si g es cerrada para uniones arbitrarias.

Demostración. Supongamos que f : X → Y es (g, g')-continua y sean x ∈ X y V ∈ g' tales que f (x) ∈ V. Entonces f ^-1(V) ∈ g y x ∈ f ^-1(V), donde f ( f ^-1(V)) ⊆ V. Por tanto, f es -continua.

Recíprocamente, sean x ∈ X y V ∈ g' tales que x ∈ f ^-1(V). Luego f (x) ∈ V. Como f es -continua, existe U ∈ g tal que x ∈ U y f (U) ⊆ V lo que implica que x ∈ U ⊆ f ^-1(V). Así f ^-1(V) es unión de g-abiertos y por la hipótesis, f ^-1(V) ∈ g. '

Siguiendo la demostración del resultado anterior se obtiene la siguiente caracterización de las funciones -continuas. Esta proposición muestra que la diferencia entre las dos nociones de continuidad descansa básicamente en si las colecciones consideradas son o no cerradas para uniones.

Proposición 5. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función. Las siguientes afirmaciones son equivalentes:

1. f es -continua.

2. Para todo g' -abierto A se tiene que f ^-1(A)es unión de g-abiertos.

3. Para todo g' -cerrado C se tiene que f ^-1(C)es intersección de g-cerrados.

Ejemplo 2. En 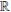, la función i_d : 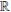→ 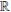donde g = {{x} : x ∈ 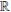} y g' = {(a, b): a, b ∈ 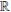}, es una función -continua. Sin embargo, para (a, b) ∈ g' se tiene que i_d^-1((a, b)) = (a, b) no es un conjunto g-abierto. Por consiguiente i_d no es (g, g')-continua. Esto muestra que la -continuidad no implica, en general, la (g, g')-continuidad.

Recordemos que en topología la continuidad está caraterizada por los operadores interior y clausura. En nuestro caso, estas nociones caraterizan las funciones -continuas como se hace en [6] para los m-espacios y en [5] para colecciones.

Proposición 6. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función. Las siguientes afirmaciones son equivalentes:

1. f es -continua.

2. f ^-1(V) = i_g( f ^-1(V)) para todo V ∈ g'.

3. f (c_g(A)) ⊆ c_g' ( f (A)) para todo A ⊆ X.

4. c_g( f ^-1(B)) ⊆ f ^-1(c_g' (B)) para todo B ⊆ Y.

5. f ^-1(i_g' (B)) ⊆ i_g( f ^-1(B)) para todo B ⊆ Y.

6. f ^-1(F) = c_g( f ^-1(F)) para todo F^c ∈ g'.

Demostración. 1 ⇒ 2. Sea V ∈ g' y x ∈ f ^-1(V). Entonces f (x) ∈ V y existe U ∈ g tal que x ∈ U y f (U) ⊆ V. Así x ∈ U ⊆ f ^-1(V). Esto implica que f ^-1(V) ⊆ i_g( f ^-1(V)). Por la Proposición 1, tenemos que i_g( f ^-1(V)) ⊆ f ^-1(V). Por lo tanto f ^-1(V) = i_g( f ^-1(V)).

2 ⇒ 3. Sean A ⊆ X, x ∈ c_g(A)y V ∈ g' tal f (x) ∈ V. Entonces x ∈ f ^-1(V) = i_g( f ^-1(V)). Por la Proposición 2, existe U ∈ g tal que x ∈ U ⊆ f ^-1(V)y U ∩ A # Ø. Entonces Ø # f (U ∩ A) ⊆ f (U) ∩ f (A) ⊆ V ∩ f (A). Por consiguiente, f (x) ∈ c_g' ( f (A)) y por tanto f (c_g(A)) ⊆ c_g' ( f (A)).

3 ⇒ 4. Sea B ⊆ Y, entonces f (c_g( f ^-1(B))) ⊆ c_g' ( f ( f ^-1(B))) ⊆ c_g' (B). Por lo tanto c_g( f ^-1(B)) ⊆ f ^-1(c_g' (B)).

4 ⇒ 5. Sea B ⊆ Y, entonces (i_g( f ^-1(B)))^c = c_g( f ^-1(B^c)) ⊆ f ^-1(c_g' (B^c)) = f ^-1((i_g' (B))^c) = ( f ^-1(i_g' (B)))^c. Por lo tanto f ^-1(i_g' (B)) ⊆ i_g( f ^-1(B)).

5 ⇒ 6. Sea K ⊆ Y tal que K^c ∈ g'. Entonces ( f ^-1(K))^c = f ^-1(i_g' (K^c)) ⊆ i_g( f ^-1(K^c)) = i_g(( f ^-1(K))^c) = (c_g( f ^-1(K)))^c . Por lo tanto c_g( f ^-1(K)) ⊆ f ^-1(K) ⊆ c_g( f ^-1(K)). Así c_g( f ^-1(K)) = f ^-1(K).

6 ⇒ 1. Sean x ∈ X y V ∈ g' tales que f (x) ∈ V. Por 6. tenemos que ( f ^-1(V))^c = f ^-1(V^c) = c_g( f ^-1(V^c)) = c_g(( f ^-1(V))^c) = (i_g( f ^-1(V)))^c . Así f ^-1(V) = i_g( f ^-1(V)). En consecuencia, existe U ∈ g tal que x ∈ U ⊆ f ^-1(V). Por lo tanto x ∈ U y f (U) ⊆ V. '

El siguiente resultado es familiar y nos indica que los dos tipos de continuidad definidas en conjuntos con EDG's se preservan bajo composición de funciones.

Proposición 7. Sean g, g' y g'' EDG's sobre X, Y y Z respectivamente. Si f : X → Y es una función (g, g')-continua (-continua) y h : Y → Z es una función (g', g'')-continua (-continua), entonces la función h ◦ f : X → Z es (g', g'')-continua (-continua).

Demostración. Si V ∈ g'', entonces h^-1(V) ∈ g'. Así f ^-1(h^-1(V)) ∈ g. Ahora bien, (h ◦ f )^-1(V) = f ^-1(h^-1(V)) ∈ g. En consecuencia, h ◦ f es (g, g'')-continua.

Por otro lado, sean x ∈ X y U ∈ g'' tales que (h ◦ f )(x) = h( f (x)) ∈ U. Entonces, existe V ∈ g' tal que f (x) ∈ V y h(V) ⊆ U. Además, existe W ∈ g tal que x ∈ W y f (W) ⊆ V. Por lo tanto, x ∈ W y(h ◦ f )(W) ⊆U.

4 Otras propiedades

En esta sección se presentan algunos resultados que relacionan la continuidad y algunos axiomas de separación. Análogamente a la definición de espacios T₀, T₁ y T₂ usando abiertos, se tienen los respectivos axiomas g -T₀, g -T₁ , g -T₂ usando g-abiertos. Estos resultados extienden resultados bien conocidos en topología, en m-espacios [6] y en topologías generalizadas [8].

Teniendo en cuenta que un espacio es g - T₁ siy solo si cada conjunto unitario es intersección de conjuntos g-cerrados, obtenemos otra caracterización para los espacios g - T₁ .

Proposición 8. Un espacio Y es g - T₁ si y solo si para cada función -continua ((g, g')-continua) f : X → Y, f ^-1({y}) es intersección de g-cerrados para cada y ∈ Y.

Demostración. La suficiencia es clara ya que si y ∈ Y, entonces {y} es intersección de g-cerrados y por tanto f ^-1({y}) es intersección de g-cerrados por la -continuidad de f . Para el recíproco basta tomar la función identidad i_Y : Y → Y. Con esto se tiene que para cada y ∈ Y, i_y^-1({y}) = {y} es intersección de g-cerrados. Así, Y es g - T₁.

Proposición 9. Sean g y g' EDG's sobre X e Y respectivamente con Y un espacio g' - T₁ y f : X → Y una función -continua ((g, g')-continua). Si para A ⊆ X, f (A) = {y} para algún y ∈ Y, entonces f (c_g(A)) = {y}.

Demostración. Basta observar que si f (A) = {y}, entonces A ⊆ f ^-1({y}). Como Y es g' - T₁ entonces {y} es intersección de g'-cerrados. Así f ^-1({y})es intersección de g-cerrados (Proposición 5). Luego c_g(A) ⊆ f ^-1({y}) y esto implica que f (c_g(A)) ⊆{y}. Es decir, f (c_g(A)) = {y} ya que f (A) ⊆ f (c_g(A)).

Proposición 10. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función -continua ((g, g') -continua). Si Y es g' -T₂(g' -T₀, g' -T₁ )y f es inyectiva, entonces X es g - T₂(g - T₀, g - T₁ ).

Demostración. Sean x, y dos puntos distintos de X. Entonces f (x) # f (y). Si Y es g' - T₂, existen g' -abiertos disjuntos U y V tales que f (x) ∈ U y f (y) ∈ V. Por hipótesis existen g-abiertos U_x y V_y tales que x ∈ U_x, y ∈ U_y, f (U_x) ⊆ U y f (V_y) ⊆ V. Como f (U_x) ∩ f (V_y) ⊆ U ∩V = Ø, entonces se concluye que X es g - T₂. La otra parte de la prueba se hace análogamente.

El resto de la demostración es consecuencia directa del hecho que toda función (g, g')-continua es -continua (Proposición 4).

Dadas las EDG's g y g' sobre X e Y respectivamente y f : X → Y, diremos que f es g-abierta si la imagen de cualquier g-abierto en X es unión de g' -abiertos en Y. Con esto puede probarse fácilmente el siguiente resultado.

Proposición 11. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función biyectiva y g-abierta. Si X es g - T₂(g - T₀, g - T₁ ), entonces Y es g' - T₂(g' - T₀, g' -T₁ ).

Recordemos que dada una función f : X → Y el grafo de f está definido como el conjunto G( f ) = {(x, f (x)) : x ∈ X} y el kernel de f está definido como Ker( f ) = {(x, x'): f (x) = f (x')}. Estos dos conjuntos juegan un papel muy importante en algunos resultados topológicos relacionados con los espacios T₂.

Si g y g' son EDG's sobre X e Y respectivamente, entonces sobre X ×Y consideramos la EDG dada por el conjunto g × g= {A × B : A ∈ g y B ∈ g' }.

Proposición 12. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función -continua ((g, g') - continua). Si Y es g' - T₂, entonces G( f ) es intersección de (g × g')-cerrados en X × Y y Ker( f ) es intersección de (g × g)-cerrados en X × X.

Demostración. Sea (x, y) ∈ G( f )^c. Entonces y # f (x) y como Y es g' - T₂, existen g' -abiertos disjuntos U y V tales que y ∈ U y f (x) ∈ V. Como f es -continua existe V_x ∈ g tal que x ∈ V_x y f (V_x ) ⊆ V. Como G( f ) ∩(V_x × U) = Ø entonces V_x × U ⊆ G( f )^c . Así todo punto de G( f )^c es (g × g')-interior y esto implica que G( f )^c es unión de (g × g')-abiertos ó equivalentemente G( f ) es intersección de (g × g')cerrados.

Si (x, y) ∈ Ker( f )^c entonces f (x) # f (y). Luego existen g' -abiertos disjuntos U, V tales que f (x) ∈ U y f (y) ∈ V. Como f es -continua existen g-abiertos U_x y V_y tales que x ∈ Ux, f (Ux) ⊆ U, y ∈ Vy y f (Vy) ⊆ V. Además puede verse fácilmente que Ker( f ) ∩ (U_x × V_y) = Ø. Así U_x × V_y ⊆ Ker( f )^c y esto implica que Ker( f ) es intersección de (g ×g)-cerrados.

Proposición 13. Sean g y g' EDG's sobre X e Y respectivamente y f : X → Y una función sobreyectiva y g-abierta. Si Ker( f ) es intersección de (g × g)-cerrados, entonces Y es g' - T₂.

Demostración. Sean y₁, y₂ ∈ Y con y₁ # y₂. Entonces existen x₁, x₂ ∈ X tales que f (x₁) = y₁ y f (x₂) = y₂. Así (x₁, x₂) ∈ Ker( f )^c y es claro que Ker( f ) es unión de conjuntos (g × g)-abiertos. Entonces existen g-abiertos A y B tales que x₁ ∈ A y x₂ ∈ B. Esto implica que y₁ ∈ f (A)y y₂ ∈ f (B) y cada conjunto f (A) y f (B) es unión de g' -abiertos. Entonces existen g'-abiertos U, V con U ⊆ f (A)y V ⊆ f (B) y tales que y₁ ∈ U y y₂ ∈ V. Como f (A) ∩ f (B) = Ø, entonces U ∩ V = Ø y así Y es g' - T₂.

Dadas las EDG's g y g' sobre X e Y respectivamente y las funciones f, g : X → Y, el igualador defyg es el conjunto eq( f, g) = {x ∈ X : f (x) = g(x)}.

Proposición 14. Sean g y g' EDG's sobre X e Y respectivamente y f, g : X → Y funciones -continuas ((g, g') - continuas). Si Y es g' -T₂, entonces el conjunto eq(f, g) es intersección de g-cerrados.

Demostración. Si z ∈ eq( f, g)^c entonces f (z) ' g(z) y por tanto existen g' -abiertos disjuntos U, V tales que f (z) ∈ U y g(z) ∈ V. Usando el hecho que f y g son -continuas encontramos g-abiertos Uz y Vz tales que z ∈ U_z ∩V_z ⊆ eq( f, g)^c. Es decir, el conjunto eq( f, g)^c es unión de g-abiertos, lo cual implica que eq( f, g) es intersección de g-cerrados.

Si X es un g-espacio, entonces A ⊆ X se llama g-denso si c_g(A) = X. Bajo las hipótesis de la proposición anterior si f (a) = g(a) para todo a ∈ A entonces A ⊆ eq( f, g). Si eq( f, g)^c # Ø entonces existe un g-abierto V ' Ø tal que A ∩ V = Ø. Así A no sería g-denso. Por tanto eq( f, g) = X y así f = g. Es decir, f y g están completamente determinadas por sus valores en conjuntos g-densos.

Un caso particular de la proposición anterior consiste en considerar X un espacio g - T₂y f : X → X una función -continua, entonces se tiene que el conjunto {x ∈ X : f (x) = x} es intersección de g-cerrados. Es decir, el conjunto de puntos fijos de una función -continua de un espacio g - T₂ en sí mismo, es intersección de g-cerrados.

Referencias

[1] A. Császár, "Generalized open sets", Acta Math. Hungar., vol. 75, no. 1-2, pp. 65-87, 1997.         [ Links ]

[2] H. Maki, On generalizing semi-open and preopen sets, Report for Meeting on Topological Spaces and its Applications, Yatsushiro College of Technology, 1996.         [ Links ]

[3] A. Császár, "Weak structures", Acta Math. Hungar., vol. 131, no. 1-2, pp. 193-195, 2011.         [ Links ]

[4] J. Ávila and F. Molina, "Generalized weak structures", Int. Math. Forum, vol. 7, no. 52, pp. 2589-2595, 2012.         [ Links ]

[5] A. Donado, Topología y colecciones, Universidad Pedagógica Nacional, Bogotá, 1999.         [ Links ]

[6] V. Popa and T. Noiri, "On M-continuous functions", Anal. Univ. Dunarea de Jos Galati, Ser. Mat Fiz. Mec. Teor. , Fasc II, vol. 18, no. 23, pp. 31-41, 2000.         [ Links ]

[7] A. Császár, "Generalized topology, generalized continuity", Acta Math. Hungar., vol. 96, no. 4, pp. 351-357, 2002.         [ Links ]

[8] W. Min, "Weak continuity on generalized topological spaces", Acta. Math. Hungar., vol. 124, no. 1-2, pp. 73-81, 2009.         [ Links ]

[9] W. Min, "Generalized continuous functions defined by generalized open sets on generalized topological spaces", Acta. Math. Hungar., vol. 128, no. 4, pp. 299-306, 2010.         [ Links ]