Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia en Desarrollo
Print version ISSN 0121-7488
Ciencia en Desarrollo vol.6 no.2 Tunja July/Dec. 2015
Some Relations between N-Koszul, Artin-Schelter Regular and Calabi-Yau Algebras with Skew PBW Extensions
Algunas relaciones entre álgebras N-Koszul, Artin-Schelter regular y Calabi-Yau con extensiones PBW torcidas
H. Suáreza,*
O. Lezamab
A. Reyesb
a Escuela de Matemáticas y Estadística, Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia.
b Seminario de Álgebra Constructiva -SAC2, Departamento de Matemáticas, Universidad Nacional de Colombia, sede Bogotá, Colombia.
* Autor de correspondencia: hector.suarez@uptc.edu.co
Recepción: 05-ene-15 Aceptación: 15-jun-15
Abstract
Some authors have studied relations between Artin-Schelter regular algebras, N-Koszul algebras and Calabi-Yau algebras (resp. skew Calabi-Yau) of dimension d. In this paper we want to show through examples and counterexamples some relations between these classes of algebras with skew PBW extensions. In addition, we also exhibit some examples of the preservation of these properties by Ore extensions.
Key words: Skew PBW extensions, Calabi-Yau algebras, N-Koszul algebras, AS -regular algebras, Ore extensions.
Resumen
Algunos autores han estudiado las relaciones entre las álgebras Artin-Schelter regular, las álgebras N -Koszul y las álgebras Calabi-Yau (resp. skew Calabi-Yau) de dimensión d. En este artículo queremos mostrar a través de ejemplos y contraejemplos algunos relaciones entre estas clases de álgebras y las extensiones PBW torcidas. Además, mostraremos algunos ejemplos de preservación de estas propiedades en las extensiones de Ore.
Palabras clave: Skew PBW extensions, Calabi-Yau algebras, N-Koszul algebras, AS -regular algebras, Ore extensions.
1. Introduction
Recently there have been defined some special classes of algebras such as N-Koszul algebras, Calabi-Yau algebras and skew PBW extensions. Koszul algebras, which in this article are called 2-Koszul algebras were introduced by Stewart B. Priddy in [34]. Later in 2001, Roland Berger in [3] introduces a generalization of Kozsul algebras, which are then called generalized Koszul algebras or N-Koszul algebras. In [17] Victor Ginzburg defined d-Calabi-Yau algebras or Calabi-Yau algebras of dimension d (or simply Calabi-Yau algebras). Then in [6], Roland Berger and Rachel Taillefer introduced the definition of graded Calabi-Yau algebra. As a generalization of Calabi-Yau algebras, were also defined the skew Calabi-Yau algebras. On the other hand, the skew PBW extensions were introduced in 2011 by Oswaldo Lezama and Claudia Gallego in [16].
In the current literature, it has been studied certain relations between Artin Schelter regular algebras, N-Koszul algebras, Calabi-Yau algebras and skew Calabi-Yau algebras. Our aim is to show through a serie of examples some relationships between the above algebras and skew PBW extensions. Unless otherwise specified, throughout this article, K will represent a fixed but arbitrary field.
2. Definitions and Elementary Properties
2.1. AS -Regular Algebras
Regular algebras were defined by Michael Artin and William Schelter in [2]. They studied the regular algebras of global dimension three which are generated by elements of degree one and classified into thirteen types.
Definition 1 ([2] ). Let A =  ⊕A1 ⊕A2 ⊕··· be a finitely presented graded algebra over K. The algebra A will be called regular if it has the following properties:
⊕A1 ⊕A2 ⊕··· be a finitely presented graded algebra over K. The algebra A will be called regular if it has the following properties:
(i) A has finite global dimension d: every graded A-module has projective dimension ≤ d.
(ii) A has finite Gelfand-Kirillov dimension (GKdim), i.e., A has polynomial growth.
(iii) A is Gorenstein ,i.e., ExtqA( , A) = 0 if q # d, and ExtdA(
, A) = 0 if q # d, and ExtdA( , A) ≅
, A) ≅  .
.
In the current literature these algebras are called Artin-Schlter regular algebras (AS -regular algebras).
Most of the authors do not consider the condition (ii) in the definition of AS -regular algebras. We say that A has polynomial growth if there exist c ∈ ℝ+ and r ∈ℕ such that for all n ∈ℕ, dimK An ≤cnr.
2.2. N-Koszul Algebras
Koszul algebras were defined by Stewart B. Priddy in [34], later in 2001, Roland Berger in [3] introduces a generalization of Koszul algebras which are called generalized Koszul algebras or N-Koszul algebras. Koszul algebras defined by Stewart B. Priddy correspond to 2-Koszul algebras in this paper.
Definition 2 ([3] ). The generalized Koszul algebras are graded algebras A =  ⊕A1 ⊕A2 ⊕··· which are generated in degrees 0 and 1 such that there is a graded projective resolution of
⊕A1 ⊕A2 ⊕··· which are generated in degrees 0 and 1 such that there is a graded projective resolution of 
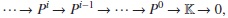
such that for any i ≥ 0, Pi is generated in degree δ(i), where
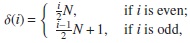
for some N ≥2.
If N = 2, N-Koszul algebras is usually called Koszul. In this situation, Definition 2 coincides with that given by Stewart Priddy in [34].
2.3. Calabi-Yau Algebras of Dimension d
Calabi-Yau algebras of dimension d or d-Calabi-Yau algebras were defined by Victor Ginzburg in [17].
Definition 3 ([17], Definition 3.2.4). A K-algebra A is called a Calabi-Yau algebra of dimension d if
(i) A is homologically smooth; that is, A has a finite resolution of finitely generated projective A-bimodules;
(ii) ExtiA-Bim(A, A⊗A) ≅, as A-bimodules.
The space A ⊗ A is endowed with two A-bimodule structures: the outer structure defined by a ·(x ⊗ y) ·b = ax ⊗yb, and the inner structure defined by a ·(x⊗y) ·b = xb⊗ay. Consequently, the Hom spaces HomA-A(M,A ⊗A) of A-bimodule morphisms from M to A ⊗ A endowed with the outer structure are again A-bimodules using the inner structure of A ⊗A, and the same is true for the Hochschild cohomology spaces Hk(A,A⊗A). For Ae = A⊗Aop, the enveloping algebra of A, each A-bimodule M is a left Ae-module for the action (a⊗b).m = amb and right Ae-module for the action m.(a⊗b) = bma.
Let A = ⊕n∈ZAn be a Z-graded algebra, and M = i∈Z Mi be a graded A-bimodule. For any integer l, M(l) is a graded A-bimodule whose degree i component is M(l)i = Mi+l.
Definition 4. A graded algebra A is called a graded Calabi-Yau algebra of dimension d if
(i) A has a finite resolution of finitely generated graded projective A-bimodules, and
(ii) ExtiAe (A,A ⊗A)≅, as graded A-bimodules; for some integer l.
It follows from Definition 4 that every graded Calabi-Yau algebra of dimension d is Calabi-Yau of dimension d (see [6], Proposition 4.3).
Let M be an A-bimodule, ν , μ: A →A two automorphism, the skew A-bimodule νMμ is equal to M as a vector  -space whit a ·m ·b = ν (a)mμ(b).
-space whit a ·m ·b = ν (a)mμ(b).
Definition 5. Let A be a  -algebra. A is called skew Calabi-Yau of dimension d if there exists an automorphism ν of A such that
-algebra. A is called skew Calabi-Yau of dimension d if there exists an automorphism ν of A such that
(i) A is homologically smooth; and
(ii) ExtiAe (A,Ae) ≅ 0 when i # d and ExtdAe (A,Ae) ≅ 1Aν as Ae-modules.
In this case, ν is called the Nakayama Automorphism of A. The Nakayama automorphism is unique up to an inner automorphism. A ν-skew Calabi-Yau algebra A is Calabi-Yau in the sense of Ginzburg if and only if ν is an inner automorphism of A (see [30], Definition 1.1). So every Calabi-Yau algebra is skew Calabi-Yau.
2.4. Skew PBW Extensions
Skew PBW extensions or σ-PBW extensions were defined in 2011 by Oswaldo Lezama and Claudia Gallego in [16].
Definition 6. Let R and A be rings. We say that A is a skew PBW extension of R if the following conditions hold:
(i) R ⊆ A.
(ii) There exist elements x1,...,xn in A such that A is a left free R-module, with basis,
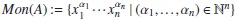
(iii) For each 1 ≤ i ≤ n and any r ∈ R -{0} there exists an element ci,r ∈R -{0} such that
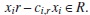
(iv) For any elements 1 ≤i, j ≤n, there exists ci,j ∈ R -{0} such that
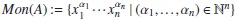
Proposition 1 ([16], Proposition 3). Let A be a skew PBW extension of R. Then, for every 1 ≤ i ≤n, there exist an injective ring endomorphism σi : R →R and a σi-derivation δi : R →R such that
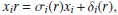
for each r ∈R.
In this case we write A := σ(R)⟨x1,...,xn⟩.
We say that A is a bijective if σi is bijective for each 1 ≤i ≤ n and ci,j is invertible for any 1 ≤i < j ≤ n (see [16], Definition 4).
3. Relations, Examples and Counterexamples
Some authors have found some interesting relations between AS -regular algebras, N-Koszul algebras and Calabi-Yau algebras. Some examples of these relations are the following:
(i) Roland Berger and Nicolas Marconnet in Proposition 5.2 of [8] show that if A = T (V)/⟨R⟩ is a connected graded  -algebra such that the space V of generators is concentrated in degree 1, the space R of relations lives in degrees ≥2, the global dimension d of A is 2 or 3, and that A is AS -regular (the polynomial growth imposed by Artin and Schelter is often removed and in fact, it is not necessary), then A is N-Koszul if d = 3, and 2-Kozul if d = 2.
-algebra such that the space V of generators is concentrated in degree 1, the space R of relations lives in degrees ≥2, the global dimension d of A is 2 or 3, and that A is AS -regular (the polynomial growth imposed by Artin and Schelter is often removed and in fact, it is not necessary), then A is N-Koszul if d = 3, and 2-Kozul if d = 2.
(ii) Roland Berger y Rachel Taillefer in Proposition 4.3 of [6] show than if A is a connected N-graded Calabi-Yau algebra then A is AS -regular algebra, and in Proposition 5.4 they prove that if A is AS -regular C-algebra of global dimension 3 (with polynomial growth), then A is Calabi-Yau if and only if A is of type A in the classification of Artin and Schelter given in [2].
(iii) Let  be of characteristic zero, V be an n-dimensional space with n ≥ 1, w be a non-zero homogeneous potential of V of degree N + 1 with N ≥ 2, and A = A(w) be the potential algebra defined by w (so that the space of generators of A is V); Roland Berger and Andrea Solotar in Theorem 2.6 of [4] pro-ve that if the space of relations R (i.e. the subspace of V⊗N generated by the relations ∂x(w), x ∈ X)of A is n-dimensional, then A is 3-Calabi-Yau if and only if A is N-Koszul of global dimension 3 and dimRN+1 = 1, where RN+1 = (R ⊗ V) ∩ (V ⊗R) ⊆ V⊗(N+1).
be of characteristic zero, V be an n-dimensional space with n ≥ 1, w be a non-zero homogeneous potential of V of degree N + 1 with N ≥ 2, and A = A(w) be the potential algebra defined by w (so that the space of generators of A is V); Roland Berger and Andrea Solotar in Theorem 2.6 of [4] pro-ve that if the space of relations R (i.e. the subspace of V⊗N generated by the relations ∂x(w), x ∈ X)of A is n-dimensional, then A is 3-Calabi-Yau if and only if A is N-Koszul of global dimension 3 and dimRN+1 = 1, where RN+1 = (R ⊗ V) ∩ (V ⊗R) ⊆ V⊗(N+1).
(iv) Manuel Reyes, Daniel Rogalski and James Zhang in Lemma 1.2 of [37] show that if A is a connected graded algebra, then A is graded skew Calabi-Yau if and only if A is AS -regular.
3.1. Examples
In the current literature there are not explicit relations between skew PBW extensions with AS regular algebras, N-Koszul algebras or Calabi-Yau algebras. Next we will show some examples of algebras that are AS -regular, or N-Koszul, or Calabi-Yau, or a combination of these types, that are skew PBW extensions.
3.1.1. AS -regular + N-Koszul + Calabi-Yau
Below are some examples of algebras that are AS regular, N-Koszul and Calabi-Yau, and in addition, they are also skew PBW extensions.
-
The polynomial algebra A =
 [x,y] is a connected graded Noetherian algebra of global dimension 2. It follows that A is AS-regular with GKdim(A) = 2 (see [40], Theorem 3.5), A is 2-Koszul algebra (see [8], Proposition 5.2). Moreover, A is Calabi-Yau of dimension 2 (see [28] ), and A isaskew PBW extension (see [16], Example 5).
[x,y] is a connected graded Noetherian algebra of global dimension 2. It follows that A is AS-regular with GKdim(A) = 2 (see [40], Theorem 3.5), A is 2-Koszul algebra (see [8], Proposition 5.2). Moreover, A is Calabi-Yau of dimension 2 (see [28] ), and A isaskew PBW extension (see [16], Example 5). -
Let A =
 [x1,...,xn] be the polynomial algebra in n variables. Then A is a 2-Kozsul algebra (see [31], Example 1.6), A is a skew PBW extension (see [16], Example 5), A is Calabi-Yau of dimension n (see [9], page 18) and therefore, AS -regular (see [6], Proposition 4.3).
[x1,...,xn] be the polynomial algebra in n variables. Then A is a 2-Kozsul algebra (see [31], Example 1.6), A is a skew PBW extension (see [16], Example 5), A is Calabi-Yau of dimension n (see [9], page 18) and therefore, AS -regular (see [6], Proposition 4.3). -
Let A =
 ⟨x,y,z⟩/⟨yz - zy,zx - xz,xy - yx + z2⟩ which is of type S' in the classification of threedimensional AS -regular algebras given in [2]. According to [8], A is 3-Calabi-Yau (see [45], Example 3.6), and by Proposition 5.2 of [8] A is 2-Koszul. We note that A ℝ σ(
⟨x,y,z⟩/⟨yz - zy,zx - xz,xy - yx + z2⟩ which is of type S' in the classification of threedimensional AS -regular algebras given in [2]. According to [8], A is 3-Calabi-Yau (see [45], Example 3.6), and by Proposition 5.2 of [8] A is 2-Koszul. We note that A ℝ σ( [z] )⟨x,y⟩ and therefore A isaskew PBW extension.
[z] )⟨x,y⟩ and therefore A isaskew PBW extension. -
For any n ≥ 2, let A be a non-degenerate noncommutative quadric graded algebra in n variables x1,...,xn of degree 1. Let z be an extra variable of degree 1. Let B be an algebra defined by a non-zero cubic potential w in the variables x1,...,xn, z. Assume that the graded algebra B is isomorphic to a skew polynomial algebra A[z;σ;δ]over A in the variable z, defined by a 0-degree homogeneous automorphism σ of A and a 1-degree homogeneous σ-derivation δ of A. Then B is 2-Koszul and 3-Calabi-Yau (see [4], Proposition 4.1). B isaskew PBW extension.
3.1.2. AS -Regular + N-Koszul
The following are some examples of AS -regular N-Koszul algebras which are skew PBW extensions. It is not clear if these algebras are Calabi-Yau or not, since we have no clear criteria for making claims in this regard.
-
The algebra A =
 ⟨x,y,z⟩/⟨αβxy + aαβyx, α zx + axz,yz + aβzy⟩ is AS -regular of global dimension 3 of type S1 (see [2], Theorem 3.10). Moreover, A is 2-Koszul (see [8], Proposition 5.2), and A isaskew PBW extension.
⟨x,y,z⟩/⟨αβxy + aαβyx, α zx + axz,yz + aβzy⟩ is AS -regular of global dimension 3 of type S1 (see [2], Theorem 3.10). Moreover, A is 2-Koszul (see [8], Proposition 5.2), and A isaskew PBW extension.
A may be or not Calabi-Yau, depends on the coeffcients a, α and β (see [6], Proposition 5.4). -
The quantum plane A =
 ⟨x,y⟩/⟨yx - cxy⟩ (c # 0) is an AS -regular algebra of global dimension 2 (see [2], page 172), Moreover A is a skew PBW extension as well as 2-Koszul (see [8], Proposition 5.2). For example, if c = 1 then the quantum plane A is a 2-Calabi-Yau algebra.
⟨x,y⟩/⟨yx - cxy⟩ (c # 0) is an AS -regular algebra of global dimension 2 (see [2], page 172), Moreover A is a skew PBW extension as well as 2-Koszul (see [8], Proposition 5.2). For example, if c = 1 then the quantum plane A is a 2-Calabi-Yau algebra. -
The Jordan plane A =
 ⟨x,y⟩/⟨yx - xy - x2⟩ is an AS -regular algebra of global dimension 2 (see [2], page 172). Since A is a quadratic algebra and ⟨yx - xy - x2⟩ is a principal ideal, it follows that A is 2-Koszul (see [15], page 7), A ℝ σ(
⟨x,y⟩/⟨yx - xy - x2⟩ is an AS -regular algebra of global dimension 2 (see [2], page 172). Since A is a quadratic algebra and ⟨yx - xy - x2⟩ is a principal ideal, it follows that A is 2-Koszul (see [15], page 7), A ℝ σ( [x] )⟨y⟩ and therefore A is a skew PBW extension. The Jordan plane A is not Calabi-Yau (see [30]).
[x] )⟨y⟩ and therefore A is a skew PBW extension. The Jordan plane A is not Calabi-Yau (see [30]).
3.1.3. Skew Calabi-Yau algebras
The following is an example of skew Calabi-Yau algebra that is skew PBW extension. Multiparameter quantum affne n-spaces Oq( n) can be obtained by iterated Ore extensions. Let n ≥1 and q be a matrix (qij)nxn whit entries in a field
n) can be obtained by iterated Ore extensions. Let n ≥1 and q be a matrix (qij)nxn whit entries in a field  where qii = 1y qijqji = 1 for all 1 ≤i, j ≤n. Then quantum affne n-space Oq(
where qii = 1y qijqji = 1 for all 1 ≤i, j ≤n. Then quantum affne n-space Oq( n) is defined to be
n) is defined to be  -algebra generated by x1, ···, xn with the relations xjxi = qijxixj for all 1 ≤i, j ≤n. The
-algebra generated by x1, ···, xn with the relations xjxi = qijxixj for all 1 ≤i, j ≤n. The  -algebra Oq(
-algebra Oq( n)isskew Calabi-Yau whit the Nakayama automorphism ν such that ν (xi) = (Πj=1 qji)xi (see [30], Proposition 4.1). This
n)isskew Calabi-Yau whit the Nakayama automorphism ν such that ν (xi) = (Πj=1 qji)xi (see [30], Proposition 4.1). This  -algebra is a skew PBW extension (see [29] ).
-algebra is a skew PBW extension (see [29] ).
The Jordan plane A =  ⟨x, y⟩/⟨yx -xy -x2⟩ is skew Calabi-Yau, but not Calabi-Yau (see [30]).
⟨x, y⟩/⟨yx -xy -x2⟩ is skew Calabi-Yau, but not Calabi-Yau (see [30]).
3.1.4. The universal enveloping algebra and the Sridharan enveloping algebra of Lie algebra
Let  be a finite dimensional Lie algebra over
be a finite dimensional Lie algebra over  with basis {x1, ···, xn}. The universal enveloping algebra of
with basis {x1, ···, xn}. The universal enveloping algebra of  , denoted
, denoted  (
( ), is a PBW extension of
), is a PBW extension of  since xir -rxi = 0, xixj -xjxi = [xi, xj] ∈
since xir -rxi = 0, xixj -xjxi = [xi, xj] ∈ =
=  +
+  x1 + ···+
x1 + ···+  xn, ri ∈
xn, ri ∈ , for 1 ≤i, j ≤n. Ji-Wei He, Fred Van Oystaeyen and Yinhuo Zhang showed that for the 3-dimensional Lie algebra
, for 1 ≤i, j ≤n. Ji-Wei He, Fred Van Oystaeyen and Yinhuo Zhang showed that for the 3-dimensional Lie algebra  with basis {x, y, z},
with basis {x, y, z},  (
( ) is a Calabi-Yau algebra if and only if the Lie bracket is given by [x, y] = ax + by + wz, [x, z] = cx + vy -bz,[y, z] = ux -cy + az, where a, b, c, u, v, w ∈
) is a Calabi-Yau algebra if and only if the Lie bracket is given by [x, y] = ax + by + wz, [x, z] = cx + vy -bz,[y, z] = ux -cy + az, where a, b, c, u, v, w ∈ ; and if
; and if  is a finite dimensional Lie algebra,
is a finite dimensional Lie algebra, 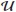 (
( ) is Calabi-Yau of dimension 3 if and only if
) is Calabi-Yau of dimension 3 if and only if  is isomorphic to one of the following Lie algebras (see [22], Proposition 4.5 and Proposition 4.6 ):
is isomorphic to one of the following Lie algebras (see [22], Proposition 4.5 and Proposition 4.6 ):
(i) The 3-dimensional simple Lie algebra sl(2,);
(ii)has a basis {x, y, z}such that [x, y] = y, [x, z] = -z and [y, z] = 0;
(iii) The Heisenberg algebra, that is;has a basis {x, y, z} such that [x, y] = z and [x, z] = [y, z] = 0;
(vi) The 3-dimensional abelian Lie algebra.
We note that if  is a finite dimensional Lie algebra over a field
is a finite dimensional Lie algebra over a field  and
and 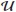 (
( ) is the universal enveloping algebra of
) is the universal enveloping algebra of  , then
, then 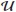 (
( ) is a skew PBW extension (see [16] ); in particular, universal enveloping Calabi-Yau algebra
) is a skew PBW extension (see [16] ); in particular, universal enveloping Calabi-Yau algebra 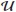 (
( ) of dimension 3 is a skew PBW extension.
) of dimension 3 is a skew PBW extension.
Let  be a finite dimensional Lie algebra, and let f ∈Z2(
be a finite dimensional Lie algebra, and let f ∈Z2( ,
,  ) be an arbitrary 2-cocycle, that is, f :
) be an arbitrary 2-cocycle, that is, f :  ×
× →
→ such that f (x, x) = 0 and
such that f (x, x) = 0 and
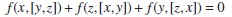
for all x, y, z ∈ .
.
The Sridharan enveloping algebra of  is defined to be the associative algebra
is defined to be the associative algebra 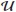 f (
f ( ) = T (
) = T ( )/I, where I is the two-side ideal of T (
)/I, where I is the two-side ideal of T ( ) generated by the elements
) generated by the elements
For x ∈ , we still denote by x its image in
, we still denote by x its image in  f(
f( ).
). 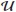 f(
f( ) is a filtered algebra with the associated graded algebra gr(
) is a filtered algebra with the associated graded algebra gr(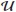 f(
f( )) being a polynomial algebra.
)) being a polynomial algebra.
Let  be a field and algebraically closed whit characteristic zero. If
be a field and algebraically closed whit characteristic zero. If  is a Lie K-algebra of dimension three then, the Sridharan enveloping algebra
is a Lie K-algebra of dimension three then, the Sridharan enveloping algebra 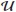 f(
f( ), for f ∈Z2(
), for f ∈Z2( ,
,  ), is isomorphic to one of ten following associative
), is isomorphic to one of ten following associative  -algebras, defined by three generator x, y, z and the following commutation relations (see [32], Theorem 1.3):
-algebras, defined by three generator x, y, z and the following commutation relations (see [32], Theorem 1.3):

where α ∈ -{0}. Therefore the Sridharan enveloping algebra
-{0}. Therefore the Sridharan enveloping algebra 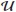 f(
f( )isaskew PBW extension.
)isaskew PBW extension.
Let  be a finite dimensional Lie algebra. Then for any 2-cocycle f ∈Z2(
be a finite dimensional Lie algebra. Then for any 2-cocycle f ∈Z2( ,
,  ), the following statements are equivalent (see [22], Theorem 5.3).
), the following statements are equivalent (see [22], Theorem 5.3).
(i) The Sridharan enveloping algebraf(
) is Calabi-Yau of dimension d.
(ii) The universal enveloping algebra(
) is Calabi-Yau of dimension d.
Let 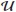 f(
f( ) be a Sridharan enveloping algebra of a finite dimensional Lie algebra
) be a Sridharan enveloping algebra of a finite dimensional Lie algebra  . Then
. Then 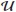 f(
f( ) is Calabi-Yau of dimension 3 if and only if
) is Calabi-Yau of dimension 3 if and only if 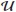 f(
f( ) is isomorphic to
) is isomorphic to  ⟨x,y,z⟩/⟨R⟩ with the commuting relations R listed in the following table (see [22], Theorem 5.5):
⟨x,y,z⟩/⟨R⟩ with the commuting relations R listed in the following table (see [22], Theorem 5.5):
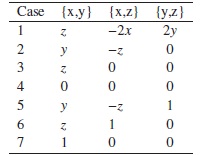
where {x,y}= xy -yx.
From the above discussion we have the following result.
Proposition 2. Let 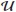 f(
f( ) be a Sridharan enveloping algebra of a finite dimensional Lie algebra
) be a Sridharan enveloping algebra of a finite dimensional Lie algebra  . If
. If 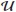 f(
f( ) is Calabi-Yau of dimension 3 then
) is Calabi-Yau of dimension 3 then 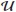 (
( ) is a skew PBW extension.
) is a skew PBW extension.
The Sridharan enveloping algebra of an n-dimensional abelian Lie algebra is n-Calabi-Yau; in particular the Weyl algebra An is 2n-Calabi-Yau (see [9], Theorem 6.5) as well as a skew PBW extension (see [16], Example 5).
3.2. Counterexamples
Next we will show some examples of algebras that are AS -regular, or N-Koszul, or Calabi-Yau, but are not skew PBW extensions.
-
A =
 ⟨x,y,z⟩/⟨xy-yx -z2 ,yz -z -x2 ,zx -xz - y2⟩ is AS -regular of global dimension 3 of type A (see [2], page 173). A is 2-Koszul (see [8], Proposition 5.2) and Calabi-Yau of dimension 3 (see [6], Proposition 5.4).
⟨x,y,z⟩/⟨xy-yx -z2 ,yz -z -x2 ,zx -xz - y2⟩ is AS -regular of global dimension 3 of type A (see [2], page 173). A is 2-Koszul (see [8], Proposition 5.2) and Calabi-Yau of dimension 3 (see [6], Proposition 5.4). -
A =
 ⟨x,y⟩/⟨x+ xy+ yx + yxy,xy + yx+ xyx + y3⟩ is AS -regular of global dimension 3 of type A (see [2], Theorem 3.10), A is 3Koszul (see [8], Proposition 5.2) and Calabi-Yau of dimension 3 (see [6], Proposition 5.4).
⟨x,y⟩/⟨x+ xy+ yx + yxy,xy + yx+ xyx + y3⟩ is AS -regular of global dimension 3 of type A (see [2], Theorem 3.10), A is 3Koszul (see [8], Proposition 5.2) and Calabi-Yau of dimension 3 (see [6], Proposition 5.4). -
A =
 ⟨x,y⟩/⟨yx⟩ is not AS -regular algebra. A is the only graded algebra of global dimension 2 and GK-dimension 2 which is not Noetherian (see [2], page 172). A is 2-Koszul (see [15], page 7), A is not 2-Calabi-Yau (see [6], Proposition 4.3)
⟨x,y⟩/⟨yx⟩ is not AS -regular algebra. A is the only graded algebra of global dimension 2 and GK-dimension 2 which is not Noetherian (see [2], page 172). A is 2-Koszul (see [15], page 7), A is not 2-Calabi-Yau (see [6], Proposition 4.3) -
The exterior algebra A = K⟨x1,···,xn⟩/⟨xk2,xixj + xjxi⟩k,i<j in n variables is an 2-Koszul algebra (see [31], Example 1.6).
-
If A =
 ⟨x1,···,xn⟩/I is an quadratic algebra and I is principal, then A is 2-Koszul (see [15], page 7). It depends on the ideal I whether A is Calabi-Yau or not.
⟨x1,···,xn⟩/I is an quadratic algebra and I is principal, then A is 2-Koszul (see [15], page 7). It depends on the ideal I whether A is Calabi-Yau or not. -
Consider V of dimension 1, V =
 x and w = xN+1. Then, dimR = dimRN+1 = 1, A(w)is N-Koszul (since the global dimension of A(w)is infinite, and A(w) is not 3-Calabi-Yau (see [4], Example 2.12).
x and w = xN+1. Then, dimR = dimRN+1 = 1, A(w)is N-Koszul (since the global dimension of A(w)is infinite, and A(w) is not 3-Calabi-Yau (see [4], Example 2.12).
4. Some Properties Preserved by Ore Extensions
Suppose σ : A → A is a graded algebra automorphism and δ : A(-1) → A is a graded σ-derivation. If B := A[z;σ,δ] is the associated Ore extension, then B isaskew PBW extension. In this case we have B = A[z,σ; δ] = σ(A)⟨x⟩ (see [16], Example 5).
Below we list some properties that are preserved by Ore extensions:
-
If A is a connected graded algebra then B is a connected graded algebra.
-
If A is homologically smooth, then so is B (see [30], Proposition 3.1).
-
B is 2-Koszul if and only if A is 2-Koszul (see [33], Corollary 1.3).
-
Let A =
 ⟨x1,...,xn⟩/⟨f⟩ where f = (x1,..., xn)M(x1,···,xn)t and M is an n × n matrix. Then A is Calabi-Yau of dimension 2 if and only if M is invertible and anti-symmetric (see [24], Corollary 1).
⟨x1,...,xn⟩/⟨f⟩ where f = (x1,..., xn)M(x1,···,xn)t and M is an n × n matrix. Then A is Calabi-Yau of dimension 2 if and only if M is invertible and anti-symmetric (see [24], Corollary 1).
Let δ be a graded derivation of the free algebra ⟨x1,...,xn⟩ of degree 1. If δ( f ) = 0, then δ induces a graded derivation
⟨x1,...,xn⟩ of degree 1. If δ( f ) = 0, then δ induces a graded derivation 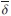 on A. Let B = A[z;
on A. Let B = A[z; 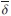 ] be the Ore extension of A defined by the graded derivation
] be the Ore extension of A defined by the graded derivation 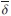 . Then B is a graded Calabi-Yau algebra of dimension 3 (see [21], Proposition 1.3).
. Then B is a graded Calabi-Yau algebra of dimension 3 (see [21], Proposition 1.3). -
If A is ν -skew Calabi-Yau projective
 -algebra of dimension d, then B is skew Calabi-Yau of dimension d + 1 and the Nakayama automorphism ν' of B satisfies that ν' = σ-1ν and |A ν' (z) = uz+ b, with u,b ∈ A and u invertible (see [30], Theorem 3.3).
-algebra of dimension d, then B is skew Calabi-Yau of dimension d + 1 and the Nakayama automorphism ν' of B satisfies that ν' = σ-1ν and |A ν' (z) = uz+ b, with u,b ∈ A and u invertible (see [30], Theorem 3.3). -
Let A be a 2-Koszul AS -regular algebra of global dimension d with the Nakayama automorphism ξ. Then B = A[z,ξ] is a Calabi-Yau algebra of dimension d + 1 (see [25], Theorem 3.3).
-
Let A be a ν-skew Calabi-Yau algebra of dimension d and σ ∈ Aut(A), then A[x;σ] and A[x±1;σ] are Calabi-Yau algebras of dimension d + 1 (see [18], Theorema 1.1). Furthermore, if A[x; σ] is Calabi-Yau, then A[x±1; σ] is Calabi-Yau.
-
Now we present an example of skew Calabi-Yau algebra that is not Calabi-Yau (see [30] ), and then, we consider the corresponding Ore extension. Let A =
 ⟨x,y⟩/⟨yx - xy- x2⟩ be the Jordan plane, A is AS -regular algebra of dimension 2 and therefore A is 2-Koszul, A =
⟨x,y⟩/⟨yx - xy- x2⟩ be the Jordan plane, A is AS -regular algebra of dimension 2 and therefore A is 2-Koszul, A =  [x] [y,δ1] with δ1(x) = x2. It follows that A is skew Calabi-Yau but not Calabi-Yau. A has Nakayama automorphism given by ν (x) = x and ν (y) = 2x + y, B = A[z;ν] is an Ore extension of Jordan plane. Then B is skew Calabi-Yau with the Nakayama automorphism ν' such that ν' (x) = x and ν' (y) = y. B =
[x] [y,δ1] with δ1(x) = x2. It follows that A is skew Calabi-Yau but not Calabi-Yau. A has Nakayama automorphism given by ν (x) = x and ν (y) = 2x + y, B = A[z;ν] is an Ore extension of Jordan plane. Then B is skew Calabi-Yau with the Nakayama automorphism ν' such that ν' (x) = x and ν' (y) = y. B =  [x,z] [y; δ] where δ is given by δ(x) = x2 and δ(z) = -2xz. So, ν' (z) = z. It follows that B is Calabi-Yau, which was already proved by Berger and Pichereau in [5].
[x,z] [y; δ] where δ is given by δ(x) = x2 and δ(z) = -2xz. So, ν' (z) = z. It follows that B is Calabi-Yau, which was already proved by Berger and Pichereau in [5]. -
In [44], AS -regular algebras of dimension 5 generated by two generators of degree 1 with three generating relations of degree 4 are classified under some generic condition. There are nine types such AS -regular algebras in this classification list. Among them, the algebras D and G are given by iterated Ore extensions (see [44], Section 5.2).
The algebra D is skew Calabi-Yau with the Nakayama automorphism ν given by ν(x) = p-3q4x; ν (y) = p3q-4y. D is Calabi-Yau if and only if that p,q satisfy the system of equations (see [30], Theorem 4.3)
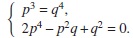
The algebra G is skew Calabi-Yau with the Nakayama automorphism ν given by ν (x) = gx; ν (y) = g-1y. D is Calabi-Yau if and only if g = 1.
They study and classification of AS -regular algebras of dimension five with two generators under an additional Z2-grading uses Gröbner basis computations (see [48]).
-
Let
 be a field, let n be an even natural number ≥ 2, and let A be the associative
be a field, let n be an even natural number ≥ 2, and let A be the associative  -algebra defined by generators x1,...,xn subject to the single relation
-algebra defined by generators x1,...,xn subject to the single relation
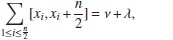
where the bracket stands for the commutator, ν is a linear combination of the xi's, and λ ∈  . Then the filtered algebra A is 2-Koszul. Furthermore A is 2-Calabi-Yau if and only if ν = 0 (see [9], Theorem 6.4). So, if σ2 = i
. Then the filtered algebra A is 2-Koszul. Furthermore A is 2-Calabi-Yau if and only if ν = 0 (see [9], Theorem 6.4). So, if σ2 = i [x1] and δ2(
[x1] and δ2( [x1] ) ⊆
[x1] ) ⊆  , then the skew PBW extension σ(
, then the skew PBW extension σ( )⟨x1,x2⟩ ℝ
)⟨x1,x2⟩ ℝ  [x1] [x2; σ2,δ2]is 2-Calabi-Yau.
[x1] [x2; σ2,δ2]is 2-Calabi-Yau.
References
[1] J. P. Acosta, C. Chaparro, O. Lezama, I. Ojeda and C. Venegas, "Ore and Goldie theorems for skew PBW extensions", Asian-European J. Math., vol. 6 (4), pp. 1350061-1 -1350061-20, 2013. [ Links ]
[2] M. Artin and W. F. Schelter, "Graded algebras of global dimension 3", Adv. Math., vol. 66, pp. 171-216, 1987. [ Links ]
[3] R. Berger, "Koszulity for nonquadratic algebras", J. Algebra, vol. 239, pp. 705-734, 2001. [ Links ]
[4] R. Berger and A. Solotar, "A criterion for homogeneous potencials to be 3-Calabi-Yau", arXiv:1203.3029, 2013. [ Links ]
[5] R. Berger and A. Pichereau, "Calabi-Yau algebras viewed as deformations of Poisson algebras", Algebr. Represent. Theory, vol. 17 (3), pp. 735-773, 2014. [ Links ]
[6] R. Berger and R. Taillefer, "Poincare-Birkhoff-Witt deformations of Calabi-Yau algebras", J. Noncommut. Geom., vol. 1, pp. 241-270, 2007. [ Links ]
[7] R. Berger and V. Ginzburg, "Higher Symplectic Reflection Algebras and Non-homogeneous N-Koszul Property", J. Algebra, vol 304, pp. 577601, 2006. [ Links ]
[8] R. Berger and N. Marconnet, "Koszul and Gorenstein properties for homogeneous algebras", Algebr. Represent. Theory, vol. 1, pp. 67-97, 2006. [ Links ]
[9] R. Berger, "Gerasimov's theorem and N-Koszul algebras", J. London Math. Soc., vol. 79, pp. 631-648, 2009. [ Links ]
[10] R. Bocklandt, "Graded Calabi Yau algebras of dimension 3 (with an appendix by M. Van den Bergh)", J. Pure Appl. Algebra, vol. 212, pp. 14-32, 2008. [ Links ]
[11] R. Bocklandt, "Calabi Yau algebras and weighted quiver polyhedra", Math. Z., vol. 273, pp. 311-329, 2013. [ Links ]
[12] K. A. Brown, I. G. Gordon and C. H. Stroppel, "Cherednik, Hecke and quantum algebras as free Frobenius and Calabi-Yau extensions", J. Algebra, vol. 319 (3), pp. 1007-1034, 2008. [ Links ]
[13] T. Cassidy and B. Shelton, "Generalizing the notion of Koszul algebra", Math. Z., vol. 260, pp. 93-114, 2008. [ Links ]
[14] G. Floystad and J. E. Vatne, "PBW-Deformations of N-Koszul Algebras", J. Algebra, vol. 302, pp. 116-155, 2006. [ Links ]
[15] R. Fröberg, "Koszul Algebras", Matematiska institutionen Stockholms Universitet 10691 Stockholm Sweden, 1998. [ Links ]
[16] C. Gallego and O. Lezama, "Gröbner bases for ideals of σ - PBW extensions", Comm. Algebra, vol. 39, pp. 1-26, 2011. [ Links ]
[17] V. Ginzburg, "Calabi-Yau algebras", arXiv:math.AG/0612139v3, 2006. [ Links ]
[18] J. Goodman, and U. Krähmer, "Untwisting a twisted Calabi-Yau Algebra", J. Algebra, vol. 406, pp. 271-289, 2014. [ Links ]
[19] E. L. Green and E. Marcos, "d-Koszul algebras, 2-d determined algebras and 2-d-Koszul algebras", J. Pure Appl. Algebra, vol. 215 (4), pp. 439-449, 2011. [ Links ]
[20] E. L. Green, E. Marcos, R. Martínez-Villa and Zhang, "D-Koszul algebras", J. Pure Appl. Algebra, vol. 193 (1-3), pp. 141-162, 2004. [ Links ]
[21] J. W. He, F. Van Oystaeyen and Y. Zhang, "Graded 3-Calabi-Yau Algebras as Ore Extensions of 2-Calabi-Yau Algebras", arXiv:1303.5293v1, 2013. [ Links ]
[22] J. W. He, F. Van Oystaeyen and Y. Zhang, "Cocommutative Calabi-Yau Hopf Algebras and Deformations", J. Algebra, vol. 324, pp. 1921-1939, 2010. [ Links ]
[23] J. W. He, F. Van Oystaeyen and Y. Zhang, "Hopf algebra actions on differential graded algebras and applications", Bull. Belg. Math. Soc. Simon Stevin, vol. 18, pp. 99-111, 2011. [ Links ]
[24] J. W. He, F. Van Oystaeyen and Y. Zhang, "Calabi-Yau algebras and their deformations", Bull. Math. Soc. Sci. Math. Roumanie, Tome 56 (104), no. 3, pp. 335-347, 2013. [ Links ]
[25] J. W. He, F. Van Oystaeyen and Y. Zhang, "Skew polynomial algebras with coeficients in Koszul Artin-Schelter regular algebras", J. Algebra, vol. 390, pp. 231-249, 2013. [ Links ]
[26] J. W. He, F. Van Oystaeyen and Y. Zhang, "Deformations of Koszul Artin-Schelter Gorenstein algebras", Manuscripta Math., Doi: 10.1007/s00229-012-0580-z, 2012. [ Links ]
[27] O. Iyama, I. Reiten, "Fomin-Zelevinsky mutation and tilting modules over Calabi-Yau algebras", Am. J. Math., vol. 130, pp. 1087-1149, 2008. [ Links ]
[28] P. Le Meur, "Crossed productd of Calabi-Yau algebras by finite groups", arXiv:1006.1082, 2010. [ Links ]
[29] O. Lezama and A. Reyes, "Some Homological Properties of Skew PBW Extensions", Comm. Algebra, vol. 42, pp. 1200-1230, 2014. [ Links ]
[30] L. -Y. Liu, S. Wan and Q. -S Wu, "Twisted Calabi-Yau property of Ore extensions", J. Noncommut. Geom., vol. 8 (2), pp. 587-609, 2014. [ Links ]
[31] R. Martínez-Villa, "Introduction to Koszul Algebras", Rev. Un. Mat. Argentina, vol. 48 (2), pp. 67-95, 2007. [ Links ]
[32] P. Nuss, "L'homologie cyclique des algèbres enveloppantes des algèbres de Lie de dimension trois", J. Pure Appl. Algebra, vol. 73, pp. 39-71, 1991. [ Links ]
[33] C. Phan, "The Yoneda algebra of a graded Ore extension", Comm. Algebra, vol. 40, pp. 834-844, 2012. [ Links ]
[34] S. Priddy, "Koszul Resolutions", Trans. Amer. Math. Soc., vol. 152, pp. 39-60, 1970. [ Links ]
[35] A. Reyes, "Uniform Dimension over Skew PBW Extensions", Rev. Colombiana Mat., vol. 48, pp. 79-96, 2014. [ Links ]
[36] A. Reyes, "Gelfand-Kirillov Dimension of Skew PBW Extensions", Rev. Colombiana Mat., vol. 47 (1), pp. 95-111, 2013. [ Links ]
[37] M. Reyes, D. Rogalski and J. Zang, "Skew Calabi-Yau Algebras and Homological Identities", arXiv:1302.0437v2 [math.RA], 2013. [ Links ]
[38] B. Shelton and C. Tingey, "On Koszul algebras and a new construction of Artin-Schelter regular algebras", J. Algebra, vol. 241 (2), pp. 789-798, 2001. [ Links ]
[39] S. P. Smith, "A 3-Calabi-Yau algebra with G2 symetry constructed from the octonions", arXiv:1104.3824v1, 2011. [ Links ]
[40] D. R. Stephenson and J.J. Zhang, "Growth of graded Noetherian rings", Proc. Amer. Math. Soc., vol. 125, pp. 1593-1605, 1997. [ Links ]
[41] M. Suárez-Alvarez, "Untwisting algebras with van den Bergh duality into Calabi-Yau algebras", arXiv:1311.3339v1, 2013. [ Links ]
[42] M. Van den Bergh, "Introduction to Super Potentials (informal evening talk)", Oberwolfach Report 6, 2005. [ Links ]
[43] M. Van den Bergh, "Calabi-Yau algebras and superpotentials", Sel.Math.New Ser DOI 10.1007/s00029-014-0166-6, 2014. [ Links ]
[44] S. -Q Wang and Q. -S Wu, "A class of AS-regular algebras of dimension five", J. Algebra, vol. 362, pp. 117-144, 2012. [ Links ]
[45] Q. -S. Wu and C. Zhu, "Skew group algebras of Calabi-Yau algebras", J. Algebra, vol. 340, pp. 53-76, 2011. [ Links ]
[46] Q. -S. Wu and C. Zhu, "Poincaré-Birkhoff-Witt Deformation of Koszul Calabi-Yau Algebras", Algebr. Represent. Theory, vol. 16, pp. 405-420, 2013. [ Links ]
[47] X. Yu and Y. Zhang, "Calabi-Yau pointed Hopf algebras of finite Cartan type", J. Noncommut. Geom., vol. 7 (4), pp. 1105-1144, 2013. [ Links ]
[48] G. -S. Zhou and D. -M Lu, "Artin-Schelter regular algebras of dimension five with two generators", J. Pure Appl. Algebra, vol. 218, pp. 937-961, 2014. [ Links ]
[49] C. Zhu, F. Van Oystaeyen and Y. Zhang, "Calabi-Yau extensions and localization of Koszul regular algebras", arXiv:1401.0330v1, 2014. [ Links ]













