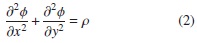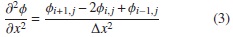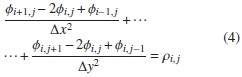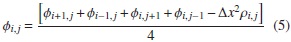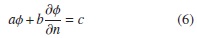Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia en Desarrollo
Print version ISSN 0121-7488
Ciencia en Desarrollo vol.6 no.2 Tunja July/Dec. 2015
Discretización en diferencias finitas de la ecuación de Laplace y Poisson. Aplicación a un anillo circular (dona)
Finite Difference Discretization of the Laplace and Poisson Equations. Application to the Anular Ring (donut)
L. M. Méndez Morenoa,*
G. Orozco Hernándezb
F. Fonsecab
a Departamento de Ingeniería Mecánica y Mecatrónicas Universidad Nacional de Colombia, sede Bogotá, Colombia.
b Universidad Nacional de Colombia, Departamento de Física, sede Bogotá, Colombia
* Autor de correspondencia: lmmendezm@unal.edu.co
Recepción: 05-ene-15 Aceptación: 24-jun-15
Resumen
Entre los métodos de solución numérica más comunes para ecuaciones diferenciales parciales (EDP) se encuentran el método de las diferencias finitas y el método de los elementos finitos, que se acercan a la solución real a través de un algoritmo de convergencia de manera eficiente y acertada. Muchos de los fenómenos físicos que se pueden estudiar mediante estas técnicas obedecen su comportamiento a las EDP's de Laplace y de Poisson, sobre las que se pueden restringir diferentes condiciones iniciales y de frontera, para limitar las soluciones de la ecuación. Este trabajo muestra la aplicación del método de diferencias finitas con un manejo sencillo de la discretización del dominio y, así mismo, un manejo sencillo de las condiciones de frontera sobre varios dominios, principalmente sobre dominios del tipo anillo o "dona", mostrando resultados interesantes al seleccionar condiciones de frontera del tipo Dirichlet.
Palabras clave: diferencias finitas, dona, Laplace, Poisson.
Abstract
Among the more common numeric methods of solution for partial differential equations (PDE) we have the finite differences method and the finite elements method that approach the real solution through an effcient and accurate algorithm of convergence. Many of the physical phenomena that can be studied by means of these techniques obey their behavior to the EDP' s of Laplace and Poisson, on whom different initial and/or boundary conditions can be restricted, to limit the solutions of the equation. This work shows the application of the finite difference method with a simple handling of the domain discretization and a simple handling of the boundary conditions on several domains, mainly with the domain with shape of ring or "donut", showing interesting results when selecting border conditions of the Dirichlet kind.
Key words: Differences finitas, Dona, Laplace, Poisson.
1 Introducción
Cuando se quiere enseñar métodos numéricos para la solución de ecuaciones diferenciales parciales (EDP) en las áreas de matemáticas, física e ingeniería, existe una tendencia común a resolver problemas sobre dominios simétricos con condiciones de frontera del tipo Dirichlet y Neumann. Las EDP sobre las cuales se trabaja normalmente son la ecuación de Laplace y la ecuación de Poisson, las cuales aparecen en áreas de la ciencia como la electricidad, conducción de calor y flujo de fluídos, por lo que resolverlas a través de métodos numéricos reviste un interés importante. Los métodos numéricos más comunes para la solución de estas EDP son el método de diferencias finitas y el método de elementos finitos, aplicados sobre dominios rectangulares [1, 6] o circulares [1].
Este trabajo está dirigido a implementar el método de diferencias finitas para la solución de la ecuación de Laplace sobre un dominio en forma de anillo circular o "dona", que representa un reto adicional y que permite mostrar una técnica del manejo de la frontera y sus condiciones.
2 Modelamiento matemático
El modelamiento matemático de la ecuación de La-place comienza con plantear la ecuación general de Poisson, que es la ecuación 1, para proceder a utilizar la técnica de diferencias finitas que permite transformar las derivadas parciales en diferencias entre puntos discretos del dominio. Para esto proyectamos resolver un problema que en el dominio espacial es tridimensional (3D), pero que por facilidad del trabajo lo haremos bidimensional (2D). Partiendo de esto, la ecuación de Poisson (ecuación 1) se transforma en la ecuación 2.
Para aplicar el método de diferencias finitas procedemos a discretizar el dominio en sus dos dimensiones x e y, lo cual, a su vez, discretiza el campo φ de la ecuación diferencial. Es por esto que ahora las derivadas observadas en la ecuación diferencial 2 se transforman en las que se observan en la ecuación 3. Estas diferencias son el resultado de la expansión en series de Taylor de los términos de la ecuación 2 y de suponer una exactitud de segundo orden despreciable, con lo cual se obtienen las ecuaciones diferenciales en la forma de ecuaciones de diferencias que ya mencionamos y donde el dominio se ha transformado en un número finito de puntos [1, 5].
Si reemplazamos esto en la ecuación diferencial 2, tenemos la ecuación 4, que refleja el problema ya habiendo discretizado el dominio.
Utilizando esta ecuación 4, despejamos φi, j, y suponiendo que Δx =Δy obtenemos la ecuación 5 [5, 6].
Si ρi, j es igual a cero, significa que el sistema ya está discretizado y listo para resolver la ecuación de Laplace [1, 6].
Para poder resolver esta ecuación diferencial faltaría agregar condiciones de frontera. Para esto utilizamos la ecuación 6, de la cual podemos establecer condiciones de frontera así: cuando en la frontera del dominio, (la cual se relaciona de alguna manera conocida con la numeración de nodos i y j), se tiene alguna condición conocida de la variable (Dirichlet b =0), de su primera derivada (Newman a =0) o de una combinación lineal de estas dos (Robin c =0), según se plantearon los coeficientes de la ecuación 6.
De la ecuación 5 se puede entender que la forma de cálculo se realiza fácilmente sobre un dominio rectangular, donde el recorrido de los nodos i y j es consecutivo, resultando en una complicación cuando el dominio es diferente a un rectángulo. Para no modificar ni el dominio general, ni el algoritmo presentado, proponemos la realización de un manejo de nodos. Este manejo requiere que el dominio quede en el interior del rectángulo utilizado, que seguirá siendo la geometría base y donde se ubicarán los no-dos de la discretización, pero para realizar el cálculo que establece la ecuación 5, solamente se realizará en los nodos que se consideren internos del dominio de interés.
Para establecer si un nodo es interno o no, solo se fija en un archivo de nodos qué característica tiene entre: interno, externo o frontera, se puede almacenar hasta de qué parte de la frontera es el nodo, con una codificación numérica, como se hizo en este trabajo. Como es posible que los puntos de la frontera no coincidan con los nodos de la discretización del dominio, se deberá realizar un manejo de error máximo permitido en la distancia de un nodo a la frontera, para que ese nodo pertenezca a la frontera. Con este método, se puede seguir utilizando el algoritmo de cálculo propuesto en la referencia [5, 6] y extenderlo a cualquier dominio.
3 Resultados
Utilizando el algoritmo derivado del modelo matemático explicado en la sección anterior y soportado en diferentes trabajos donde se puede consultar [1, 2, 3, 4, 5, 6, 7, 8], se obtienen los siguientes resultados para geometrías que han sido presentadas en la literatura al respecto y en las referencias consultadas. En la figura 1 podemos observar los casos de aplicación de esta técnica sobre un dominio circular con condiciones de frontera del tipo Dirichlet por facilidad de trabajo y sobre un dominio en forma de L, con condiciones de frontera tipo Dirichlet y Neumann, para mostrar la versatilidad del algoritmo de trabajo fronterizo. Aunque el algoritmo permite trabajar con la ecuación de Poisson, se ha fijado del valor de ρ en cero, durante la ejecución del algoritmo, por facilidad de entendimiento, y por lo tanto se trabaja con la ecuación de Laplace.
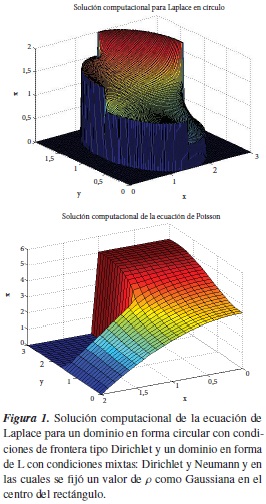
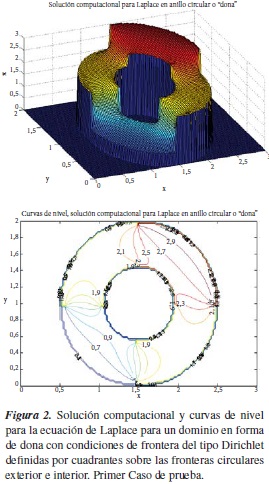
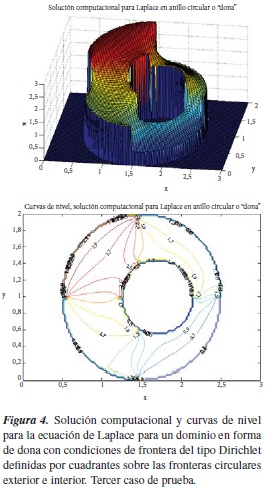
Este algoritmo también se aplicó sobre un dominio en forma de dona o de anillo, el cual permite definir el radio y la excentricidad del circulo interior; en este dominio se implementaron condiciones de frontera del tipo Dirichlet, por cuadrantes, como se puede observar en las figuras 2, 3 y 4. De estas figuras se puede observar la versatilidad del algoritmo y el trabajo sobre geometrías que no son perfectamente simétricas, al especificar cierta excentricidad de la frontera circular interior.
En la figura 2 podemos observar el caso de la frontera circular interior centrada, en la figura 3 podemos observar el caso de la frontera circular interior des-centrada en x e y y en la figura 4 podemos observar el caso de la frontera circular interior descentrada en x.
4 Conclusiones
Después de observar la presentación de los resultados obtenidos, quedan muchas buenas razones para utilizar el método de diferencias finitas en la solución de ecuaciones diferenciales en derivadas parciales (EDP) que representen fenómenos físicos de la realidad. Si observamos bien, podríamos decir que manejando adecuadamente los coeficientes de la EDP según la realidad que se procura modelar, podríamos simular perfiles de potencial en conductores con geometrías como las que simulamos. Por ejemplo, la simulación de la dona podría representar el perfil de temperatura en la sección transversal del aislamiento de un tubo que conduzca un fluido caliente; el problema con geometría rectangular podría representar el potencial al colocar una fuente de campo en el centro de un lugar cerrado, ejemplo un ducto de ventilación con una resistencia calefactora en el centro del mismo. La geometría en forma de L puede ser una placa conductora de temperatura o un ducto de ventilación con condiciones térmicas de aislamiento. En fin, sinnúmero de problemas reales pueden ser simulados a través de las técnicas utilizadas en los programas desarrollados.
Durante este trabajo nos enfrentamos a la necesidad de simular condiciones de frontera de diferentes tipos; ya que se procedió en general con condiciones de tipo Dirichlet, simulamos el caso más sencillo de frontera Neumann, que es el de gradiente cero en algunas fronteras del dominio en forma de L. Se puede evidenciar un futuro trabajo que consista en el hecho de que las fronteras tipo Dirichlet no fueran constantes, sino una función, para ganar en realismo y poder simular condiciones reales.
Para finalizar, el manejo geométrico utilizado en la identificación de nodos internos y externos, así como de nodos frontera, fue interesante, sencillo y fácil de implementar, dejando abierta la posibilidad de realizar los cálculos sobre cualquier tipo de dominio.
Referencias
[1] M. Gonzáles Vásquez, "Simulaciones numéricas de la ecuación de calor: diferencias finitas", tesis para obtener el título de Licenciado en Matemáticas, Universidad Veracruzana, Junio 2007. [ Links ]
[2] M. Elliotis, G. Georgiou y C. Xenophontos, "The solution of Laplacian problems over Lshaped domains with a singular function boundary integral method", Communications in numerical methods in engineering, no. 18, pp. 213-222, 2002. [ Links ]
[3] A. Jaun, "Numerical methods for partial differential equations", Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland. Chalmers Institute of Technology, Göteborg, Sweden. Royal Institute of Technology, Stockholm, Sweden. Tomado de: http://pde.fusion.kth.se, September 10, 2001. [ Links ]
[4] J. J. Ramírez R., C. A. Vanegas G. y A. M. Vi-llegas R., "Método de diferencias finitas para la solución de ecuaciones en derivadas parciales", Universidad EAFIT, Medellín, Colombia. [ Links ]
[5] A. K. Mitra, "Finite difference method for the solution of Laplace equation", Department of aerospace engineering Iowa state University. [ Links ]
[6] M. Sen, "Notes on finnite-difference methods for AME301: differential equations, vibrations and controls", Department of aerospace and mechanical engineering, University of Notre Dame, IN 46556, U.S.A., 2005. [ Links ]
[7] H. A. Escorcia, L. M. Villada, M. Toro y C. E. Mejía, "Uso de un software como propuesta metodológica para la enseñanza de ecauciones diferenciales", Universidad Nacional de Colombia, Medellín. Sociedad Colombiana de matemáticas. XV Congreso Nacional de Matemáticas. [ Links ]
[8] J. W. Duncan, "The accuracy of finite-difference solutions of Laplace's equation", IEEE Transactions on microwave theory and techniques, MTT-15, 1997. [ Links ]





![Volumetric Properties of Ethanol and [Emim]+ [CF3SO3]- Aqueous Solutions from Refraction Index Data](/img/en/next.gif)