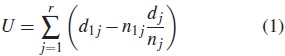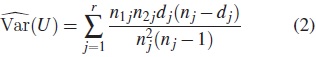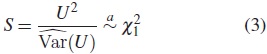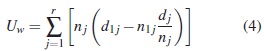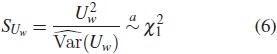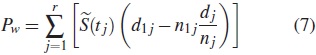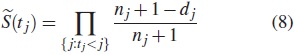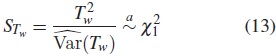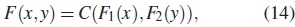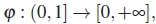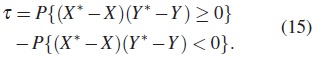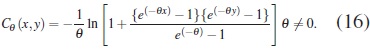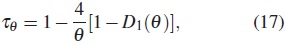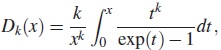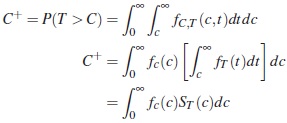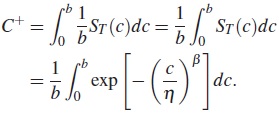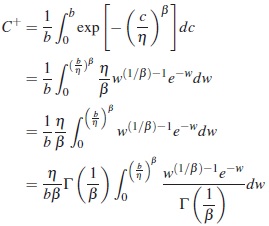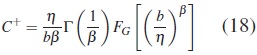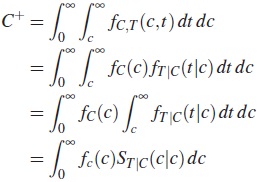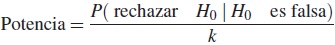Efecto de la censura informativa sobre la potencia de algunas pruebas tipo Log-Rank

Effect of Informative Censoring on the Power of Some Log-Rank Type Tests

L. P. Brun González^a,*
J. C. Salazar Uribe^a

^a Escuela de Estadística, Universidad Nacional de Colombia, Sede Medellín, Colombia.
^* Autor de correspondencia: lorenapbrun@gmail.com.

Recepción: 18-sep-2015 Aceptación: 20-dic-2015

Resumen

El análisis de supervivencia consiste en un conjunto de técnicas para analizar el tiempo de seguimiento hasta la ocurrencia de un evento de interés, también denominado tiempo de vida, el cual se observa completa o parcialmente. En la práctica, un problema frecuente consiste en comparar las experiencias de supervivencia de al menos dos grupos bajo estudio. La estrategia de análisis más común consiste en usar pruebas Log-Rank, pero estas no distinguen si el mecanismo de censura es informativo o no. En este trabajo se evaluó, bajo diferentes escenarios de simulación, la potencia estimada de algunas pruebas Log-Rank cuando los datos presentan censura informativa. Se encontró evidencia de un mejor desempeño de la prueba de Wilcoxon.

Palabras clave: análisis de supervivencia, censura informativa, tiempo de falla, pruebas Log-Rank, potencia de la prueba.

Abstract

The survival analysis is a set of techniques for analyzing the elapsed time until the occurrence of an event of interest, also called lifetime, which can be completely or partially observed. In practice, a common problem is to compare the survival experiences of at least two groups under study. The analysis strategy most common is to use Log-Rank tests, but these do not distinguish whether the mechanism of censoring it is informative or not. In this work it was evaluated, under different simulation scenarios, the estimated power of some Log-Rank tests when informative censoring is presented. We found evidence favoring the Wilcoxon test.

Key words: Failure Time, Informative, Log-Rank Tests Censoring, Survival Analysis, Power of a Test.

1. Introducción

En diversos estudios, el interés consiste en observar el tiempo que transcurre desde un evento inicial que determina la inclusión de un individuo en el estudio, y un evento final que, generalmente, se denomina falla. Una característica del análisis de supervivencia es la censura. La duración de un evento está censurada cuando su tiempo de falla no ha sido observado dentro del periodo de estudio, [1].

Entre los métodos para analizar este tipo de datos se encuentran las pruebas Log-Rank, que comparan dos o más curvas de supervivencia bajo la hipótesis nula de que estas son iguales [2]; estas funcionan bien cuando se trabaja con censura no informativa [3], que ocurre cuando el tiempo de falla y los tiempos censurados son independientes.

El objetivo central de este trabajo fue evaluar estadísticamente cómo se comportan algunas pruebas tipo Log-Rank cuando la censura es informativa, y presentar algunos escenarios donde incluso al ignorar la dependencia entre las fallas y la censura, la potencia estimada de las pruebas Log-Rank se mantiene. Demasiada censura informativa puede conducir a sesgos grandes en el proceso de estimación de los parámetros del modelo [1].

En este trabajo se presenta un estudio de simulación en el cual se evidencian los porcentajes de censura para los que las pruebas Log-Rank tienen una alta y baja potencia estimada, teniendo en cuenta el tamaño muestral y si la censura es informativa o no.

2. Definiciones y pruebas Log-Rank

2.1. Censura

La censura ocurre cuando el tiempo exacto de un evento no ha sido observado para algunos individuos, [4]. Para las observaciones censuradas solo se conoce el límite inferior y el límite superior del tiempo del evento. La manera como se recogen los datos determina las propiedades de los mecanismos de censura, que son: censura tipo I, en la cual los individuos son observados hasta un tiempo determinado, es decir, los individuos son monitoreados por un periodo de tiempo t.

2.2. Censura aleatoria

La censura tipo II, en la cual los individuos son observados hasta que ocurra un número determinado de fallas o eventos de interés; esto es, al inicio del estudio se decidió observar hasta registrar r fallas, en la cual hay dependencia del tamaño de muestra (denotado por n) y las fallas que se observen. Aquí, todos los individuos son puestos en estudio al mismo tiempo y se da el término de este cuando r de los n individuos han presentado el evento de interés, donde r es un número entero positivo determinado previamente por el investigador, y es tal que r < n.

2.3. Censura a derecha

Se presenta cuando a la última observación que se le hace al individuo no ha ocurrido el evento que se desea observar.

2.4. Censura informativa

La censura puede ser no informativa o informativa. Técnicamente, la censura se considera no informativa cuando las variables aleatorias asociadas a los tiempos de falla y de censura son independientes, y se considera informativa cuando las variables aleatorias asociadas a los tiempos de falla y censura no son independientes. Para ilustrar la censura informativa, considere, por ejemplo, una cohorte de pacientes que están en un grupo de tratamiento. Suponga, además, que algunos de estos sujetos se retiran del estudio antes de que termine, debido a que están experimentando efectos secundarios adversos que comprometen o deterioran su condición física. Esto significa que la censura está relacionada con algún factor asociado con el tiempo de supervivencia actual.

2.5. Pruebas Log-Rank

En la literatura se encuentran varias alternativas a la prueba de Log-Rank diseñadas para probar la hipótesis de que dos o más curvas de supervivencia son equivalentes [1, 6, 7, 8].

Se describirá la prueba Log-Rank para cuando se quieren comparar estadísticamente dos curvas de supervivencia. La prueba Log-Rank, también conocida como la prueba de Mantel-Haenszel, descrita por [5], es una prueba que se distribuye asintóticamente como una chi-cuadrado y que usa como criterio de prueba un estadístico que proporciona una comparación general de las curvas de supervivencia, es decir, para todo tiempo t. Utiliza el valor observado contra el valor esperado y no las categorías de los resultados, es decir, equivale a la diferencia entre el número de fallas observadas en cada grupo y su correspondiente número esperado de fallas bajo la hipótesis nula. Específicamente, sean t₁ < t₂ < ···< tr los tiempos de falla ordenados y

d_ij : el número de fallas en el grupo i hasta el tiempo t_j, i = 1,2

n_ij : Número de individuos bajo observación y a riesgo del grupo ial tiempo t_j , i=1,2

Entonces d_j = d_{1 j} +d_{2 j} representa el número de fallas en ambos grupos y n_j el número de unidades bajo observación y n_j = n_{1 j} +n_{2 j} el número de individuos a riesgo en ambos grupos al tiempo t_j.

Si la supervivencia es la misma en ambos grupos, entonces el número esperado de fallas en el grupo 1 al tiempo t_j es e_{1 j} = n_{1 j}d_j/n_j. La prueba está basada en la diferencia entre las fallas observadas y las fallas esperadas,

La varianza para U puede estimarse como

El estadístico para la prueba long-rank está dado por

2.6. Prueba de Wilcoxon

Esta prueba se basa en la suma ponderada de las diferencias observadas y esperadas entre los números de fallas usando como peso o ponderación a n_j. El estadístico de prueba se construye usando 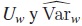, que están dadas respectivamente por:

La varianza puede estimarse como

Así, el estadístico para la prueba de Wilcoxon está dado por:

Al utilizar el número de individuos en riesgo como la ponderación, la prueba de Wilcoxon da un mayor peso a la primera parte de la curva, donde el tamaño de la muestra es mayor que en los puntos de tiempo posteriores, cuando solo pocos individuos permanecen bajo observación y a riesgo, [6].

2.7. Prueba de Peto y Peto

En la prueba de Peto y Peto, los pesos son el tiempo de interrupción de la j-ésima estimación de la supervivencia 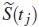calculado sobre todos los grupos combinados. Esta estimación de la supervivencia 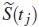es similar a la estimación de la curva de supervivencia de Kaplan-Meier. El estadístico de prueba está especificado como:

La varianza puede estimarse usando esta expresión:

Por lo tanto, el estadístico para la prueba de Peto está dado por:

Esta prueba también da más peso a la información que se encuentra al comienzo de la curva de supervivencia, donde el número de individuos bajo observación y a riesgo es mayor [7].

2.8. Prueba de Tarone-Ware

El estadístico de prueba propuesto por [8] aplica más peso a los primeros tiempos de falla, y la ponderación de los individuos es el tiempo observado menos el tiempo esperado en t_j y está dada por la raíz cuadrada del número de individuos a riesgo 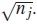. Así el estadístico de prueba queda:

La varianza puede estimarse como

Así, el estadístico para la prueba de Tarone-Ware está dado por:

2.9. Ponderaciones para las pruebas Log-Rank

La tabla 1 muestra las respectivas poderaciones de cada una de las pruebas Log-Rank estudiadas.

3. Potencia de las pruebas de hipótesis y estructuras de correlación

En esta sección se definen algunos conceptos relacionados con el objetivo de este trabajo.

3.1. Potencia de una prueba de hipótesis estadística

La prueba de hipótesis, generalmente, es usada para evaluar una hipótesis nula H₀ contra la hipótesis alternativa deseada H₁, considere

Entonces, si θ ∈ Θ₀ y la prueba de hipótesis decide en favor de H₁, es decir, se rechaza H₀, en este caso se comete un error de tipo I (con probabilidad α), o si 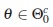y la prueba de hipótesis decide en favor de H₀, es decir, no se rechaza H₀, se comete un error de tipo II, (con probabilidad β), [9].

y la potencia está dada por:

3.2. Cópulas

Las cópulas se han convertido en una herramienta popular de modelamiento multivariado en muchos campos donde la dependencia multivariada es de gran interés y la usual normalidad multivariada puede no ser un supuesto razonable. Las cópulas han tenido un gran desarrollo debido a que permiten especificar las distribuciones marginales univariadas y su comportamiento por separado, [10].

Definición 1. Sea X y Y variables aleatorias con función de distribución conjunta F, con distribuciones marginales F₁ y F₂ respectivamente. X y Y son dos variables uniformes si F₁ y F₂ son continuas. Entonces existe una cópula única, la cual es una función de distribución acumulada, con sus marginales uniformes tal que

Las cópulas bidimensionales son funciones bivariadas que unen dos funciones de distribución univariadas para construir distribuciones bivariadas continuas. La cópula es una función que permite modelar la estructura de dependencia de dos variables aleatorias, [11].

3.3. Cópulas Arquimedianas

Si 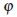(llamado un generador) es una función decreciente convexa, con una segunda derivada positiva, y 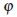(1)=0 y tal que

se puede entonces obtener una inversa (o cuasi-inversa si ϕ(0)< ∞) por medio de:

Una cópula Arquimediana se define entonces como C(u, v) = ϕ⁻¹ [ϕ(u) −ϕ (v)]. La tabla 2 lista algunas familias importantes de cópulas Arquimedianas con un solo parámetro, que se denotarán por C_θ, [12].

3.4. τ de Kendall

Definición 2 (Concordancia). Sean (xi, yi) y (xj, yj) dos observaciones de un vector de variables aleatorias continuas (X, Y ) se dice que (xi, yi) y (xj, yj) son concordantes si xi < xj y yi < yj o xi > xj y yi > yj. Esto es, (xi, yi) y (xj, yj) son concordantes si (xi − xj) (yi − yj) > 0, [12].

Definición 3 (Discordancia). Sean (xi, yi) y (xj, yj) dos observaciones de un vector de variables aleatorias continuas (X, Y ) se dice que (xi, yi) y (xj, yj) son discordantes si xi < xj y yi > yj o xi > xj y yi < yj. Esto es, (xi, yi) y (xj, yj) son discordantes si (xi − xj) (yi − yj) < 0, [12].

Definición 4 (τ de Kendall). Suponga que (X,Y ) y (X^* ,Y ^*) son dos observaciones independientes de una distribución conjunta. Entonces τ es la diferencia entre la probabilidad de concordancia y la probabilidad de discordancia de esas dos observaciones, esto es,

Se asumen que las distribuciones marginales son continuas, [11]. Se puede demostrar que −1 ≤ τ ≤ 1.

3.5. Cópula Frank

La cópula Frank, cuyo generador es φ(t)= −In[(exp(−θt) −1)] / (exp(−θ) −1)], está dada por:

con t ∈ [0,∞] y θ ∈ (0, ∞),

El uso de la cópula Frank es atractivo, ya que se puede capturar el rango completo de dependencia; esto es, al igual que la cópula Gaussiana, la cópula Frank incluye las cópulas de cota superior de Fréchet cuando θ →−∞, de cota inferior de Fréchet cuando θ → ∞ y de independencia cuando θ → 0. De hecho, cuando se trata de inferencia, algunos estadísticos prefieren usar la cópula Frank a la Gaussiana, ya que mientras ambas cópulas tienen propiedades similares, la cópula Frank proporciona cantidades cerradas y, por lo tanto, más fáciles de programar, [13].

Para evaluar el grado de asociación entre las marginales en el modelo generado por la cópula Frank, el τ de Kendall correspondiente está dado por:

donde D_k(x) es la función Debye, la cual está definida para cualquier entero _k por

El τ de Kendall de la cópula Frank toma valores en el rango completo de concordancia. Observando los casos especiales de la cópula Frank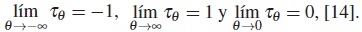

4. Estudio de simulación

Para determinar el comportamiento de las pruebas tipo Log-Rank, al ignorar o incluir la dependencia entre los tiempos de falla y censura se llevó a cabo un estudio de simulación. Los escenarios de simulación se describen a continuación:

(a) Los tamaños de muestra usados son: n = 30, 50,100, 200,400.

(b) Se definen dos variables aleatorias, T es el tiempo de falla y C es el tiempo de censura. Se consideran dos casos de interés:

b-1 T y C independientes. Se formarán dos bases de datos, cada una de las cuales consta de tres columnas (Tiempos (tiempos de falla), Estados (Indica si la observación está censurada o no), grupo (son dos grupos cada uno generado de una distribución Weibull, con parámetros diferentes)). Los pasos para conformar las bases de datos se listan a continuación:

1. Se generaron observaciones T_i, con i =1,2,...,n, de unas variables aleatorias T ∼ Weibull(η = 0,62, β = 1,6), las cuales corresponden a un grupo de tamaño n/2 y T ∼ Weibull(η = 1,9, β =1,9), las cuales corresponden a otro grupo de tamaño n/2. Donde η es el parámetro de localización y β el parámetro de escala.
2. Se generaron observaciones censuradas C_i con i =1,2,...,n, de una variable aleatoria C ∼ UNIF (0,bj) con j =1,2. b₁, se obtiene cuando se soluciona C⁺ usando los parámetros de la distribución Weibull η =0,62 y β =1,6, y b₂, se obtiene cuando se soluciona C⁺ usando los parámetros de la distribución Weibull η =1,9 y β =1,9. Sea C⁺=P (T > C) la fracción de censura, b se selecciona de tal forma que C⁺=0,20, 0,30, 0,40, 0,50.

Ahora tomando c ∼ UNIF(0,b), se obtiene:

Realizando cambio de variable se tiene, sea w =(c/η)^β entonces c = ηw^1/β y (η/β)aw^1/β−1dw =dc. Entonces,

Luego,

Donde, FG 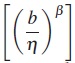es la función de distribución acumulada de una variable aleatoria Gamma con parámetro de forma 1/β y escala igual a 1. Ahora como β, η y C⁺ son dados, entonces (18) se soluciona numéricamente para obtener b.

b-2 T y C dependientes. Se formarán dos bases de datos, cada una de las cuales consta de tres columnas (Tiempos (tiempos de falla), Estados (Indica si la observación está censurada o no), grupo (son dos grupos cada uno generado de una distribución Weibull, con parámetros diferentes)). Los pasos para conformar las bases de datos se listan a continuación:

1. Se simularon tiempos de falla y censura aleatoria dependientes usando la cópula Frank, y parámetro de dependencia el τ de Kendall, con τ = 0.95, de forma tal que: las observaciones de falla Ti, con i =1,2,...,n, son variables aleatorias T ∼ Weibull (η =0,62, β =1,6) las cuales corresponden al primer grupo de tamaño n/2y T ∼ Weibull (η =1,9, β =1,9) las cuales corresponden al primer grupo de tamaño n/2. Donde η es el parámetro de localización y β el parámetro de escala, de tamaño n.

2. Se generaron observaciones censuradas C_i con i =1,2,...,n,de C ∼ UNIF(0,bj), con j =1, 2, b1, se obtiene cuando se soluciona C⁺ usando los parámetros de la distribución Weibull η =0,62 y β =1,6, y b₂, se obtiene cuando se soluciona C⁺ usando los parámetros de la distribución Weibull η = 1,9 y β =1,9. b se selecciona de tal forma que P(T > C) = C⁺=0,20, 0,30, 0,40, 0,50, la fracción de censura, con

Con S_T|C(c|c) la función de supervivencia de una distribución condicional de T en C =c, evaluada en c. C⁺ se soluciona numéricamente.

(c) En (b-2) y (b-1) se tiene que si Ti > Ci, la observación es censurada en Ci ySi Ti ≤ Ci, la observación falla en Ti

(d) Para cada una de las bases de datos conformadas se calcula la función de supervivencia usando el método de Kaplan-Meier, y luego se calculan las diferentes pruebas Log-Rank de las que se registra el valor p, para cada prueba se realizan k =1000 simulaciones.

(e) Con los valores p que se registran se realiza el estudio de potencia y se calcula el tamaño de la prueba de las respectivas pruebas tipo Log-Rank, la potencia se calcula como se muestra a continuación: las pruebas Log-Rank nos permiten probar H₀: S_T1 =S_T2 contra H₀: ST₁ ≠ST₂ con T1 ∼ Weibull (0,62, 1,6) y T2 ∼ Weibull (1,9, 1,9), la simulación se hace bajo la hipótesis alterna (T2 ∼ Weibull (1,9, 1,9)).

Con k el número de simulaciones y P( rechazar H₀ | H₀ es falsa) equivale al número de veces que se rechaza H₀ y para el cálculo del tamaño de la prueba se considera H₀ como cierta (T1 ∼ Weibull (0,62,1,6)) y se calcula como 1 Potencia.

5. Resultados del estudio de simulación

5.1. Estudio de potencia

Se presenta la potencia estimada alcanzada por las diferentes pruebas de hipótesis realizadas, para los porcentajes de censura C⁺=0,2y0,5, se observa que al aumentar el tamaño de muestra la potencia estimada de la prueba aumenta tanto para cuando se tienen tiempos de falla y censura dependientes e independientes. Los resultados presentados en esta sección se realizan teniendo en cuenta τ =0,95.

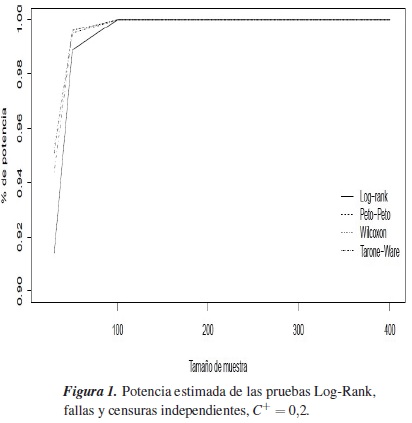
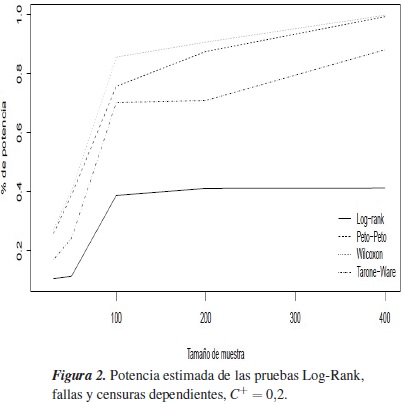
Cuando se tiene porcentaje de censura de C⁺= 0,2, se evidencia que la potencia de las pruebas Log-Rank para tiempos de falla y censura independientes es superior al 90%, mientras que para tiempos de falla y censura dependientes la potencia está entre 10% y 80%, como se muestra en la tabla 3, para este último caso la prueba que menor potencia presenta es la Log-Rank indistintamente del tamaño de muestra.

TABLA 3

En la figura 1 se muestra la potencia estimada para todas las pruebas cuando las fallas y las censuras son independientes y se tiene porcentaje de censura C⁺=0,2, en esta se puede observar a partir de un tamaño de muestra de n =100, que la potencia es igual a 100%, para tamaños de muestra de n =30 y n =50, la prueba que mayor potencia tiene es la de Wilcoxon y la que menor potencia tiene es la Log-Rank.

En la figura 2 se muestra la potencia estimada para todas las pruebas cuando las fallas y las censuras son dependientes y se tiene porcentaje de censura C⁺=0,2, la prueba que mayor potencia estimada presenta es la prueba de Wilcoxon, y la que menor potencia estimada alcanza es la prueba Log-Rank, para los tamaños de muestra n =30,50 las potencias son inferiores al 40%.

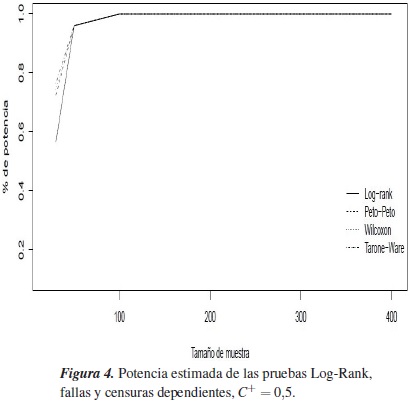
En la tabla 4, se muestra la potencia estimada de las pruebas Log-Rank, con porcentaje de censura C⁺ = 0,5.

TABLA 4

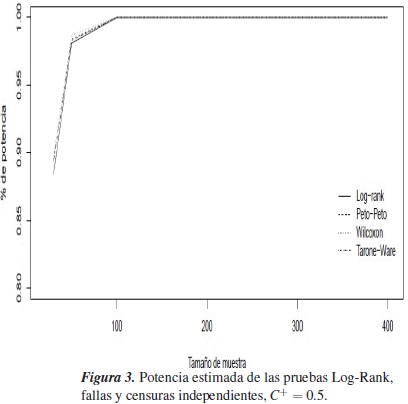
Las figuras 4 y 3, respectivamente, para tiempos de falla y censura independientes y dependientes, la potencia estimada para las pruebas Log-Rank en un mismo eje de coordenadas. Las pruebas alcanzan una potencia estimada muy similar, están entre el 88% y el 100%, cuando los tiempos de falla y censura son independientes, y cuando son dependientes la potencia estimada está entre el 76% y el 100%.

Note que a medida que el porcentaje de censura aumenta, la potencia estimada de las pruebas para fallas y censuras independientes disminuye (pequeña disminución), pero para fallas y censuras dependientes la potencia aumenta, este hecho se debe a que aunque se tienen más censuras (ausencia de experimentar el evento de interés), se tiene información de por qué no se observa el evento de interés.

6. Conclusiones

En este estudio se evaluó el desempeño de algunas pruebas tipo Log-Rank en presencia de censura informativa a partir de los resultados de simulación; se observó que cuando los tiempos de falla y censura son independientes, la potencia de las pruebas disminuye (una disminución pequeña), a medida que el porcentaje de censura aumenta. Además, cuando los tiempos de falla y censura son dependientes (censura informativa), la potencia de las pruebas aumenta, a medida que el porcentaje de censura aumenta, pero cuando el porcentaje de censura es de 0,2, 0,3, 0,4, 0,5 y los tamaños de muestra son inferiores a 100, la potencia es inferior a 70%, lo anterior bajo las distribuciones simuladas.

Otro aspecto importante en este estudio es que la censura informativa es un fenómeno que se presenta en la práctica con mucha más frecuencia de lo que se cree, por ejemplo, en un ensayo clínico controlado longitudinal en el que una gran proporción de individuos abandonan el estudio antes de la observación del seguimiento debido a los fuertes efectos secundarios de un tratamiento específico; así, los resultados presentados son de vital importancia si los estudios presentan las condiciones de los escenarios simulados. De acuerdo con los resultados del estudio de simulación se recomienda, en presencia de censura informativa, el uso de la prueba de Wilcoxon.

7. Agradecimientos

Los autores agradecen los valiosos comentarios y recomendaciones del profesor Luís Alberto Escobar de Louisiana State University que ayudaron a mejorar el manuscrito. También agradecemos de manera muy especial a la Escuela de Estadística de la Universidad Nacional de Colombia, Sede Medellín, por todo el apoyo durante el curso de esta investigación.

Referencias

[1] D. Collett, "Modelling Survival Data in Medical Research", Chapman & Hall, New York, 2003.         [ Links ]

[2] D. G. Kleinbaum, "Survival analysis", Springer, Verlag, New York, 1995.         [ Links ]

[3] P. D. Allison, "Survival Analysis Using the SAS System: A Practical Guide", SAS Institute Inc, New York, 2000.         [ Links ]

[4] M. Pintilie, "Competing Risks", John Willey & Sons, England, 2006.         [ Links ]

[5] M. Tableman, and J. Sung, Survival Analysis Using S, Chapman & Hall, New York, 2003.         [ Links ]

[7] R. Peto and J. Peto, "Asymptotically Efficient Rank Invariant Test Procedures", Journal of the Royal statistical Society, vol. 135, pp. 185-207, 1972.         [ Links ]

[8] R. E. Tarone, and J. Ware, "On distributionfree tests for equality of survival distributions", Biometrika, vol. 64, pp. 156-160, 1972.         [ Links ]

[9] A. Davey, and Savla J., "Statistical power analysis with missing data: a structural equation modeling approach", Routledge Taylor & Francis Group, New York, 2010.         [ Links ]

[10] J. Yan, "Enjoy the Joy of Copulas", Journal of Statistical Software, vol. 21, pp. 1-21, 2007.         [ Links ]

[11] D. M. Dominique, and S. Kotz, "Correlation and Dependence", Imperial College Press, London, 2005.         [ Links ]

[12] R. B. Nelsen, "An introduction to Copulas", Springer, New York, 2006.         [ Links ]

[13] G. Escarela and J. Carriere, "Fitting competing risks with an assumed copula", Statistical Methods in Medical Research 12, New York, 2003.         [ Links ]

[14] C. Genest, "Frank's Family of Bivariate Distributions", Biometrika, vol. 74, pp. 549-555, 1987.         [ Links ]