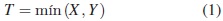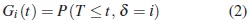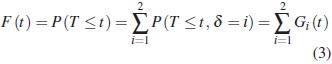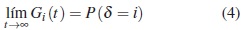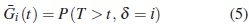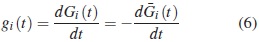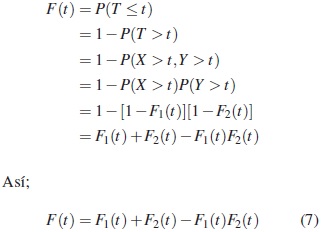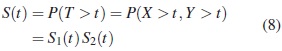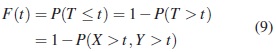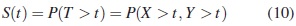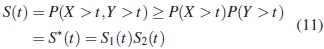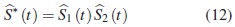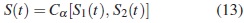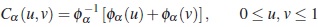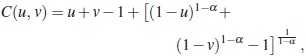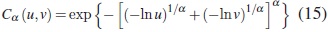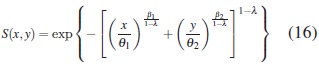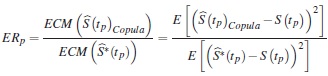Aplicación del estimador cópula gráfico en juveniles de bocachico Prochilodus magdalena sometidos a diferentes niveles de salinidad

Application of the Copula-Graphic Estimator in Juvenile Bocachico Prochilodus Magdalenae Subjected to Different Levels of Salinity

O. Bru Cordero^a,*
H. Brango García^b
M. C. Jaramillo Elorza^a
M. P. López^b

^a Escuela de Estadística, Universidad Nacional de Colombia, Sede Medellín, Colombia.
^* Autor de correspondencia: oebruc@unal.edu.co
^b Departamento de Matemáticas y Estadística, Universidad de Córdoba, Colombia.

Recepción: 01-oct-2015 Aceptación: 20-dic-2015

Resumen

En este trabajo se estima la función de supervivencia bajo dependencia mediante el estimador cópula-gráfico propuesto por [2]. Se hace un estudio de simulación para tiempos de falla Weibull con dos modos de falla y diferentes porcentajes de censura, donde se compara la función de supervivencia mediante el estimador cópula-gráfico con la estimación de la supervivencia, asumiendo independencia entre dos modos de falla. Se muestra una aplicación de un estudio realizado en el Centro de Investigación Piscícola de la Universidad de Córdoba-CINPIC, en el cual se quiere analizar la mortalidad de juveniles de bocachico sometidos a diferentes niveles de salinidad, que constituyen los modos de falla o causas de muerte (10 ppm y más de 12 ppm). Se encontró que asumiendo independencia en los modos de falla la función de supervivencia subestima la verdadera supervivencia, que es estimada de manera confiable con el estimador copula gráfico, ya que sí tiene en cuenta la dependencia entre los modos de falla.

Palabras clave: estimador cópula gráfico, censura, función de superviencia.

Abstract

In this paper, it is estimated the role of survival under dependence using the copula-graphic estimator proposed by [2]. A simulation study is carried out for Weibull failure times, with two failure modes and different percentages of censorship, where the survival function is compared through the copula-graphic estimator, with the survival estimation assuming independence from two failure modes. It is shown a study application carried out in the Fishing Research Center of the University of Cordoba-CINPIC (Colombia), in which the mortality of juvenile fish subjected to different levels of salinity is wanted to be analyzed, and what constitutes the failure modes or causes of death (10 ppm and 12 ppm). It was found that assuming independence in the failure modes the survival function, underestimates the true survival rate, which is estimated in a reliable manner with the estimator copula graphic, in which the dependency between the failure modes is taken into account.

Key words: Censored, Estimator Copula-Graphic, Survival Function.

1. Introducción

Los estimadores para el análisis de supervivencia requieren de independencia entre los modos de falla, lo que en riesgos competitivos hace referencia a censuras aleatorias independientes, a diferencia de los estimadores que utilizan funciones cópula, los cuales son consistentes en presencia de riesgos competitivos dependientes. Las funciones cópula bidimensionales son funciones bivariadas que unen o, bien, "copulan" dos funciones de distribución univariadas para construir funciones de distribución bivariadas continuas.

La cópula representa una forma paramétrica conveniente para modelar la estructura de dependencia en distribuciones conjuntas de variables aleatorias, en particular para parejas de variables aleatorias. Este concepto de cópula permite construir modelos diferentes a los conocidos en el análisis de dependencia entre variables estocásticas. La metodología de cópula es capaz de capturar relaciones no lineales y, en particular, permite relacionar eventos extremos que ocurren en la naturaleza. En el caso no paramétrico, la distribución conjunta para un problema con múltiples modos de falla no puede ser completamente identificada en la situación usual cuando solo se conocen los tiempos mínimos de falla, [3]. Incluso en el caso paramétrico, los datos pueden contener poca información sobre el coeficiente de asociación entre las variables, y resulta necesario hacer algunos supuestos al respecto [4]. Para el caso no paramétrico el estimador cópula gráfico de [2] resuelve el problema bajo el supuesto del conocimiento de la forma funcional de la cópula, que proporciona la estructura de asociación entre los riesgos competitivos. Es de anotar que bajo independencia el problema de identificabilidad no existe.

En este trabajo se estima la función de confiabilidad bajo dependencia mediante el estimador cópula gráfico propuesto por [2]. Se hace un estudio de simulación para tiempos de falla Weibull a diferentes porcentajes de censura y se compara el estimador cópula gráfico que permite incorporar la dependencia entre los modos de falla, con el que considera independencia (Kaplan Meier) entre los modos de falla en un estudio realizado en Acuicultura en el cual se quiere analizar la mortalidad de juveniles de boca-chico sometidos a diferentes niveles de salinidad (10 ppm y más de 12 ppm).

En virtud de tal consideración, no existen estudios que evaluen el desempeño de esta especie en aguas salobres en ninguna etapa de su vida; sin embargo, es frecuente el uso de soluciones salinas para tratar algunas epizootias relacionadas con hongos; el procedimiento consiste en preparar solución salina con NaCl e introducir los peces a un rápido baño en ella. La mayoría de las veces estos tratamientos se aplican sin conocer la tolerancia de la especie a las concentraciones de salinidad y el tiempo de exposición. Por lo que el desconocimiento de las concentraciones salinas que pueden soportar los juveniles de bocachico podrían estar impidiendo que se apliquen tratamientos profilácticos más efectivos para prevenir patologías, o, por el contrario, se esté deteriorando su salud con dicho tratamiento y, en algunos casos, ocasionando la muerte del pez.

2. Riesgos competitivos

El tiempo de falla de un sistema con dos modos de falla puede ser modelado como un sistema en serie o un modelo de riesgos competitivos. Cada unidad tiene un tiempo potencial de falla asociado a cada modo de falla. El tiempo de falla observado es el mínimo de esos tiempos potenciales individuales. Por ejemplo, para un sistema con dos modos de falla, sean X y Y los respectivos tiempos potenciales, entonces el tiempo de falla observado es:

De esta manera, en la práctica solo se observa el mínimo entre X y Y, pero se conoce cuál es el modo de falla. Así los datos son parejas de la forma (T, δ), donde: T = mín (X,Y ) y δ es una variable discreta que representa el modo de falla, que toma valores de 0 cuando se presenta una censura a derecha, 1 cuando falla debido al primer modo de falla, y 2 cuando falla debido al segundo modo de falla. Para estudiar este modelo de riesgos competitivos, es necesario presentar algunas funciones básicas.

Función de subdistribución

Para un evento de tipo i (i =1, 2), la función de subdistribución es definida como la probabilidad conjunta:

En otras palabras, la función de subdistribución es la probabilidad de que un evento de tipo i ocurra hasta el tiempo t. La función de distribución conjunta es la probabilidad de que un evento de cualquier tipo ocurra hasta el tiempo t,, es decir, es igual a la suma de las funciones de subdistribución para todos los tipos de eventos, así:

Nótese que cuando hay riesgos competitivos la función de distribución total se encuentra en el intervalo [0,1]. En contraste, en presencia de los riesgos competitivos la función de subdistribución solo toma valores hasta P ( δ = i ), debido a que

Función de supervivencia

Es la probabilidad de que un evento de tipo i no ocurra hasta el tiempo t , es decir, se define como la probabilidad de que un evento de tipo i no haya sido observado hasta el tiempo t:

Función de subdensidad

La función de subdensidad para el modo de falla i y T continuo se define como:

2.1. Riesgos en competencia con censura aleatoria a derecha

En riesgos competitivos, el resultado observado comprende T , el tiempo de falla, y δ, el tipo de causa o modo de falla. T es una variable aleatoria continua positiva, y δ puede tomar un número fijo pequeño de valores i = 1,2,...,p. La distribución de probabilidad es bivariada con δ discreta y T continua. Se asume que a cada falla puede asignarse una y solo una causa del conjunto de p causas.

2.2. Estimador bajo independencia para la función de supervivencia

Una estructura en serie con s componentes funciona, si y solo si, todas las componentes funcionan. Para un sistema en serie con dos componentes independientes en serie, la función de distribución es

donde ( X,Y ) son los tiempos de vida asociados a las dos componentes y F_i, i = 1, 2 son, respectivamente, las funciones de distribución para las componentes, y T = mín ( X,Y ) es el tiempo de falla observado del sistema.

La función de confiabilidad S(t)= 1 − F(t) para el caso de independencia es:

donde Si (t), i = 1, 2 son las funciones de confiabilidad para las dos componentes. Para un sistema con dos componentes en serie y tiempos de falla dependientes

En este caso, la evaluación debe hacerse con respecto a la distribución conjunta de X y Y , que incluyen los parámetros de dependencia. La función de confiabilidad para este caso es:

Para modos de falla en competencia, con dependencia positiva se sabe que, [5],

donde S^*(t)es la función de supervivencia asumiendo independencia. Por lo tanto S^*(t)es pesimista en relación con S (t), esto es para un mismo tiempo t, la probabilidad de supervivencia bajo el supuesto de independencia está siempre por debajo de la probabilidad conjunta que incluye la dependencia. El estimador de S^*(t)se denotará 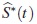, que es un estimador de la confiabilidad del tiempo mínimo de falla de un sistema con dos modos de falla que compiten. Este se obtiene como el producto de las funciones de confiabilidad estimadas bajo una distribución específica, donde para cada función marginal se estiman los parámetros, considerando los tiempos del otro modo de falla como tiempos de censura, así:

donde 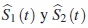se supone son las funciones de confiabilidad marginales estimadas para cada modo de falla.

2.3. Cópulas

Los modelos cópula son clases de distribuciones de supervivencia bivariada, especificada en términos de las funciones de supervivencia marginal y una función cópula, que es una función de distribución continua bivariada sobre el cuadrado unitario [0, 1] con marginales uniformes. Una característica de la clase cópula es que la determinación de las marginales a través de la cópula ayuda a modelar y entender eficazmente la estructura de dependencia, [6]. En el contexto de riesgos competitivos es posible especificar la distribución de supervivencia conjunta en términos de dos distribuciones de supervivencia marginal y una cópula que permite relacionar la dependencia entre las variables aleatorias individuales que corresponden a cada riesgo de falla [6]. Luego, sea la cópula de supervivencia C_α con α ∈ R para dos variables aleatorias X y Y , donde α representa el parámetro de dependencia entre las dos variables. Si (X, Y ) proviene de una cópula para algún α, entonces la función de supervivencia conjunta de (X, Y ) está dada por

Teorema 1 (Teorema de Sklar). Sean X, Y variables aleatorias con función de distribución conjunta F, con marginales F₁ y F₂, respectivamente. Entonces existe una cópula C que satisface

para toda y₁, y₂ ∈ R. Si F₁ y F₂ son continuas, entonces C es única. Inversamente, si C es una cópula, y F₁, F₂ son funciones de distribución, entonces F definida en la ecuación (14) es una función de distribución conjunta con marginales F₁ y F₂.

El teorema establece que, en el contexto de parejas de variables aleatorias continuas, es posible construir una función de distribución bivariada en términos de dos funciones de distribución continuas univariadas y una cópula que permite relaciones de dependencia entre dos variables aleatorias individuales. Una demostración del Teorema de Sklar puede encontrarse en [7].

2.4. Familias cópula

2.4.1. Cópulas arquimedianas

Una distribución bivariada perteneciente a la familia de modelos cópulas arquimedianas tiene la representación

donde φ_α es convexa y decreciente tal que φ_α ≥ 0, φ_α (1)=0. A la función φ_α se le denomina generador de la cópula C_α, y la inversa del generador φ_α⁻¹ es la transformada de Laplace de una variable latente, la cual induce la dependencia α. Así, la selección de un generador resulta en varias familias cópulas.

2.4.2. Cópula Gama

La cópula gamma, que se utiliza en este trabajo, tiene la siguiente forma:

con α > 1 donde u y v son funciones de distribución marginal para los tiempos de falla X y Y . α es el parámetro de dependencia de la cópula, el cual mide el grado de asociación entre los tiempos de falla [2], mostraron que el estimador cópula gráfico es robusto a la selección de la cópula, es decir, se puede tomar cualquier cópula de la familia arquimediana. Se usa la cópula por su fácil programación. La cópula gama permite variables con rango (0, ∞)como es el caso de la distribución Weibull, que es de amplio uso en confiabilidad o sobrevivencia.

2.4.3. Familia Gumbel

La función de confiabilidad bivariada perteneciente a la familia Gumbel (1960) tiene la forma

donde 0 < α < 1. Aquí φ_α⁻¹ (s) = exp (−s^α ) es la transformada de Laplace de una distribución estable positiva. Valores pequeños de α producen alta correlación y T₁ y T₂ son independientes cuando α → 1.

3. Bioecología del Bocachico (Prochilodus magdalenae)

El bocachico (Prochilodus magdalenae) esunpez cuyo hábitat está restringido a las aguas dulces, [8]; desarrolla su ciclo biológico tanto en las ciénagas o planos inundables, donde se alimenta y crece. No existen reportes de distribución de esta especie en hábitats diferentes a los cuerpos de aguas dulces, aguas continentales, como, por ejemplo, estuarios, ciénagas costeras y marismas, entre otras.

La mayoría de los peces solo toleran salinidades similares a aquellas en las que residen. Sin embargo, hay algunas especies capaces de sobrevivir en un amplio rango de salinidades; se denominan eurihalinas, y los movimientos que realizan a zonas de distintas salinidades están asociados, a menudo, con su ciclo vital. Existen dos tipos de especies eurihalinas: las que toleran y se adaptan a fluctuaciones rápidas de la salinidad externa, y las que realizan migraciones en algún período de su ciclo vital entre medios dulceacuícolas y marinos. Las primeras viven es estuarios, salinas y zonas litorales y pueden experimentar cambios desde agua de mar a agua dulce en el tiempo de un ciclo mareal. El segundo grupo lo conforman las especies que requieren de cambios fisiológicos a largo plazo (e irreversibles) cuando realizan migraciones desde distintas salinidades ambientales (los salmónidos, por ejemplo) [9].

Las especies de agua dulce pueden tener cierto beneficio en su punto isosmótico, pero por encima de esta concentración, el crecimiento máximo desciende bruscamente. Salinidades del 15 ppm pueden ser letales por razones osmóticas e iónicas. Los peces pueden regular sus iones plasmáticos de tal forma que la concentración osmótica interna de sus fluidos (entre 300 y 400 mOsm/Kg) sea equivalente al 10 o 12 ppm de salinidad, dependiendo de la tolerancia, capacidad de regulación y salinidad ambiental [10].

3.1. Reproducción en peces

La cría de peces de agua dulce poslarvas en agua ligeramente salinizadas tiene algunos beneficios, como la reducción de las enfermedades de la intolerancia a la salinidad y la posibilidad de utilizar los alimentos marinos vivos como Artemia sp; [11]. Este alimento tiene una alta calidad nutricional [12] y la tecnología de cultivo ya está disponible, [11]. La supervivencia en agua ligeramente salinizadas se extiende, lo que aumenta en los peces de alimentación, y reduce los problemas de mala calidad del agua causada por la muerte de Artemia sp. y descomposición [13]. Otra ventaja está relacionada directamente con la osmorregulación de los peces. Agua salinizadas reduce el gradiente osmótico y, en consecuencia, reduce el consumo de energía y promueve el aumento del crecimiento [1]. Para peces de agua dulce, el gradiente osmótico bajo representa una reducción de aproximadamente 20% a 40% en la tasa metabólica, debido a menor metabolismo y menor consumo de energía para producir orina abundante en agua dulce [1].

4. Generación de los tiempos de falla Weibull bivariado con diferentes porcentajes decensura

Para simular los tiempos de falla Weibull bivariados se usó el algoritmo cópula compuesta de Gumbel-Hougaard, [15]. La función de supervivencia conjunta de la Weibull bivariada utilizada es [14].

donde T₁ > 0 y T₂ > 0 son tiempos de falla Weibull; β₁ > 0 y β₂ > 0 son los parámetros de forma; θ₁ > 0 y θ₂ > 0 son los parámetros de escala asociados a X y Y , respectivamente; 0≤ λ ≤ 1 es el parámetro de dependencia entre X y Y . Cuando el parámetro de dependencia λ entre los tiempos de falla Weibull es 0, entonces hay independencia entre X y Y .A medida que λ aumenta, la dependencia entre X y Y aumenta.

Los casos de tiempos de falla Weibull que se estudiaron difieren de acuerdo con la forma de la función hazard de los tiempos de falla. Se estudiaron 4 casos, los valores de los parámetros de escala θ_i serán de 1, ya que la forma de la función hazard de tiempos de falla Weibull depende del parámetro de forma βi. Los casos estudiados fueron:

Tiempos de falla con parámetros de forma βi diferentes. Modo de falla con tasa de falla decreciente vs. Modo de falla con tasa de falla creciente: β₁ =0,5 y β₂ =2.

Tiempos de falla con parámetros de forma βi diferentes. Modo de falla con tasa de falla decreciente vs. Modo de falla con tasa de falla constante: β₁ =0,5 y β₂ =1.

Tiempos de falla con parámetros de forma βi iguales. Modo de falla con tasa de falla decreciente vs. Modo de falla con tasa de falla decreciente: β₁ =0,5 y β₂ =0,5.

Tiempos de falla con parámetros de forma βi diferentes. Modo de falla con tasa de falla creciente vs. Modo de falla con tasa de falla constante: β₁ =2 y β₂ =1.

Asociados a los 4 casos de tiempos de falla Weibull mostrados anteriormente, tenemos 3 situaciones diferentes con respecto al parámetro de dependencia λ entre tiempos de falla Weibull, se tomaron los siguientes valores: λ =0,25, 0,50, 0,75.

Se estima la función de supervivencia, asumiendo independencia entre los modos de falla con el estimador 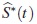y bajo dependencia, asumiendo un modelo cópula con el estimador .

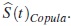El esquema que se utilizó para las estimaciones es el siguiente:

Se generan muestras de tamaño n =100 de tiempos bivariados Weibull.

En cada una de las muestras de tiempos bivariados obtenidas se toma el tiempo mínimo y se etiqueta cada uno de estos tiempos con 1 ó 2, para indicar si ese tiempo proviene de los tiempos del modo de falla 1, o si ese tiempo proviene de los tiempos del modo de falla 2.

Teniendo los modos de falla se introdujo el porcentaje de censura, colocando 0 de manera aleatoria en los tiempos de falla; una censura quiere decir que no se presentó el evento de interés por ninguno de los dos modos de falla.

Se estiman los parámetros asociados a las distribuciones de los tiempos de falla de cada modo de falla, con estos se estiman las funciones de supervivencia del tiempo mínimo de falla para cada uno de los casos de interés, mediante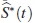

Se estiman las distribuciones marginales asociadas a cada modo de falla mediante la aplicación del algoritmo cópula gráfico, y con estas funciones de distribución marginales se obtiene .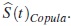

Se comparan puntualmente los dos estimadores, calculando la eficiencia relativa (ER_p) del estimador bajo independencia con relación al cópula gráfico en los percentiles p =0,05, 0,25, 0,50, 0,75, 0,95, con la siguiente ecuación:

donde 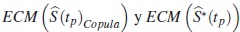son los errores cuadrático medio que estiman la dispersión de las diferencias entre la función de supervivencia verdadera y los estimadores 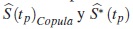respectivamente.

Si ER_p < 1, entonces 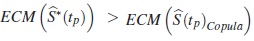, lo cual indicará que 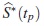es menos eficiente frente a 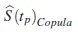para la estimación de la función de supervivencia verdadera en t_p.

5. Resultados de la simulación

En las tablas 1 a 4 se muestran los calculos de la eficiencia relativa ER_p del estimador 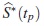con relación a 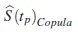en los percentiles p = 0,05, 0,25, 0,50, 0,75 y 0,95, con diferentes porcentajes de censura ( 25%, 50% y 75%) y teniendo en cuenta la dependencia entre los dos modos de falla (0,25, 0,50 y 0,75). En estas tablas no se observa algún patron definido en los resultados de la eficiencia relativa a medida que la dependencia aumenta. Se observa que el estimador 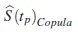es mejor que 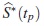al momento de estimar 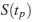en todos los casos estudiados para una distribución Weibull, puesto que siempre la ER_p es menor que 1, lo cual nos asegura que la dispersión del estimador 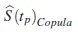comparado con 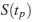siempre es menor que la dispersión de estimador 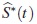con relación a .

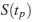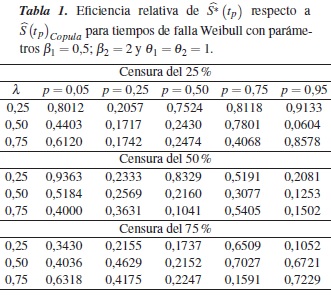
En la tabla 1 se muestra la eficiencia relativa (ER_p) del estimador 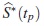con relación a 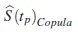en los percentiles p = 0,05, 0,25, 0,50, 0,75 y 0,95, para el caso de una Weibull con parámetros β₁ = 0,5; β₂ = 2 y θ₁ = θ₂ = 1, dependencia λ = 0,25, 0,50, 0,75 y porcentajes de censura de 25%, 50% y 75%; en esta se observa que en todos los casos la eficiencia relativa es menor que 1, es decir, el estimador 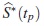es menos eficiente que 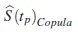para estimar .

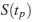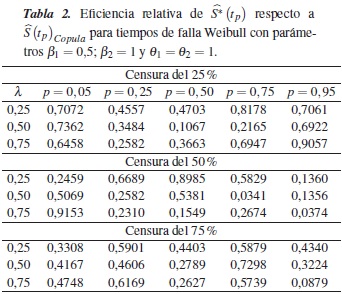
En la tabla 2 se muestra la eficiencia relativa (ER_p) del estimador 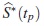con relación a 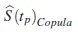en los percentiles p = 0,05, 0,25, 0,50, 0,75 y 0,95, para el caso de una Weibull con parámetros β₁ = 0,5; β₂ = 1 y θ₁ = θ₂ = 1, dependencia λ = 0,25, 0,50, 0,75 y porcentajes de censura de 25%, 50% y 75%; en esta se observa que en todos los casos la eficiencia relativa es menor que 1, por lo tanto, el estimador 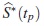es menos eficiente que 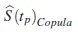para estimar .

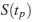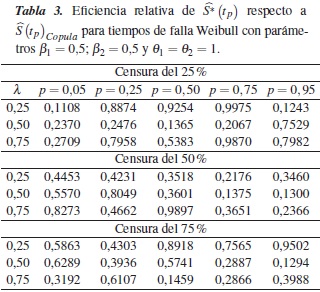
En la tabla 3 se muestra la eficiencia relativa (ER_p) del estimador 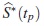con relación a 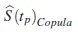en los percentiles p = 0,05, 0,25, 0,50, 0,75 y 0,95, para el caso de una Weibull con parámetros β₁ = 0,5; β₂ = 0,5 y θ₁ = θ₂ = 1, dependencia λ = 0,25, 0,50, 0,75 y porcentajes de censura de 25%, 50% y 75%; en esta se observa que en todos los casos la eficiencia relativa es menor que 1, así podemos concluir que el estimador 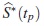es menos eficiente que 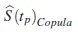para estimar .

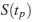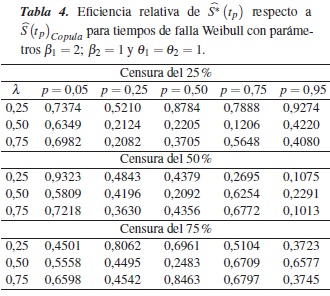
En la tabla 4 se muestra la eficiencia relativa (ER_p) del estimador 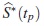con relación a 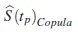en los percentiles p = 0,05, 0,25, 0,50, 0,75 y 0,95, para el caso de una Weibull con parámetros β₁ = 2; β₂ = 1 y θ₁ = θ₂ = 1, dependencia λ = 0,25, 0,50, 0,75 y porcentajes de censura de 25%, 50% y 75%; en esta se observa que en todos los casos la eficiencia relativa es menor que 1, así podemos concluir que el estimador 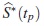es menos eficiente que 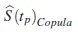para estimar .

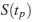Es importante destacar que, tomando como referencia los porcentajes de censura, a medida que estos aumentan, el número de casos donde la eficiencia relativa está cercana a uno disminuye notablemente, es decir, en el 25% hay 12 casos donde la eficiencia es cercana a uno, en el 50% se presentan 9 casos y en el 75% existen solo cuatro casos.

6. Aplicación

Para la realización del experimento se utilizaron juveniles de bocachico (Prochilodus magdalenae) provenientes de reproducción artificial con aproximadamente 30 días de edad y longitud entre 3 y 4 cm. Las unidades experimentales fueron acuarios de vidrio de 10 litros de volumen útil, dotados de aireación permanente. Los alevinos fueron sembrados a razón de un individuo por litro y previamente se mantuvieron en un tanque de 500 litros durante 24 horas para adaptarlos a las condiciones de temperatura.

Los juveniles de bocachico fueron sometidos a diferentes niveles de salinidad: 0, 2, 4, 6, 8, 10, 12 y 14 ppm. Para obtener estas salinidades se preparó una solución salina patrón de 20 ppm de NaCl. A partir de esta solución patrón, mediante diluciones se obtuvieron las demás salinidades agregando gradualmente a cada unidad experimental la cantidad de solución salina patrón hasta completar el volumen y la salinidad deseada. Al final, las diferentes salinidades fueron verificadas mediante un refractómetro. El ensayo tuvo una duración de 24 horas y se hizo el seguimiento a cada una de las unidades experimentales al final de cada hora y contabilizando el número de alevinos muertos. Previamente, se realizaron tres ensayos para determinar los niveles de salinidad que se tomarían como referencia, teniendo en cuenta que los peces presentan de 8 a 9 ppm de sal en la sangre y que la descompensación del sistema osmorregulador del pez ocurre en estos niveles; por tanto, se tomó como primer modo de falla 10 ppm de salinidad y como segundo modo de falla de 12 a 14 ppm. Se estimaron las funciones de supervivencia mediante dos estimadores: en el primero se asumió independencia entre los dos modos de falla, y en el segundo se tuvo en cuenta la dependencia existente entre estos dos modos de falla (cópula-gráfico).

7. Resultados

Se estimaron las funciones de supervivencia mediante dos estimadores; en el primero se asumió independencia entre los dos modos de falla, y en el segundo se tuvo en cuenta la dependencia existente entre estos dos modos de falla, así como las funciones de distribución marginal asociadas a cada modo (causa de muerte).

Baldisserotto (2002) ha encontrado que existe en peces de agua dulce una dependencia cuando son sometidos a ambientes salobres, lo cual influye en el gradiente osmótico del pez, aproximadamente hasta el 40% en la tasa metabólica. Además, se asume un 10% en variables ambientales del experimento, las cuales también afectan la supervivencia del animal; por tal razón, en este trabajo asumimos una dependencia de 50% entre los juveniles sometidos a un nivel de salinidad de 10 ppm y los sometidos a salinidad entre 12 y 14 ppm. Por ende, el parámetro de dependencia con el cual se realizó la estimación de la función de supervivencia con el estimador cópula gráfico es de λ = 0,5.

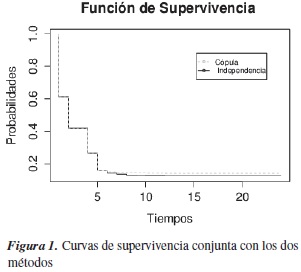
En la figura 1 se muestran los gráficos con las estimaciones de las funciones de supervivencia con los dos casos, asumiendo independencia entre los niveles de salinidad y teniendo en cuenta la dependencia entre estos niveles.

Las dos curvas de supervivencia son parecidas, solo después de la hora 6 la curva de supervivencia estimada mediante el cópula gráfico está por encima de la supervivencia estimada con independencia; hasta la hora 6 las estimaciones son las mismas. La mayoría de los alevinos, hasta la hora 5, ya habían muerto, a esa hora tienen una probabilidad de sobrevivir de 20%.

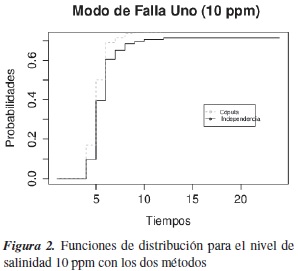
En las figuras 2 y 3 se estiman las funciones de distribución marginal asociadas a cada modo de falla con los dos métodos. Para el modo de falla 1 las dos curvas difieren en algunos periodos de tiempo; una prueba formal para probar si las curvas son diferentes es la prueba de logrank, que nos arroja que las curvas no son diferentes. Pero en relación con lo probado por [16], donde bajo verdadera dependencia entre los modos de falla y si se asume independencia entre dos modos de falla, lo que se estima realmente no son marginales, como lo demostraron ellos mediante simulación estadística para datos Weibull bivariados.

Con el nivel de salinidad de 10 ppm, a la hora 5 de inspección la probabilidad de muerte de los alevinos es de 18%, y a la inspección en la hora 6 la probabilidad es de 50%. Con el segundo nivel de salinidad, de 12 a 14 ppm (modo de falla dos), los alevinos murieron muy rápido: a la hora 6 la probabilidad estimada de muerte fue de 80%; en la primera hora ya había muerto el 40% de los alevinos.

8. Conclusiones

Las curvas de supervivencia con el estimador cópula gráfico y con el estimador independencia son estadísticamente iguales debido a que casi todos los alevinos murieron a causa de un modo de falla (12 a 14 ppm).

Para estimar las distribuciones marginales asociadas a los modos de falla no es recomendable trabajar con el supuesto de independencia cuando estos modos de falla son realmente dependientes, como lo probaron mediante simulación para datos Weibull bivariados [16] y lo reafirmamos en este estudio mediante una aplicación con datos reales.

Se reafirma lo encontrado por [16], donde probaron que el estimador cópula gráfico estima mejor la supervivencia conjunta con dos modos de falla dependientes. En este caso no tuvieron en cuenta los porcentajes de censura.

El nivel de salinidad adecuado para la eficiencia en el manejo de la alimentación y de las enfermedades es de 10 ppm, con un tiempo aproximado de exposición de 4 horas.

Referencias

[1] B. Baldisserotto, Fisiología Aplicada a Peixes Piscicultura, Ed. UFSM, Santa Maria, 2002.         [ Links ]

[2] M. Zheng, M. and J. Klein, "Estimates of marginal survival for dependent competing risks based on an assumed copula", Biometrika, vol. 82, no. 1, pp. 12-38, 1995.         [ Links ]

[3] A. Tsiatis, A nonidentifiability aspect of the problem of competing risks, 2da Edn, Ed Proc. Natl. Acad. Sci., USA, 1975.         [ Links ]

[4] W. Meeker, L. Escobar, and Y. Hong, "Using Accelerated Life Tests Results to Predict Product Field Reliability", Technometrics, vol. 52, no. 1, pp. 146-161, 2009.         [ Links ]

[5] R. E. Barlow, and F. Proschan, Statistical Theory of Reliability and Life Testing, Ed Holt, Richard Winston. Sci., New York, 1975.         [ Links ]

[6] G. Escarela, y J. Carriere, "Fitting Competing risks with an assumed copula", Statistical Methods in Medical Research, vol. 12, no. 4, pp. 333-349, 2003.         [ Links ]

[7] B. Schweizer, and A. Sklar, Probabilistic Metric Spaces, 2da Edn, Ed Dover Publications, New York, 1983.         [ Links ]

[8] J. I. Mojica, C. Castellanos, S. Usma. y R. Álvarez, Libro Rojo de peces dulceacuícolas de Colombia, Ed Universidad Nacional de Colombia, Bogotá, 2002.         [ Links ]

[9] A. Calderer, Influencia de la temperatura y la salinidad sobre el crecimiento y consumo de oxígeno de la dorada (Sparus aurata L.), Ed Universidad Nacional de Colombia, Tesis de doctor en Ciencies Biologiques, Bogotá, 2001.         [ Links ]

[10] W. Holmes, y E. Donaldson, "Fisiología de los peces: Los compartimentos del cuerpo y la distribución de los electrolitos", Academic Press, vol. 1, pp. 1-89, 1969.         [ Links ]

[11] F. Beux, Da Efeito salinidade na Sobrevivencia de larvas de surubí ( Pseudoplatystoma corruscans ) (Agassiz, 1829) (Pisces: Pimelodidae), Technical report, XIII Congresso Brasileiro de Engenharia de Pesca-CONBEP, XIII, Porto Seguro -BA., 2003.         [ Links ]

[12] V. Stappen, Manual para la producción y uso de alimentos vivos para la acuicultura, Technical report, FAO Documento Técnico de Pesca. no. 361. Roma, XIII, pp. 107-123, 1996.         [ Links ]

[13] L. Beux, and E. Zaniboni-Filho, Influencia da baixa salinidade na Sobrevivencia de nauplios de Artemia sp, Technical report, Boletim do Instituto de Pesca, São Paulo, XIII, pp. 73-77, 2006.         [ Links ]

[14] J. Lu, and G. K. Bhattacharryya, "Some New Constructions of Bivariate Weibull Models", Annals of the Institute of Statistical Mathemati, vol. 43, no. 3, pp. 543-559, 1990.         [ Links ]

[15] E. W. Frees, J. F. Carriere, and E. Valdez, "Annuity valuation with dependent mortality", Journal of Risk and Insurance, vol. 63, pp. 231-261, 1996.         [ Links ]

[16] S. Yañez, H. Brango, M. Jaramillo, y C. Lopera., "Comparación entre riesgos competitivos vía estimador cópula-gráfico", Revista Colombiana de Estadística, vol. 34, no. 2, pp. 231-248, 2011.         [ Links ]