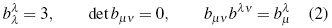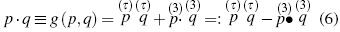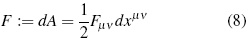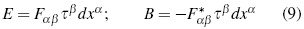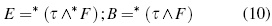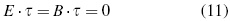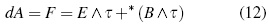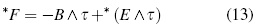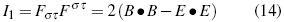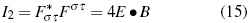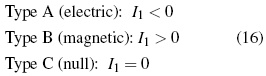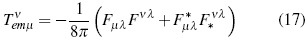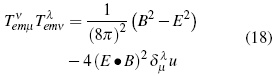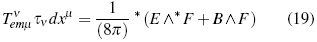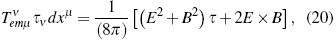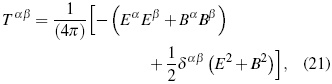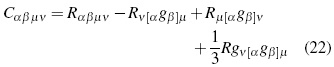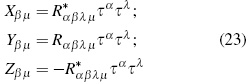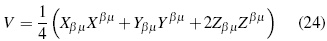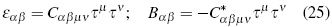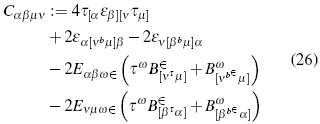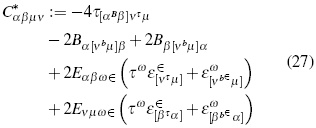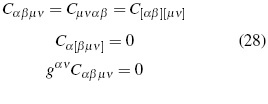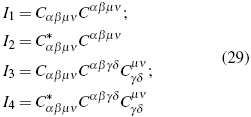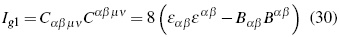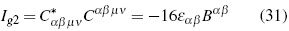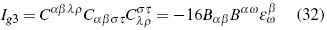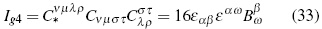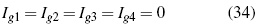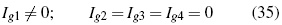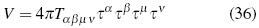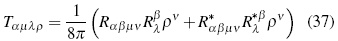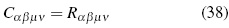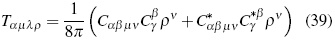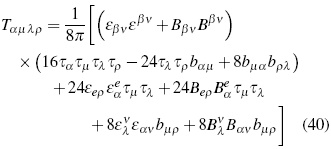New Analogies Between Electromagnetic and Gravitational Fields Through the Bel-Robinson Tensor

Nuevas analogías entre los campos electromagnético y gravitacional a través del tensor de Bel-Robinson

Ángel J. Chacón Velasco^a*
José A. Rizzo Sierra^b
Harold R. Rosas^c

^a Universidad Pedagógica y Tecnológica de Colombia (Uptc). Tunja, Colombia. Escuela de Física.
^* Autor de correspondencia: ajoschve@gmail.com
^b Universidad Industrial de Santander (UIS). Bucaramanga, Colombia. Escuela de Física.
^c Universidad Pedagógica y Tecnológica de Colombia (Uptc). Tunja, Colombia. Escuela de Física.

Recepción: 05-may-2014 Aceptación: 29-ene-2016

Abstract

Based on the 3+1 formalism by which is possible the formulation of an arbitrary reference frame within the General Relativity Theory, (GRT), we establish deep analogies between gravitational and electromagnetic fields. To achieve it, new gravitational invariants expressions from the Bel Robinson tensors, and through the Weyl's quasi-electric and quasi-magnetic field's tensors in gravitation, were obtained. Furthermore, some theoretical consequences on the development implications of those analogies are established and discussed within the context of the yet to be proved gravitational waves' experimental reality.

Key words: TGR's Interpretation, BR's or Superenergy Tensor, Gravitoelectromagnetic Tensor, Stress-Energy, Gravitational Waves.

Resumen

Basados en el formalism 3+1, con el cual es posible formular un sistema de referencia arbitrario en la Teoría General de la Relatividad TGR, establecemos profundas analogías entre los campos gravitacional y electromagnético. Para lograrlo se obtuvieron nuevas expresiones para los invariantes gravitacionales y del tensor de Bel Robinson a través de los campos de los tensores cuasi-eléctricos y cuasi-magnéticos de Weyl en gravitación. Adicionalmente, son brevemente discutidas algunas implicaciones teóricas de estas analogías en el contexto de la aún no verificada realidad experimental de las ondas gravitacionales.

Palabras clave: Interpretación de la TGR, Tensor de superenergía o BR, Tensor gravitoelectromagnético, Energía tensionada, Ondas gravitacionales.

1. Introduction

Since the formulation of the General Theory of Relativity (GTR) in 1916, as a relativistic theory of gravitation, several analogies have been established and discussed between gravitational and electromagnetic fields, frantically searching for perspectives of solution on the problem represented by the gravitational energy definition. This problem is closely related with that of gravitational waves, as well as the problem of gravity quantization, symmetries, and conservation laws, among other important problems which remain open in contemporary physics. In this article, emphasis is done on the theoretical significance of the analogy between GTR and electromagnetic theory.

In that spirit, Bel's tensor was introduced in the late 50's as an attempt to formulate within gravitational theory, what the energy-momentum tensor represents to electromagnetic theory [1,2]. The underlying idea consisted in taking the electromagnetic energy-momentum field tensor and attempting to successfully translate it into its gravitational counterparts by substituting Faraday's tensor for Riemann's. The result is a fourth order tensor first studied by Bel, which has mathematical properties similar compared to those of the electromagnetic energy-momentum field tensor. Now, when Riemann's tensor is replaced by Weyl's, BR's tensor is obtained. BR's tensor represents a different energy, often referred to as "super-energy", which continues to be an object of debate, due to the fact that there are no definite conclusions on its physical meaning, though consensus has been reached on the opinion it does not represent the gravitational field's energy, as well as on the one regarding the term "super-energy" as a hypothetical one [5, 8].

Consequently, one of the most remarkable theoretical aspects of GTR continues to be the difficulty to define an adequate concept of gravitational energy density. The origin of that difficulty lies on the equivalence principle, because any geometrophysical object representing gravitational energy-momentum, can be made to vanish by adequately choosing the reference frame employed. Such an object would not be a tensor but a pseudo-tensor and will evidently depend upon the reference frame selected. Several expressions attempting to describe gravitational energy have been proposed, but no general satisfactory formalism has emerged yet. (In other words, only formalisms for particular cases have been discussed) [16].

This is the general context in which the BR's tensor expression is proposed in this paper, and is developed by means of the electric and magnetic Weyl tensors [3] and 3+1 formalism [13, 9]. It should be noted that as a general context, it is of the most and actual importance in theoretical physics, since the existence of gravitational waves direct experimental proof, remains prospective, up to the present day [15].

2. Experimental

2.1. 3+1 Formalism

In our general relativistic approach and 3+1 formalism, a monad is a time-like vector field which is interpreted as a fourth-velocity field τ, of local observers equipped with all necessary measurement devices. A congruency of integral lines of that vector field, can be associated to the region of space-time where the reference frame is located (i. e., timelines of the particles forming the reference body).

In the region under consideration such monad is introduced as time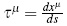 in addition to fourth dimentional metric g, with τ · τ =+1 as its normalization condition. Then the following symmetrical tensor is the projector under the local orthogonal subspace for τ:

With the properties:

As a result, b simultaneously plays both the role of projector and metric in this subspace. In addition, it is worthy of notice that this three-dimentional physical space defined by the reference frame, is non-holonomic when the τ-congruence is rotating [10].

On the other hand, in order to apply the 3+1 formalism in a way designed to serve our purposes, the projection for an arbitrary four-(co)vector q onto the monad is defined as the scalar:

Complementarily, the projection onto the threespace of the reference frame is defined as the four-dimensional (co)vector:

Hence, q then can be decomposed as:

Operating equivalently, it can be shown that:

With p · q = ∗[(τ ∧ p) ∧∗(τ ∧ q)]; notation introduced by Mitskievich [9]. Thus, equations (3) to (6) succinctly show how the 3+1 formalism allows the spatial and temporal splitting of physical magnitudes.

2.2. The Energy-Momentum Electromagnetic Field Tensor Trough 3+1 Formalism

The application of the 3+1 formalism requires the introduction of the language of differential forms, where the electromagnetic four-potential is represented by the 1-form:

Conversely, and the 2-form of the electromagnetic field strength is:

Therefore electric and magnetic fields can be defined as follows [10, 15]:

Which have the equivalent expressions:

* being the Hodge operator. Let us now notice that E and B generated in this fashion, are very simple and applicable definitions for all reference frames and gravitational fields of the electric field strength and magnetic displacement vector, both orthogonal to τ:

In this way, definitions in equations (9) and (10) imply the following decomposition:

And its dual:

The electromagnetic invariants can then be expressed as follows:

Magnitudes (14) and (15) are invariants in any reference frame and gravitational field. Upon that observation, a very simple classification system in terms of electric, magnetic and null field types has been established [6], [12]:

Invariant I₂, or more precisely a pseudo-invariant, allows the setting up of an additional classification; I₂ = 0 as pure and I₂ =0 as impure electric or magnetic fields respectively. Being the previous an algebraic classification, the type of electromagnetic field can vary from one point to another.

Now, to continue advancing along the main line of this paper, an important object in electromagnetic theory, is the energy-momentum electromagnetic field tensor -which defines its energy density-, given by [6], [9]:

Which satisfies T ^ν_emν Ξ 0. In addition, from T ^ν_emν it can be obtained an identity in accordance with Wheeler's Geometrodynamics [14]:

Finally, in order to express the energy-momentum electromagnetic field tensor using observable magnitudes, the 1-form T ^ν_emµ τν dx^µ must be considered. It can be found that:

From which it can be obtained:

completely in agreement with usual interpretation of the first term; along the physical time of the reference frame (τ), as the electromagnetic energy density, and of the second one; in the three-space of the reference frame, as the electromagnetic energy flux density (Poynting's vector magnitude).

It also can be useful for the purposes of this paper the following classical 3-dimensional electromagnetic stress tensor expression [7]:

because of its purely spatial meaning.

2.3. Weyl's Tensor Trough 3+1 Formalism

It is known that in the space-time vacuum (R_αβ = 0 and R = 0) Weyl's tensor behaves as the curvature tensor. In these conditions Weyl's tensor is conformally defined as follows:

Hence, C_αβµν= R_αβµν . Historically, while researching the problem of radiation within TGR, the first attempt to split the curvature tensor in the sense of a reference frame decomposition was performed by Matte in 1953, and further developed by Zakharov in 1973 [15]. Afterward, Bel and Robinson [11] proposed a local energy density definition for the gravitational field trough the following tensors in monad terms:

Resulting the scalar:

Where it can be shown that if R_αβλµ ≠ = 0; then V > 0 in all circumstances.

In analogy with electromagnetic theory's electric and magnetic fields, the following notation -using the 3+1 representation as well-was introduced [16]:

Where ε_αβ, and B_αβ are symmetric and traceless. These tensors are called electric and magnetic Weyl tensors (also called quasi-electric and quasimagnetic fields or tensor fields), respectively, and play the role of electric and magnetic tension in the electromagnetic theory.

Therefore, also in close analogy with what happens to the energy-momentum electromagnetic field tensor, we propose that Weyl's tensor can be defined using the quasi-electric and quasi-magnetic fields [4]:

Aided by the Hodge operator (∗), its dual can be obtained:

Where 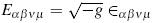is the Levi-Civita's tensor. Weyl's tensor defined this way has the same symmetry properties of Riemann's tensor, i. e.:

Brackets [...] meaning anti-symmetry properties for those indexes contained by them.

3. Invariants and Quasi-Electric/magnetic Fields

Now, within TGR's context, the system of invariants for Weyl's tensor is composed of fourteen elements [10]. Taking into account the correspondence between Weyl's tensor and Riemann's in space-time vacuum, there are only four relevant independent invariants. They are:

The result of calculating these invariants with Weyl's tensor written in terms of quasi-electric and quasimagnetic fields is [4]:

First invariant:

This result is very similar to the first electromagnetic invariant (14).

Second invariant:

In its turn being very similar to the second electromagnetic invariant (15).

Third invariant:

Fourth invariant:

Is important to note that these last two invariants do not possess electromagnetic counterparts to be compared. The theoretical relevance of invariants (30) to (33) consists mainly, in them being capable of expressing Bel's second criterion for the existence of gravitational waves, since:

For any isotropic gravitational field [15].

In this context we can propose, similarly as done in (16), some necessary conditions -though probably not sufficient- for the classification of quasi-electric and quasi-magnetic fields:

Where if I_g1 > 0, the field will have quasi-electric nature; and if I_g1 < 0, the field will have quasi-magnetic nature [4].

3.1. BR's "Super-Energy" Tensor Through 3+1 Formalism

Replacing (23) into (24) for a vacuum spacetime it is obtained the following scalar:

Magnitude T_αβµν being called BR's tensor or "superenergy" tensor [5], [8], referring to a fourth rank tensor with the form:

Comparing (37) with (17) the analogy between both expressions becomes noticeable, despite their difference in tensorial rank. The role played by the field intensity in expression (17) is in equation (37) performed by Riemman's space-time curvature tensor (relativistic intensity). Like the energy-momentum electromagnetic field tensor, the "super-energy" ten-sor is symmetric for all indexes and its contractions. For instance, also in vacuum space-time conditions, it can be shown that Tα^αµν = 0. Finally, in absence of non-gravitational fields, the covariant conservation law T^µνλρ ;ρ = 0 is observed as a consequence of Bianchi's identities and the vanishing of Einstein's tensor.

Always in vacuum space-time conditions, where Weyl's tensor behaves as Riemann's, it can be proposed that:

Hence, BR's tensor becomes the following tensor:

Now, a new explicit expression for this last tensor can be obtained by writing Weyl's tensor in terms of quasi-electric and quasi-magnetic fields. Operating in the same way previously used to find the invariants, the following expression is proposed as a new and original expression for BR's tensor (another name could be posited for it):

Now, regarding its physical meaning, in first instance, (ε_βνε^βν + B_βν B^βν) the scalar could be called local gravitational "super-energy density". Is clear that the third, sixth, and seventh terms would allow us to identify a gravitational analogue to the electromagnetic stress tensor, which could be called the "gravitational stress tensor". Remaining terms would then represent an analogue of the electromagnetic energy flux, which could be in its turn called -rather awkwardly, we are afraid-"gravitational super-energy flux". Let us mention again that, although interesting and colorful, in all these cases the referred analogies are somewhat liberal, considering we are comparing quantities with different tensorial ranks. All this adding to the point we would want to stress with this article: Given the fact that the existence of gravitational waves has not been directly proven yet, new expressions of BR's tensor such as the proposed here, as well as all the sort of related subjects on these matters appearing in articles similar to this one should be examined and discussed thoroughly, since there is the possibility that usual interpretations on the physical meaning of main TGR's entities could have been over optimistic.

With that we mean that rather than trying to en-force the parallelism between TGR and electromagnetic theory, as an obvious and settled argument in favor of the existence of gravitational waves, perhaps it could be interesting to inquire on its differences (non analogical properties). Even in the case that the existence of gravitational waves became undoubtedly proven in the near future, considering the mathematical differences among them, from a theoretical viewpoint, it would be clear that the analogy is consistent and fruitful only to a certain extent, and that the differences in the sake of theoretical openness and completion need not to be put under the carpet, but, on the contrary, assimilated in a proper fashion (developing interpretations for them).

In other words, when choosing at all costs to interpret TGR's entities in a fashion compatible with the existence of gravitational waves, in the sense of electromagnetic theory, a wealth of prospective realities could be bluntly dismissed, i. e., related to interpretations of TGR's entities which could open up new and interesting theoretical perspectives if properly inquired. On these lines, a new expression for BR's tensor such as the one proposed here, helps to bring the subject out of the shadows, since the analogy between TGR and electromagnetic theory via BR's tensor, is only straightforward for the case of the equally troublesome local gravitational "superenergy density and "gravitational stress tensor". Additional analogies are even more troublesome, as shown.

4. Conclusions

• Original expressions for BR's and Weyl's tensors in terms of quasi-electric and quasimagnetic fields were proposed (40).


• Using the 3+1 formalism, explicit expressions for the fundamental invariants (29) of gravitation in a curved space, were found by means of a Riemann's tensor decomposition, through the conformal Weyl's tensor via quasi-electric and quasi-magnetic fields (25).


• The new expression for BR's tensor can con-tribute to the clarification of the "super-energy" concept meaning, within the actual context of TGR. From the perspective of theoretical criteria for the existence of gravitational waves, Bel's second criterion is reaffirmed by the present treatment, relating quasi-electric ( ε_αβ ) and quasi-magnetic ( B_αβ ) tensors with the prospective reality of gravitational radiation, in close analogy to electromagnetism. Moreover, an alternative classification for those fields is proposed, remarking the elegant isomorphism between electromagnetism and gravitation. Analogies between gravitational and electromagnetic fields and their invariants, became noticeable when comparing the "super-energy" tensor with the energy-momentum electromagnetic field tensor. Interestingly but not unexpectedly, the "super-energy" tensor exhibits all physical quantities as composed by separated quasi-electric and quasi-magnetic elements. The scalar (ε_βν ε^βν + B_βν B^βν) is identified as local gravitational "super-energy density". Third, sixth, and seventh terms of "superenergy" tensor are associated to a "gravitational stress tensor". Remaining terms can be imagined to represent a "gravitational super-energy flux". These analogies are not as straightforward as desirable, because of the gravitational field's complex nature and other circumstances.


• The analogy between TGR and electromagnetic theory via BR's tensor and similar procedures, show to us that from a purely theoretical (mathematical-physics) standpoint, analogies can be reasonably argumentative; but from a science viewpoint philosophy, the initiative could be considered exclusive and limiting towards the true theoretical possibilities of TGR's mathematical formalism.

Acknowledgments

We would like to specially thank Prof. N. V. Mitskievich for the impact, deepness and availability of his work, as well as for his warm humanity.

References

[1] L. Bel. Sur la radiation gravitationelle, C R Acad. Sci., Paris, no. 247, pp. 1094-6. 1958.         [ Links ]

[2] L. Bel. Introduction d'un tenseur de quatrieme ordre, CR Acad. Sci., 1958.         [ Links ]

[3] W. B. Bonnor. "The Electric and Magnetic Weyl Tensors". Class, Quantum Grav, no. 12, pp. 499-502. 1995.         [ Links ]

[4] A. J. Chacón. "Campos cuasimagnéticos gravitacionales y su analogía con el electromagnetismo", Revista Integración UIS, Colombia, vol. 2, n.^°2, 1993.         [ Links ]

[5] J. Garecki. "Some Remarks on the BelRobinson's Tensor", preprint gr-qc/0003006. 2007.         [ Links ]

[6] L. D. Landau, and E. M. Lifshitz. Classical Field Theory. Reading, Mass.: Addison-Wesley. 1971.         [ Links ]

[7] A. P. Lightman, W. H. Press, R. H. Price. Teukolsky. Problem book in relativity and gravitation. Princeton, N. J.: Princeton University Press. 1975.         [ Links ]

[8] B. Mashhoon, J. McClune, H. Quevedo. "Gravitational Superenergy Tensor". Phys. Lett., A231, pp. 47-51. 1997.         [ Links ]

[9] N. V. Mitskievich. "Relativistic physics in arbitrary reference frames", preprint gr-qc/9606051 v1 17, Jun 1996.         [ Links ]

[10] N. V. Mitskievich, A. P. Efremov, A. I. Nesterov. Dynamics of Fields in General Relativity. Moscow: Energoatomizdat. In Russian. 1985.         [ Links ]

[11] J. M. M. Senovilla, in Gravitation and Relativity in General, Proccedings of the Spanish Relativity Meeting in Honour of the 65^th Birthday of L. Bel, eds. J. Martín, E. Ruiz, F. Atrio and Molina. World Scientific, Singapore, 1999, pp. 175-182 (gr-qc/9901019).         [ Links ]

[12] J. L. Synge. Relativity: The General Theory, Amsterdam: North-Holland. 1960.         [ Links ]

[13] Y. S. Vladimirov. Reference Frames in Gravitation Theory., Moscow: Energoatomizdat. In Russian. 1982.         [ Links ]

[14] J. A. Wheeler. Geometrodynamics. New York: Academic Press. 1962.         [ Links ]

[15] V. D. Zakharov. Gravitational Waves in Einstein's Theory. New York: Halsted Press. 1973.         [ Links ]

[16] A. L. Zel'manov, and Agakov, V. G. Elements of General Theory of Relativity. Moscow: Nauka. In Russian. 1989.         [ Links ]