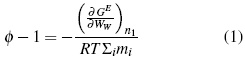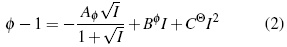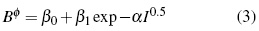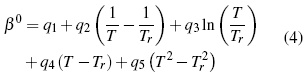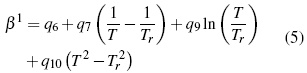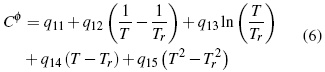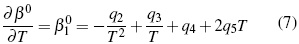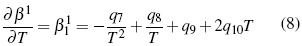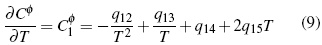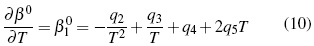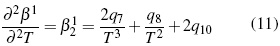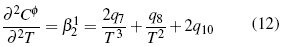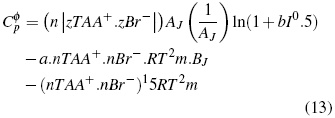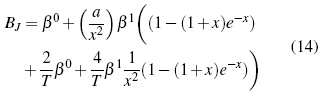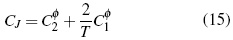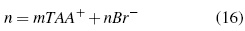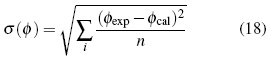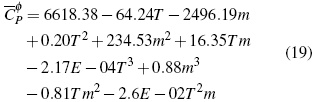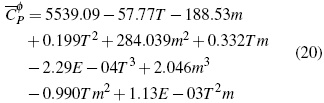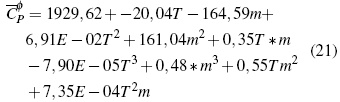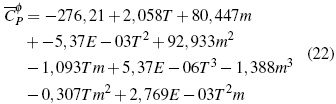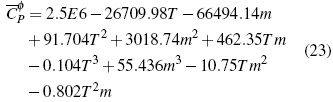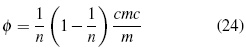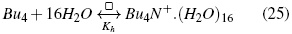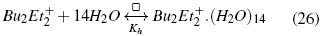Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia en Desarrollo
Print version ISSN 0121-7488
Ciencia en Desarrollo vol.7 no.2 Tunja July/Dec. 2016
Predicción de la capacidad calorífica molal aparente y concentración micelar crítica (cmc) en soluciones acuosas de amonio cuaternario en función de temperatura (283.15 a 298.15) K.
Prediction of Molal Apparent Heat Capacity and Critical Micellar Concentration (cmc) of Aqueous Solutions of Quaternary Ammonium Salts at Temperature (283.15 to 298.15) K.
Eliseo Amado-Gonzáleza*
Alfonso Quijano-Parrab
Luis H. Blancoc
a Grupo de Energía, transformación química y medio ambiente. Laboratorio de Biocombustibles. Universidad de Pamplona, Norte de Santander, Colombia.
* Autor de correspondencia: eamadogon@gmail.com.
b Grupo de Investigación en Química. Laboratorio de Control de Calidad Universidad de Pamplona. Norte de Santander, Colombia.
c Laboratorio de Investigaciones Básicas, LIB. Universidad Nacional de Colombia. Q.E.P.D. Colombia.
Recepción: 16-feb-2016 Aceptación: 27-may-2016
Resumen
El objetivo de la investigación es predecir la capacidad calorífica molal aparente (Cφp) de las soluciones de líquidos iónicos de amonio cuaternario de Bu4NBr, sec-Bu4 NBr, iso-Bu4NBr, BuEt3NBr y Bu2Et2NBr mediante la ecuación de Pitzer modificada en función de temperatura (283.15 a 298.15) K en el rango de concentración (0.09 a 1.1) m. Se calculan las funciones para la capacidad calorífica mediante la metodología de superficie de respuesta. La concentración micelar crítica para las sales es calculada alrededor de (0.4 a 0.45) m a 298.15 K mediante el modelo de Desnoyers. Se encuentra que los números de agregación para la solvatación (n) varían entre 11 a 16 a 298. 15 K. Se proponen las relaciones estequiométricas de solvatación para cada sal.
Palabras clave: ecuación de Pitzer modificado, coeficiente osmótico, capacidad calorífica molal aparente, sales de amonio cuaternario.
Abstract
The aim of the research is to predict the apparent heat capacity (Cφp ) of aqueous solutions of quaternary ammonium liquid ionics of Bu4NBr, sec-Bu4NBr, iso-Bu4NBr, and Bu2Et2NBr BuEt3NBr by Pitzer equation modified depending on temperature (283.15 to 298.15) K at concentration range (0.09 to 1.1) m. The functions of the heat capacity are calculated by surface response methodology. The critical micelle concentration for salts was found around (0.4 to 0.45) 298.15 K m by Desnoyers model. The numbers of aggregation for solvation (n) ranging from 11-16 to 298. 15 K. The stoichiometric ratios of solvation for each salt are proposed.
Key words: Pitzer Semi-Empirical Equation Modified, Osmotic Coefficient, Apparent Molal Calorific Capacity, Tetra-Alkyl-Ammonium Quaternary Salts.
1. Introducción
Las líquidos iónicos tienen amplias posibilidades de aplicación en diferentes procesos industriales desde metalurgia, extracción de solventes, absorción química, procesos de desalinización, procesos biológicos, geoquímica y química verde [1]. Los líquidos iónicos son sales fundidas a temperatura ambiente o menores de 100 °C. Los líquidos iónicos son conocidos como "solventes diseñadores", ya que sus propiedades físicas y químicas pueden ser ajustadas o manipuladas usando diferentes combinaciones entre aniones y cationes. Las sales de amonio cuaternario son una clase muy interesante de líquidos iónicos con un átomo de nitrógeno en el centro y cuatro radicales alrededor [2]. Las cuales presentan puntos de fusión normalmente mayores de 100 °C.
En la aproximación semi-empírica de coeficientes viriales de Pitzer [3,4] se pueden describir los sistemas de forma aceptable las propiedades termodinámicas de electrólitos hasta valores de fuerza iónica cercanos a 6 mol.kg −1. La modificación realizada por Clegg para este modelo, permite utilizarlo con electrolitos de cualquier tipo de carga asimétrica y en presencia de especias neutras y sin restricción en el valor de la fuerza iónica [5].
En el presente trabajo se utilizan los datos de coeficientes osmóticos de líquidos iónicos soluciones acuosas de sales de tetra-alquil-amonio cuaternario (TAABr) en función de temperatura para el cálculo de la capacidad calorífica molal aparente (Cφp ). Con los datos de coeficientes osmóticos se calculan la concentración micelar crítica (cmc) y el número de agregación (n). Las ecuaciones de (Cφp ) se calculan mediante la metodología de superficie para cada TAABr en solución acuosa. La concentración micelar crítica (cmc) y el número de agregación se utilizan para explicar los fenómenos de solvatación de las sales de TAABr.
2. Metodología
2.1. Datos de Coeficientes osmóticos de las soluciones de TAABr
Datos de literatura [6-9] de coeficientes osmóticos de soluciones acuosas de n-Bu4NBr, secBu4NBr, iso-Bu4NBr, Bu2Et2NBr and BueEt3NBr en función de temperatura se utilizan para calcular las capacidades caloríficas, la concentración micelar crítica (cmc) y los números de agregación (n).
2.2. Calculo de la propiedad molal aparente
La energía libre (ΔGE) está relacionadas con el coeficiente osmótico (φ) según las ecuaciones (1) y (2).
El parámetro de Debye-Hückel, Aφ , es 0.3821 (kg/mol)0.5 a 283.15 K, 0.3882 (kg/mol)0.5 a 288.15 K, 0.3915 (kg/mol)0.5 a 298.15 K y 0.3949 (kg/mol)0.5 a 303.15 K. R es la contante de los gases, T es la temperatura (K), m es la molalidad, I la fuerza iónica, y α es un parámetro ajustable [10].
Los parámetros desde q1 hasta q15 en función de temperatura son calculados por el método iteractivo.. Los aspectos teóricos pueden ser consultados en literatura [11, 12].
Donde Tr es la temperatura de referencia a 298.15 K. A partir de las ecuaciones (8, 9) se calcula la entalpía molal aparente (L↑φ)
A partir de las ecuaciones (11, 12) se calcula (Cφp ).
Donde el (Cφp ) se calcula:
Donde TAA+ es catión, Br− anión y z+ y z− las cargas respectivas de los iones.
Donde,
Donde los parámetros, Aφ ,y AJ son pendientes límites de Pitzer-Debye-Hückel para coeficiente osmótico y la capacidad calorífica resumidos en literatura [13]. Los parámetros dependientes de temperatura son β(0), β(1) y Cφ.
El coeficientes osmótico calculado puede ser obtenido con un error promedio absoluto de 0.5% (desviación estándar de σ(φ)= 0.04) para las soluciones de haluros de amonio cuaternario en el rango de concentración (0.03 a 2.5) mol.kg−1 a 298.15 K. La desviación estándar es calculada entre el valor experimental y el valor calculado del coeficiente osmótico, ecuación (18):
3. Resultados
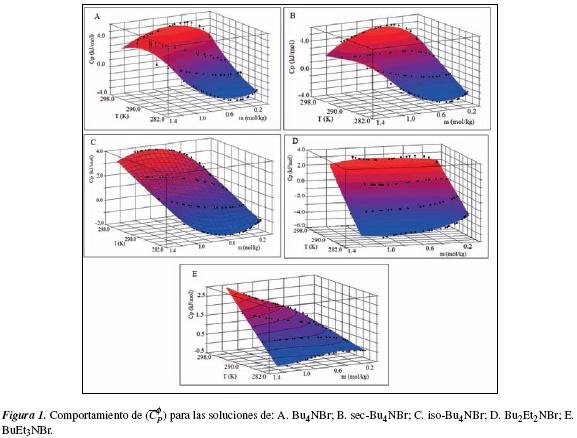
En la figura 1A se analiza el comportamiento de (Cφp ) en función de la m y T mediante la metodología de superficie (figura 1). Se calcula ecuación (19) para las soluciones acuosas de Bu4NBr con un error estándar estimado de 0.11 J/mol K para un nivel de confianza del 99%.
El comportamiento de (Cφp ) para las soluciones de sec-Bu4NBr permite calcular la ecuación (20) con un error estándar de 0.087 J/mol K en un nivel de confianza del 99.9% (figura 1B).
En la figura 1C se observa el comportamiento de la superficie de respuesta para las soluciones de iso-Bu4NBr donde (Cφp ) en función de temperatura y molalidad permite obtener la ecuación (21) con un error estándar de 0,069 J/mol K en un nivel de confianza del 99.9%:
El análisis de superficie de respuesta para las soluciones de Bu2Et2NBr de la figura 1D se obtuvo la ecuación (22):
La ecuación (22) es calculada con un error están-dar estimado es de 0.167 (J/mol K) para un nivel de confianza del 99%.
El análisis de la superficie de respuesta para las soluciones acuosas de BuEt3NBr en la figura 1E permite obtener la ecuación (23) calculada con un error estándar estimado de 0.07 J/molK en un nivel de confianza del 99.9%:
Estudios calorimétricos de soluciones acuosas de TAABr por medidas directas de cambios de temperatura en proceso de disolución se han desarrollado en sales de Bu4NBr [14-17]; en iso-Bu4NBr y secBu4NBr [17] en zonas en concentración diluida.
Para calcular la concentración micelar crítica (cmc) y el número de agregación de moléculas de agua (n) se utiliza el modelo de separación de seudo - fase [18] según la ecuación (24). Donde a partir de los datos de coeficientes osmóticos se realizan los cálculos de cmc y n:
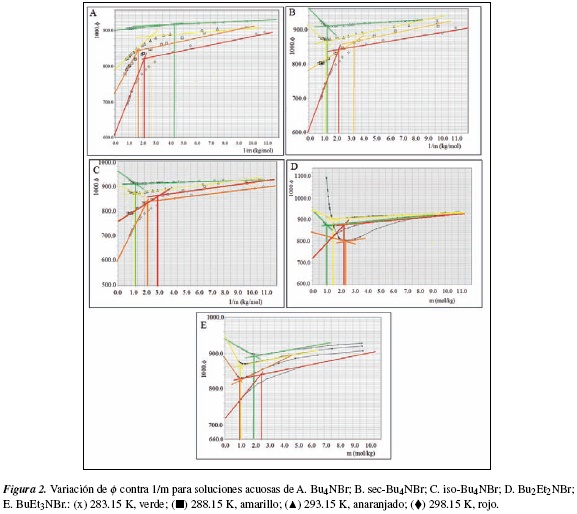
En la figura 2A se observa el comportamiento de φ, para las soluciones acuosas de Bu4NBr en función de la temperatura donde se observa que a 293.15 K a 298.15 K existiría una cmc. La cmc se encuentra a 298.15 K esta alrededor de 0.4 m y disminuye hasta 0.2 m para 283.15 K. De acuerdo con los resultados, n, el número de agregación, varía entre 11 a 16 a 298.15 K.
En la figura 2B, se obtiene que el número de agregación, n varía entre 16 a 298.15 K a 11 para 283.15 K. Estos resultados sugieren para las soluciones de Bu4NBr y sec-Bu4NBr, que el número de moléculas de agua que estaría inter actuando con el catión aumenta con la temperatura. La cmc calculada para las soluciones de sec-Bu4NBr, se encuentra alrededor de 0.45 m a 298.15 K, de 0.71 m a 283.15 K y 0.28 m a 293.15 K. Es decir, no es posible establecer una relación lineal entre la variación de cmc y la variación de la temperatura.
En el análisis de la figura 2C para las soluciones de iso-Bu4NBr, se encuentra una cmc de 0,67 m a 283,15 K y 288,15 K mientras que n varía entre 11 y 10,4 respectivamente. A 298,15 K la cmc está a 0,45 m para n 16.
En la figura 2D se presenta el análisis para las soluciones acuosas de Bu2Et2NBr donde se encuentra que cmc varía entre 0.1 a 283.15 K y 0.4 m a 298.15 K. Mientras que n, varía de 10.4 a 293.15 K hasta 14 a 298.15 K.
Los resultados obtenidos en la figura 2E muestran que cmc para las soluciones de BuEt3NBr a 288,15 K y 293,15 K es de 0,90 m y disminuye hasta 0,4 m a 298,15 K. El valor de n varía de 10 a 283,15 K hasta 14 a 298,15 K.
4. Discusión
De acuerdo con Ben-Naim [19] existe una relación entre las moléculas de solvente y las respectivas moléculas de la sal de TAAX ( X = haluro), tendría un efecto disruptor, es decir, rompe la estructura del agua, y que las interacciones soluto-soluto serían mayores en la medida en que disminuye la temperatura. Las sales de TAAX se pueden clasificar al disociarse en soluciones acuosas como disruptoras, si se caracterizan por la baja densidad superficial de carga y su alto volumen [20]. En el caso de las soluciones de Bu4NBr y sus isómeros iso-Bu4NBr y sec-Bu4NBr, se esperaría que debido a su geometría en comparación con la geometría de BuEt3NBr y Bu2Et2NBr el valor de n disminuyera con la temperatura, es decir, que la afinidad agua-soluto fuera menor.
Sin embargo, el efecto disruptor del catión de TAA+ debe variar con el tamaño y las condiciones externas a las cuales está sometido, es decir, la variación de temperatura y/o la constante dieléctrica del solvente [21]. De otra parte, al analizar los datos de n y cmc, se podría considerar que las sales de TAAX presentarían mezclas de distinto tipo de moléculas de agua, donde la constante dieléctrica dependería de si están asociadas, donde las interacciones de hidrógeno cumplirían una función predominante [22]. Por tanto, aunque inicialmente el catión produciría una ruptura de la estructura del agua, dentro del proceso de ubicación del catión, esto estaría produciendo un ordenamiento distinto, que si se compara con la estructura del agua en su seno, podría mayor. Por tanto, se esperaría que los cationes de TAA+ con las cadenas más largas y preferiblemente lineales se ubicaran mejor que aquellos cationes con cadenas ramificadas o con cadenas cortas. En el caso del Bu2Et2NBr, su comportamiento podría deberse a algún tipo de impedimento entre los dos tipos de cadena de ramificada.
Este resultado interpretado con la hipótesis de la presencia de una estructura altamente ordenada. Aparentemente las cadenas no ramificadas del radical butilo favorecen las interacciones con las moléculas de agua. De acuerdo Slusher y Cummings [23], los hidrógenos de las cadenas de alquilo del Bu4NBr se orientan con el polo negativo del oxígeno de la molécula de agua. Es decir, podría existir una relación dentro el comportamiento de las curvas de capacidad calorífica y las cmc.
Los números de agregación sugieren que para los isómeros de butilo el valor va desde 11 hasta 16 a 298,15 K. Los resultados obtenidos son consistentes con los obtenidos por Ben-Naim [19] en su estudio de la correlación soluto-soluto, donde se encontró que el rango de correlación soluto -soluto es mayor a bajas temperaturas (mayores (Cφp ). En la ecuación (26) se utiliza n para presentar el modelo de solvatación para el Bu4N+ que resultaría de las interacciones de hidrógeno y a las interacciones solvofóbicas entre la parte apolar del catión y las moléculas de agua [24].
Donde Kh es la constante de hidratación. De acuerdo con Turner y Soper [25] el efecto de un so-luto del tipo TAA+ debe ser formador de estructura. Fenómeno observado a baja temperatura, es decir, la cadena alquílica estabiliza la red de moléculas de agua a su alrededor al incrementar la energía de las interacciones de hidrógeno. Por tanto, los efectos sobre la estructura del agua debida tanto a la disminución de la temperatura como al tamaño del catión orgánico se reforzarían mutuamente.
Los números de agregación, n, obtenidos par las soluciones de Bu2Et2NBr y BuEt3NBr que varían entre 10 y 14 a 298,15 K sugiere que estos solutos con estructuras ramificadas no simétricas tendrían menores posibilidades de asociarse con moléculas de agua.
Se encuentra que al disminuir la temperatura desde 298.15 K a 283.15 K, cmc disminuye de 0.4 m a 0.1 m. Mientras que el valor de n disminuye de 14 a 10 moléculas de agua.
5. Conclusiones
La modelación de los coeficientes osmóticos de soluciones acuosas de TAABr con el modelo modificado de Pitzer permitió predecir 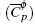 . Se utilizó la metodología de superficie de respuesta para evaluar las ecuaciones de la capacidad calorífica para cada TAABr en solución acuosa en función de temperatura.
. Se utilizó la metodología de superficie de respuesta para evaluar las ecuaciones de la capacidad calorífica para cada TAABr en solución acuosa en función de temperatura.
La cmc calculada para los isómeros de butilo alrededor de 0,4 m a 0,45 m a 298.15 K. Los números de agregación, n, obtenidos son constantes para los isómeros de butilo de 11 a 16 para 298,15 K. Mientras que disminuye de 10 a 14 para las sales de Bu2Et2NBr y BuEt3NBr.
Se utilizan los valores de n para proponer las ecuaciones estequiométricas de solvatación de acuerdo a los resultados obtenidos de número de agregación, n, donde la Kh, implicaría la relación entre moléculas de agua libre con mayor energía, y moléculas de agua asociada con menor energía.
Referencias
[1] Olivier-Bourbigou H, Magna L. "Ionic Liquids: perspectives for organic and catalytic reactions". J. Mol.Catal. A 182-183, pp 419-437, 2002. [ Links ]
[2] Belvéze L, Brennecke J, Stadtherr M. "Modeling of Activity Coefficients of Aqueous Solutions of Quaternary Ammonium Salts with the Electrolyte-NRTL Equation". Ind. Eng. Chem. Res.43, pp 815-825, 2004 [ Links ]
[3] Pitzer K.S. "Thermodynamics of electrolytes. I. Theoretical basis and general equations". J. Phys. Chem. 77, pp 268-277,1973. [ Links ]
[4] Pitzer K, Mayorga G. "Thermodynamics of Electrolytes, II. Activity and osmotic coefficients with one or both ions univalent". J. Phys. Chem. 77, pp 2300-2308, 1973. [ Links ]
[5] Clegg S, Pitzer K. "Thermodynamics of multicomponent, miscible, ionic solutions: Generalized equations for symmetrical electrolytes". J. Phys. Chem. 96, pp 3513-3520, 1992. [ Links ]
[6] Amado-González E, Blanco L H. "Isopiestic determination of the osmotic and activity coefficients of dilute aqueous solutions of symmetrical and unsymmetrical quaternary ammonium bromides with a new isopiestic cell at 298.15K". Fluid Phase Equil. 233, pp 230-233, 2005. [ Links ]
[7] Amado-González E, Blanco L H. "Osmotic and activity coefficients of dilute aqueous solutions of symmetrical and unsymmetrical quaternary ammonium bromides at 293.15K". Fluid Phase Equil. 243, pp 166-170, 2006. [ Links ]
[8] Amado-González E, Blanco L H. "Isopiestic Determination of the Osmotic and Activity coefficients of Aqueous Solutions of Symmetrical and Unsymmetrical Quaternary Ammonium Bromides at T (283.15 and 288.15) K". J. Chem. Eng. Data, 54 (9), pp 2696-2700, 2009. [ Links ]
[9] Amado-González E, Blanco L H. "Aplicación del modelo de interacción iónica de Pitzer a coeficientes osmóticos de soluciones de KCl en función de la temperatura". Bistua, 2 (1), pp 31-46, 2004. [ Links ]
[10] Pitzer K. "Activity Coefficients in Electrolyte Solutions". CRC Press. Boca Raton, 1991. [ Links ]
[11] Clegg S, Pitzer K."Thermodynamics of multicomponent, miscible, ionic solutions: Generalized equations for symmetrical electrolytes". J. Phys. Chem. 96, pp 3513-3520, 1992. [ Links ]
[12] Pitzer K. "Thermodynamics of electrolytes. I. Theoretical basis and general equations". J. Phys. Chem. 77, pp 268-277, 1973. [ Links ]
[13] Pitzer K, Mayorga G. "Thermodynamics of Electrolytes, II. Activity and osmotic coefficients with one or both ions univalent". J. Phys. Chem. 77 (19), pp 2300-2308, 1973. [ Links ]
[14] Krishnan C V, Friedman H L. "Enthalpies of Alkylammonium in water, heavy water, propylene carbonate, and dimethyl sulfoxide". J. Phys. Chem. 74 (22), pp 3900-3907, 1970. [ Links ]
[15] Visser C, Somsen G. "Hydrophobic interactions in mixtures of N, N-dimethyl formamide and water. Model calculations and enthalpies of solution". J. Phys. Chem. 78 (2), pp 1719-1722, 1974. [ Links ]
[16] Korolev V, Smirnova N, Kustov A. "Temperature dependence of the interaction between two hydrophobic solutes: a calorimetric study". Thermochim. Act. 427 (1-2), pp 43 -50, 2005. [ Links ]
[17] Blanco L H, Salamanca Y P, Vargas E F. "Heats of solution in water of salts of the type R4NBr and R2R'2NBr". J. Therm. Anal. Calorim. 92 (3), pp 683-686, 2008. [ Links ]
[18] Desnoyers J E, Caron G, Delisi R, Roberts D, Roux A, Perron G." Thermodynamic properties of alkyldimethylamine oxides in water. Application of a mass-action model for micellization". J. Phys. Chem, 87, pp 1397-1406, 1983. [ Links ]
[19] Ben-Naim A."One-dimensional model for water and aqueous solutions. IV. A study of hydrophobic interactions". J. Chem. Phys. 128 (10), 2008; doi.org/10.1063/1.2818051 pp 104506.g. [ Links ]
[20] Steigman J, Sussman D. Acid-base reactions in concentrated aqueous quaternary ammonium salt solutions. I. Strong acids and bases, carboxylic acids, amines, and phenol. J. Am. Chem. Soc. 89 (25), pp 6400-6406, 1967. [ Links ]
[21] Kežic B, Mazighi R, Perera A. "A model for molecular emulsions: Water and "weak water" mixtures". Physica A: Stat. Mechan. Appli. 392 (4), pp 567-582, 2013. [ Links ]
[22] Drain M, Gentemann S, Roberts J, Nelson N, Medforth C, Jia S, Simpson M, Smith K, Fajer J, Shelnutt J, Holten D. "Picosecond to Microsecond Photodynamics of a Nonplanar Nickel Porphyrin: Solvent Dielectric and Temperature Effects". J. Am. Chem. Soc. 120 (15), pp 3781-3791, 1998. [ Links ]
[23] Slusher J, Cummings P. "Molecular Simulation Study of Tetraalkylammonium Halides. 1. Solvation Structure and Hydrogen Bonding in Aqueous Solutions". J. Phys. Chem, 101, pp 3818-3828, 1997. [ Links ]
[24] El Seoud, O. "Understanding solvation". En: Pure Appl. Chem. 81 (4), 2009, pp 697-707. doi:10.1351/PAC-CON-08-09-27. [ Links ]
[25] Turner J, Soper A. "The effect of apolar solutes on water structure: Alcohols and tetraalkylammonium ions", J. Chem. Phys. 101, 1994, pp 6116. doi.org/10.1063/1.467327. [ Links ]