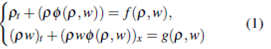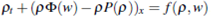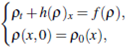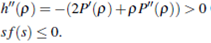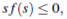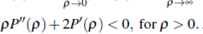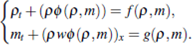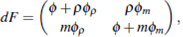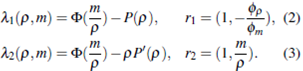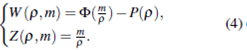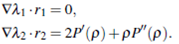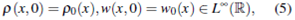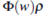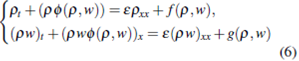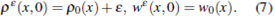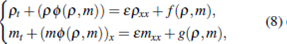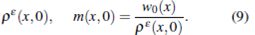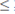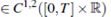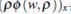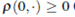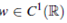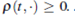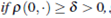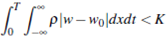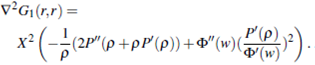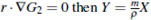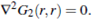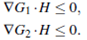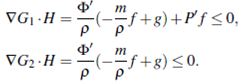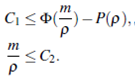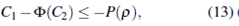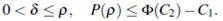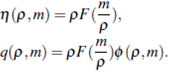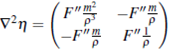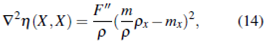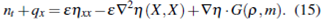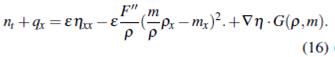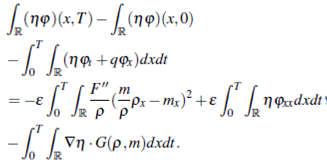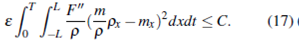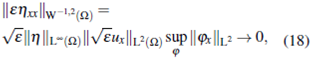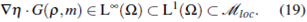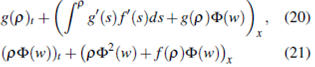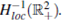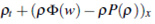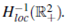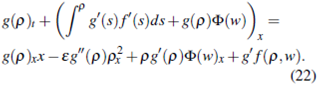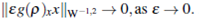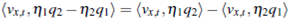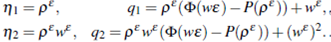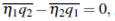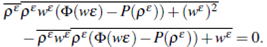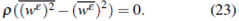1 Introduction
Many of the natural phenomena are modeled by partial differential equations. Some of the most common partial differential equations are the wave equation, the heat equation, the Schrõndinger equation and KdV equation. In this type of problems it is interesting to study the existence and uniqueness of solutions, which in many cases is not an easy task. For example, in the review article 1 the author studies the existence and uniqueness of solutions for non-linear Schrõndinger equation. However, in the hyperbolic equations the existence and uniqueness of solutions are a open problems. The goal this paper show the existence of solutions for a hyperbolic system of conservation laws. We consider the balanced non-symmetric system
where 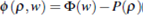 ,
, 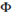 a convex function. This system was considered in 2 where the author showed the existence of global weak solution for the homogeneous system (1). Another system of the type (1) was considered in 3 as a generalization to the scalar Buckley-Leverett equations describing two phase flow in porous media. The system (1), recently, has been object of constant studies, in 4 the author considered the particular case in which
a convex function. This system was considered in 2 where the author showed the existence of global weak solution for the homogeneous system (1). Another system of the type (1) was considered in 3 as a generalization to the scalar Buckley-Leverett equations describing two phase flow in porous media. The system (1), recently, has been object of constant studies, in 4 the author considered the particular case in which 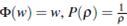 , in this case the two characteristics of the system (1) are linear degenerate, solving the Riemann problem the existence and uniqueness of delta shock solution were established. In this line in (5) the authors considered the case
, in this case the two characteristics of the system (1) are linear degenerate, solving the Riemann problem the existence and uniqueness of delta shock solution were established. In this line in (5) the authors considered the case 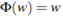 and
and 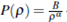 with
with 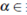 (0,1), the existence and uniqueness of solutions to the Riemann problem was got by solving the Generalize Rankine-Hugoniot condition. In both cases, when
(0,1), the existence and uniqueness of solutions to the Riemann problem was got by solving the Generalize Rankine-Hugoniot condition. In both cases, when 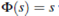 the system (1) models vehicular traffic flow in a highway without entry neither exit of cars, in this case the source term represents the entry or exit of cars see 6),(7),(8 and reference therein for more detailed description of source term.
the system (1) models vehicular traffic flow in a highway without entry neither exit of cars, in this case the source term represents the entry or exit of cars see 6),(7),(8 and reference therein for more detailed description of source term.
Notice that when w is constant, the system (1) reduces to the scalar balance laws
and from the second equation in (1), g should be of the form
g = wf.
Moreover, if we make h(p) = 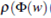 - P(p)) the global weak solution of the Cauchy problem
- P(p)) the global weak solution of the Cauchy problem
there exists if h(p) is a convex function and the source term is dissipative i.e.,
For details on the above result see [9], [10] and references therein. In this work we assume the following conditions,
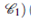 f, g are Lipschitz functions such that
f, g are Lipschitz functions such that
wf (P, w)= g(p, w), f (0,0)= 0.
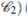 There exist a constant M > 0 such that
There exist a constant M > 0 such that
for [S]> M.
P(0) = 0, lim pP'(p) = 0, lim P(p) = ∞,
Remark 1.1. By example if f (p, w) = p, then g(p, w) = pw. In this case we have the non-symmetric system with lineal damping.
Making m = pw, system (1) can be transformed in a symmetric system
For this system, making F (p, m) = 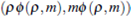 , we obtain
, we obtain
so the eigenvalues and eigenvector of dF are given by
From (2) and (3), the k-Riemann invariants are given by
Moreover,
By 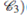 condition, the system (6) is linear degenerate in the first characteristic field, non linear degenerate in the second characteristic field and non strictly hyperbolic. In this paper we obtain the main following theorem
condition, the system (6) is linear degenerate in the first characteristic field, non linear degenerate in the second characteristic field and non strictly hyperbolic. In this paper we obtain the main following theorem
Theorem 1.2. If the initial data
with .The total variation of the Riemann invariants W0(x) be bounded, and the conditions
.The total variation of the Riemann invariants W0(x) be bounded, and the conditions 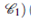
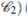
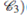 holds, then the Cauchy problem (1), (5) has a global bounded weak entropy solution and wx(x, t) is bounded in L1
holds, then the Cauchy problem (1), (5) has a global bounded weak entropy solution and wx(x, t) is bounded in L1
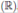 . Moreover for w constant, P is the global weak solution of the scalar balance laws
. Moreover for w constant, P is the global weak solution of the scalar balance laws
Pt + h(P )x = f (P),
2 A priori bounds and existence
In order to get weak solutions, in this section we investigate the problem of the existence of the solutions for the parabolic regularization to the system (1)
with initial data
We consider the transformation m = pw, replacing in (6) we have
with initial data
Proposition 2.1.
Let £ > 0. The Cauchy problem (6)-(7) has a unique solution for any (p0, w0). Moreover, if (p0, w0)
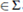 their solutions (p£, m£) satisfies
their solutions (p£, m£) satisfies
The proof of this theorem is postponed at the end of the section. We begin with some lemmas that will be useful afterward.
Let
U = (p,m)T, H(U) = (f (U),g(U))
and M = DF where F(p,m) =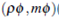 .Then the system (8) can be written in the form
.Then the system (8) can be written in the form
Ut = £Uxx + MUx + H.
For any C1, C2 constants let
G 1 = C 1 - W, (10)
G 2 = Z - C2, (11)
where W, Z are the Riemann invariants given in (4). We proof that the region
is an invariant region.
with K constant, then p(x, t) 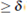 (£, T) > 0 in (0, T).
(£, T) > 0 in (0, T).
For the proof of this lemma see [11, Lemma 2.2].
Lemma 2.3. The functions G1 and G2 defined in (10) and (11), are quasi-convex .
Proof. Let r = (X,
Y) be a vector. If 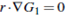 then
then 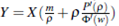 thus
thus
Lemma 2.4. If the condition 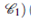 holds, then G
1
, G
2
satisfy
holds, then G
1
, G
2
satisfy
Proof. From (10) and (11), we have that 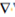 G1 =
G1 = 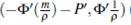 and
and 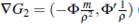 then
then
From the Theorem 14.7 in [12], the region 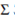 defined in (12) is an invariant region for the system (8). It follows from (10), (11) that
defined in (12) is an invariant region for the system (8). It follows from (10), (11) that
Therefore,
we appropriately choose C 1 , C 2 such that
By (13) we have the proof of Proposition 2.1.
3 Weak convergence
In this section we show that the sequence (p £, m £) has a subsequence that converges the weak solutions to the system (8). For this we consider the following entropy-entropy flux pairs construct in 2 by the author
The Hessian matrix of n is given by
then we have that
where X = (
px, mx
). If 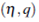 is an entropy-entropy flux pair, multiplying in (8) by
is an entropy-entropy flux pair, multiplying in (8) by 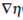 (p, m) we have
(p, m) we have
Replacing the equation (14) in (15) we have
Chose a function 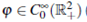 satisfying
satisfying 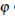 = 1 on [-
L, L
] x [0, T]. Multiplying (16) by
= 1 on [-
L, L
] x [0, T]. Multiplying (16) by 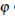 and integrate the result in
and integrate the result in 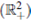 we have
we have
From the Proposition 2.1 we have
As a consequence of the inequality (17) we have the following lemma.
Lemma 3.1. For any £ > 0, if(p, m) is a solutions to the Cauchy problem (8), (9), then 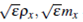 are bounded in
are bounded in 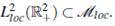 .
.
We denote by 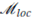 the space of Radon Measures. For any bounded set
the space of Radon Measures. For any bounded set 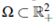 we have
we have
when £ -> 0.
Thereby,
Lemma 3.2.
Proof. The proof of (21) is a consequence of the Lemma 3.1 and the inequalities (18), (19) and the Murat's Lemma. Multiplying in (20) by g' we have
By a similar argument in the inequality (18) we have
From the Lemma 3.1 the last term in (22) is in. 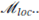 By the Murat's Lemma we conclude the proof of (20).
By the Murat's Lemma we conclude the proof of (20).
Now we can stablish the proof of the main theorem. According to the Young's measures, there exists a probability measure vxt associated with the bounded sequence ( p£, w£ ) such that for almost (x, t), vxt satisfies the following Tartar equation,
for any entropy-entropy flux pair, where 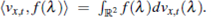 We consider the following entropy-entropy flux pairs
We consider the following entropy-entropy flux pairs
Notice that  = 0, then we have that
= 0, then we have that
where 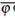 denotes the weak-star limit w * - lim
denotes the weak-star limit w * - lim 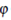 (
u£
). Therefore
(
u£
). Therefore
Using the strong convergence of p£ and Ф ( w£ ) we have
The relation (23) includes the pointwise convergence of w£ if p > 0.
4 Conclusion
This paper deals with a 2 x 2 inhomogeneous system of conservation laws of non-symmetric type, we extended the results of Lu 2 under adecuate conditions on the source term.