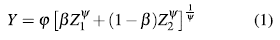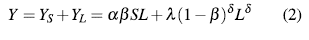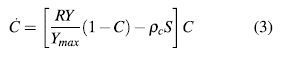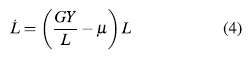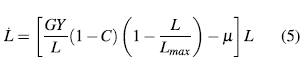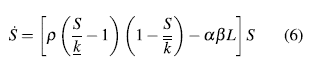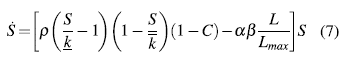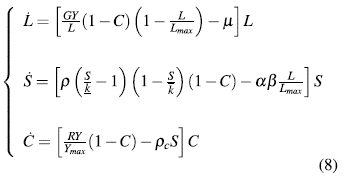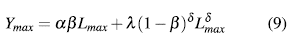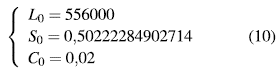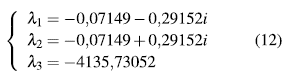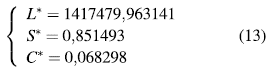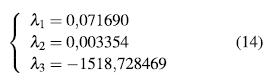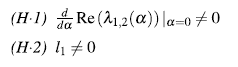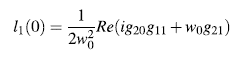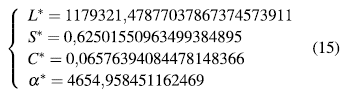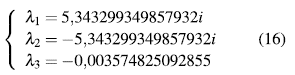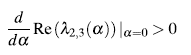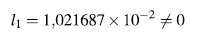Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. INTRODUCCIÓN
La idea general de lo que es desarrollo sostenible se encuentra consignada en el informe de Brundtland de 1987 [1], en el cual se plantea la posibilidad de obtener un crecimiento económico basado en políticas de sostenibilidad y expansión de la base de recursos ambientales y como propósito tiene analizar, criticar y replantear las políticas de desarrollo económico globalizador. En 1992 se publica lo que se conoce como Agenda XXI, suscrita por 172 países miembros de Naciones Unidas donde se comprometen a aplicar políticas ambientales, económicas y sociales en el ámbito local encaminadas a lograr un desarrollo sostenible, además se establece que cada región o cada localidad, por su parte desarrollará su propia Agenda Local XXI, en la que deberían participar tanto ciudadanos, como empresas y organizaciones sociales, con el objetivo de generar y consensuar un programa de políticas sostenibles.
El artículo se compone básicamente en la formulación del modelo y en la aplicación de técnicas del análisis no lineal como instrumento para medir la sostenibilidad.
2. MODELO
Se presentará un sistema de ecuaciones diferenciales ordinarias de primer orden autónomo que permita estudiar la interacción dinámica entre los recursos renovables, la fuerza laboral y la tasa de contaminación.
2.1 Función de producción
Se entiende por función de producción la relación que existe entre el producto obtenido y la combinación de factores que se utilizan en su obtención. En este artículo adoptamos una función de producción CES que generalmente se expresa como sigue:
La ecuación (1) representa la producción obtenida por dos formas diferentes de producir Zi, que por lo general se expresan en términos del acervo de capital K, recursos renovables S y la fuerza laboral L. Φ se interpreta como el factor tecnológico, P como el factor de preferencia y ψ como un coeficiente de elasticidad, ver [2,3].
Siguiendo con la misma metodología que en [2], tomamos por simplicidad ψ = 1y adoptamos que
donde Y s (primer término) es la producción obtenida por la explotación de recursos renovables y Y l (segundo término) la producción generada por las demás actividades económicas. En este caso el parámetro a hace referencia al factor tecnológico utilizado para explotar los recursos renovables S, 1 es un factor de proporcionalidad que indica que el resto de las actividades económicas dependen exclusivamente del crecimiento de la fuerza laboral L y del coeficiente de elasticidad δ .
2.2 Contaminación
Suponemos que la contaminación ambiental de una región se puede medir con una tasa 0 ≤ C ≤ 1. Existen actividades económicas que generan contaminación, pero el medio ambiente es capaz de regenerarse. No obstante existen actividades económicas que causan un daño irreversible al medio ambiente o en la cual la tasa de regeneración es muy lenta. Además, si se tienen buenos recursos renovables estos contribuyen a que el medio ambiente se regenere. Lo antes dicho se puede representar mediante la siguiente ecuación dinámica:
donde Ymax es la producción máxima que se puede alcanzar, R representa un factor que incrementa la contaminación ocasionada por la producción y Pc la tasa de regeneración del medio ambiente generada por el cuidado de los recursos renovables. La expresión (1 - C) es un factor de control que permite que C ≤ 1.
2.3 Demografía de la región
En [2] se propone la ecuación (4) para estudiar la dinámica poblacional y básicamente expresa que el crecimiento de la fuerza laboral L depende del crecimiento de la producción Y y se ve afectada por una tasa de mortalidad o migracional µ.
donde G es un tasa que representa el crecimiento de la fuerza laboral L a medida que la producción lo hace. Ahora, el crecimiento poblacional se ve afectado por la contaminación ambiental y por la fuerza laboral máxima L max que puede soportar la región. Por lo tanto, la ecuación (4) puede ser complementada como:
2.4 Ecuación dinámica de los recursos renovables
Tomando como referencia el modelo formulado en [2] en la cual se plantea una ecuación dinámica para los recursos renovables:
donde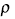 
es un parámetro de renovación de los recursos renovables, 
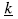es la capacidad mínima de recursos naturales necesaria para que exista regeneración y 
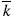es la capacidad de carga máxima de recursos renovables que puede soportar la región.
La tasa de crecimiento de los recursos renovables también se ve afectada por la contaminación ambiental, por lo tanto, para acoplar la ecuación dinámica (6) con la contaminación proponemos la ecuación (7).
3. SISTEMA ACOPLADO
De lo anterior se tiene un sistema conformado por tres ecuaciones diferenciales ordinarias de primer orden, que permiten estudiar la interacción dinámica entre la fuerza laboral, los recursos renovables y la tasa de contaminación:
Por simplicidad del modelo y de las simulaciones suponemos que la variable de estado S ε [0,1] y en virtud de la ecuación (2) se puede estimar el valor de la producción máxima como una función de las variables de estado dada por la ecuación (9).
El sistema de la ecuación (8) es un sistema autónomo de la forma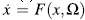 
, donde 
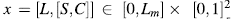es el vector de variables de estado y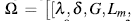 
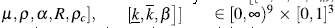es el vector de parámetros del sistema, con 
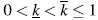. Claramente 
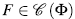donde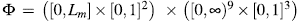 
. Lo anterior garantiza la existencia y unicidad de soluciones ver [4].
Suponemos que los recursos renovables S se miden como una tasa disponible y que también la tasa de contaminación se miden como tasas entre [0, 1].
4. MEDICIÓN DEL DESARROLLO SOSTENIBLE EN EL SISTEMA
Para que el sistema conformado por (8) alcance el desarrollo sostenible "desarrollo que satisface las necesidades de la generación presente, sin comprometer la capacidad de las generaciones futuras de satisfacer sus propias necesidades" [1], podemos pensar en el comportamiento del sistema en estado estacionario. Es decir, cuando dada una condición inicial el sistema alcanza un punto de equilibrio estable donde los recursos S, la tasa de contaminación C, la población L y los parámetros íí estén dentro de unos rangos permitidos. Claramente de esta parte se encargarán las entidades gubernamentales.
Para encontrar un punto de equilibrio estable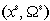 
es necesario resolver el sistema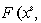 
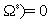y para i = 1, 2, 3 se debe tener que Re(λi) < 0, donde λ
i
son los valores propios de la matriz jacobiana evaluada en el punto de equilibrio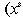 
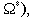, [5]. Estos puntos pueden ser encontrados empleando el método de Newton Raphson (ver [6]).
Las cuencas de atracción del punto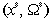 
juegan un papel importante, pues es el conjunto de condiciones iniciales que converge al punto de equilibrio [5]. En el caso en que el punto sea estable y esté en un rango aceptable que permita medir sostenibilidad tanto para los valores de los parámetros como de las variables de estado, entonces la cuenca de atracción del punto de equilibrio permite obtener un conjunto de condiciones iniciales que garantice también sostenibilidad.
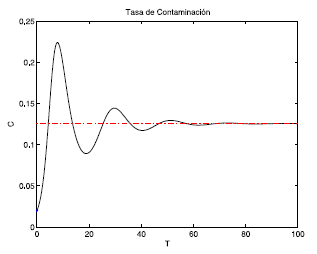
A manera de ejemplo, damos una configuración de los parámetros dados en la Tabla 1 y bajo la condición inicial dada en la ecuación (10) integramos el sistema empleando el software Matlab con un integrador ode23tb en un intervalo de tiempo [0,100], donde se alcanza un punto de equilibrio dado por la ecuación (11).
Utilizando la ecuación (9) obtenemos el valor de Y max = 30525198371,16166.
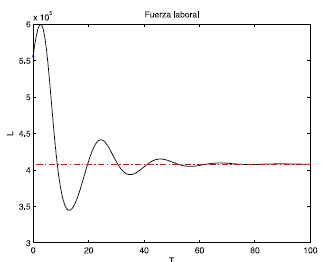
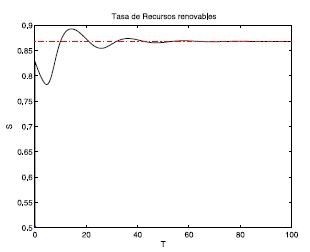
Cabe anotar que la fuerza laboral L se puede normalizar con el valor L m para trabajar con una tasa entre [0, 1] y así interpretar los resultados como un porcentaje de la fuerza laboral. En las Figuras 1, 2 y 3, el punto azul representa la condición inicial, la línea punteada roja el punto de equilibrio.
Los valores propios correspondientes al punto de equilibrio dado en la ecuación (11) estan dados en la ecuación (12), donde se puede apreciar que la parte real de todos los valores propios es negativa, garantizando así que es un punto de equilibrio estable.
Otra forma en la que se puede alcanzar un desarrollo sostenible empleando técnicas del análisis no lineal, encontrando órbitas periódicas en el estado estacionario. Para ello, es necesario identificar condiciones sobre los parámetros para tener una bifurcación de Hopf.
Consideremos los parámetros dados en la Tabla 2, para estos valores obtenemos un punto de equilibrio como se muestra en la ecuación (13), el cual es un punto de equilibrio inestable ya que existen valores propios con parte real positiva como se ve en la ecuación (14). Esto significa que cualquier condición inicial lo suficientemente cercana al punto de equilibrio hace que la trayectoria se aleje de él.
La configuración dada en la Tabla 2 permite obtener un punto de equilibrio en el cual la tasa de contaminación es menor respecto a la configuración de la Tabla 1. Lo cual desde el punto de vista de la definición de desarrollo sostenible es bueno.
4. 1 Continuación Numérica de Equilibrios
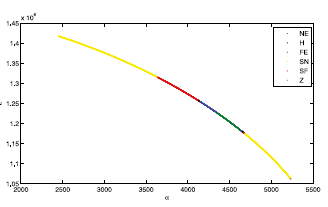
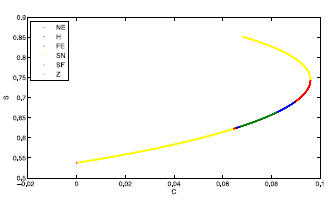
Consideramos los mismos valores de los parámetros de la Tabla 2 a excepción del parámetro a que se varía para estudiar el comportamiento del punto de equilibrio dado en la ecuación (13) bajo la variación de a. La curva de continuación de equilibrios (método implementado de [7,8]) que se muestra en las Figuras 4 y 5, muestran dos posibles puntos de Hopf que analizaremos con más detenimiento en la siguiente sección.
Emplearemos las convenciones de [9] que permitirán interpretar el comportamiento de los puntos de equilibrio dentro de la curva de continuación.
Para puntos de equilibrio hiperbólicos (valores propios con parte real no nula) empleamos la siguiente notación:
NE: Todos los valores propios son reales negativos.
FE: Dos valores propios complejos conjugados con parte real negativa y el otro valor propio es real negativo.
SN: Tres valores propios reales donde alguno
SF: Dos valores propios complejos conjugados con parte real positiva y el otro valor propio es real.
Y para puntos de equilibrio no hiperbólicos utilizamos:
4.2 Bifurcación de Hopf
Definición 1. ( [10] , p. 80) La bifurcación correspondiente a la presencia de λ1,2 = ±iw 0 ,w 0 > 0, es llamada una bifurcación de Hopf (o Andronov-Hopf).
Definición 2. (Bifurcación de Hopf, [10] , p. 67) Las condiciones que especifican sistemas genéricos que demuestran esta bifurcación son los siguientes:
La primera condición (transversalidad) significa que un par de valores propios complejos conjugados λ1,2(a) cruzan el eje imaginario con una velocidad distinta de cero. La segunda condición (no degeneramiento) implica que una cierta combinación de coeficientes de Taylor incluyendo los coeficientes de tercer orden no se desvanecen. Una fórmula explícita para l1(0) se consigue en ( [10] , p. 99) :
4.3 Prueba Numérica de la existencia de la bifurcación de Hopf
De la curva de continuación numérica (Figuras 4 y 5) se pueden apreciar dos posibles puntos de Hopf, pero solo realizaremos la prueba numérica para el punto de bifurcación H dado en la ecuación (15).
4.3.1 Valores propios imaginarios puros
La matriz jacobiana evaluada en el punto de equilibrio de la ecuación (15) tiene como valores propios los de la ecuación (16).
4.3.2 Condición de transversalidad (H-1)
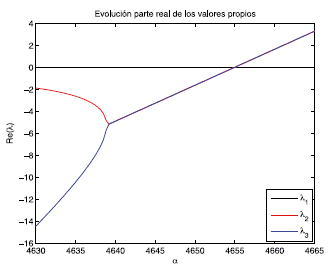
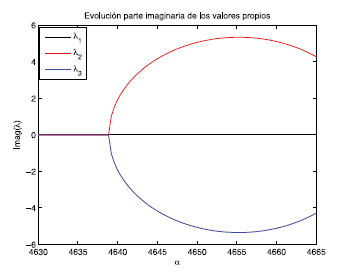
En la Figura 6 se muestra que para el valor del parámetro a* dado en la ecuación (16), la parte real del valor propio complejo es igual a cero y además por ser esta función creciente en una vecindad de a* se cumple (H-1).
En la Figura 7 se observa que la parte imaginaria del valor propio λ2 alcanza un máximo local en el punto de bifurcación, análogamente la parte imaginaria del valor propio λ3 en el punto de equilibrio.
4.3.3 Condición de no degeneramiento (H-2)
Empleando la Definición 2 se calculó el primer coeficiente de Lyapunov dado en la ecuación (17)
En [10] se caracterizan las bifurcaciones de Hopf y por ser el primer coeficiente de Lyapunov se concluye que es una bifurcación de Hopf subcrítica, lo que indica que se tiene un ciclo límite inestable. En términos de sostenibilidad, los ciclos límites inestables también pueden indicar en cierta forma sostenibilidad, pues para que una trayectoría se escape del ciclo límite necesitaría mucho tiempo de evolución y más aún cuando el coeficiente de Lyapunov es pequeño, otra forma de medir sostenibilidad en este caso sería implementar control sobre los parámetros para que el punto de equilibrio inestable dentro del ciclo sea estable. En el caso en que el ciclo límite sea estable no hay mucho por hacer, ya que las trayectorias por dentro del ciclo límite y por fuera de él convergen al ciclo marcando claramente sostenibilidad (Caso del otro punto de Hopf).
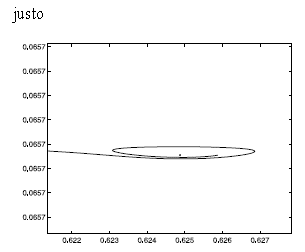
En la Figura 4 se puede observar un pequeño segmento de curva azul antes del punto de Hopf y otro segmento de color rojo después del mismo punto, ver ecuación 15. Tomando un punto de equilibrio representativo sobre el segmento azul, el punto H (punto negro) y otro punto sobre el segmento rojo, se muestran en las Figuras 8, 9 y 10 los diagramas de fase, tomando condiciones iniciales (Puntos verdes) cercanas a cada punto respectivamente. Se puede observar que en el segmento azul, la trayectoria que parte del punto verde converge hacia el punto azul, garantizando la estabilidad del punto de equilibrio antes de la bifurcación de Hopf. Luego en la Figura 9 se puede ver que la trayectoria que inicia desde el punto verde presenta occilaciones cercanas al punto de equilibrio H (punto negro). Finalmente, en la Figura 10, la trayectoria que parte del punto verde se aleja del punto de equilibrio rojo, garantizando así la inestabilidad del punto de equilibrio.
Las simulaciones presentadas en las Figuras 8, 9 y 10 fueron realizadas con el software Matlab empleando como integrador el ode23tb con tolerancias relativas y absolutas de 1 x 10-6.
5. CONCLUSIONES
Se presenta un modelo conformado por un sistema autónomo de ecuaciones diferenciales de primer orden complementando el modelo formulado por D'alessandro, en el cual se acopla con una ecuación dinámica de contaminación ambiental, que permite estudiar la interacción dinámica entre la fuerza laboral, los recursos renovables y la contaminación ambiental para una región. Sin embargo es díficil poder estimar los parámetros a una región específica debido a la falta de series estadísticas de contaminación ambiental y del uso de recursos renovales.
Las técnicas del análisis no lineal y bifurcacional son de gran ayuda para determinar comportamientos no lineales del sistema, estos comportamientos pueden ser empleados para la toma de decisiones en los modelos de desarrollo sostenible. La bifurcación de Hopf super crítica genera un ciclo límite estable que puede ser interpretado como un esquema sostenible dentro de la definición del informe de Bruntlandt, la bifurcación de Hopf subcrítica nos muestra hasta qué valor se puede variar un parámetro en una curva de continuación de equilibrios para que el punto de equilibrio cambie su estabilidad de estable a inestable, lo cual es importante debido a que un punto de equilibrio estable dentro de unos parámetros permitidos puede determinar un esquema sostenible, esto se logra con las cuencas de atracción del punto de equilibrio, ya que se garantiza por su estabilidad.
