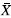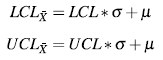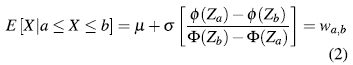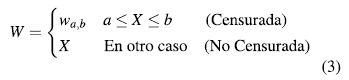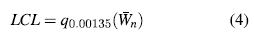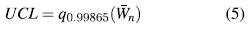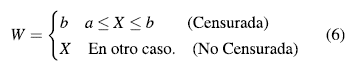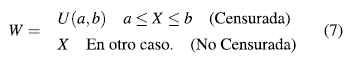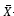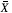Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. INTRODUCCIÓN
En ciertos casos el monitoreo de procesos trabaja con datos censurados, situación en la cual no se conoce el valor exacto de una característica de calidad monitoreada, básicamente debido a que durante el estudio, por posibles limitaciones de tiempo, costos, o en la precisión del instrumento de medición, no se logra conocer el valor exacto de la característica de calidad y la única información que se obtiene es que esta se encuentra dentro de algún intervalo. En la literatura del control estadístico de procesos se ha abordado la censura por diferentes autores. Por ejemplo [1] estudian el caso de censura a derecha durante el monitoreo de procesos, centrándose en censura a derecha tipo I, con una proporción de censura mayor al 50 %, y proponen una carta de control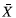 
basada en el valor esperado condicional (CEV), considerando una distribución normal para la variable de interés bajo control. Así mismo [2] proponen una carta 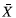CEV con censura a derecha considerando una distribución Weibull para los datos. [3] plantean el caso de censura tipo II y construyen una carta con el fin de monitorear el parámetro de forma en la distribución Weibull. [4] desarollan una carta CUSUM basada en la razón de verosimilitud para el monitoreo de los parámetros de escala y de forma de la distribución Log-logística con censura a derecha. [5] exponen el uso del CEV convergente para imputar la censura, centrándose en caso de censura a derecha con distribución Weibull. [6] contruyen una carta para monitorear la media del proceso considerando censura a derecha y una distribución Rayleigh. Los trabajos antes mencionados, en relación al monitoreo de media del proceso, mejoran el rendimiento de la carta tipo Shewhart tradicional con censura alta (mayor al 90 %), bajo la distribución dada, pues estas cartas mostraron ser más potentes en la detección de desviaciones de la media del proceso que la tradicional.
[1] exponen una situación en la cual son usadas barras mecanizadas como galgas, con un diámetro determinado por los límites de especificaciones de producto, para controlar el diámetro de ciertas arandelas involucradas en la producción de toma - corrientes. Si la barra con mayor diámetro entra en el orificio de las arandelas, entonces se ha excedido el límite de especificación superior, y si la barra más pequeña no entra en el orificio, el diámetro de esta es menor que la especificación inferior. Para las unidades que no están dentro de especificaciones se les mide el diámetro, en tanto, que las unidades dentro de especificaciones quedan censuradas en el intervalo definido por los límites de especificación. Este tipo de censura es conocida como censura tipo I a intervalo. El interés del presente artículo es proponer una metodología para la construcción de una carta de control tipo Shewhart que permita monitorear la media del proceso cuando se tiene censura tipo I a intervalo y la variable a monitorear es 
; también se estudia la potencia de las cartas propuestas en la detección de desviaciones en la media de X, en la fase II de control, en comparación con la carta tipo Shewhart tradicional, con el fin de determinar si las mejoras halladas por otros autores en el tema de la censura en control estadístico de procesos con datos censurados, se mantienen para el caso de censura a intervalo. Cabe notar que bajo el esquema de monitoreo planteado, las unidades buenas son las que quedan censuradas y por tanto se espera una alta censura en estado estable, pues de lo contrario el proceso no estaría en control y no sería un proceso capaz ni se podría seguir el esquema de monitoreo descrito. También se pretende determinar, cuál mecanismo de imputación puede ser más apropiado, entre aquel basado en el valor esperado condicional (CEV), usando el límite superior del intervalo de censura, o bien, usando un valor aleatorio de una uniforme en el intervalo [a, b] de especificación.
En la sección 2 se presentarán las tres cartas propuestas que permiten abordar la problemática de la censura. En la sección 3 se estudia la potencia de cada una en la detección de cambios en la media del proceso en comparación con la carta tipo Shewhart. Finalmente se presenta un caso simulado donde se puede evidenciar la eficacia de las cartas y finalmente concluir sobre la mejor metodología a seguir.
2. CARTAS X EN DATOS CON CENSURA A INTERVALO
En esta sección se procede a desarrollar tres cartas de control 
para tratar la falta de información resultante por la censura a intervalo, la cual se presenta cuando una observación sobre un característica de calidad X , queda dentro del intervalo de censura [a, b], siendo a y b los límites de especificación para esta característica y por tanto, no es observada su medida exacta, solo se sabe que está dentro de dicho intervalo. La idea de las cartas consiste en reemplazar cada observación censurada por un valor cercano al verdadero que tomaría la variable si hubiese sido observada. Para ello, se estudian tres mecanismos de imputación, a saber: la imputación mediante el valor esperado condicional (CEV), imputando la observación censurada con el límite superior del intervalo de censura y por último se usará el método mencionado por [7] donde se propone reemplazar la observación censurada con el valor de una uniforme dentro del intervalo de censura.
La finalidad de las cartas de control propuestas es monitorear y detectar cambios en la media del proceso cuando se presenta censura tipo I a intervalo en las observaciones, las cuales tendrán tanto límite inferior como límite superior de control. Para hallar los límites de control en las tres cartas se considera un proceso bajo control y que la variable aleatoria X, que representa la característica de calidad a monitorear, tiene una distribución N(µ ,o2). En todos los casos, los límites serán inicialmente calculados de forma estándar considerando que X ~ N(0,1) con una cantidad de subgrupos m = 10000, tamaños de subgrupo n = 3,5,10,20 y diferentes proporciones de censura p entre 0 y 1. Los límites de control requeridos en las cartas propuestas para una distribución N(µ,o2) pueden ser obtenidos como [1]:
Donde u y o son los parámetros del proceso bajo control y el UCL y LCL son los límites superior e inferior de control estándar obtenidos mediante simulación bajo una jV(0,1). Los límites estándar dependerán de la carta implementada.
2.1 Carta de Control CEV-X con censura a Intervalo
Considerando el procedimiento desarrollado por [1] se procede a implementar una carta similar para el caso de censura a intervalo. La idea es reemplazar cada valor censurado en la muestra por el valor esperado condicional (CEV), para ello se define un intervalo de censura [a, b] y de acuerdo a esto obtiene el CEV como:
Donde Z α = (α - µ)/σ y Zb = (b - µ)/o . Luego,
se define la variable W como:
Los límites de control para la carta son probabilísticos y calculados mediante simulación, considerando una probabilidad de falsa alarma de 0.0027. El límite superior es hallado como el cuantil 0.99865 y el inferior como el cuantil 0.00135 de la distribución de las medias muestrales (
), para un n dado, basado en 10000 simulaciones. De modo que:
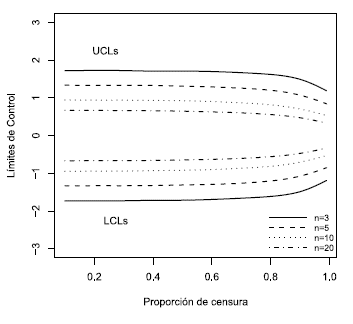
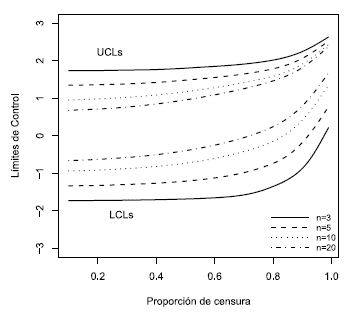
Dichos límites dependen de la proporción de censura p y del tamaño de subgrupo racional n usado en el monitoreo del proceso. Los límites de control estándar para la carta CEV-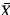
se presentan en el Figura 1 luego de aplicar un suavizamiento spline, en la cual se logra observar que dichos límites son simétricos y se vuelven más estrechos a medida que el tamaño de subgrupo n aumenta.
2.2 Carta de control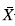 
- b con censura a Intervalo
El procedimiento para construir la carta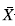 
- b es similar a la carta CEV 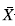, solo cambia el método de imputación, donde cada dato censurado será reemplazado por el límite superior de censura, construyendo así la variable W (ver ecuación 6). Este método de imputación ha sido más popular en confiabilidad y análisis de supervivencia, donde los datos son tratados como si fueran censurados a derecha debido a la disponibilidad de métodos para la inferencia con este tipo de censura. Es posible imputar con el punto medio del intervalo de censura, pero como se estudia en [8] dicho método puede llevar a estimaciones más sesgadas al implementar métodos no paramétricos y al trabajar bajo una distribución diferente a la normal. Los límites estándar para la carta 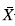- b también son probabilísticos y son obtenidos de manera similar como se expone en las ecuaciones (4) y (5) para los 
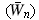en este caso. Dichos límites se pueden ver en la figura 2 luego de aplicar un suavizamiento spline, bajo los mismos niveles de censura y tamaños de subgrupo. En la Figura 2 se aprecia que los límites dejan de ser simétricos cuando la proporción de censura es mayor a 0.2
2.3 Carta de control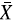 
-U con censura a Intervalo
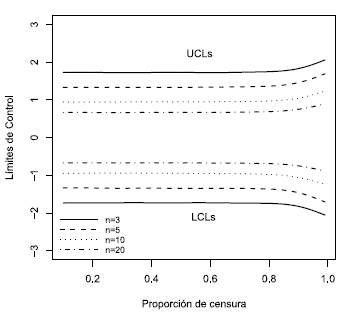
La metodología de la carta 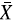-U consiste en imputar cada observación censurada por un valor aleatorio de una uniforme dentro del intervalo de censura [a, b], construyendo la variable W (ecuación 7). En este caso, los límites estándar para la carta también son obtenidos mediante las ecuaciones (4) y (5) para la variable resultante al aplicar el método de imputación de esta carta, los cuales son también probabilísticos. En la Figura 3 se tienen los límites de control estándar obtenidos por simulación para la carta 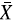-U, luego de aplicar un suavizamiento spline. En dicha figura se logra observar que estos son simétricos y constantes hasta una proporción de censura aproximada de 0.8, después de la cual se vuelven más amplios para todos los tamaños de muestra considerados.
Recapitulando, la construcción de las cartas propuestas para censura tipo I a intervalo implican los siguientes pasos, asumiendo µ y σ conocidos:
Hallar el UCL y LCL mediante las Figuras 1, 2 ó 3 dependiendo de la carta a construir, del tamaño del subgrupo n y proporción de censura p.
Sea Xj j la i-ésima observación en el j-ésimo subgrupo racional con i = 1, 2, n y j = 1,- 2, m. Para cada Xj j censurada en el intervalo [a, b] se toma como observación el valor de wj j según el método de imputación definido por la carta (ver ecuaciones 3, 6 y 7).
Finalmente, calcularlo
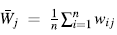(promedio de subgrupos) y graficar contra límites calculados. Si hay puntos por fuera de límites se estudian las causas asignables que lo generen, permitiendo así mejorar la calidad del proceso.
2.4 Potencia comparativa de las cartas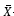 
propuestas y la carta tipo Shewhart
En la práctica, la carta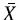 
tipo Shewhart es la más usada para monitorear la media del proceso, por tanto, resulta de interés comparar la potencia de esta con las tres cartas propuestas ante censura a intervalo. Para poder realizar la comparación todas las cartas deben tener la misma probabilidad de falsa alarma cuando el proceso esté en control, la cual se fija en 0.0027. La carta 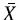tradicional con límites 
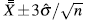ignora la censura y la asimetría presente en las observaciones censuradas, registrando el valor del punto medio del intervalo de especificación como si fuese el valor observado para las unidades que quedan censuradas. Luego, si se usan los límites 3o la probabilidad de falsa alarma será diferente a la deseada. Para construir la carta tipo Shewhart tradicional los límites son calculados como 
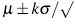donde el valor de k se busca tal que garantice la probabilidad de falsa alarma deseada. La potencia de cada carta es hallada como la probabilidad de detectar cambios en la media del proceso dado que efectivamente se presentó una variación, es decir, se calcula 
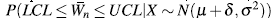con δ el cambio en la media, donde W
n
son las medias por subgrupo de tamaño n de la variable W obtenidas luego de implementar uno de los mecanismos de imputación.
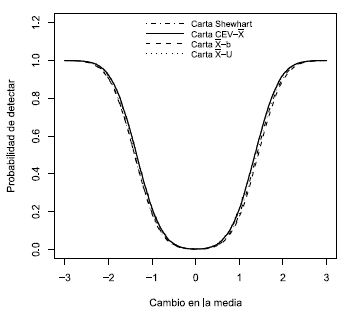
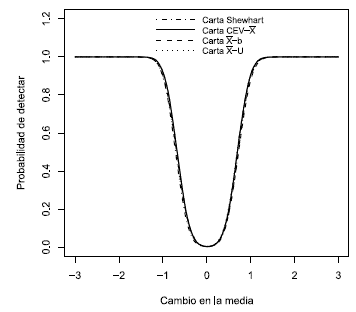
En la Figura 4 se puede observar que para una proporción de censura del 50 % todas las cartas tienen una potencia muy similar para un tamaño de muestra pequeño n = 5; algo similar sucede en la figura 5 para un tamaño de muestra mayor, n = 20, donde la potencia es prácticamente igual; por lo que cualquiera de estas cartas podría ser implementada.
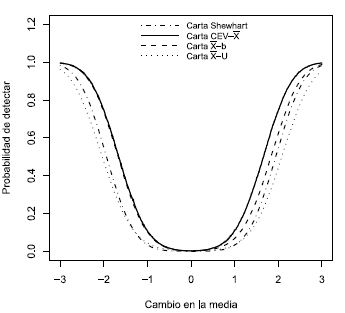
Cuando se tiene una proporción de censura del 95%, la Figura 6 muestra que en la detección de decrecimientos en la media, las cartas CEV -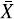
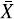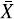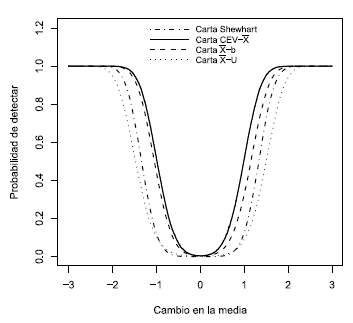
y - b son las más potentes, con igual probabilidad de detectar. Mientras que en la detección de incrementos en la media, la carta CEV - es aquella con mayor potencia, incluso respecto a la carta 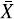- b para un tamaño de muestra n = 5. En la Figura 7 se observa que la carta CEV - 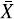es la más potente en la detección tanto de crecimientos como decrecimientos en la media, seguida por la carta 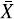- b, la cual muestra ser menos sensible en la detección de crecimientos y un poco menos potente en la detección de decrecimientos; esto debido que al imputar con el límite superior del intervalo de censura, los límites de la carta estarán orientados a monitorear valores cercanos a dicho límite por ende más fácilmente detectarán decrecimientos que crecimientos. Las Figuras 6 y 7 muestran que la potencia de la carta Shewhart es menor respecto a las cartas CEV - 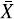y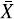 - b, por tanto ambas cartas propuestas mejoran el rendimiento de la Shewhart cuando se presenta censura a intervalo para ambos tamaños de muestra; también se obtiene que la potencia de la carta 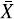- U es la más baja respecto a todas las demás con alta censura, incluso respecto a la tradicional, siendo la menos recomendable en este caso.
3. CASO SIMULADO
Con el fin de observar el desempeño de las cartas propuestas, se procede a calcular los límites de control para cada una de éstas considerando distribución normal con media µ = 10, desviación estándar σ = 2.5, e intervalo de censura o límites de especificación [5.1,14.9]. En este caso se considera que los parámetros son conocidos ya que se está en fase II de monitoreo. Los límites con parámetros conocidos para las tres cartas, están determinados en la Ec. (1), donde LCL y UCL son los límites estándar dados en las Figuras 1, 2 y 3 para la proporción de censura p = 0.95 y n = 5. Por tanto,
Se simularon 40 subgrupos de tamaño n = 5 provenientes de una distribución normal con media µ = 10, desviación estándar σ = 2.5 y una proporción de censura p = 0.95, de los cuales, los primeros m 1 = 30 subgrupos fueron generados en control. Cada observación dentro de límite de especificación es imputada por un valor determinado dependiendo de la carta usada. Los m 2 = 10 subgrupos restantes fueron simulados con corrimiento gradual en la media de 0.5o cada dos subgrupos, generando que los últimos dos presenten un corrimiento de 2.5 o. Para la construcción de las cartas se toma en consideración los 40.
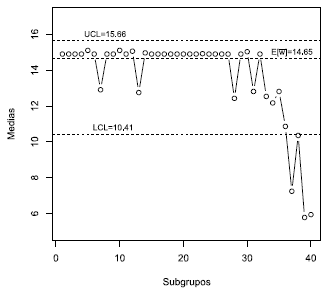
En las figuras 8, 9, 10 y 11 se pueden observar las cartas de control propuestas y la carta Shewhart tradicional para los subgrupos simulados. En dichas figuras se puede ver que para "grandes" corrimientos en la media todas las cartas logran detectar; pero son las cartas CEV-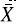
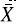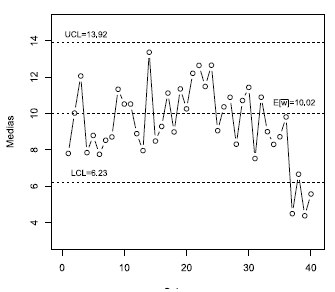
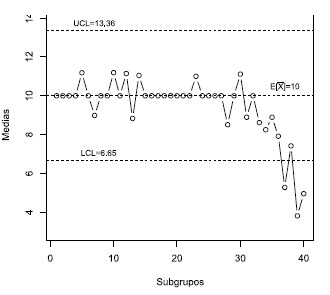
y - b las que detectan más rápido que el proceso está fuera de control, ya que como se muestra en las figuras 8 y 9, detectan punto por fuera de límites a partir del subgrupo 37, con un decrecimiento de 2o en la media, e incluso para el subgrupo 36, con un corrimiento de 1.5o ya se está bastante cerca del límite inferior para estas dos cartas, lo cual no se observó en la carta 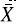-U (figura 10) ni en la carta tradicional_(figura 11). Adicionalmente, en las cartas CEV- 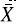y 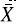-b hay un cambio en el patrón de comportamiento con tendencia de decrecimiento sistemático, cosa que no se evidencia en las otras dos cartas. Por tanto, las cartas 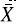-U y la tradicional no reflejan eficazmente que el proceso se ha salido de control.
4. CONCLUSIONES
Cuando se desea monitorear la media de un proceso productivo y se tiene un conjunto de observaciones registradas bajo censura a intervalo tipo I con una alta_proporción de censura, la carta de control CEV-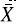, considerando normalidad en los datos, puede ser aplicada, pues demuestra ser más potente para detectar cambios en la media del proceso que la carta tipo Shewhart tradicional, tanto en los casos con prorción de censura del 50 y del 95% y tamaños de muestra pequeños y grandes. Con alta proporción de censura (95%), la carta CEV- 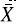es un poco más sensible a decrecimientos en la media que la carta 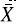-b y aún más sensible cuando hay incrementos. La carta 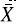- U es más insensible a movimientos en la media, pues imputa con un valor al azar. Estas diferencias con alta censura son el escenario a destacar, pues es lo esperado para un esquema de monitoreo donde las unidades aceptadas son las censuradas. Cabe resaltar que a medida que la proporción de censura aumenta todas las cartas van perdiendo potencia, pero es la carta CEV- 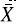quien logra mejores resultados. Las cartas de control propuestas no solo permiten ver si el proceso está en control, si no que adicionalmente ayudan a determinar si hay corrimientos en la media que puedan generar una señal futura, por lo cual se prefieren en lugar de las cartas por atributos que monitorean solo si la variable está o no está dentro de un intervalo de especificación.
Adicionalmente, se tiene que las cartas propuestas son para fase II de control, donde se asumen parámetros conocidos, y si estos no se conocen deben ser estimados basados en una muestra inicial, en la cual es necesario obtener observaciones exactas para poder tener información con la cual estimar con cierto nivel de precisión y estudiar el efecto de la estimación de parámetros en el desempeño de las cartas propuestas.
