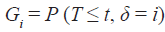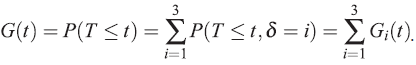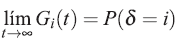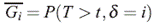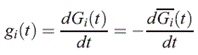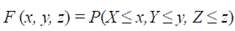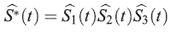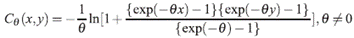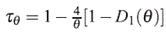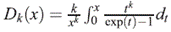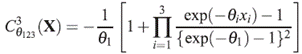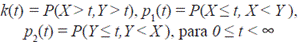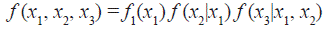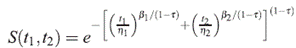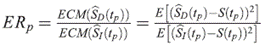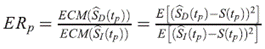1. INTRODUCCIÓN
Un sistema con tres modos de falla puede ser modelado usando un modelo de riesgos competitivos, el sistema fallará cuando se presente cualquiera de los tres modos de falla, es decir, el tiempo de falla observado del sistema es el mínimo de los posibles tiempos de falla de los respectivos modos de falla, además un modo de falla censura a los otros dos modos. La metodología tradicional asume independencia entre los tiempos de falla para la estimación de la función de supervivencia marginal, pero comúnmente este supuesto no se cumple. Para riesgos competitivos la estructura de los datos obtenidos no permite estimar la función de supervivencia ni las densidades marginales, esto es el llamado problema de identificabilidad. En el caso de dos riesgos competitivos, el estimador cópula gráfico permite estimar la función de supervivencia marginal bajo una cópula conocida y la dependencia entre los dos riesgos que compiten. Cuando se tienen modelos de riesgos competitivos con más de dos riesgos, se considera el método denominado combinación de riesgos, propuesto por [1], el cual es una extensión del estimador cópula gráfico, propuesto por [2], y es usado para la estimación de la función de supervivencia. En este trabajo se analiza la función de supervivencia para un modelo con tres riesgos bajo distintas dependencias entre los modos de falla que compiten, por medio del método antes mencionado. Para encontrar la estimación de la función de sobrevivencia se supone independencia entre los modos de falla. En teoría de probabilidad las funciones llamadas cópulas son en realidad funciones de distribución que representan las relaciones de dependencia entre las variables aleatorias. Las funciones cópula bidimensionales son funciones bivariadas que unen o bien copulan dos funciones de distribución univariadas para construir funciones de distribución bivariadas. La cópula representa una forma paramétrica conveniente para modelar la estructura de dependencia en distribuciones conjuntas de variables aleatorias. Este concepto de cópula permite construir modelos que van más allá de los estándares en el análisis de dependencia entre variables estocásticas. La metodología de cópula es capaz de capturar relaciones no lineales y en particular permite relacionar eventos extremos que ocurren en la naturaleza [3].
En el caso no paramétrico la función de sobreviviencia conjunta, en un problema con múltiples modos de falla, no puede ser completamente identificada en la situación usual cuando sólo se conocen los tiempos mínimos de falla [4]. Incluso en el caso paramétrico los datos pueden contener poca información sobre el coeficiente de asociación entre las variables y resulta necesario hacer algunos supuestos al respecto [5]. Para el caso no paramétrico el estimador cópula gráfico de [2], resuelve el problema bajo el supuesto del conocimiento de la forma funcional de la cópula que proporciona la estructura de asociación entre los riesgos competitivos. Es de anotar quebajo independencia el problema de identificabilidad no existe. Para la estimación de la función de supervivencia; [1] proponen el método denominado combinación de riesgos para un modelo con más de dos riesgos competitivos cuando la cópula es Arquimediana. En éste método la variable combinada es sólo creada conceptualmente para verificar lo relacionado con la identificación. [6] realizaron estudio de dependencia entre los riesgos, el cual es un procedimiento para una iteración serial de cópulas Arquimedianas las cuales tienen la misma estructura de dependencia, además estas cópulas que utilizaron para ese estudio satisfacen las propiedades de simetría y asociatividad, las cuales son requeridas para que el método de combinación de riesgos funcione en forma adecuada. [1] realizaron una aplicación del método de combinación de riesgos en un estudio de desempleo en Alemania, donde consideraron tres riesgos competitivos con igual dependencia, en este trabajo se estudia el caso en el cual los tres riesgos que compiten presentan diferentes dependencias. [7] estudiaron una extensión del estimador cópula gráfico para un modelo con más de dos riesgos competitivos e ilustraron la metodología con datos de la confiabilidad de interruptores tipo FL245 en Interconexión Eléctrica S.A. E.S.P. (ISA) y mostraron la utilidad de la temática en confiabilidad industrial.
En este trabajo, se estudian distintas dependencias entre los riesgos, se usa la técnica de los C-D Vines cópulas, los cuales trabajan con una variedad de cópulas bivariadas, dichas cópulas se pueden seleccionar de manera independiente y permiten tener una amplia gama de posibilidades para la caracterización de la dependencia de los riesgos que compiten. Se estudiaron tres casos de dependencia. En el primer caso dos de los tres riesgos tienen igual dependencia y el riesgo restante es independiente a los anteriores. En el segundo caso se tomaron dos riesgos con igual dependencia y el otro riesgo con una dependencia alta. En el tercer caso se tomaron los tres riesgos con distintas dependencias.
2. RIESGOS COMPETITIVOS
El tiempo de falla de un sistema con múltiples modos de falla puede ser modelado como un sistema en serie o un modelo de riesgos competitivos. El tiempo de falla observado es el mínimo de esos tiempos potenciales individuales, donde cada unidad tiene un tiempo potencial de falla [8].
Los datos para un modelo de riesgos competitivos trivariado se presentan como una variable aleatoria bivariada de la forma (T δ), con Tel tiempo mínimo de falla T = mín(X ,Y, Z), con tiempos de falla pontenciales X, Y, Z y donde δ es una variable discreta, la cual toma valores de 0 si la observación es una censura, 1 cuando la falla se presenta por el primer modo de falla, 2 cuando la falla se presenta por el segundo modo de falla y 3 cuando la falla se presenta por el tercer modo de falla.
3. CONCEPTOS FUNDAMENTALES
[8] presenta algunos conceptos fundamentales para el desarrollo del presente trabajo.
La función de subdistribución o función de incidencia acumulada (FIA) para el modo de falla i, i = 1, 2, 3, viene dada por:
La función de distribución total es la probabilidad que un evento de cualquier tipo ocurra en o antes del tiempo t, es decir, es la suma de las FIA para todos los tipos de eventos;
En ausencia de riesgos competitivos la función de distribución total se encuentra en el intervalo [0, 1]. Luego en presencia de riesgos competitivos la función de subdistribución sólo puede tomar valores hasta P(δ = i) puesto que:
Por lo tanto, la función G i (t) no es una función de distribución propia.
La función de subsobrevivencia es la probabilidad de que el modo de falla i no ocurra antes del tiempo t
La función de subdensidad para el modo de falla i y T continuo, se define de la siguiente manera
4. PROBLEMA DE IDENTIFICABILIDAD
Para el caso no paramétrico, la distribución conjunta en un problema con múltiples modos de falla no puede ser completamente identificada, en la situación usual, cuando sólo se conocen los tiempos mínimos de falla, para un problema de este tipo la aproximación usada para especificar el modelo de riesgos competitivos es vía tiempos latentes. Para el caso trivariado se tienen tiempos de falla potenciales X, Y, y Z asociados a cada modo de falla, donde si el sistema falla a causa del primer modo de falla, el segundo y el tercero no pueden ser observados. Así T = mín(X ,Y, Z) determina el tiempo de falla del sistema completo.
Dada la tripleta (X,Y, Z) con distribución multivariada:
y funciones de distribución marginales para cada modo de falla, los cuales tienen la siguiente forma F 1(t) = P(X ≤ t), F2(t) = P(Y ≤ t) y F3(t) = P(Z ≤ z). Uno de los intereses en riesgos competitivos es identificar las distribuciones marginales de las variables a partir de los datos de riesgos competitivos. En el caso donde los tiempos de falla son independientes, las distribuciones marginales son identificables, y corresponden a las funciones de distribución. Si este supuesto no se tiene, entonces a partir únicamente de los datos, en riesgos competitivos, no es posible identificar las distribuciones marginales y la distribución conjunta de los tiempos, existen muchas funciones de distribución conjunta diferentes que comparten las mismas funciones de subdistribución, lo cual es llamado el problema de identificabilidad [4].
Para este problema en particular existen varias soluciones:
1. Asumir independencia.
2. Asumir una estructura de dependencia conocida usando una cópula particular para la distribución conjunta de los modos de falla, [2] proponen el algoritmo cópula gráfico.
3. Especificar un modelo paramétrico.
5. ESTIMACIÓN DE LA FUNCIÓN DE SOBREVIVENCIA BAJO INDEPENDENCIA
Según [9] para un sistema en serie con tres componentes independientes, la función de distribución para el tiempo mínimo T está dada por:
F(t) = 1 - [1 - F 1(t)][1 - F 2(t)][1 - F3(t)]
donde (X, Y, Z) son los tiempos de vida asociados a cada una de las tres componentes, T = mín(X, Y, Z) es el tiempo observado y F i , i = 1, 2, 3, las respectivas funciones de distribución para los componentes. La función de sobrevivencia S(t) = 1 - F (t), para el caso de modos de falla independientes es:
S(t) = S 1 (t)S 2 (t)S 3 (t).
donde S i (t), i = 1, 2, 3 son las funciones de sobrevivencia de las tres componentes. Para un sistema con tres componentes en serie y tiempos de falla dependientes, F(t) tiene la siguiente forma:
F(t) = 1 - P(X > t,Y > t, Z > t)
Para este caso, la evaluación se debe hacer con respecto a la distribución conjunta de X, Y y Z, en la cual se debe incluir el parámetro de dependencia. La función de sobrevivencia para este caso es:
S(t) = P(X> t,Y> t, Z> t).
El estimador de la sobrevivencia del tiempo mínimo de falla de un sistema con tres modos de falla independientes que compiten S(t), se
denotará 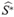 (t), Para obtener este estimador basta multiplicar las funciones de sobrevivencia estimadas bajo una distribución específica, donde para cada función marginal se estiman los parámetros, considerando los tiempos del otro modo de falla como tiempos de censura o censurados.
(t), Para obtener este estimador basta multiplicar las funciones de sobrevivencia estimadas bajo una distribución específica, donde para cada función marginal se estiman los parámetros, considerando los tiempos del otro modo de falla como tiempos de censura o censurados.
donde 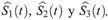 corresponden a las funciones de sobrevivencia marginales estimadas para cada modo de falla.
corresponden a las funciones de sobrevivencia marginales estimadas para cada modo de falla.
6. CÓPULAS
Una cópula se define como una distribución multivariada, con distribuciones marginales uniformes en [0, 1]. Las cópulas permiten representar de manera separada la estructura de dependencia y las distribuciones marginales de una distribución multivariada. La metodología de cópulas se ha convertido en una herramienta importante a la hora de modelar o generar datos multivariados.
[3] contiene una gran cantidad de información acerca del modelado de dependencias con cópulas. Combinando varias distribuciones marginales con diferentes cópulas, es posible modelar distribuciones multivariadas con una amplia gama de marginales y tipos de dependencia. A continuación se muestra el teorema fundamental para cópulas conocido como el Teorema de Sklar.
Teorema 1 (Teorema de Sklar). Sean Y 1 , ... ,Y p variables aleatorias con función de distribución conjunta F, con marginales F 1 , ... , F p respectivamente. Entonces existe una cópula C tal que satisface:
F (y 1 ,... , y p ) = C(F 1 (y 1 ), ... , F p (y p ))
Si F 1 , ... , F p son continuas, entonces C es única. Inversamente, si C es una cópula y F 1 , ... , F p y funciones de distribución, entonces F es una función de distribución conjunta con marginales F 1 , ... , F p .
Para nuestro caso hacemos uso del teorema para los casos bivariado y trivariados.
6.1 Cópulas Arquimedianas
Un importante caso particular de cópulas son las cópulas Arquimedianas, se caracterizan por la facilidad con que pueden ser construidas y por la gran variedad de estructuras de dependencia que pueden reproducir. En este trabajo se utilizó la cópula Frank debido a que en la implementación del algoritmo de [1], ellos la utilizaron en un estudio de desempleo en Alemania y los resultados fueron óptimos.
6.2 La cópula Frank
La cópula Frank tiene grandes propiedades, captura el rango completo de dependencias, incluye las cópulas de cota superior de Fréchet cuando θ →−∞de cota inferior de Fréchet cuando θ → ∞ y de independencia cuando θ → 0. La cópula Frank proporciona cantidades cerradas y permite mayor facilidad al momento de programar [10].
6.3 τ de Kendall
El t de Kendall, mide el grado de asociación entre dos variables aleatorias, en particular para las marginales dos a dos de un modelo de riesgos trivariado dependiente generado en nuestro caso. Está dado como sigue:
donde D k (x) es la función Debye, la cual está definida para cualquier entero k por:
El t de Kendall, cumple con la siguientes propiedades lím θ →−∞ t θ = -1, lím θ →−∞ t 6 = 1 y lím6-0 t θ = 0 (independencia).
7. ESTIMADOR CÓPULA GRÁFICO
[2] aplican cópulas Arquimedianas en modelos de riesgos en competencia con datos censurados dependientes, proponiendo un estimador no paramétrico para las distribuciones marginales llamado estimador cópula gráfico, el cual da solución al problema de identificabilidad, dicho problema es resuelto con datos de riesgos competitivos y bajo el supuesto de que la cópula y su paramétro de asociación son conocidos de antemano.
En el marco de riesgos competitivos se observa T j = mín(X j ,Y j ) y δ j = I (Xj≤Yj) (j = 1, ... , n). Suponiendo que P (X j = Y j ) = 0. Haciendo uso de esta información se puede estimar directamente:
donde p 1(t) y p 2(t) corresponden a las funciones de subdistribución.
[2] afirman que bajo el supuesto de independencia entre X y Y, las distribuciones marginales son determinadas de manera única por esas probabilidades, muestran en general, que si la cópula de (X,Y) es conocida, entonces las distribuciones marginales son determinadas de manera única por los datos de riesgos competitivos.
El estimador cópula gráfico está basado en el algoritmo de búsqueda de raíces, el cual trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que contiene la raíz de la función de variable real. Este método es sencillo y fácil para resolver ecuaciones, se basa en el teorema del valor intermedio, el cual establece que toda función continua f en el intervalo [α, b] y f (α) y f (b) tienen signos opuestos, entonces f tiene al menos una raíz en el intervalo (α, b).
7.1 Extensión del Estimador Cópula Gráfico: Método de Combinación de Riesgos
[1] presentaron una extensión del estimador cópula gráfico propuesto por [2], la propuesta es llamada el método de combinación de riesgos, la cual se aplica a modelos con más de dos riesgos competitivos cuando la cópula es Arquimediana.
A continuación se presentan detalles del método cuando se tienen tres riesgos en competencia.
Sean (T 1, T 2 ,T 3 ) ∈ R 3 + tiempos de falla latentes, de un modelo de riesgos competitivos tridimensional. En éste caso se tienen tres tiempos potenciales X, Y y Z, asociados a tres modos de falla, de manera que cuando la falla se presenta por el primer modo, los otros dos modos de falla no pueden ser observados.
7.2 La dependencia modelada con C-Vine y D-Vine cópulas
[11] proponen los C-Vines y D-Vines para simular distribuciones multivariadas flexibles las cuales son necesarias en distintas áreas. La distribución Gaussiana es muy restrictiva y no puede detectar características como asimetría y colas pesadas, las cuales en los análisis financieros son muy comunes. El uso de las cópulas es un reto en dimensiones superiores donde las cópulas multivariadas estándar tienen o poseen estructuras inflexibles. Los vines cópulas superan estas limitaciones y son capaces de modelar patrones de dependencia complejos al tener una gran variedad de cópulas bivariadas como componentes básicos. Los vines son modelos gráficos flexibles para describir cópulas multivariadas usando una cascada de cópulas multivariadas llamadas pair-copulas. Tales construcciones, descomponen una densidad de probabilidad multivariada en cópulas bivariadas, donde cada pair-copula puede ser elegido de manera independiente de los otros. Esto permite una enorme flexibilidad en el modelamiento de la dependencia. En particular, las asimetrías y la dependencia de las colas pueden ser tenidas en cuenta, así como la independencia condicional para construir modelos más parsimoniosos. Los vines combinan las ventajas de modelización con cópulas multivariadas, es decir, separan del modelo marginal, la dependencia y la flexibilidad de la cópula bivariada.
El número de cópulas disponibles para modelar la estructura de dependencia entre más de dos variables es limitado. De hecho, la gran mayoría de las cópulas paramétricas disponibles son bivariadas. Además, el enfoque basado en una cópula multivariada puede no resultar apropiado cuando los pares de variables presentan estructuras de dependencia diferentes. Finalmente, en muchos casos en que sí se cuenta con una extensión multivariada de la cópula, se utiliza un solo parámetro para describir la estructura de dependencia entre todos los pares de variables, lo cual es una limitación importante si las relaciones entre pares de variables son diferentes. Las construcciones con cópulas bivariadas y los vines constituyen una alternativa al enfoque basado en cópulas multivariadas. Estos modelos permiten extender las cópulas bivariadas a dimensiones superiores utilizando solamente cópulas bivariadas y densidades univariadas como bloques constructivos. El creciente interés en estos modelos se debe a la gran flexibilidad que brindan para modelar una amplia variedad de dependencias combinando cópulas bivariadas de familias diferentes.
7.3 Metodología de los vines
Los vines son una representación gráfica para especificar las llamadas construcciones pair-copulas (PCCs) introducidas por [12]. En particular, las PCC en tres dimensiones, estarían dadas como sigue:
Sea X = (x1, x2, x3)T ~ F con funciones de distribución marginales F1, F2 y F3 y la respectivas funciones de densidad f 1 , f 2 y f 3 , luego la función de densidad trivariada se define como:
Para realizar la selección de la estructura de los C- Vines y D-Vines; se deben seleccionar los pares de variables que serán modeladas explícitamente con cópulas. Un C-Vine resulta apropiado si una variables domina las interacciones entre las variables. Un D-Vine permite una selección más flexible de dependencias.
8. ESTUDIO DE SIMULACIÓN
Se presentan los resultados obtenidos al comparar la función de sobrevivencia verdadera del tiempo mínimo de falla S(t), con la función de sobrevivencia estimada asumiendo independencia entre los modos de falla (SI(t)) y la función de sobrevivencia bajo dependencia (SD(t)) del tiempo mínimo de falla, la cual fue estimada haciendo uso del método de combinación de riesgos, para un modelo de riesgos competitivos trivariado. Se analizan distintas dependencias entre los riesgos, dichas estructuras son generadas mediante la técnica C-DVines.
8.1 Metodología y Escenarios de simulación
En esta sección se describen los escenarios y la metodología de simulación utilizados para el análisis de la función de sobrevivencia en un modelo de riesgos competitivos dependientes trivariados bajo distintas estructuras de dependencia entre los modos de falla.
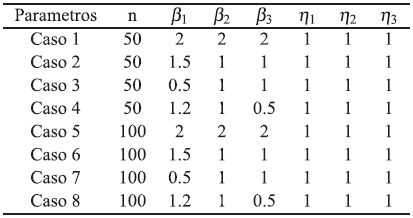
Inicialmente, se generan muestras de tamaño n =50 y n = 100 de tiempos de falla trivariados, con la dependencia deseada entre los riesgos del modelo en riesgos competitivos dependientes y marginales Weibull se tomaron estos tamaños de muestra, puesto que en confiabilidad siempre es de gran interés estudiar problemas con tamaños de muestra pequeños debido a los costos y no es común estudiar problemas con tamaños de muestra demasiado grande.
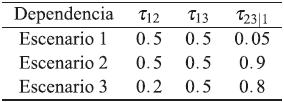
Las dependencias estudiadas entre los modos de falla se relacionan en la siguiente tabla:
Las dependencias propuestas se generaron mediante las técnicas: C-Vines; la cual es apropiada para dependencias donde una de las variables domina toda la estructura de dependencia y D-Vines; permiten una selección más flexible de las dependencias. En el escenario 1 se tomaron dos riesgos con igual dependencia y el otro riesgo independiente a los otros dos. En el escenario 2 se tomaron dos riesgos con igual dependencia y el otro riesgo con una dependencia alta. En el escenario 3 se tomaron los tres riesgos con distintas dependencias.
Seguidamente se encuentra el tiempo mínimo, es decir, T = mín(T 1, T 2, T 3). Se rotulan con 1 si la falla ocurre por el modo de falla 1; 2 si la falla ocurre por el modo 2 y 3 si la falla se presenta por el modo 3.
Para obtener los tiempos de falla Weibull, se hace uso de lo propuesto por [13] en el caso bivariado. Sean T 1 y T 2 tiempos de falla Weibull, una función de sobreviviencia conjunta para la Weibull bivariada se define como sigue:
donde ß 1 , ß 2 son los parámetros de forma y η 1 , η 2 son los parámetros de escala asociados a T 1 y T 2 respectivamente, además 0 ≤ t ≤ 1, es el parámetro de dependencia entre T 1 y T 2 .
En los escenarios Weibull estudiados se consideraron diferentes formas de la función Hazard de los tiempos de falla. Cuando el parámetro ß< 1, la tasa de falla es decreciente, cuando ß> 1, la tasa es creciente y cuando ß= 1, la tasa de falla es constante.
Seguidamente, se estimaron los parámetros para las distribuciones del tiempo de falla para cada riesgo, con estos estimadores se obtienen las funciones de sobrevivencia del tiempo mínimo de falla asumiendo independencia. Luego se estiman las distribuciones marginales para cada modo de falla mediante el método de combinación de riesgos, el cual nos permite estimar la función de sobrevivencia bajo dependencia entre los riesgos del modelo trivariado.
Mediante simulación de Monte Carlo se construyen intervalos de confianza empíricos aproximados al 95 % para los percentiles t p con p=0.05, 0.25, 0.50, 0.75, 0.95, tanto para la función de sobrevivencia estimada bajo independencia y bajo dependencia.
Finalmente, se compararon los dos estimadores en cuestión, calculando la eficiencia relativa ER de (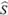 i(t)) con referencia a (
i(t)) con referencia a (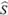 D(t) en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95
D(t) en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95
Si ER p < 1 entonces S I . (t p ) es menos eficiente en relación a S D (t p ) para la estimación de la función de sobrevivencia verdadera en los percentiles estudiados.
9. RESULTADOS
A continuación se muestran los resultados obtenidos en todos los escenarios de simulación analizados:
9.1 Escenario 1 de dependencia
En este escenario se simularon dos riegos con igual dependencia y el otro riesgo se tomó independiente a los anteriores con tamaños de muestrales de 50 y 100. Los riegos tienen dependencia t12 = 0. 5, t13 = 0. 5, t23|1 = 0. 05 y cuyo parámetro de cada cópula son respectivamente; θ 12 = 5.7, θ 13 = 5.7 y 0 = 0.45 y se usó el método de C-Vines, el cual genera la dependencia teniendo en cuenta el primer riesgo.
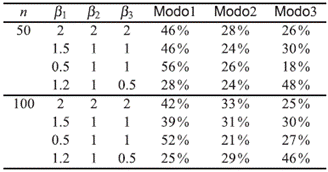
En la Tabla 3, se observa que el porcentaje de falla para cada uno de los modos de falla son mayores o iguales al 15 %, lo que nos garantiza tener buenas estimaciones de la función de sobrevivencia para el tiempo mínimo cuando se realizan las estimaciones bajo dependencia e independencia entre los modos de falla del modelo de riesgos competitivos trivariado dependiente. Los procentajes de falla en la gran mayoría de los casos son distintos, por tanto garantiza que los modelos estudiados no se dejan influenciar por las dependencias. Lo anterior permite ilustrar claramente el problema de identificabilidad y es claro que no se están trabajando con funciones de distribución marginales sino con funciones de sub-distribución [7].
Tabla 3 Porcentaje de falla para el modelo Weibull con tamaños de muestra n = 50, 100 y parámetros de dependencia; t12 = 0. 5, t13 = 0. 5 y t23|1 = 0. 05 y C-Vines.
En la Tablas 4, 5, 6, 7, 8, 9,10, 11 se muestran los límites inferior y superior de la función de sobrevivencia estimada bajo dependencia LI.S D (t) y LS.S D (t) respectivamente. Los límites inferior y superior de la función de sobrevivencia estimada bajo independencia denotados por LI.S I(t), LS.S I (t), y la precisión de cada intervalo de confianza empírico aproximado para la sobrevivencia verdadera en los percentiles r = 0.05, 0.25, 0.50, 0.75, 0.95 y tamaño de muestral 50.
Tabla 4 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo dependencias. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
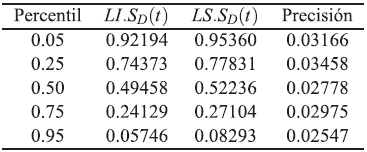
Tabla 5 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo independencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
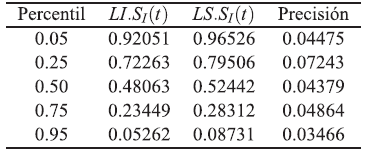
Tabla 6 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo dependencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
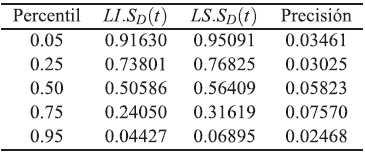
Tabla 7 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo independencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
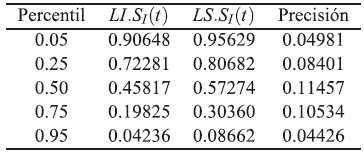
Tabla 8 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo dependencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
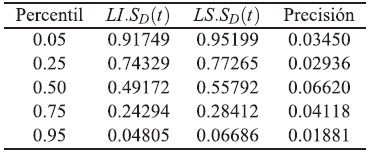
Tabla 9 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo independencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
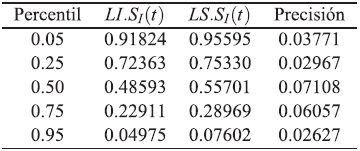
Tabla 10 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo dependencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
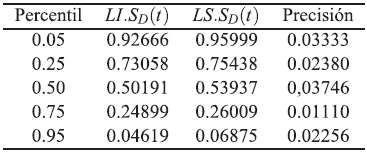
Tabla 11 Intervalos de confianzas empíricos aproximados del 95 % para S(tp) bajo independencia. Modelo Weibull con parámetros ß 1=2, ß 2=2, ß 3=2, η 1 =1, η 2 =1, η 3 =1, n=50 y T 12=0.5, T 13=0.5 y T 23|1=0.05
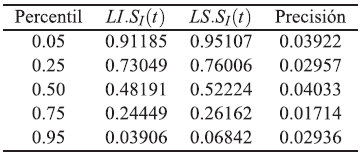
Se evidencia que los intervalos de confianza bajo dependencia en los modos de falla resultan ser más precisos que los intervalos de confianza bajo independencia entre los modos de falla del modelo.
En las tablas se observa que los intervalos de confianza bajo dependencia entre los modos de falla del modelo trivariado siempre se encuentran contenidos en los intervalos de confianza bajo independencia de dicho modelo. En algunos casos el límite inferior o superior se encuentran cercanos al valor verdadero pero lo importante es que contengan al valor de la sobreviviencia verdadera.
Finalmente, se compararon los dos estimadores en cuestión calculando la eficiencia relativa ERp de (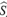 I(t)) con referencia a (
I(t)) con referencia a ( d(t)) en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95
d(t)) en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95
Si ER < 1 entonces S I .(t p ) es menos eficiente en relación a S D (t p ) para la estimación de la función de sobrevivencia verdadera en los percentiles estudiados.
En las Tablas 12, 13 y 14. Se evidencia que el estimador bajo independencia es menos eficiente que el estimador bajo dependencia, puesto que los valores calculados son menores que 1, vale la pena resaltar que en algunos percentiles el valor calculado es cercano a 1 y en general no se evidencia ningún patrón en particular.
Tabla 12 Eficiencia relativa para el escenario 1; modelo Weibull con tamaños muestrales n = 50, 100 y parámetros de dependencia; t 12= 0. 5, t 13= 0.5 y T 23|1=0.05 y C-Vines
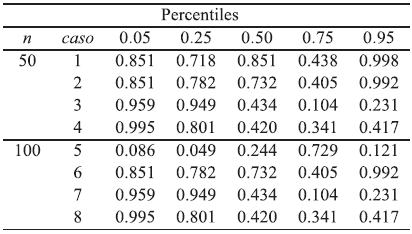
Tabla 13 Eficiencia relativa para el escenario 2; modelo Weibull con tamaños muestrales n = 50, 100 y parámetros de dependencia; t 12= 0.5, t 13= 0.5 y t 23|1= 0.9 y C-Vines
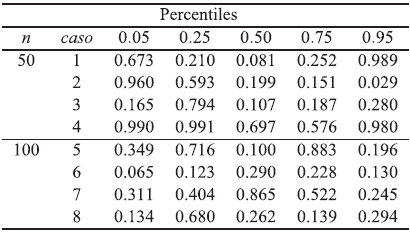
Tabla 14 Eficiencia relativa para el escenario 3; modelo Weibull con tamaños muestrales n = 50, 100 y parámetros de dependencia; t12= 0. 2, t13= 0.5 y t 23|1= 0. 8 y C-Vines
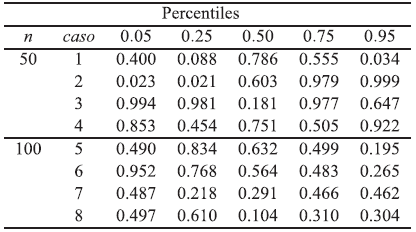
Para efectos prácticos, sólo se muestran los resultados del primer escenario, teniendo en cuenta que se trabajaron los otros dos y dichos resultados fueron similares con respecto a que el estimador bajo dependencia se comporta mejor, que el estimador bajo independencia.
CONCLUSIONES
En gran mayoría de los casos estudiados el estimador bajo dependencia S D (t) presentó mayor eficiencia frente al estimador bajo independencia S . (t) de S(t). Por lo tanto se recomienda utilizar el estimador S D (t) cuando no se tiene certeza de que los tiempos de falla sean independientes.
Los intervalos de confianza para la función de sobrevivencia cuando se asume dependencia entre los modos de falla son más estrechos que los intervalos de confianza para la función de sobrevivencia cuando se asume independencia entre los modos de falla del modelo de riesgos trivariados con marginales Weibull.
Para un modelo de riesgos competitivos trivariados, el método de combinación riesgos (extensión del estimador cópula gráfico) es una buena técnica para estimar las funciones de distribución marginal y la función de sobrevivencia del tiempo mínimo en un modelo en riesgos competitivos, cuando se tiene dos riegos con igual dependencia y el otro independiente a los anteriores, también cuando se tienen dos riesgos con igual dependencia y el otro riesgo presenta una alta dependencia, y por último cuando los riesgos para un caso particular, presentan distintas dependencias (generados por medio de C-DVines).