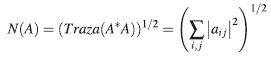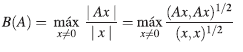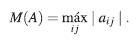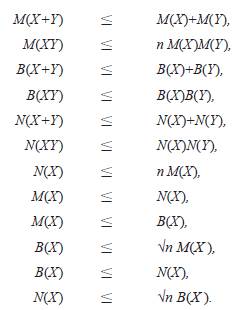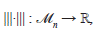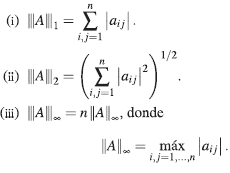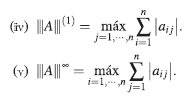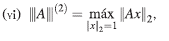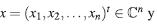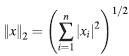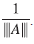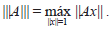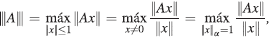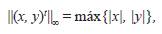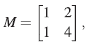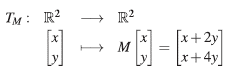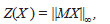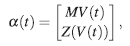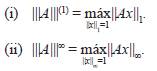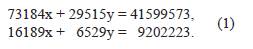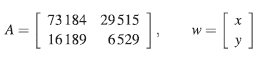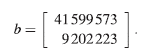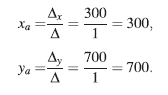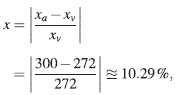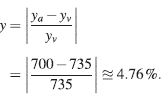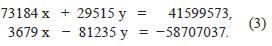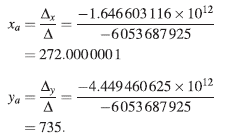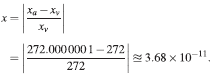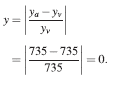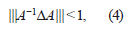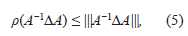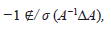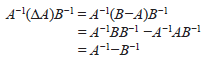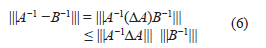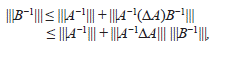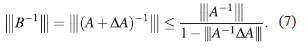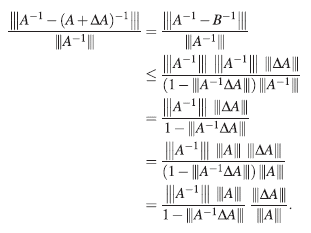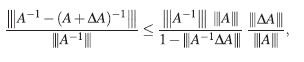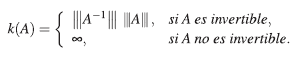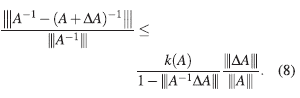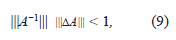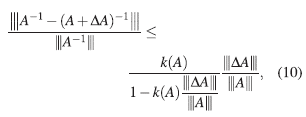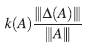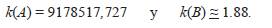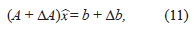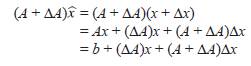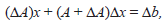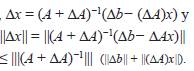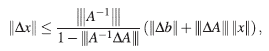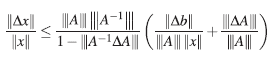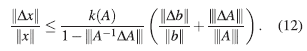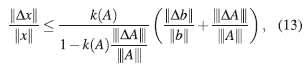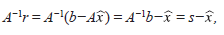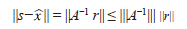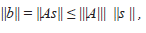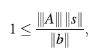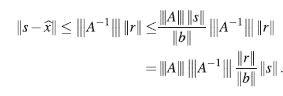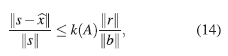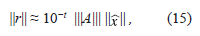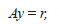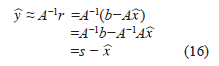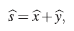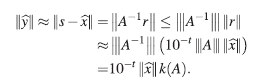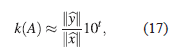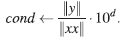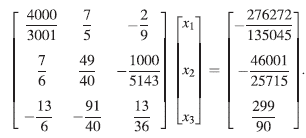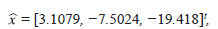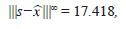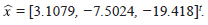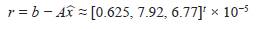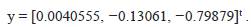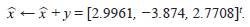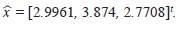1. INTRODUCCIÓN
Un resultado muy conocido del álgebra lineal indica que si A es una matriz cuadrada invertible de orden n con entradas complejas, entonces, el sistema de ecuaciones Ax = b tiene solución única, sin embargo, encontrar dicha solución no siempre es una tarea fácil. La dificultad en el cálculo de una solución para un problema de este tipo se da, o porque la "magnitud" de la matriz o de su inversa podría ser muy grande o porque las entradas de la matriz podrían ser cantidades extremadamente grandes o extremadamente pequeñas, lo que causa que hallar la solución sea una tarea larga, tediosa y poco precisa cuando se trabaja con una aritmética finita, y en algunos casos casi imposible de realizar. Cuando se menciona la "magnitud" de una matriz, se hace referencia al tamaño dado por alguna de las normas matriciales.
Como una posible solución a este inconveniente, se empezó a pensar en el desarrollo de una máquina que hiciera cálculos matemáticos de forma rápida y precisa, uno de los primeros en iniciar la construcción de dicha máquina fue Charles Babbage, (1791-1891) quien es conocido como el "padre de la computación", por el diseño, (no construcción), de lo que podría ser la primera máquina analítica que ejecutó programas de tabulación o computación. Posteriormente, en el marco de la segunda guerra mundial, Alan Turing (1912 - 1954) y John von Neumann (1903 - 1957) contribuyeron en el desarrollo y construcción de las primeras computadoras digitales, como herramientas que facilitaron y agilizaron los cálculos numéricos, como se establece en Turing [10] y en Díaz [5].
Turing es conocido por ser uno de los pioneros de la computación moderna, sus trabajos permitieron la creación de las primeras calculadoras digitales y sus aportes en el proceso para la creación de máquinas que facilitaran los cálculos numéricos fueron significativos. Fue además, uno de los primeros en hablar acerca de lo que ahora se conoce como normas matriciales, sin embargo, él las definió como la "medida de la magnitud de una matriz". Turing en [10] menciona que hay diferentes formas de medir la magnitud de una matriz por medio de un número real, y estas incluyen :
(a) La norma de una matriz A, denotada por N(A) y calculada por:
(b) La expansión máxima, denotada por B(A) y calculada por:
(d) El coeficiente máximo, denotado por M(A) y calculado por:
Turing además estableció las siguientes desigualdades:
Von Neumann y Goldstine, por su parte, presentan en [8] un estudio acerca de la precisión y estabilidad del método de eliminación, como herramienta para hallar la inversa de una matriz de orden n, cuando n es grande. En éste, se presenta el siguiente listado con las posibles fuentes de error:
(a) La formulación matemática que se elige para representar el problema subyacente, ya que ésta puede representarlo sólo con ciertas idealizaciones, simplificaciones y negaciones.
(b) Asumiendo que la formulación matemática no presente errores, la descripción de acuerdo a dicho modelo puede implicar parámetros cuyos valores se deriven directa o indirectamente (es decir, a través de otras teorías o cálculos) de las observaciones. Estos parámetros se verán afectados por errores y estos errores subyacentes causarán errores en el resultado final.
(c) La formulación matemática del modelo puede implicar el uso de funciones trascendentes y operaciones como diferenciación o integración, entre otras, que para ser abordados mediante cálculos numéricos deben reemplazarse por procesos elementales y definiciones explícitas que corresponden a un procedimiento finito y constructivo que se resuelve en una secuencia lineal de pasos. Todos estos reemplazos son aproximados y constituyen por tanto, una tercera fuente de error.
(d) Asumiendo que se puedan superar los tres posibles errores mencionados antes, aún queda una limitación por superar y es el hecho de que ningún dispositivo de cálculo puede realizar todas las operaciones elementales de manera rigurosa y precisa.
Por todo lo antes mencionado, resulta de gran interés estudiar la sensibilidad en la solución de un sistema de ecuaciones lineales cuando se hacen pequeñas perturbaciones en las entradas de los datos. Una herramienta poderosa para controlar dicha sensibilidad es el número de condición de la matriz de coeficientes, éste se puede acotar usando normas matriciales y ha sido objeto de estudio por muchos años. Von Newmann y Turing fueron algunos de los primeros en estudiar los números de condición, ellos centraron sus esfuerzos en buscar cotas superiores para los números de condición. En trabajos más recientes como el presentado por Pyzara et al. en [9], se muestra la relación que tienen los números de condición con la convergencia de algunos métodos iterativos, usados para resolver sistemas de ecuaciones lineales.
Este Artículo está organizado de la siguiente forma: en la Sección 2 se presenta la notación que se utilizará y algunas generalidades concernientes a las normas matriciales. Las propiedades y ejemplos, se enuncian sin sus demostraciones, ya que son resulta- dos ampliamente conocidos en el área del Análisis Matricial, y pueden ser consultados en textos como el de Hõrner [6]. La Sección 3, hace referencia al concepto de condicionamiento de una matriz y se deducen algunas de las cotas que se utilizarán cuando se aborde el problema del refinamiento de soluciones de sistemas lineales. En la sección 4, se presenta la base teórica necesaria para mostrar y desarrollar un método que permite perfeccionar de manera iterativa, los resultados que se obtienen mediante el método de Gauss-Jordan, cuando se trabaja con una aritmética fija con un número prederminado de dígitos. Este tipo de métodos han sido usado recientemente en la solución de sistemas de ecuaciones, tal como se puede observar en los artículos de Arunachalam y Dharmaraja [2], de Calvache et al. [4] y en el de Arun et al. [1], en donde sistemas de ecuaciones integrales, por medio de transformadas de Laplace, se modifican a sistemas lineales de ecuaciones, cuyas primeras soluciones no son tan precisas, pero trabajándolo reiterativamente se encuentran soluciones más precisas, las cuales mediante transformadas inversas de Laplace, conllevan a soluciones aproximadas de los sistemas de ecuaciones integrales. Al algoritmo deducido se le denominará método de Refinamiento. En la Sección 5 se ilustra el método mediante un ejemplo numérico. Por último se enuncian unas conclusiones.
2. NORMAS MATRICIALES
Para empezar se establecen las siguientes notaciones: ℳm,n y ℳn se usan para denotar respectivamente, al conjunto de matrices rectangulares de m filas y n columnas con entradas en ℂ y al conjunto de matrices cuadradas con n filas y n columnas, con entradas en ℂ. Se representa por ℂ n al conjunto de vectores columna, de tamaño n, cuyas entradas son números complejos, es decir ℂ n = ℳn,1. Dada A ∈ ℳm,n, At es la matriz transpuesta de A. La matriz nula se representa por O y en cada caso se asume que tiene el tamaño indicado para que las operaciones a realizar estén bien definidas. La matriz identidad de orden n, se nota por In, y cuando no haya lugar a confusión se representa simplemente por I. σ (A) simboliza el conjunto de todos los valores propios de la matriz A y es llamado el espectro de A, además ρ(A) representa el radio espectral de A, que es el mayor valor absoluto de los elementos de σ (A).
Para el posterior desarrollo del método de Refinamiento, se hace necesario controlarlo de acuerdo con el número de condición de una matriz, y por esta razón se abordará primero el concepto de norma matricial. A continuación se presenta la definición de norma matricial, seguida de algunos ejemplos y propiedades.
Definición 1. Considerando (ℳn,+) como espacio vectorial sobre C, una función,
es una norma matricial sobre M n , si para cada par de matrices A, B є M n y cada λ є C se satisfacen las siguientes propiedades:
||| A||| ≥ 0 y ||| A||| = 0, si y sólo si, A = O .
||| λ A||| = |λ| ||| A|||.
||| A + B||| ≤ ||| A||| + ||| B|||.
||| AB||| ≤ ||| A||| ||| B|||.
Las funciones que satisfacen únicamente las propiedades 1 a 3, son llamadas normas vectoriales y debido a ésto, es válido afirmar que toda norma matricial es una norma vectorial, sin embargo, el recíproco no es cierto.
Ejemplo 2. Dada A є M n , las funciones definidas como siguen, son normas matriciales sobre C.
Nótese que |||.|||∞, es una norma vectorial, pero no es norma matricial.
Propiedad 3. Sean A є M n y |||-||| una norma matricial definida sobre entonces,
(i) |||A2||| ≤ |||A|||2.
(ii) Para cada k ∈ ℤ+, |||Ak||| ≤ |||A|||k.
(iii) Si A es idempotente y no nula, entonces |||A||| ≥ 1.
(iv) |||In||| ≥ 1.
A partir de las normas vectoriales de Cn es posible construir normas sobre Mn .
Teorema 4. Sea || || una norma vectorial en Cn. Se define la función || || de Mn en R, como sigue:
Entonces |||-||| es una norma matricial, llamada norma matricial inducida por la norma vectorial || ||.
Teorema 5. Sean A є Mn, ||-|| una norma vectorial de Cn y ||| ||| su norma matricial inducida, entonces,
(i) |||In||| = 1 .
(ii) Para cada x є ℂn, ||Ax|| ≤ |||A||| ||x||.
en donde, ||·||α es una norma vectorial de ℂn.
En el siguiente ejemplo se presenta una interpretación gráfica de la norma matricial inducida por |·||∞, cuando ésta se trabaja sobre el conjunto de las matrices de orden dos, con entradas reales.
Ejemplo 6. Si en ℝ2 se toma la norma vectorial ||·||∞, definida por
y se considera la matriz,
a ésta le corresponde la transformación lineal,
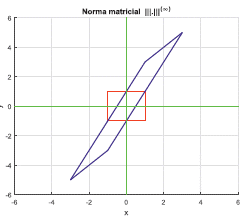
Ahora bien, en la Figura 1, se observan dos gráficas. En color rojo se representan los vectores unitarios con la norma ||·||∞, y en color azul se representan los vectores Z = MX, en donde X es unitario; es decir, la gráfica en color azul representa la imagen bajo M de los vectores de la gráfica en color rojo. Ahora, si para cada vector Z del gráfico en azul, se calcula ||Z||∞ y se toma la máxima de estas normas, es posible ver, que para el ejemplo se tiene que la norma máxima es igual a 6, y se concluye que |||M||| = 6, donde |||·||| es la norma inducida por ||·||∞.
Por otra parte, en la Figura 2 se aprecian tres elementos. El primero está en el plano xy, con color rojo y representa los vectores U de ℝ2, tales que, ||U||∞ = 1; el segundo elemento es la superficie,
siendo X un vector de ℝ2; finalmente con color azul y sobre la superficie se muestra la curva paramétrica
donde V (t) es una parametrización de la curva representada en color rojo. También se aprecia que la mayor altura de la superficie ɀ = Z(X), condicionada a ||X||∞ = 1, es igual a 6; es decir, también se concluye que la norma inducida por ||·||∞, evaluada en M es 6.
A partir del Ejemplo 6 es posible conjeturar la existencia de una relación entre |||·|||∞ y la norma matricial inducida por la norma vectorial ||·||∞. Esto es en efecto cierto y se enuncia formalmente en la siguiente proposición.
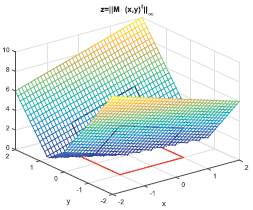
Proposición 7. Dada A ∈ ℳn,
Adicionalmente, se usará el siguiente resultado, el cual es ampliamente conocido:
Proposición 8. Dada A ∈ ℳn,
ρ(A) = ínf {|||A||| | |||·||| es norma matricial en ℳn}.
3. CONDICIONAMIENTO DE MATRICES
En matemáticas se acepta la existencia de números con un número infinito de dígitos, sin embargo, en las computadoras ésto no es posible y por tanto este tipo de números es representado con una aproximación que sólo tiene un número finito de dígitos, es decir, las calculadoras y computadoras usan un subconjunto relativamente pequeño de números racionales para representar a todos los números reales, por esta razón, los números irracionales e infinitos racionales son representados por una aproximación que está lo suficientemente cercana al valor exacto como para que los resultados de muchas operaciones sean aceptables, pero en algunos casos, más comunes de lo que se cree, esto causa diferencias considerablemente grandes entre el resultado obtenido por la máquina y el resultado preciso. El error causado al usar estas aproximaciones para resolver problemas numéricos, fue considerado por Neumann y Goldstine en [8] y ahora es llamado error de redondeo.
Por ejemplo, al solucionar sistemas de ecuaciones lineales, aun cuando éstos tengan pocas variables y pocas ecuaciones, se pueden obtener errores de redondeo, tal como se puede apreciar en el siguiente ejemplo, en el que se presenta un sistema de ecuaciones lineales con dos incógnitas x e y:
Ejemplo 9.
Las soluciones exactas de este sistema son xv = 272 e yv = 735, como puede comprobarse fácilmente al reemplazar estos valores por x e y en (1).
Ahora se resolverá este sistema, usando aritmética de diez dígitos significativos (esta es la aritmética que se utiliza en una gran variedad de calculadoras científicas), trabajando con el método de Cramer.
El sistema (1) se puede escribir matricialmente, como:
donde.
y
Ahora, se calcula:
Por tanto los valores aproximados de x e y, obtenidos por este método son:
Comparando con las respuestas verdaderas, se obtienen los siguientes errores relativos:
Como puede observarse son errores relativos muy grandes.
Ahora se considera el sistema:
Puede comprobarse que las verdaderas respuestas de este sistema son xv = 272 e yv = 735.
Procediendo en forma similar a como se resolvió el sistema (1), se obtiene la solución aproximada:
Comparando con las respuestas verdaderas, se obtienen los siguientes errores relativos:
Estos ejemplos muestran que si
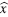 es una solución aproximada del sistema Ax=b, r=b−A
es una solución aproximada del sistema Ax=b, r=b−A
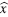 es el vector residual y ||r|| es pequeña, no es necesariamente cierto que el error absoluto, ||x−
es el vector residual y ||r|| es pequeña, no es necesariamente cierto que el error absoluto, ||x−
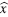 || sea también pequeño. Adicionalmente, es posible asumir que la matriz de coeficientes B, del sistema (3), debe cumplir alguna condición que no cumple la matriz A del sistema (1) y que por esa razón el error de redondeo en las solución del sistema (1) es grande, mientras que el error de redondeo en la solución de (3) es muy pequeño.
|| sea también pequeño. Adicionalmente, es posible asumir que la matriz de coeficientes B, del sistema (3), debe cumplir alguna condición que no cumple la matriz A del sistema (1) y que por esa razón el error de redondeo en las solución del sistema (1) es grande, mientras que el error de redondeo en la solución de (3) es muy pequeño.
Sean ||·|| una norma matricial dada y A ∈ ℳn una matriz invertible, si se quiere calcular la matriz inversa de A, se trabajará con la matriz B = A + ΔA, en donde, ΔA es una perturbación de la matriz A.
y ya que B = A(I + A−1ΔA) y
entonces, (4) y (5) implican que,
y por tanto 0 ∉/ σ (B), es decir, B es invertible.
También se tiene que,
y así,
Además, B−1= A−1−A−1(ΔA)B−1, de donde,
lo que es equivalente a tener,
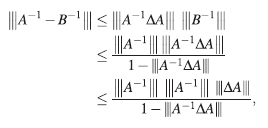
Combinando (6) y (7) se obtiene,
y entonces,
Así, una cota superior para el error relativo en el cálculo de la inversa es:
Con base en esta argumentación, se presenta la siguiente definición.
Definición 10. Sean A una matriz en ℳn y |||∙||| una norma matricial dada, el número de condición de la matriz A con respecto a la norma matricial |||∙|||, se define y denota por:
Hasta el momento se ha encontrado la cota,
Obsérvese que,
Si se fortalece la suposición hecha en (4) y se asume que,
entonces,
es decir, se tiene una cota superior para el error relativo en el cálculo de la inversa de una matriz, en términos del error relativo de los datos y del número de condición, tal cota es llamada, cota a priori.
Si |||A−1||| |||ΔA||| no sólo es menor que 1, sino que es mucho más pequeña que 1, entonces, la expresión del lado derecho en (10), sería muy cercana al valor,
y por tanto es válido pensar que el error relativo en la inversa, tiene el mismo orden que el error relativo en los datos, concluyéndose así que k(A) no es muy grande. Por esta razón, se establece que,
(i) Si k(A) es grande, se dirá que A está mal condicionada.
(ii) Si k(A) es pequeño y cercano a 1, se dirá que A está bien condicionada.
(iii) Si k(A) = 1, se dirá que A está perfectamente bien condicionada.
Todo esto con respecto a una norma matricial específica.
Ejemplo 11. Si nuevamente se toman las matrices A de (1) y B de (3) y la norma matricial |||-||| ∞ , se tiene que,
Es decir, A está mal condicionada, mientras que B está bien condicionada.
4. MÉTODO DE REFINAMIENTO
En este momento se comenzarán a deducir diferentes cotas de error, que permitirán establecer un método iterativo, en el cual en cada repetición se perfecciona cada vez más, la solución inicial dada por el método de Gauss-Jordan. Por supuesto, que este algoritmo que se va a derivar, será útil en caso que la matriz del sistema esté mal condicionada, pues de lo contrario, el método de Gauss-Jordan, dará como solución una muy buena aproximación a la solución exacta del sistema.
Supóngase que se quiere resolver el sistema lineal Ax = b, con A una matriz invertible de ℳ n y b un vector no nulo de ℂ n . Sin embargo por los errores computacionales, en realidad se va a resolver el sistema perturbado
donde A, ΔA ∈ ℳ
n
; b, Δb ∈ ℂ
n
y
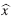 = x + Δx. Para saber qué tan grande podría ser Δx es posible usar algunas normas matriciales para obtener una cota para el error relativo en la solución, en términos del error relativo de los datos y el número de condición de A.
= x + Δx. Para saber qué tan grande podría ser Δx es posible usar algunas normas matriciales para obtener una cota para el error relativo en la solución, en términos del error relativo de los datos y el número de condición de A.
Sea |||·||| una norma matricial de ℳ n , inducida por la norma vectorial ||·||| de ℂn y nuevamente asúmase lo dicho en (4), entonces,
y por (11)
Usando (7), se tiene que,
por lo tanto,
Tomando en consideración la definición de k(A) y ||b|| = ||Ax|| ≤ |||A||| ||x||, se concluye que,
Si nuevamente se asume |||A −1 ||| |||ΔA||| < 1, entonces,
la cual es una cota más débil pero más fácil de calcular. Además, esta cota tiene las mismas características y consecuencias que (10), y si la matriz de coeficientes del sistema de ecuaciones lineales está bien condicionada, entonces, el error relativo en la solución tiene el mismo orden que el error relativo de los datos.
Si se conoce una solución aproximada de Ax = b, ésta puede ser usada para determinar una cota a posteriori. Sean ||∙|| una norma en ℂ
n
, |||∙||| la norma inducida por ||∙||, s la solución exacta de Ax = b y r = b A
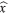 el vector residual. Como
el vector residual. Como
entonces,
y
es decir,
entonces,
Así, el error relativo entre la solución calculada y la solución exacta está acotado como sigue,
en donde la norma matricial usada para calcular el número de condición es la inducida por la norma vectorial ||·||. En un problema bien condicionado el error relativo en la solución es del mismo orden que el tamaño relativo del residuo; en un problema mal condicionado, sin embargo, una solución calculada que produce un residuo pequeño puede todavía estar lejos de la solución exacta.
Por tanto, el número de condición de una matriz dependerá únicamente de las normas de la matriz y de su inversa, pero el cálculo de la inversa está sujeto a errores de redondeo y éstos dependen de la precisión con la que se hacen los cálculos. Si las operaciones se hacen con aritmética de t dígitos de precisión, entonces, la aproximación al número de condición de la matriz A, es el producto de la norma de A con la norma de la aproximación de la inversa de A, obtenido con aritmética de t dígitos. En efecto, este número también depende del método usado para calcular la inversa de A. Por tal razón es conveniente poder estimar el número de condición sin necesidad de calcular directamente la inversa.
Si se asume que la solución aproximada del sistema Ax = b se determina usando aritmética de t dígitos y eliminación gaussiana, en IEEE Computer Society, 2008 [7], demuestran que el vector residual r de la aproximación satisface,
con esta aproximación es posible estimar el número de condición, con aritmética de t dígitos, sin tener que invertir la matriz A.
La aproximación de k(A) con t dígitos significativos viene de considerar el sistema de ecuaciones lineales
este sistema puede ser resuelto usando en el mismo orden las mismas matrices elementales usadas para resolver Ax = b. Si es la solución aproximada de
Ay = r, entonces,
y se obtiene una nueva aproximación de la solución dada por
es decir,
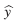 es una estimación del error que se produce cuando
es una estimación del error que se produce cuando
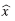 es la aproximación de la solución del sistema original.
es la aproximación de la solución del sistema original.
De las ecuaciones (15) y (16) se obtiene que,
En consecuencia,
es una aproximación para el número de condición asociado al sistema Ax = b, usando eliminación gaussiana y aritmética de t dígitos.
A la repetición sistemática de este proceso se le llama refinamiento iterativo, si el sistema está bien condicionado, una o dos iteraciones serán suficientes para indicar la solución correcta, además existe la posibilidad de una mejora significativa en sistemas mal condicionados, a no ser que la matriz esté tan mal condicionada que k(A) > 10t, como se demuestra en IEEE Computer Society [7].
Además, en [6] se advierte que si A−1 tiene algunas entradas relativamente grandes, entonces, algunas entradas de la solución pueden tener una gran e inevitable sensibilidad respecto a las perturbaciones que se hagan en algunas de las entradas de b y de A.
4.1 Descripción del algoritmo
Todo lo que se acaba de deducir y justificar, se puede sintetizar en el siguiente algoritmo, que sirve para mejorar la aproximación a la solución de un sistema de la forma Ax = b, especialmente cuando la matriz A está mal condicionada. Antes de iniciar la aplicación del algotirtmo se deben elegir, una norma vectorial ||·|| y su norma matricial inducida |||·|||.
Proceso
Se inicializa k ← 0, donde k es una variable que cuenta el número de iteraciones del algoritmo.
Se resuelve el sistema Ax = b, usando el método de Gauss-Jordan, y la respuesta aproximada se guarda en la variable res. Se actualiza k ← k + 1.
Se pregunta si k es menor a n.
i. Se calcula la variable r ← b−A·res.
ii. Se resuelve el sistema Ax = r, usando exactamente los mismos pasos que se realizaron en el ítem 2, y la solución se guarda en la variable y.
iii. Se calcula la variable xx ← res + y.
iv. Se calculan ||y||, ||xx||.
v. Se pregunta si |y | < ET .
Si la respuesta es sí, entonces k ← n e ind ← true. Esta última variable ind indica si ya se obtuvo una solución satisfactoria.
vi. Se actualizan k ← k + 1 y res ← xx.
vii. Se inicia de nuevo el ítem 3.
5. ILUSTRACIÓN NUMÉRICA
Para ilustrar la potencia del algoritmo de Refinamiento Iterativo se va a resolver el siguiente sistema de ecuaciones lineales, el cual está escrito en la forma, Ax = b.
Se puede comprobar que la solución exacta del sistema es s = [3, −4, 2]
t
. Al aplicar el algoritmo de Refinamiento, tomando en consideración un error de tolerancia de 1 × 10
−12
, la norma vectorial ||·||
∞ y su norma matricial inducida |||·|||
∞, se observa que según (17), el número de condición aproximado de la matriz de coeficientes es 1.1427 × 1016, esto significa que la matriz está mal condicionanda, sin embargo, el algoritmo encuentra en doce pasos, una aproximación
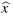 de la solución, para la cual el error absoluto es menor a 1 × 10−12. Algunos de los resultados obtenidos en los doce pasos, son:
de la solución, para la cual el error absoluto es menor a 1 × 10−12. Algunos de los resultados obtenidos en los doce pasos, son:
Primera iteración
Se recuerda que en esta primera iteración, lo que realmente se usa es el método de Gauss- Jordan, con una aritmética de cinco dígitos y se obtiene la aproximación,
obsérvese que el tamaño del error cometido esta dado por
y por ser este resultado tan grande, se aprecia que la respuesta obtenida en este paso, es desastrosa. En las siguientes iteraciones del algoritmo, se pretende disminuir paulatinamente el error de aproximación.
Segunda iteración
1. Se toma la aproximación inicial
2. Se encuentra el vector residual,
3. Se resuelve el sistema Ax = r, tomando exactamente los mismos pasos que se usaron para hallar la primera aproximación,
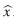 . La solución de este nuevo sistema se guarda en una variable llamada y, en este paso,
. La solución de este nuevo sistema se guarda en una variable llamada y, en este paso,
4. Se calcula ||y||
∞ = 0.79879 y como este valor es mayor al error de tolerancia, se debe realizar una nueva iteración, actualizando el valor de y aplicando nuevamente los pasos 1 a 3. Para actualizar el valor de
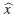 , se suma y al valor de
, se suma y al valor de
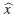 que se obtuvo en el paso anterior. Es decir,
que se obtuvo en el paso anterior. Es decir,
Décimo segunda iteración
Al observar detalladamente los resultados presentados en esta última iteración, es natural preguntar, ¿por qué el proceso no se detuvo en la undécima iteración? El algoritmo no se detiene en una iteración anterior, pues a pesar de que el algoritmo, en algunos casos, imprime el valor
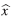 = [ 3, −4, 2]
t
la realidad es que en memoria el valor asignado para
= [ 3, −4, 2]
t
la realidad es que en memoria el valor asignado para
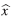 es diferente y por ejemplo en la undécima iteración, el valor ||y||
∞ = 9 .8814 × 10
−8
es mayor al error de tolerancia. Por esa razón es necesario hacer la décimo segunda iteración, en donde sí se puede dar por terminado el algoritmo.
es diferente y por ejemplo en la undécima iteración, el valor ||y||
∞ = 9 .8814 × 10
−8
es mayor al error de tolerancia. Por esa razón es necesario hacer la décimo segunda iteración, en donde sí se puede dar por terminado el algoritmo.
CONCLUSIONES
Para determinar si una matriz, está o no, bien condicionada, se pueden usar las propiedades de las normas matriciales para acotar el número de condición.
Si se usa aritmética finita de t dígitos para hallar la solución de un sistema de ecuaciones lineales mal condicionado, la aproximación inicial va a estar muy lejos del valor exacto, sin embargo, si k(A) < 10t, es posible usar el método de Refinamiento presentado en la Sección 4, para mejorar la aproximación inicial y así, obtener una solución con un error suficientemente pequeño para ser aceptada.