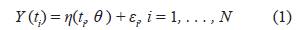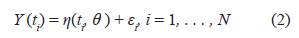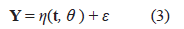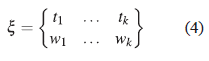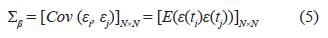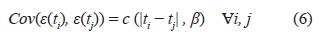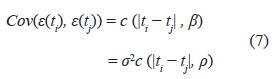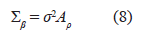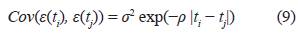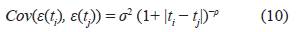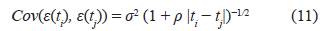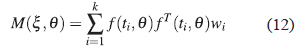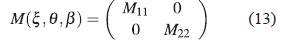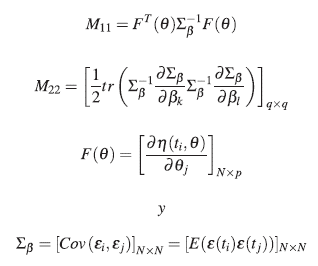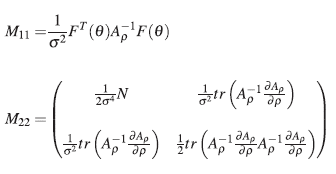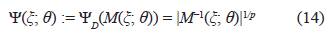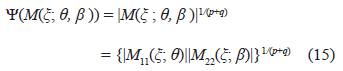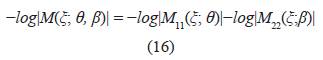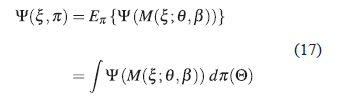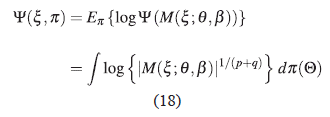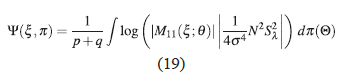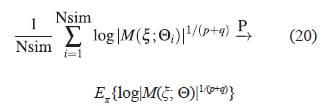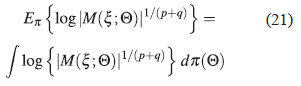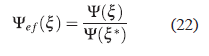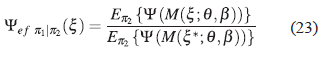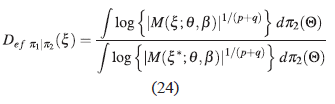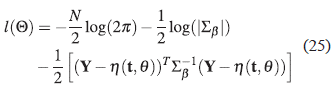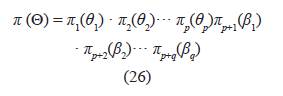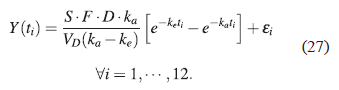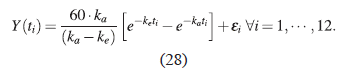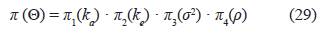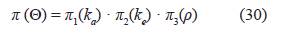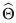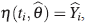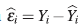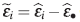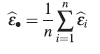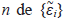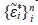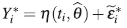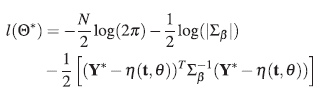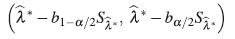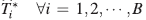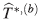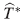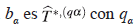Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. INTRODUCCIÓN
Cuando se mencionan los diseños óptimos se tiene una variedad de definiciones unas más técnicas que otras, que al final apuntan a lo mismo, pero no se explica de manera clara para que sirven los diseños óptimos, pues bien, un diseño óptimo, puede facilitar el proceso de recolección de datos y posterior análisis de datos, lo que lleva finalmente a conclusiones confiables y reproducibles de una manera rentable a la hora de hacer un experimento.
El gran avance de los diseños óptimos se debe a las importantes contribuciones hechas principalmente por Kiefer (1959) [1] y Kiefer y Wolfowitz (1960) [2] quienes desarrollaron procedimientos computacionales útiles para encontrar diseños óptimos en problemas de regresión, además sugirieron teorías para cuando el interés recae en uno o varios coeficientes de regresión. Posteriormente varios autores como Fedorov (1972) [3], Pukelsheim (1993) [4], entre otros, en sus libros, trataron e hicieron contribuciones en temas relacionados con diseños óptimos de experimentos. Muchos trabajos de diseños, hasta ahora, se centran en modelos lineales, sin embargo, gran variedad de fenómenos naturales que existen se describen a partir de modelos no lineales. La forma general supuesta para dicho modelo no lineal se presenta en la ecuación (1).
donde se supone que la respuesta, Y, se puede modelar por una función no lineal η(t i , θ ), donde ti es el valor de la variable explicativa en el i-ésimo individuo o unidad experimental (i=1,2,... ,N) y ε i es una variable aleatoria con distribución normal con media cero y varianza constante.
Para este tipo de modelos no lineales se destacan los aportes de Box y Lucas (1959) [5] quienes aplicaron el criterio de D-optimalidad usando un argumento geométrico para la obtención de diseños de m puntos de un modelo de m parámetros, que representaba la reacción química de tres sustancias. Años más tarde Box y Hunter (1965) [6] hacen valiosos aportes en los diseños óptimos para modelos no lineales utilizando un método secuencial para la estimación óptima de los parámetros del modelo de tal forma que ésta fuera lo suficientemente precisa.
Usualmente, cuando se construye un diseño óptimo para modelos de regresión no lineales en el vector de parámetros θ (ver 1), se supone de antemano que los errores son incorrelacionados, esto conlleva a que cuando se calcula la matriz de información de Fisher asociada al diseño, dependa de este vector de parámetros desconocido, de esta manera la construcción de un diseño óptimo para este proceso depende del vector de parámetros, por lo cual se plantean diferentes enfoques para la construcción de diseños óptimos. A uno de estos enfoques se le denomina diseños óptimos locales introducido por Chernoff (1953) [7], el cual consiste en asignarle un valor a priori θ 0 muy θ 0 es determinado por el investigador a partir de experiencias previas en experimentos similares o tomando a θ 0 como un estimador de θ. Algunos autores como Ford, Torsney, y Wu (1992) [8], O’Brien (1992) [9], Dette, Melas, y Wong (2005) [10], entre otros, han utilizado este procedimiento para construir diseños óptimos. Otro enfoque para este problema, propuesto por Pronzato y Walter (1985) [11] y Chaloner y Larntz (1989) [12], es utilizar el conocimiento previo que se tiene acerca de θ a partir de la escogencia de una distribución a priori п, la cual se incorpora en el criterio de optimalidad, este procedimiento es conocido en la literatura de diseños óptimos como criterio de optimalidad Bayesiano, o también conocido como diseños óptimos promediados por una distribución a priori.
En el caso de los modelos no lineales con observaciones correlacionadas, es decir para el vector ε = (ε 1 , ε 2 , . . . , ε N )T , donde ε ~ N N (0, Σ β ), la matriz de información asociada a un diseño, además de depender del vector de parámetros θ, también depende de otro vector de parámetros β de q componentes, asociado a la estructura de correlación del término de error y la matriz de información de Fisher. Esta última es una función que depende tanto del diseño como de los dos vectores de parámetros, ver [13]. Para optimizar un funcional de dicha matriz, se escoge el criterio D-optimalidad, el cual consiste en la maximización del determinante de ésta. El diseño D-óptimo depende Θ T = ( θ T , β T ) y es útil en la medida de que tan acertada sea la escogencia de los valores locales. En este tipo de problemas, autores como Ucinski y Atkinson (2004) [14], Amo-Salas, López-Fidalgo, y López-Ríos (2012) [15], Campos- Barreiro y López-Fidalgo (2015) [16], han obtenido diseños óptimos e incluso han implementado nuevos criterios para la obtención de los diseños. Una forma de evitar la dependencia de los valores locales en la construcción de los diseños óptimos es la incorporación de distribuciones a priori en el criterio de optimalidad y por tanto el diseño resultante depende de la escogencia de la distribución a priori. En este artículo se implementa un procedimiento general para hallar diseños óptimos bayesianos para modelos no lineales en presencia de observaciones correlacionadas, para encontrar estos diseños se utiliza el método de Monte Carlo que seaborda en secciones posteriores, luego el análisis realizado en este artículo se hace considerando el modelo biexponencial que describe la cinética de un fármaco en el organismo y para cada una de la estructuras de correlación propuestas para este modelo se procede a comparar los diseños hallados a través de distribuciones a priori previamente especificadas con un diseño de referencia mediante el cálculo de la eficiencia.
2. Diseños óptimos para modelos no lineales
2.1 Modelo de regresión y el diseño
Los modelos de regresión no lineal proporcionan una herramienta importante para describir la relación entre una variable respuesta Y a través de k-variables explicativas y tienen muchas aplicaciones en ingeniería, física, biología, economía, medicina, entre otras disciplinas [17]. Dicho modelo de regresión no lineal en los parámetros es de la forma:
o en forma matricial el modelo de regresión no lineal se reescribe como:
donde θ ∈ ℝ p un vector de p parámetros desconocidos, Y = (Y (t 1 ), . . . ,Y (t N )) T , t = (t 1 , ... ,t N ), η(t , θ) = [η(t 1 , θ), ... , η(t N , θ)] T , donde η(t i , θ ) es una función de tipo no lineal en θ, t i es el valor de la variable explicativa en el i-ésimo individuo o unidad experimental (i=1,2,. . . ,N) y toma valores en el espacio del diseño χ ⊆ ℝ y ε = (ε 1 , ε 2 , ... , ε N )T es un vector de errores, donde ε ∼ N N (0, Σ β ), β es un vector con q componentes asociada a la estructura del error.
Un diseño ξ se define como una medida de probabilidad con soporte finito sobre el espacio del diseño χ y se representa por:
donde los {t 1 . . .t k } son conocidos como k puntos de soporte distintos del diseño a muestrear, son elementos del espacio del diseño χ con frecuencias (o pesos) aproximadamente proporcionales a w 1 , w 2 ,..., w k donde w i = ξ (t i ) y w i > 0 para i = 1, . . ., k; tal que Σ i w i = 1. Los w i indican la proporción de corridas experimentales que se deben hacer en cada punto del soporte. De la expresión en (4) se desprenden dos tipos de diseños:
Diseño Exacto: El diseño es exacto si los pesos w i = r i /N, con r i enteros y representan el número de réplicas a realizarse en ti y Σ i r i = N.
Diseño aproximado o continuo: En este caso los pesos w i son cualesquier número entre 0 y 1, “es decir”, 0 < w i ≤ 1 para i = 1, . . . , k, por lo cual no se hace ninguna restricción a los pesos de ser números racionales [18].
2.2 Estructura de correlación
Considere el modelo de regresión no lineal en (3) expuesto en la sección 2.1, donde los supuestos para este modelo de regresión son los siguientes: Para observaciones correlacionadas ε ∼ N N (0, Σ β ), β es un vector con q componentes asociada a la estructura del error y Σ β está dado por:
con
donde c (•, β) es llamada función de covarianza. Esta función se supone continuamente diferenciable en el espacio parametral [13], el vector β representa los parámetros de la función de covarianza con β ∈ ℝ q .
En [19] reescriben la ecuación (6), con el fin de facilitar los cálculos al utilizar la matriz de información de Fisher.
donde β T = (σ 2 , ρ T ) con σ 2 ∈ ℝ, ρ ∈ ℝ q−1 parámetros desconocidos en (7).
De esta manera la ecuación (5) se expresa como:
Las estructuras de covarianzas son funciones que tratan de explicar en cierto modo el grado de correlación que existe entre los datos de un determinado experimento. En este trabajo se utilizan las siguientes estructuras de correlación o funciones de covarianza:
Función exponencial
Función Kernel 1
Función de Cauchy 1
La estructura de covarianza en (9) fue tratada por [15] con el fin de estudiar modelos farmacocinéticos anidados, mientras que las estructuras de covarianza en (10) y (11) fueron tratadas por [20] para todo tipo de modelos en presencia de observaciones correlacionadas.
En caso de tener datos, una forma de verificar si los parámetros de la función de covarianza son significativos o no, es mediante el criterio de razón de verosimilitud [21].
2.3 Matriz de información
Para cada diseño ξ se define la matriz de información de Fisher de acuerdo con las siguientes condiciones:
(a) Si en (2) los errores tienen la siguiente estructura ε ∼ N N (0, σ 2 I) la matriz de información de Fisher está dada por:
donde
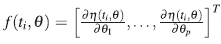; para i = 1, 2, . . . , k en este caso la matriz de información depende del vector de parámetros θ.
(b) Teorema 2.1. Si en el modelo en (3) los errores tienen la siguiente estructura ε ∼ N N (0, Σ β ) y ξ = {t 1 ,t 2 , . . . ,t N } es un diseño exacto de N-puntos, entonces la matriz de información de Fisher está dada por:
donde las matrices M 11 y M 22 se definen a continuación
La matriz de información de Fisher es una matriz particionada, en donde la diagonal principal de esta matriz está conformada por submatrices cuadradas que dependen de los vectores θ, β y ξ. La matriz de información en (13) fue expuesta por [13] quien consideró un modelo no lineal donde los errores presentaban una estructura de correlación.
Corolario 2.1. Si en el modelo 3, Σ β = σ 2 A ρ , entonces M 11 y M 22 están dadas por:
2.4 Criterio D-optimalidad
El criterio D-optimalidad es un método utilizado para hallar diseños que permite estimar de manera óptima los parámetros del modelo, este criterio se basa en minimizar el volumen del elipsoide de confianza, asociado a la estimación de máxima verosimilitud de los parámetros del modelo especificado en (2).
El criterio D-optimalidad se define como el siguiente funcional asociado a un diseño:
donde p: es el número de parámetros del modelo.
El diseño que resulta de maximizar la expresión en (14) se conoce como diseño D-óptimo.
El criterio D-optimalidad, cuando los errores están correlacionados, se define como el siguiente funcional:
Un diseño ξ* es D-óptimo si maximiza (15), esto equivale a tener un diseño que minimice:
Con Ψ un funcional real y |M| denota el determinante de la matriz M, según lo afirmado por [18], es más útil el uso de funciones convexas como el logaritmo natural.
3. DISEÑOS ÓPTIMOS BAYESIANOS
En la teoría de los diseños óptimos para modelos no lineales en el vector de parámetros, cuando se calcula la matriz de información de Fisher asociada al diseño ξ, ésta depende de dos vectores de parámetros, ver (13). Para evitar dicha dependencia se consideran distribuciones a priori π para Θ T = (θ T , β T ) y se incorpora al criterio de optimalidad, resultando de esta manera un criterio denominado Bayesiano. Un diseño ξ es Ψ- óptimo Bayesiano con respecto a la distribución a priori π y se denota como Ψ π - óptimo, si maximiza a:
En particular, un diseño ξ* es D-óptimo Bayesiano con respecto a una distribución a priori π para el vector de parámetros Θ T = (θ T , β T ) y se denota como D π -óptimo si maximiza a:
En ocasiones, es difícil maximizar la expresión (17), por lo cual se recurre a maximizar el logaritmo de ésta como se muestra en (18).
Se puede mostrar que la expresión dada en (18) se puede reescribir, usando (15) y el Corolario 2.1, para más detalle ver la página 28 de la tesis en [22]:
donde
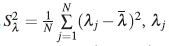es el j-ésimo valor propio de la matriz
.
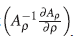Para calcular la integral en (18), ésta se calcula usando el método de Monte Carlo que es un método numérico que sirve para calcular integrales que no se pueden resolver analíticamente, este procedimiento se fundamenta en la simulación de variables aleatorias que son generadas del programa estadístico R [23], el método se expone a continuación.
Sea Nsim el número de simulaciones, que corresponde a la cantidad de valores de Θi que se van a generar de una distribución de probabilidad específica π(Θ) para cada uno de los parámetros del vector de parámetros Θ. Por la ley débil de los grandes números, se tiene que para la distribución π(Θ) y para la función log|M(ξ; Θi)| 1/(p+q) .
donde la expresión
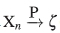denota que la sucesión de variables aleatorias converge en probabilidad a una constante ζ cuando n tiende a infinito.
Y además por definición de esperanza para distribuciones continuas de probabilidad
En otras palabras, de las expresiones dadas en (20) y (21) indican que
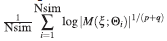converge en probabilidad al criterio Dπ -optimalidad.
Para saber el valor de Nsim apropiado para calcular la integral usando el método de Monte Carlo, se elige una distribución a priori y posteriormente se fijan los valores tanto del diseño como de los parámetros de la integral en (18) y se procede a calcular esta integral vía Monte Carlo utilizando los siguientes valores para Nsim: 1000, 2000, 5000, 7000, 10000, 15000. Y se observa que la integral se estabiliza o se aproxima al valor real cuando Nsim toma un valor de 10000, por tal motivo se decide trabajar con Nsim = 10000.
3.1 Eficiencia de un diseño
Una forma de medir la eficiencia de un diseño ξ, con respecto a un diseño Ψ-óptimo ξ*, es utilizando el cociente del criterio de optimalidad evaluado tanto en ξ como en ξ*, es decir,
donde 0 < Ψef (ξ) ≤ 1. Valores cercanos a uno de la eficiencia para los diseños ξ* Ψ-óptimo y el diseño ξ, significa que el diseño ξ es casi equivalente a ξ*, es decir, que los dos diseños tienen casi las mismas propiedades en cuanto a eficiencia. Según [18], la D ef (ξ) en el caso de D-óptimo local, se puede interpretar como el número de réplicas requeridas del diseño para que sea tan eficiente como el diseño D-óptimo.
Dadas dos distribuciones a priori π 1 y π 2 para Θ, se define la eficiencia del diseño ξ - Ψ π1 -óptimo con respecto al diseño ξ*- Ψ π2 -óptimo denotado por Ψ ef π1|π2 (ξ) como:
Donde la distribución a priori π 2 es la distribución de referencia.
Para el criterio D-optimalidad se define la D ef π1|π2 (ξ) como:
La D ef π1|π2 (ξ) suministra la información de que tan eficiente es el diseño ξ en comparación con el diseño ξ*.
3.2 Estimación de los parámetros asociados al modelo y a la función de covarianza
En esta sección se da una serie de pasos para estimar los vectores de parámetros asociados tanto al modelo no lineal como a la función de covarianza propuesta.
Se elige el conjunto de datos y el modelo no lineal Y (t i ) = η(t i , θ) + ε i , definido en (2), que describe el comportamiento de dichos datos.
Se estima el vector de parámetros θ del modelo no lineal utilizando los datos, esto se hace usando la función nls del R [23].
Si los datos son tomados de un mismo individuo, existe una posible correlación entre ellos, por ende, se proponen funciones de covarianzas de la forma Cov(ε(t i ), ε(t j )) = c (|t i − t j |, β), definida en (6).
Se estima el vector de parámetros ΘT = ( θ T , β T ), conformado por los parámetros tanto del modelo no lineal como de la función de covarianza, esta estimación se hace vía máxima verosimilitud dada por la ecuación (25):
mediante la función nlminb del R [23]. Esta función requiere de valores iniciales por lo cual se utiliza Θ T ini = (θ T est , β T tan ), donde θ T es es el vector de parámetros estimado en el paso 2 y β T tan es el vector de parámetros por tanteo, es decir, formado por valores asignados al azar.
Otra forma alternativa de encontrar o de tener una idea de cuáles son los valores del vector de valores iniciales Θ T ini , es mediante la función DEoptim del R [23], que es un algoritmo genético de evolución diferencial que sirve para maximizar o minimizar funciones, este algoritmo a la hora de optimizar parte de unos valores aleatorios, y además el algoritmo requiere mucho tiempo para optimizar dichas funciones.
Una vez estimado el vector de parámetros β, se efectúa una prueba de hipótesis con la intención de saber si los parámetros de la función de covarianza son significativos o no, en el caso en que no sean significativos quiere decir que la función de covarianza seleccionada no modela la correlación entre los datos por tanto se descarta y se selecciona otra función de covarianza factible.
3.3 Metodología para hallar los diseños D-óptimos Bayesianos
Para hallar diseños D-óptimos bayesianos o Dπ - óptimos, se utiliza la siguiente metodología
1. Primero se construyen intervalos de confianza bootstrap enunciado en [21] adaptado por los autores para observaciones correlacionadas (ver Apéndice 6.1), para cada uno de los elementos del vector de parámetros estimados
.
2. Se considera la distribución uniforme como la primera distribución factible al rango de variación de cada uno de los elementos del vector de parámetros y se toman los extremos del intervalo de confianza bootstrap como el intervalo donde está definida la distribución uniforme para cada uno de los parámetros del vector
.
3. Con el propósito de comparar los diseños se consideran otras distribuciones a priori factibles al rango de variación de cada uno de los elementos del vector de parámetros Θ. Y con el fin de que los diseños sean comparables con los diseños obtenidos con la distribución uniforme se hallan los parámetros de las nuevas a priori igualando la media y la varianza de la distribución uniforme con las respectivas media y varianza de la distribución elegida, este proceso se hace para cada uno de los elementos del vector de parámetros Θ.
4. Con las distribuciones a priori para cada parámetro, obtenidas en la parte 3 y bajo independencia, se halla la distribución apriori conjunta, dada en:
esta a priori conjunta se reemplaza en el criterio D-optimalidad dado en (18).
5. Usando la función nlminb del R [23], el diseño hallado es Dn-óptimo si maximiza a (18) junto con la a priori conjunta especificada en el paso anterior.
6. Finalmente, para cuantificar el efecto de las distribuciones a priori en los diseños óptimos hallados, se hallan las eficiencias para cada uno de los diseños tomando como referencia a los diseños que se encontraron con la distribución uniforme, estas comparaciones se hacen bajo la misma función de covarianza.
4. CASO DE ESTUDIO: MODELO BIEXPONENCIAL
El siguiente conjunto de datos tomado de [24], representa la concentración de lipoamida (ácido lipoico) en un paciente sano después de administrarle una dosis de 120 mg de este medicamento vía oral antes de desayunar. Se tomaron muestras de sangre en diversos momentos y se analizaron para detectar el efecto de la lipoamida en el organismo.
Tabla 1 Concentración de lipoamida
| Tiempo | Concentración |
|---|---|
| (hora) | |
| 0.0 | 0.0 |
| 0.2 | 38.1 |
| 0.4 | 50.6 |
| 0.6 | 54.1 |
| 0.8 | 54.3 |
| 1.0 | 53.3 |
| 1.2 | 52.0 |
| 2.0 | 46.3 |
| 4.0 | 34.4 |
| 10.0 | 14.1 |
| 15.0 | 6.7 |
| 24.0 | 1.8 |
En modelo que describe la concentración de lipoamida en distintos momentos del tiempo está dado por:
donde los parámetros del modelo son kα y ke son las constantes de absorción y eliminación del medicamento, la dosis inicial es D = 120 mg, el factor de sal se toma como S = 1 y el cociente entre el factor de biodisponibilidad F y el volumen de distribución del medicamento VD está dado por F/VD = 1/2, estos valores son determinados previamente por el investigador que está haciendo el estudio, de modo que el modelo en términos de los valores conocidos queda de la siguiente forma:
Las estimaciones de los parámetros del modelo no lineal fueron estimados siguiendo los pasos 1 y 2 descritos en la sección 3.2. Los valores se muestran en la Tabla 2.
De la tabla anterior se observa que la estimación de los parámetros del modelo (28) son altamente significativos, lo que indica que este modelo es el adecuado para modelar la concentración de lipoamida en el cuerpo con respecto al tiempo.
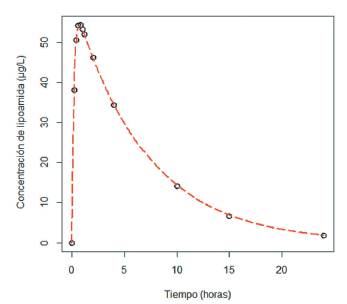
El modelo ajustado para el conjunto de datos que describe la concentración de lipoamida, se muestra en la siguiente figura.
Como los datos son tomados de un mismo individuo, se requiere de una función que exprese el grado de correlación entre estas observaciones, para ello se consideran las funciones de covarianzas expuestas en (9), (10) y (11).
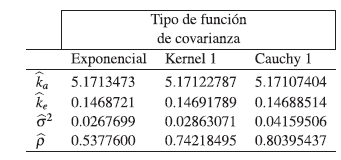
Para ello se estiman los parámetros del modelo y los parámetros de las funciones de covarianzas consideradas usando la función de verosimilitud como se muestra en la siguiente tabla
4.1 Diseños para distribuciones a priori
Una vez encontrados los diseños con los parámetros estimados, se eligen distribuciones a priori para estos, debido a que las estimaciones de los parámetros fueron positivas con cualquier función de covarianza tratada, se consideran distribuciones a priori donde éstas toman valores en un subconjunto de los reales positivos o distribuciones donde su dominio sea un conjunto positivo. En este artículo se utilizan tres distribuciones a priori distintas.
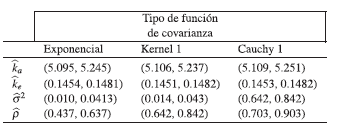
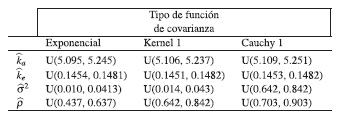
La primera distribución a priori pensada para cada uno de los parámetros fue la distribución Uniforme, debido a la facilidad que tiene esta distribución para la elicitación de los extremos del intervalo de variación de dicha distribución, es decir se puede averiguar entre qué valor mínimo y máximo se encuentra cada parámetro. Para propósitos ilustrativos, se tomaron como extremos del intervalo de la distribución uniforme, los extremos de los intervalos de confianza bootstrap, a un 95 % de confianza, dados en la Tabla 4.
Luego de obtener los intervalos de confianza bootstrap, para cada parámetro y cada función de covarianza, se construye la distribución a priori uniforme como ya antes se ha mencionado, este procedimiento que se utilizó sirve para justificar de manera clara y precisa la escogencia de los extremos de la distribución uniforme, en la siguiente tabla se muestra la a priori uniforme para los parámetros.
Teniendo en cuenta las distribuciones a priori π1(ka), π2(ke), π3(σ2), π4(ρ), que son las distribuciones uniforme expuestas en la tabla 5, se considera la distriución a priori conjunta uniforme como el producto de estas cuatro distribuciones a priori, es decir:
donde ΘT = ( ka, k, σ2, ρ) y además se observó que σ2 no tiene ninguna influencia en el criterio (ver colorario 2.1 y la ecuación (16)), esto quiere decir que si se supone una a priori para σ2 el valor de la integral sobre este parámetro es igual a 1, por ende, la distribución conjunta en (29) queda especificada de la siguiente forma:
Se maximiza la función dada en (18) usando un programa elaborado por los autores en el software estadístico R [23]. Allí se tiene en cuenta cada una de las diferentes distribuciones a priori para hallar, vía el método de Monte Carlo y optimización, los diseños óptimos y las eficiencias reportadas entre paréntesis en las tablas 8, 9 y 10.
Adicionalmente, con el fin de determinar el efecto que tiene la elección de la distribución a priori, se consideró la distribución Gamma (α, β) y la distribución Lognormal (μ, s), como distribuciones factibles para cada uno de los elementos del vector de parámetros Θ. Para los parámetros de estas distribuciones se determinaron usando el procedimiento descrito a continuación:
Se supone que la media de la distribución uniforme de la tabla 5 es igual a la media de la distribución Gamma y la varianza de la uniforme igual a la varianza de la Gamma (ver Tabla 6), lo anterior conduce al siguiente sistema de ecuaciones:
Tabla 6 Sistemas de ecuaciones cuando se iguala la media de la distribución uniforme a la media de la distribución Gamma y la varianza de la Uniforme a la varianza de la Gamma
Tabla 7 Sistemas de ecuaciones cuando se iguala la media de la distribución uniforme a la media de la distribución Lognormal y la varianza de la Uniforme a la varianza de la Lognormal
Resolviendo las ecuaciones de la Tabla 6, se obtienen las siguientes densidades:
Para la función de covarianza Exponencial
kα ∼ Gamma(14255.41, 0.0003626692)
ke ∼ Gamma(36005.36, 0.000004077171)
ρ ∼ Gamma(86.5107, 0.006207325)
Para la función de covarianza Kernel 1
kα ∼ Gamma(18701.3, 0.0002765316)
ke ∼ Gamma(25535.4, 0.0009179732)
ρ ∼ Gamma(165.1692, 0.004492363)
Para la función de covarianza Cauchy 1
kα ∼ Gamma(15968.5, 0.0003243887)
ke ∼ Gamma(31171.65, 0.000004709088)
ρ ∼ Gamma(193.4427, 0.0041511)
Una vez obtenidas las distribuciones a priori π1(kα), π2(ke), π3(ρ) para cada parámetro y cada función de covarianza, se considera la distribución a priori conjunta Gamma como el producto de estas tres distribuciones a priori, ver la expresión (30)
Con esta nueva distribución a priori conjunta se encuentran los diseños D-óptimos y las eficiencias reportadas entre paréntesis en las tablas 8, 9 y 10 usando el mismo procedimiento detallado con la distribución Uniforme en la página 10.
Posteriormente, también se considera que la media de la distribución uniforme sea igual a lamedia de la distribución Lognormal y la varianza de la uniforme igual a la varianza de la distribución Lognormal, como se muestran a continuación:
Solucionando las ecuaciones de la Tabla 7, se encuentra que:
Para la función de covarianza Exponencial
kα ∼ Lognormal(1.64284, 0.00007014604)
ke ∼ Lognormal(−1.91870, 0.00002777331)
ρ ∼ Lognormal(−0.62750, 0.0114929)
Para la función de covarianza Kernel 1
kα ∼ Lognormal(1.64314, 0.00005347057)
ke ∼ Lognormal(−1.91945, 0.00003916083)
ρ ∼ Lognormal(−0.3014241, 0.006036144)
Para la función de covarianza Cauchy 1
kα ∼ Lognormal(1.64477, 0.00006262134)
ke ∼ Lognormal(−1.91877, 0.00003207979)
ρ ∼ Lognormal(−0.2219787, 0.005156173)
Una vez obtenidas las distribuciones a priori π1(kα), π2(ke), π3(ρ) para cada parámetro, se considera la distribución a priori conjunta Lognormal para cada función de covarianza como el producto de estas tres distribuciones a priori, ver la expresión (30)
Finalmente, se hallan los diseños D-óptimos y las eficiencias reportadas entre paréntesis en las tablas 8, 9 y 10 usando la nueva distribución a priori.
Tabla 8 Diseños encontrados utilizando la función de covarianza exponencial y se reporta el valor de la eficiencia del respectivo diseño con relación al diseño óptimo obtenido con la distribución uniforme, en paréntesis. Función covarianza Exponencial
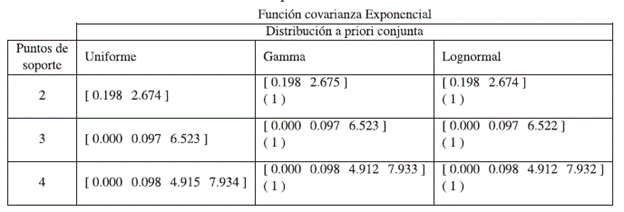
Tabla 9 Diseños encontrados utilizando la función de covarianza kernel 1 y se reporta el valor de la eficiencia del respectivo diseño con relación al diseño óptimo obtenido con la distribución uniforme, en paréntesis.
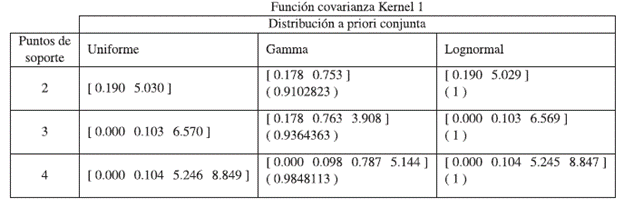
Tabla 10 Diseños encontrados utilizando la función de covarianza Cauchy 1 y se reporta el valor de la eficiencia del respectivo diseño con relación al diseño óptimo obtenido con la distribución uniforme, en paréntesis.
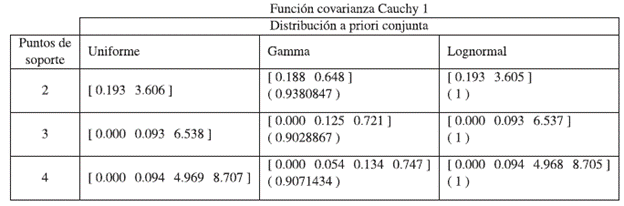
Para hacer las comparaciones se toma como referencia los diseños hallados por medio de la distribución a priori Uniforme, de esta forma, se observa que si se considera la función de covarianza exponencial de la Tabla 8, las eficiencias de los diseños obtenidos con las diferentes distribuciones a priori son iguales a 1, lo que quiere decir que a la hora de estimar el vector de parámetros se obtienen los mismos resultados si se utiliza cualesquiera de los tres diseños hallados con sus respectivas a priori. Ahora si se considera la función de covarianza Kernel 1 de la Tabla 9, se observa que las eficiencias de los diseños hallados cuando se usa la distribución a priori Gamma dieron los siguientes resultados 0.9102, 0.9364 y 0.9848 para diseños de dos, tres y cuatro puntos de soporte respectivamente, mientras que cuando se emplea la distribución a priori Lognormal las eficiencias siguen siendo iguales a 1. Por último, si se trabaja con la función de covarianza Cauchy 1 de la Tabla 10, se nota que las eficiencias "cuando se emplea la distribución a priori Gamma" fueron de 0.938, 0.9028 y 0.9007 para diseños de dos, tres y cuatro puntos de soporte y las eficiencias para cuando se usa la distribución Lognormal también dieron iguales a 1.
CONCLUSIONES
De acuerdo al procedimiento propuesto para encontrar diseños D-óptimos bayesianos se evidencia que si hay efecto a la hora de considerar distribuciones a priori en la obtención de los diseños, aunque este efecto depende de la función de covarianza con la que se esté trabajando, puesto que si se considera la función de covarianza exponencial no hay efecto en considerar distribuciones a priori para obtener los diseños óptimos. Pero si se tiene en cuenta las funciones de covarianza Kernel 1 o Cauchy 1 se observa diferencia entre los diseños hallados mediante la distribución a priori Uniforme y la distribución a priori Gamma, esto también se ve reflejado en los valores de las eficiencias.
