1 Introducción
En 1933, Kuratowski 12 utilizó la teoría de ideales sobre espacios topológicos para introducir una generalización de la clausura de un conjunto, denominada la función local de un conjunto con respecto a un ideal y a una topología. Dado un espacio topológico (X, τ ) e I un ideal topológico sobre X, para cada subconjunto A de X se define la función local de A con respecto a I y τ, como el conjunto A* = {x G X : U n A G I para cada U G τ tal que x G U}. Esta generalización fue de gran utilidad para definir el concepto de operador clausura de Kuratowski C/*, el cual induce una topología τ* que es más fina que la topología τ. En 1992, Jankovic y Hamlett 9, introducen la noción de conjunto I-abierto vía función local A - A*, la cual es independiente de la noción de conjunto abierto y es una generalización del concepto de conjunto pre-abierto dado por Mashhour et al. 15. El estudio de conjuntos abiertos o cerrados mediante la noción de espacios topológicos dotado de ideales es un tema que los topologistas han estudiado y todavía siguen estudiando sobre diferentes campos de la topología general. En el 2019, Granados 5 estudió una variante de continuidad a través de los conjuntos a ai-abiertos en espacios topológicos dotado de ideales. En el año 2020, se estudiaron e introdujeron nuevos conjuntos y conceptos sobre espacios topológicos dotados de ideales, Nestor Pachon 17 introdujeron las nociones de espacios P- Hausdorff, P-regular y P-normal sobre espacios de ideales. Por otro lado, Premkumar y Rameshpandi 18, definen nuevos conjuntos generalizados sobre espacios nano topológicos ideales.
Por otro lado, el estudio de conjuntos pre regulares inició en el 2018 cuando Jeyanthi y Nalayini 11 definieron en su artículo el conjunto pre regular sp-abierto, donde posteriormente en el 2020, Granados 4 introduce y estudia las nociones de conjuntos pre regular pc-abiertos. En este artículo, se define una nueva noción de conjuntos pre regulares sobre espacios topológicos dotados de ideales, los cuales se llamarán conjuntos pre regular pc-I-abiertos. Además, se muestran algunas de sus propiedades y relaciones existentes entre algunos conjuntos ya conocidos en la literatura. Adicionalmente, se definen nuevas variantes de continuidad y contracontinuidad, y se prueban algunas caracterizaciones sobre espacios pre regular pc-I-conexos, pre regular pc-I-T1, pre regular pc-I-T2 y pre regular pc-I-normal.
2 Conceptos preliminares
En esta sección, se muestran algunas definiciones, proposiciones, lemas y/o teoremas, necesarios para el desarrollo de este artículo, es por esto que las demostraciones de estos mismos serán obviados ya que pueden ser encontradas en las referencias citadas.
Definición 2.1. (12) Un ideal I sobre un espacio topológico (X, τ) es una colección no vacia de subconjuntos de X que satisface las siguientes propiedades:
1.
Si A ∈ I y B ⊂ A, entonces B ∈ I. (Propiedad hereditaria).
Si A ∈ I y B ∈ I, entonces A∪B ∈ I. (Propiedad aditiva).
Observación 1. Observe que si I es un ideal, entonces Ø ∈ I, puesto que Ø ⊂ A para cualquier A ∈ I.
Ejemplo 2.1. Sea X un conjunto no vacío. Las siguientes colecciones son ideales sobre X:
La colección de todos los subconjuntos finitos de X, denotada por
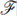 .
.La colección de todos los subconjuntos contables de X, denotada por
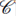 , donde
, donde 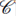 =
=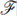 ∪{A : A es enumerable}.
∪{A : A es enumerable}.La colección de todos los subconjuntos nunca densos de X, denotada por
 .
.La colección de todos los subconjuntos cerrados y discretos de X, denotada por
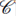
 .
.La colección de todos los subconjuntos magros (o de primera categoría) de X, denotada por
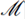
Observación 2. La terna (X, τ, I) dotado por un ideal I, lo llamaremos espacio topológico ideal o espacio topológico dotado de un ideal.
Definición 2.2. (12) Un espacio topológico ideal (X, τ, I) es llamado espacio Hayashi samuels (E.H.S.) si τ ∩I = {/Ø}.
Definición 2.3. (12) Sea (X, τ, I) un espacio topológico ideal. Para cada subconjunto A de X, se define la función local de A con respecto al ideal I y τ de la siguiente manera:
A⋆(I, τ) = {x ∈ X :U ∩A /∈ I, para cada U ∈ τ(x)}, donde τ(x) = {U ∈ τ : x ∈U}
Observación 3. En el desarrollo de este articulo, escribiremos A⋆ en vez de A* (I, τ).
Definición 2.4. (10) Sea (X, τ, I) un espacio topológico ideal. Para cada subconjunto A de X, se define Cl*(A) como la unión de A con A*, es decir Cl*(A) = A∪A*.
Teorema 2.1. (10) Cl* es un operador clausura de Kuratowski.
Observación 4. En virtud del teorema 2.1, si (X, τ, I) es un espacio topológico ideal, denotamos por τ* a la topología generada por Cl*, esto es, τ* ={U ⊂X :Cl*(X−U)=X−U}. Los elementos de τ* son llamados τ*-abiertos y el complemento de un τ*-abierto es llamado τ*-cerrado.
Además, todo conjunto abierto en τ es un conjunto τ*-abierto, pero lo contrario no se cumple siempre.
Teorema 2.2. (10) Sea (X, τ, I) un espacio topológico ideal y A ⊂ X, donde I = { Ø }, entonces Cl*(A) =Cl(A).
Definición 2.5. Sea A un subconjunto del espacio topológico (X, τ), entonces A es:
Semi-abierto13, si A ⊆Cl(Int(A)).
Semi-I-abierto8, si A ⊆Cl*(Int(A)).
b-abierto3, si A ⊆Cl(Int(A))∪Int(Cl(A)).
b-I-abierto6, si A ⊆ Cl*(Int(A))∪Int(Cl*(A)).
β-abierto14, si A ⊆Cl(Int(Cl(A))).
β-I-abierto7, si A ⊆Cl(Int(Cl*(A))).
Almost I-abierto1, si A ⊆Cl(Int(A*)).
pclA = A∪Cl(Int(A))2.
spintA = A∩Cl(Int(Cl(A)))2.
pcl(spintA) = (A ∪ Cl(Int(A))) ∩ Cl(Int(Cl(A)))2
Proposición 2.1. Para cualquier espacio topológico ideal (X, τ, I), los siguientes enunciados siempre son verdaderos:
Definición 2.6. 4Sea A un subconjunto del espacio topológico (X, τ), A es pre regular pcabierto si A = pcl(spintA) = (A ∪ Cl(Int(A))) ∩ Cl(Int(Cl(A))). El complemento de un conjunto pre regular pc-abierto es un conjunto pre regular pc-cerrado. La colección de todos los conjuntos pre regular pc-abiertos y pre regular pc-cerrados de (X, τ) son denotados por PCO(X, τ) y PCC(X, τ), respectivamente.
3 Conjuntos pre regular pc-I-abiertos
En esta sección, definimos y probaremos algunas propiedades de los conjuntos pre regular pc-I-abiertos, además se muestran algunas relaciones entre los conjuntos definidos en la sección anterior.
Definición 3.1. Sea (X, τ, I) un espacio topológico ideal y A ⊂ X, A es un conjunto pre regular pc-I-abierto, si A = pcl*(spintA) = (A∪Cl*(Int(A)))∩Cl*(Int(Cl*(A))). El complemento de un conjunto pre regular pc-I-abierto es un conjunto pre regular pc-I-cerrado.
La colección de todos los conjuntos pre regular pc-I-abiertos y pre regular pc-I-cerrados son denotados por PCIO(X, τ, I) y PCIC(X, τ, I).
El siguiente ejemplo muestra que las nociones de conjuntos pre regular pc-abiertos y pre regular pc-I-abiertos son independientes:
Ejemplo 3.1. Sea X = {a,b,c} con la topología τ = {/Ø,X,{b,c},{a,c},{c}} y el ideal I = {/Ø,{b}}, entonces la colección de conjuntos pre regular pcabiertos son PCO(X, τ) = {/Ø,X,{b,c},{a,c}} y la colección de conjuntos pre regular pc-I-abiertos son PCIO(X, τ, I) = {/ Ø,X,{b},{a,c}}. Entonces, podemos observar que el conjunto {b} es un conjunto pre regular pc-I-abierto, pero no es un conjunto pre regular pc-abierto y el conjunto {b,c} es un conjunto pre regular pc-abierto, pero no es un conjunto pre regular pc-I-abierto.
Para que los conjuntos pre regular pc-abiertos y pre regular pc-I-abiertos se encuentren relacionados, debe de cumplirse la siguiente condición:
Teorema 3.1. Sea (X, τ, I) un espacio topológico ideal. Si I = { Ø }, entonces si A es un conjunto pre regular pc-I-abierto, si y solo si, A es un conjunto pre regular pc-abierto.
Proof. Sea A un subconjunto del espacio topológico ideal (X, τ, I) tal que I = {}, entonces por el teorema 2.2, Cl*(A) = Cl(A), esto implica que si A es un conjunto pre regular pc-abierto, entonces A = (A ∪ Cl(Int(A))) ∩ Cl(Int(Cl(A))) = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))), así tenemos que A también será un conjunto pre regular pc-I -abierto.
Observación 5. Teniendo en cuenta el teorema anterior, es importante que I = { Ø } para que los conjuntos pre regular pc-abiertos y pre regular pc-I-abiertos este relacionados, de lo contrario ocurrirá lo propuesto en el ejemplo 3.1.
Teorema 3.2. Sea (X, τ, I) un espacio topológico ideal, entonces los siguientes enunciados son ciertos:
Proof. 1. Sea A un conjunto pre regular pc-I-abierto en (X, τ), esto implica que A = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))) ⊂Cl(Int(Cl*(A))), esto prueba que A es un conjunto β-I-abierto.
2. Dado que todo conjunto β-I-abierto es β- abierto y por la parte (1) de este teorema, tenemos que todo conjunto pre regular pc-I-abierto es β-abierto.
El reciproco del teorema anterior no siempre es verdadero, a continuación podemos ver un ejemplo.
Ejemplo 3.2. Sea X = {a,b,c}, con la topología τ = { Ø,X,{a}} y el ideal I = { Ø }, entonces {a,b} es un conjunto β-I-abierto y consecuentemente es β-abierto, pero no es un conjunto pre regular pc-I-abierto.
Teorema 3.3. Si A es un conjunto pre regular pc-I-abierto del espacio topológico ideal (X, τ, I), tal que Int(A) = / Ø y Cl*(A) = A, entonces A es un conjunto semi-abierto.
Proof. Sea A un conjunto pre regular pc-I-abierto, tal que Int(A) = Ø y Cl*(A) = A, entonces tenemos que A = (A ∪ Ø) ∩Cl(Int(A)) = A ∩Cl(Int(A)) ⊂ Cl(Int(A)), por lo tanto A es un conjunto semiabierto.
Proposición 3.1. Si A es un conjunto pre regular pc-I-abierto del espacio topológico ideal (X, τ, I), tal que Int(A) = Ø y Cl*(A) = A, entonces A es un conjunto b-abierto.
Proof. Dado que todo conjunto semi-abierto es b-abierto, y por el teorema 3.3, A es un conjunto semi-abierto, esto implica que A es un conjunto b-abierto.
Teorema 3.4. Si A es un conjunto pre regular pc-I-abierto del espacio topológico ideal (X, τ, I), tal que A ⊂ A*, entonces A es un conjunto almost I-abierto.
Proof. Sea A un conjunto pre regular pc-I-abierto, entonces A=(A∪Cl*(Int(A)))∩Cl(Int(Cl*(A)))= (A ∪ Cl*(Int(A))) ∩ Cl(Int(A ∪ A*)), dado que A ⊂ A*, tenemos que A = (A ∪ Cl*(Int(A))) ∩Cl(Int(A*)) ⊂Cl(Int(A*)), por lo tanto esto implica que A es un conjunto almost I-abierto.
Teorema 3.5. Sea A un conjunto abierto y pre regular pc-I-abierto del espacio topológico ideal (X, τ), entonces A es un conjunto semi-I-abierto.
Proof. Dado que A es un conjunto prer regular pc-I-abierto, tenemos que A = (A∪Cl*(Int(A)))∩Cl(Int(Cl*(A))) ⊂ A ∪Cl*(Int(A)), como A es un conjunto abierto, entonces A ⊆ Cl*(Int(A)), por lo tanto A ∪Cl*(Int(A)) = Cl*(Int(A)), y así A ⊂ Cl*(Int(A)), esto prueba que A es un conjunto semi-I-abierto.
Proposición 3.2. Sea A un conjunto abierto y pre regular pc-I-abierto del espacio topológico ideal (X, τ), entonces A es un conjunto b-I-abierto.
Proof. Por el teorema 3.5 tenemos que A es un conjunto semi-I-abierto, por la proposición 2.1, parte (4), tenemos que A es un conjunto b-I-abierto.
Definición 3.2. Sea A un subconjunto del espacio topológico ideal. Entonces A es un conjunto:
Teorema 3.6. Para cualquier subconjunto A del espacio topológico ideal (X, τ), los siguientes enunciados son equivalentes:
Proof. (1)=⇒(2): Sea A un conjunto pre regular pc-I-abierto, entonces A = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))), por la definición 3.2, parte (1), tenemos que pcl*A = A ∪ Cl*(Int(A)), por lo tanto A = pcl*A∩Cl(Int(Cl*(A))). (2)=⇒(3): Sea A = pcl*A ∩ Cl(Int(Cl*(A))) = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))) = (A ∩ Cl(Int(Cl*(A)))) ∪ (Cl(Int(Cl*(A))) ∩ Cl*(Int(A))), por la parte (2) de la definición 3.2, (spintA)* = A ∩ Cl(Int(Cl*(A))). Además, Cl*(Int(A)) ⊆ Cl(Int(Cl*(A))), esto implica que Cl(Int(Cl*(A))) ∩ Cl*(Int(A)) = Cl*(Int(A)), en consecuencia esto prueba que A = (spintA)* ∪Cl*(Int(A)).
(3)=⇒(1): Sea A = (spintA)* ∪ Cl*(Int(A)) = (A ∩ Cl(Int(Cl*(A)))) ∪ Cl*(Int(A)) = (A ∪Cl*(Int(A))) ∩ (Cl*(Int(A)) ∪ Cl(Int(Cl*(A)))), pero Cl*(Int(A)) ⊆ Cl(Int(Cl*(A))), esto implica que Cl(Int(Cl*(A))) ∪ Cl*(Int(A)) = Cl(IntCl*(A))), en efecto tenemos que A = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))), por lo tanto A es un conjunto pre regular pc-I-abierto.
A continuación mostraremos algunos resultados hallados de los conjuntos pre regular pc-I-abiertos.
Iniciaremos mostrando un contraejemplo donde podemos ver que todo conjunto abierto no es necesariamente un conjunto pre regular pc-I-abierto.
Ejemplo 3.3. Sea X = {a,b,c}, con el ideal I = {Ø,{c}} con la topología τ = {Ø,X,{a},{a,b}}. Entonces la colección de todos los conjuntos pre regular pc-I-abiertos son PCIO(X, τ, I) = {Ø,X}, podemos ver que los conjuntos {a} y {a,b} no son pre regular pc-I-abiertos.
Ahora mostraremos dos contraejemplos que muestran que la unión, la intersección y la diferencia arbitraria de dos conjuntos pre regular pc-I-abiertos no es un conjunto pre regular pc-I-abierto.
Ejemplo 3.4. Sea X = {a,b,c}, con el ideal I = {Ø,{a}} y la topología τ = {Ø,X,{a},{b},{a,b}}. Entonces, la colección de todos los conjuntos pre regular pc-I-abierto son PCIO(X, τ, I) = {Ø,X,{a},{b}}, podemos ver que {a} y {b} son conjuntos pre regular pc-I-abiertos, pero {a} ∪ {b} = {a,b} no es un conjunto pre regular pc-I-abierto.
Ejemplo 3.5. Sea X = {a,b,c}, con el ideal I = {Ø,{a},{c},{a,c}} y la topología τ = { Ø,X,{c},{b,c},{a,c}}. Entonces, la colección de todos los conjuntos pre regular pc-I-abierto son PCIO(X, τ, I) = { Ø,X,{b,c},{a,c}}, podemos ver que {b,c} y {a,c} son conjuntos pre regular pc-I-abiertos, pero {a,c} ∪ {b,c} = {c} no es un conjunto pre regular pc-I-abierto.
Por otro lado, podemos ver que {b,c}−{a,c} = {c}, por el enunciado anterior, concluimos que {c} no es un conjunto pre regular pc-I-abierto.
Teorema 3.7. Sea (X, τ, I) un espacio topológico ideal y A ⊂ X. Si A es un conjunto pre regular pc-I-abierto donde I = {Ø}, entonces el conjunto vacío es el único conjunto que es nunca denso y pre regular pc-I-abierto.
Proof. Sea A un conjunto pre regular pc-I-abierto, como I ={Ø} esto implica que Cl*(A)=Cl(A), y tenemos que, A = (A ∪ Cl*(Int(A))) ∩ Cl(Int(Cl*(A))) = (A∪Cl(Int(A)))∩Cl(Int(Cl(A))) = Ø, si y solo si, A = Ø.
4 Continuidad vía conjuntos pre regular pc-I-abiertos
En esta sección, se introducen y estudian algunas variantes de continuidad sobre los conjuntos pre regular pc-I-abiertos, además se muestran algunas carnetizaciones. En esta sección, τ, σ y ω denotaran espacios topológicos. Además, I, J y K denotaran ideales.
Definición 4.1. Una función f : (X, τ)→(Y,σ,J) es pre regular pc-I-continua, si f −1(V) es un conjunto pre regular pc-I-abierto en (X, τ, I) para cada conjunto V abierto en (Y,σ,J).
Definición 4.2. Una función f : (X, τ, I)→(Y,σ,J) y X es sweca-pre regular pc-I-continua si f −1(V) es un conjunto pre regular pc-I-abierto en (X, τ, I) para cada conjunto V σ*-abierto en (Y,σ,J).
Teorema 4.1. Toda funcion sweca-pre regular pc-I-continua es pre regular pc-I-continua.
Proof. Sea A un conjunto abierto en (Y,σ,J), entonces A es un conjunto σ*-abierto en (Y,σ,J), dado que f es una función sweca-pre regular pc-I-continua, entonces f −1(A) es un conjunto pre regular pc-I-abierto en (X, τ, I), por lo tanto f es una función pre regular pc-I-continua.
Observación 6. El reciproco del teorema anterior no se cumple de forma general, pues todo conjunto σ*-abierto no es necesariamente un conjunto abierto, entonces podrá existir un conjunto σ*- abierto en (Y,σ,J) que no sea pre regular pc-I-abierto en (X, τ, I).
Teorema 4.2. Sea f : (X, τ, I) → (Y,σ,J) y g : (Y,σ,J) → (Z,ω,K) dos funciones, con τ,σ y ω espacios topológicos e I,J y K ideales, entonces los siguientes enunciados son verdaderos:
g ◦ f es pre regular pc-I-continua, si f es pre regular pc-I-continua y g es continua.
g◦ f es sweca-pre regular pc-I-continua, si f es sweca-pre regular pc-I-continua y g continua.
Proof. 1. Sea V un conjunto abierto en Z, como g es una función continua, entonces g−1(V) es un conjunto abierto en Y, dado que f es una función pre regular pc-I-continua, tenemos que f −1(g−1(V)) es un conjunto pre regular pc-I-abierto en X, pero (g ◦ f )−1(V) = f −1(g−1(V)), esto muestra que g ◦ f es una función pre regular pc-I-continua.
La demostración del punto (2), se realiza de manera similar al punto (1).
Teorema 4.3. Para cualquier función f : (X, τ, I)→ (Y,σ,J), tal que la unión arbitraria de conjuntos pre regular pc-I-abiertos en X es un conjunto pre regular pc-I-abierto, entonces los siguientes enunciados son equivalentes:
f es pre regular pc-I-continua.
f −1(B) es un conjunto pre regular pc-I-cerrado en X para cada conjunto cerrado B en Y.
Para cada x ∈ X y cada conjunto V abierto en Y conteniendo a f (x) existe un conjunto pre regular pc-I-abierto U en X conteniendo a x y f (U) ⊂V.
Proof. (1) ⇒ (2): Sea B cualquier subconjunto cerrado en Y, entonces V = Y −B es un conjunto abierto en Y y dado que f es una función pre regular pc-I-continua, f −1(V) es un conjunto pre regular pc-I-abierto de X, pero f −1(V) = f −1(Y − B) = f −1(Y)− f −1(B)=X− f −1(B), por lo tanto f −1(B) es un conjunto pre regular pc-I-cerrado de X.
(2) ⇒ (1): Sea V cualquier conjunto abierto en Y, then B = Y −V es un conjunto cerrado en Y y por hipótesis, tenemos que f −1(B) es un conjunto pre regular pc-I-cerrado de X, pero f −1(B) = f −1(Y −V) = f −1(Y)− f −1(V) = X − f −1(V), por lo tanto f −1(V) es un conjunto pre regular pc-I-abierto de X. Esto muestra que f es una función pre regular pc-I-continua.
(1)⇒(3): Sea x ∈ X y B un conjunto abierto en Y tal que f (x) ∈ B, entonces x ∈ f −1(B) y dado que f es una función pre regular pc-I-continua, f −1(B) es un conjunto pre regular pc-I-abierto en X. Si U = f −1(B), entonces U es un conjunto pre regular pc-I-abierto de X tal que x ∈U y f (U)= f ( f −1(B))⊂B.
(3) ⇒ (1): Sea B cualquier conjunto abierto en Y y x ∈ f −1(B), entonces f (x) ∈ B y por la parte (3) de este teorema, existe un conjunto pre regular pc-I-abierto Ux de X tal que x ∈ Ux y f (Ux) ⊂ B. por lo tanto, x ∈ Ux ⊂ f −1( f (U)) ⊂ f −1(F), en consecuencia f −1(B) = S {Ux : x ∈ f −1(B)}. En conclusión tenemos que f −1(B) es un conjunto pre regular pc-I-abierto de X.
Teorema 4.4. Para cualquier función f : (X, τ, I)→ (Y,σ,J), tal que la unión arbitraria de conjuntos pre regular pc-I-abiertos en X es un conjunto pre regular pc-I-abierto, entonces los siguientes enunciados son equivalentes:
f es sweca-pre regular pc-I-continua.
f −1 (B) es un conjunto pre regular pc-I-cerrado en X para cada conjunto σ*-cerrado B en Y.
Para cada x ∈ X y cada conjunto V σ*-abierto en Y conteniendo a f (x) existe un conjunto pre regular pc-I-abierto U en X conteniendo a x y f (U) ⊂V.
Proof. La demostración de este teorema se realiza de manera similar al teorema 4.3.
Definición 4.3. Un espacio topológico ideal (X, τ, I) es pre regular pc-I-T1 si para cada par de puntos x,y con x ‡y, existe al menos un conjunto pre regular pc-I-abierto que contiene a x o y, pero no a ambos.
Definición 4.4. Una función f : (X, τ)→(Y,σ,J) es pre regular pc-I-irresoluta, si f −1(V) es un conjunto pre regular pc-I-abierto en (X, τ, I) para cada conjunto V pre regular pc-I-abierto en (Y,σ,J).
Teorema 4.5. Sea f : (X, τ, I) → (Y,σ,J) una función pre regular pc-I-irresoluta, con X un espacio pre regular pc-I-T1, entonces Y es un espacio pre regular pc-I-T1
Proof. Supongamos que Y no es un espacio pre regular pc-I-T1. Si para cada par de puntos x,y con x ̸= y tal que U y V son conjuntos pre regular pc-I-abiertos con U ∩V ̸= Ø con x ∈ U y y ∈ V, dado que f es una función pre regular pc-I-irresoluta, f −1(U ∩V) ̸= Ø en X y esto contradice que X es un espacio pre regular pc-I-T1.
Definición 4.5. Un espacio topológico ideal (X, τ, I) es pre regular pc-I-T2, si para cada par de puntos diferentes x,y ∈ X, existen conjuntos pre regular pc-I-abiertos U y V de X tal que x ∈ U, y ∈ V, U ∩V = Ø.
Teorema 4.6. Si f : (X, τ, I) → (Y,σ,J) es una función abierta, inyectiva y pc-I-continua, donde (Y,σ) es un espacio pre regular pc-I-T2, entonces (X, τ, I) es un espacio pre regular pc-I-T2
Proof. Sea A y B dos conjuntos abiertos diferentes en X. Como f es una función abierta e inyectiva, entonces f (A) y f (B) son conjuntos abiertos disyuntos en Y y como (Y,σ,J) es un espacio pre regular pc-I-T2, existen dos conjuntos abiertos G y H de Y tales que f (A) ⊂ G, f (B) ⊂ H y G∩H = Ø. Ahora, dado que f es una función pre regular pc-I-continua, f −1(G) y f −1(H) son conjuntos pre regular p-I-abiertos de X, aunque A ⊂ f −1( f (A)) ⊂ f −1(G), B ⊂ f −1( f (B)) ⊂ f −1(H) y f −1(G) ∩ f −1(H) = f −1(G∩H) = f −1( Ø) = Ø. Esto prueba que (X, τ, I) es un espacio pc-I-T2.
Definición 4.6. Un espacio topológico ideal (X, τ, I) es pre regular pc-I-conexo, si X no puede escribirse como una unión disyunta de dos conjuntos pc-I-abiertos diferentes de vacío.
Teorema 4.7. Para un espacio topológico ideal (X, τ, I), los siguientes enunciados son equivalentes:
(X, τ, I) es pre regular pc-I-conexo.
Ø y X son los únicos conjuntos de X que son al mismo tiempo pre regular pc-I-abiertos y pre regular pc-I-cerrados.
Cada función pre regular pc-I-continua de X es un espacio discreto en Y con al menos dos puntos, es un función constante.
Proof. (1) =⇒(2): Sea B un conjunto de X que es pre regular pc-I-abierto y pre regular pc-I-cerrado, entonces X −B es pre regular pc-I-abierto y pre regular pc-I-cerrado, así X = B∪(X −B), como X es conexo, entonces B = Ø o B = X.
(2) =⇒ (1): Supongamos que X no es pre regular pc-I-conexo y X = U ∪ B, entonces U = X − B, por hipótesis, se tiene que U = Ø o U = X, lo que contradice el hecho de que U y V son no vacíos.
(2) =⇒ (3): Sea f (X, τ, I) → Y una función pre regular pc-I-continua donde Y es un espacio topológico discreto y contiene al menos dos puntos, entonces X se puede escribir como una colección de conjuntos que son a la vez pre regular pc-I-abiertos y pre regular pc-I-cerrados de la forma que { f −1(y) : y ∈ Y}, de esto, se concluye que existe un y0 ∈Y tal que f −1({y0})=X y así, f es una función constante.
(3) =⇒ (2): Sea Z un conjunto de X que es pre regular pc-I-abierto y pre regular pc-I-cerrado. Supongamos que W ‡ Ø y sea f : (X, τ, I) → Y una función pre regular pc-I-continua definida por f (Z) = {y1} y f (X −Z) = {Y2} para y1 ‡y2, con y1,y2 ∈Y. Puesto que f es una función constante, se concluye que X = Z.
Definición 4.7. Una función f : (X, τ, I)→(Y,σ,J) se dice:
Contra pre regular pc-I-continua, si f −1(V) es un conjunto pre regular pc-I-cerrado en X para cada conjunto abierto V en Y.
Contra sweca-pre regular pc-I-continua, si f −1(V) es un conjunto pre regular pc-I-cerrado en X para cada conjunto σ*-abierto V en Y.
Teorema 4.8. Toda función contra sweca-pre regular pc-I-continua es contra pre regular pc-I-continua.
Proof. Sea V un conjunto abierto en Y, entonces V es un conjunto σ*-abierto en Y y puesto que f es contra sweca-pre regular pc-I-continua, tenemos que f −1(V) es un conjunto pre regular pc-I-cerrado de X. Por lo tanto, f es contra pre regular pc-I-continua.
Observación 7. El reciproco del teorema anterior no se cumple de forma general, pues todo conjunto σ*-abierto no es necesariamente un conjunto abierto, entonces puede existir un conjunto σ*- abierto en (Y,σ,J) que no sea pre regular pc-I-cerrado en (X, τ, I), como se puede ver en el siguiente ejemplo.
Ejemplo 4.1. Sea X = {q,w,e}, τ = {Ø,X,{q},{q,w}}, σ = { Ø,X,{e},{w,e}}, I = { Ø,{e}} y J = { Ø,{e},{w,e},{w}}. Entonces, la colección de todos los subconjuntos σ*-abiertos de X es { Ø,X,{e},{w,e},{q},{q,w},{q,w}} y la colección de todos los subconjuntos pre regular pc-I-cerrados de X es { Ø,X,{e},{w,e},{q,e},{w}}. La función identidad f : (X, τ, I) → (X,σ,J) es contra pre regular pc-I-continua, pero no es contra sweca-pre regular pc-I-continua.
Teorema 4.9. Sea f : (X, τ, I) → (Y,σ,J) una función, tal que la unión arbitraria de conjuntos pre regular pc-I-abiertos en X es un conjunto pre regular pc-I-abierto, entonces los siguientes enunciados son equivalentes:
f es contra pre regular pc-I-continua.
f −1(F) es un conjunto pre regular pc-I-abierto en X para cada conjunto cerrado F de Y .
Para cada x ∈ X y cada conjunto cerrado F de Y que contiene a f (x), existe un conjunto pre regular pc-I-abierto U de X que contiene a x y f (U) ⊂ F.
Proof. (1)⇒(2): Sea F cualquier conjunto cerrado en Y, entonces V =Y −F es un conjunto abierto en Y y puesto que f es contra pre regular pc-I-continua, f −1(V) es un conjunto pre regular pc-I-cerrado de X, pero f −1(V) = f −1(Y −F) = f −1(Y)− f −1(F) = X − f −1(F) y por lo tanto, f −1(F) es un conjunto pre regular pc-I-abierto en X.
(2)⇒ (1): Sea V cualquier conjunto abierto de Y, entonces F =Y −V es un conjunto cerrado de Y y por hipótesis, tenemos que f −1(F) es un conjunto pre regular pc-I-abierto en X, pero f −1(F) = f −1(Y −V) = f −1(Y) − f −1(V) = X − f −1(V) y por lo tanto, f −1(V) es un conjunto pre regular pc-I-cerrado en X. Esto demuestra que f es contra pre regular pc-I-continua.
(1)⇒(3): Sea x ∈ X y F un conjunto cerrado en Y tal que f (x) ∈ F, entonces x ∈ f −1(F) y puesto que f es una función contra pre regular pc-I-continua, f −1(F) es un conjunto pre regular pc-I-abierto en X. Si U = f −1(F), entonces U es un conjunto pre regular pc-I-abierto en X tal que x ∈ U y f (U) = f ( f −1(F)) ⊂ F.
(3) ⇒ (1): Sea F cualquier conjunto cerrado en Y y x ∈ f −1(F), entonces f (x) ∈ F y por la parte (3) de este teorema, existe un conjunto pre regular pc-I-abierto Ux de X tal que x ∈ Ux y f (Ux) ⊂ F. Así, x ∈ Ux ⊂ f −1( f (U)) ⊂ f −1(F) y por lo tanto, f −1(F) = S {Ux : x ∈ f −1(F)}. Por lo tanto, concluimos que f −1(F) es un conjunto pre regular pc-I-abierto en X.
Teorema 4.10. Sea f : (X, τ, I) → (Y,σ,J) una función, tal que la unión arbitraria de conjuntos pre regular pc-I-abiertos en X es un conjunto pre regular pc-I-abierto, entonces los siguientes enunciados son equivalentes:
f es contra sweca-pre regular pc-I-continua.
f −1 (F) es un conjunto pre regular pc-I-abierto en X para cada conjunto σ*-cerrado F de Y .
Para cada x ∈ X y cada conjunto σ*-cerrado F de Y que contiene a f (x), existe un conjunto pre regular pc-I-abierto U de X que contiene a x y f (U) ⊂ F.
Proof. La demostración de este teorema se realiza de manera similar al teorema 4.9.
Teorema 4.11. Si f : (X, τ, I)→(Y,σ,J) es una función sobreyectiva contra pre regular pc-I-continua y (X, τ, I) es un espacio pre regular pc-I-conexo, entonces el espacio (Y,σ,J) no es discreto.
Proof. Supongamos que (Y,σ,J) es un espacio discreto y sea A cualquier conjunto propio no vacío en Y. Entonces, A es un conjunto abierto y cerrado en Y y como f es contra pre regular pc-I-continua, tenemos que f −1(A) es un conjunto pre regular pc-I-abierto y pre regular pc-I-cerrado en X. Puesto que (X, τ, I) es un espacio pre regular p-I-conexo, por el Teorema 4.7, los únicos conjuntos de X que son a la vez pre regular pc-I-abiertos y pre regular pc-I-cerrados son Ø y X. Así, f −1(A) = Ø o f −1(A) = X. Si f −1(A)= Ø, entonces esto contradice el hecho que A ̸= Ø y f es sobreyectiva. Si f −1(A) = X, entonces f no es una función. Por lo tanto, (Y,σ,J) no es un espacio discreto.
Teorema 4.12. Un espacio topológico ideal (X, τ, I) es pre regular pc-I-conexo, si cada función contra pre regular pc-I-continua f : (X, τ, I) → (Y,σ,J), donde (Y,σ,J) es un espacio T0, es una función constante.
Proof. Supongamos que (X, τ, I) no es un espacio pre regular pc-I-conexo y cada función contra pre regular pc-I-continua f : (X, τ, I)→(Y,σ,J), donde (Y,σ,J) es un espacio T0 , es una función constante. Puesto que (X, τ, I) no es un espacio pre regular pc-I-conexo, por el Teorema 4.7, existe un subconjunto propio no vacío A de X que es a la vez pre regular pc-I-abierto y pre regular pc-I-cerrado. Sea Y = {a,b} y σ = {Y, Ø,{a},{b}} una topología para Y. Sea f : (X, τ, I)→(Y,σ,J) una función tal que f (A) = {a} y f (X −A) = {b}, entonces f es una función no constante y contra pre regular pc-I-continua tal que (Y,σ,J) es un espacio T0, que es una contradicción. Por lo tanto, (X, τ, I) es un espacio pre regular pc-I-conexo.
Teorema 4.13. Si f : (X, τ, I) → (Y,σ,J) es una función contra pre regular pc-I-continua y (Y,σ,J) es un espacio regular, entonces f es pre regular pc-I-continua.
Proof. Sean x ∈ X y V un conjunto abierto en Y tal que f (x) ∈ V. Puesto que (Y,σ,J) es regular, existe un conjunto abierto W de Y tal que f (x) ∈ W ⊂ Cl(W) ⊂V. Ahora, como f es una función contra pre regular pc-I-continua y Cl(W) es un conjunto cerrado en Y que contiene a f (x), entonces por el Teorema 4.9, existe un conjunto pre regular pc-I-abierto U en X tal que x ∈U y f (U) ⊂Cl(W) ⊂V. Entonces esto muestra que f es una función pre regular pc-I-continua.
Definición 4.8. Un espacio topológico ideal (X, τ, I) se dice pre regular pc-I-normal, si para cada par de conjuntos cerrados disjuntos A y B de X, existen conjuntos pre regular pc-I-abiertos U y V tales que A ⊂U, B ⊂V y U ∩V = Ø.
Teorema 4.14. Si f : (X, τ, I) → (Y,σ,J) es una función cerrada, inyectiva y contra pre regular pc-I-continua y (Y,σ,J) es un espacio ultra normal, entonces (X, τ, I) es un espacio pre regular pc-I-normal.
Proof. Sean A y B dos conjuntos cerrados disjuntos en X. Puesto que f es cerrada e inyectiva, entonces f (A) y f (B) son conjuntos cerrados disjuntos en Y y como (Y,σ,J) es un espacio ultra normal, existen dos conjuntos cerrados y abiertos a la vez G y H en Y tales que f (A) ⊂ G, f (B) ⊂ H y G∩H = Ø. Ahora, como f es contra pre regular pc-I-continua, f −1(G) y f −1(H) son conjuntos pre regular pc-I-cerrados en X y además, A ⊂ f −1( f (A)) ⊂ f −1(G), B ⊂ f −1( f (B)) ⊂ f −1(H) y f −1(G) ∩ f −1(H) = f −1(G ∩ H) = f −1( Ø) = Ø. Esto demuestra que (X, τ, I) es un espacio pre regular pc-I-normal.
Teorema 4.15. Si una función f : (X, τ, I) → (Y,σ,J) es inyectiva contra pre regular pc-I-continua y (Y,σ,J) es un espacio Urysohn, entonces (X, τ, I) es un espacio pre regular pc-I-T2.
Proof. Sean x,y ∈ X tales que x ̸= y. Puesto que f es una función inyectiva, tenemos que f (x) ̸= f (y) y, como (Y,σ,J) es un espacio Urysohn, existen conjuntos abiertos U y V de Y tales que f (x) ∈ U, f (y) ∈ V y Cl(U)∩Cl(V) = Ø. Dado que Cl(U) y Cl(V) son conjuntos cerrados en Y tales que f (x) ∈ Cl(U) y f (y) ∈ Cl(V), la contra pre regular pc-I-continuidad de f garantiza, por el Teorema 4.9, la existencia de dos conjuntos pre regular pc-I-abiertos A y B en X tales que x ∈ A, y ∈ B, f (A) ⊂Cl(U) y f (B)⊂Cl(V). Así, f (A)∩ f (B)⊂Cl(U)∩Cl(V)= Ø, por lo que f (A∩B) = f (A)∩ f (B) = Ø y por lo tanto, A∩B = Ø. Esto demuestra que (X, τ, I) es un espacio pre regular pc-I-T2














