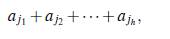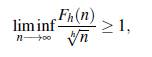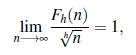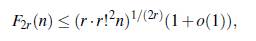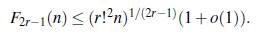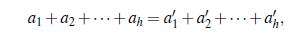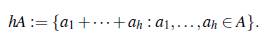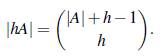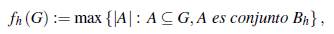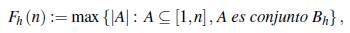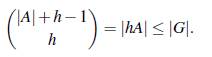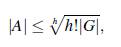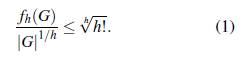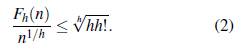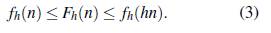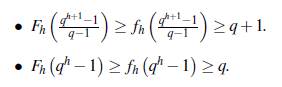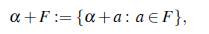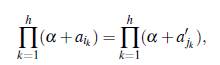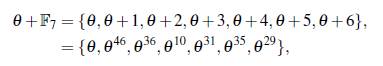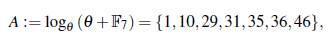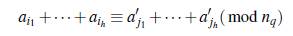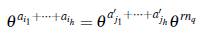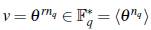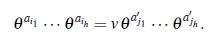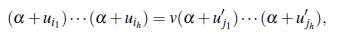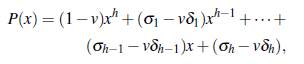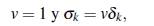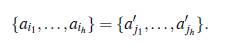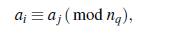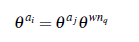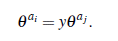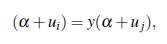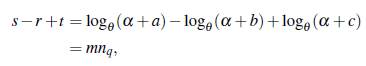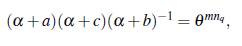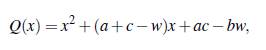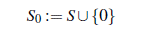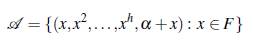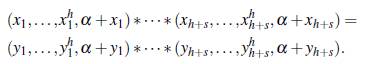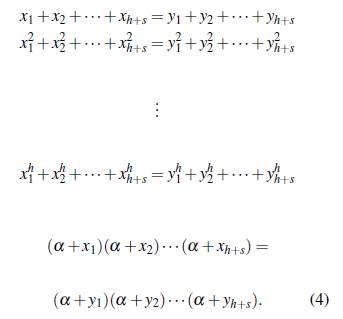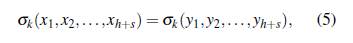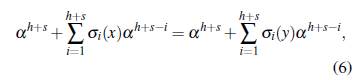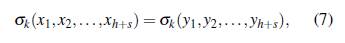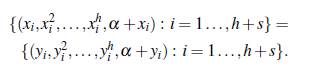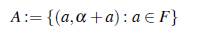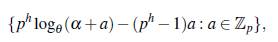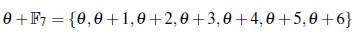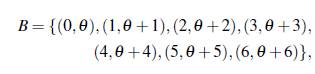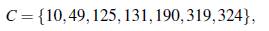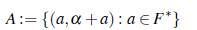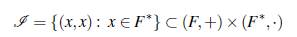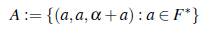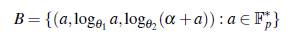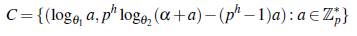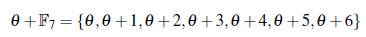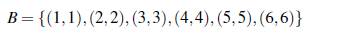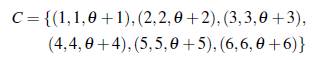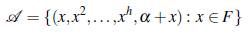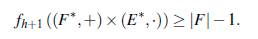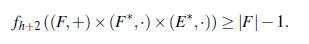1 Introducción
El estudio de conjuntos de enteros con la propiedad que todas las sumas de dos elementos sean distintas, inicia con Simon Sidon en el año de 1932, cuando quiere determinar el máximo cardinal de un conjunto con esta propiedad contenido en los primeros n enteros positivos; a estos conjuntos se les conoce hoy en día con el nombre de conjuntos Sidon o conjuntos B2. Aunque estos conjuntos aparecen en los números enteros, el concepto es fácil de extender a cualquier grupo abeliano. También es posible considerar sumas de más de dos elementos para obtener los denominados conjuntos Bh (Conjuntos Sidon de orden h).
En 1938, James Singer [13] en su estudio sobre geometría proyectiva finita, demostró el siguiente resultado relacionado con los conjuntos B2.
Teorema 1.1. Si q es una potencia de un primo, entonces existen q +1 enteros α1, a2,...,αq+1 tales que /as q2 + q diferencias αi - αj, distintas de cero representan todos /os residuos no cero módulo q2 + q + 1.
Bose [2] probó un análogo del Teorema de Singer, en 1942.
Teorema 1.2. Si q es una potencia de un primo, entonces existen q enteros α1; α2,..., αq tales que /as q(q - 1) diferencias αi - αj, distintas de cero representan todos aquellos residuos no cero módulo q2 - 1 que no son múltiplos de q + 1.
Como en el anillo de enteros módulo n tener diferencias no cero distintas es equivalente a tener sumas diferentes, los teoremas de Singer y Bose [13, 2] se pueden enunciar en términos de sumas; es decir, se tienen las siguientes consecuencias.
Corolario 1.3. Si q es una potencia de un primo, entonces existen q +1 enteros α1, α2,..., αq+1 tales que todas /as sumas αi + αj, 1 ≤ i ≤ j ≤ q + 1, son distintas módulo q2 + q +1.
Corolario 1.4. Si q es una potencia de un primo, entonces existen q enteros α1; α2,..., αq tales que todas /as sumas αi + αj, 1 ≤ i ≤ j ≤ q, son distintas módulo q2 - 1 .
Más tarde en 1961, Bose y Chowla [3] generalizan los resultados anteriores para sumas de h elementos para todo entero h ≥ 2.
Teorema 1.5. Si q es una potencia de un primo y h ≥ 2 un entero, entonces existen q + 1 enteros α1, α2,..., αq, αq+1 tales que todas /as sumas αj1 + αj2 +・ ・ ・+αjh , con 1 ≤ j1 ≤ j2 ≤ ・ ・ ・ ≤ jh ≤ q+1, son distintas módulo
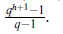
Teorema 1.6. Si q es una potencia de un primo y h > 2 un entero, entonces existen q enteros α1, α2,..., αq tales que todas las sumas
con 1 ≤ j1 ≤ j2 ≤ • • • ≤ jh ≤ q, son distintas módulo qh-1.
El máximo número de elementos de un conjunto Bh contenido en los primeros n enteros positivos se denota mediante Fh(n). De las construcciones mencionadas en los Teoremas 1.5, 1.6 y usando estimaciones de la diferencia entre primos consecutivos se puede deducir que
y además Bose y Chowla conjeturan en [3] que
resultado que se conoce únicamente para h = 2, en [6]. Por otro lado, Jia [10] demostró que
donde o pequeña representa la notación de Landau. Para h = 2r - 1 con r ≥ 1, Chen [5], Bravo, Ruiz y Trujillo [1] y Graham [8] demostraron independientemente que
En este artículo se estudian las construcciones conocidas de conjuntos Bh definidos sobre grupos finitos que provienen de un cuerpo y se obtiene una nueva construcción de un conjunto Bh+s en dimensión h + 1.
2 Conjuntos Bh: conceptos y notación
En lo que sigue del documento G es un grupo abeliano notado aditivamente, A un subconjunto no vacío de G y h ≥ 2 un entero. En esta sección se presenta la definición de conjunto Bh, en un grupo abeliano arbitrario, algunas de sus propiedades y problemas fundamentales.
Definición 2.1 ([14]). Sean (G, +) un grupo abeliano arbitrario, A un subconjunto no vacío de G y h ≤ 2. A se dice un conjunto Bh en G si para todo α1,..., α h, α’1,..., a’h ∈ A se tiene que:
si y solo si (α’1,..., α’h) es una permutación de (α 1, . . . , α h).
Es decir, un conjunto A es Bh en el grupo aditivo G si todas las sumas de h elementos son distintas.
Las siguientes propiedades de conjuntos Bh se deducen directamente de la definición anterior.
Lema 2.2. Si G1, G2 son grupos abelianos y A un conjunto Bh en G1, entonces
A es un conjunto Bt en G1, para todo entero t con 2 ≤ t ≤ h - 1.
Si φ : G1 - G2 es un monomorfismo de grupos, entonces φ (A) = {φ (α) : α ∈ A} es un conjunto Bh en φ (G2).
Definición 2.3. Si A es un subconjunto de un grupo aditivo G y h un entero positivo, entonces la suma iterada hA es:
Si A es un conjunto finito con cardinal |A|, se tiene el siguiente resultado.
Lema 2.4. A es un conjunto Bh si y solo si
Uno de los problemas más importantes sobre los conjuntos Bh consiste en investigar el comportamiento asintótico de las siguientes funciones extremas.
Definición 2.5. Sea fh una función con dominio el conjunto de todos los grupos abelianos finitos y codominio el conjunto de enteros positivos, definida por
para cada G grupo abeliano finito.
En particular si G es cíclico de orden n (G ≅ ℤn) se denota por fh(n) en lugar de fh (ℤn).
Definición 2.6. Sea Fh: ℤ → ℤ+ una función definida por
para cada n ∈ ℤ.
Si A es un conjunto Bh en un grupo finito G, entonces
Esto es,
de donde
En el caso entero, si A ⊂ [1, n] y A es un conjunto Bh en ℤ, entonces aparece un factor h adicional puesto que hA ⊂ [h, hn]:
Para los mejores resultados conocidos sobre estas funciones ver [1, 9, 11].
Si ℤ n se identifica con [1, n] entonces no es difícil ver que todo conjunto Bh en ℤ n se puede considerar como un conjunto Bh entero contenido en [1, n]. Similarmente, si A es un conjunto Bh en ℤ y A ⊂ [ 1, n] entonces A se puede identificar con un conjunto Bh en ℤ hn. Por lo tanto
De las construcciones de Bose y Chowla [3] enunciadas en los Teoremas 1.5 y 1.6 se obtiene como consecuencia las siguientes desigualdades.
Corolario 2.7. Si q es una potencia de un número primo, entonces
3 Construcciones
En esta sección se presenta la construcción de Bose a partir de un cuerpo arbitrario y en particular se presenta la construcción de Singer generalizada.
Teorema 3.1. Si (F, +, •) es un cuerpo, a un e/emento a/gebraico sobre F de grado h ≥ 2 y
la traslación de F mediante a, entonces α + F es un conjunto Bh en el grupo multiplicativo F*(α).
Proof Suponga que existen α i1,..., α ih, aj,..., α jh en F tales que
por factorización única y el hecho de que α es de grado h sobre F, esto es equivalente a que (α + α’ i1 , α + α’ i2, . . . , α + α’ ih es una permutación de (α + α i1, α + α i2 α + α ih).
Ejemplo 3.2.
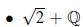 es un conjunto B2 infinito en
es un conjunto B2 infinito en
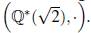
π + ℚ es un conjunto Bh en (ℂ *( π), •), para todo h. En este sentido podría llamarse un conjunto B∞.
Observación 3.3. Si F es un cuerpo finito con q elementos, F = Fq, se tiene el isomorfismo Fqh ≅ (ℤ qh-1, +) mediante la función logaritmo discreto base θ, donde θ es una raíz primitiva de Fqh.
Así:
log θ (α + Fq) es un conjunto Bh en (ℤ qh-1, +).
Si α = θ se tiene la construcción de Bose y Chowla del Teorema 1.6.
Ejemplo 3.4. Sea p = 7, θ un elemento primitivo de F72 con polinomio minimal sobre F7, min F7 (θ) = x2 + 4x + 5 y sea α = θ.
El conjunto
es un conjunto B2 en el grupo multiplicativo F* 49. Usando el logaritmo discreto en la base θ, se tiene que el conjunto
es un conjunto B2 en el grupo aditivo ℤ 48.
Ahora, se presenta la construcción del conjunto Bh tipo Singer generalizada. Aunque en principio la construcción de Singer apareció primero que la de Bose y Chowla, en esta versión se presenta la construcción de Singer como una consecuencia de la construcción de Bose y Chowla tomando como referencia el artículo [7].
Primero se construye un conjunto Bh+1 en el grupo aditivo ℤ qh+1 -1 tipo Bose y Chowla con q elementos, luego este conjunto se reduce módulo (qh + qh-1 +-----+ q + 1), el conjunto resultante es un conjunto Bh en el grupo aditivo ℤ qh+qh-1+ …+q+1 con q elementos, y por último se agrega el cero al último conjunto para así obtener un conjunto Bh tipo Singer generalizado con q +1 elementos en el grupo aditivo ℤ qh+qh-1+…+q+1 .
Teorema 3.5. Si q = pn, con p primo, n ∈ℕ y h ≥ 2 entero, entonces existe un conjunto Bh, con q + 1 elementos, en elgrupo aditivo ℤ qh+qh-1+…+q+1.
Proof Considere el cuerpo Fqh+1 con elemento primitivo θ y α ∈ Fq * h+1 un elemento de grado h+1 sobre Fq. Usando el Teorema 3.1 se construye un conjunto tipo Bose y Chowla a + Fq ⊆ F* qh+1 y por el Lema 2.2 se obtiene el conjunto A = logθ (α + Fq), que es Bh+1 en el grupo aditivo ℤ qh+1-1, con q elementos.
Denote nq: = qh + qh-1 +…+ q + 1.
Ahora, se modula el conjunto A módulo nq, así se obtiene un nuevo conjunto S = A(mod nq). Se va a probar que S es un conjunto Bh en el grupo aditivo ℤ nq.
Suponga que existe un elemento en el grupo (ℤ nq, +) que tiene dos representaciones como suma de h elementos del conjunto S; es decir, existen αi1,..., αih, α’j1..., α’jh en S tales que
esto implica que para algún r ∈ ℤ,
Como para cada elemento α + ui ∈ α + Fq existe un único elemento α i ∈ A tal que logθ (α + ui) = α i, esto implica que
desarrollando los productos, se observa que α satisface un polinomio de grado h en la variable x con coeficientes en F* q,
donde σk = σk(ui1,…, uih), δk = δk(u’i1,…,uih), k = 1,..., h, son las funciones simétricas elementales. Luego como α es de grado h + 1 sobre Fq el polinomio P(x) debe ser el polinomio nulo y así se tiene que
para k = 1 , . . . , h, en consecuencia v = 1 y {ui1, …, uih} = {u’j1,..., ujh }.
Por lo tanto,
Además, S tiene q elementos; en efecto, suponga que existen dos elementos en S que son iguales,
con i # j. Así, existe w ∈ℤ tal que en Fqh+1 se tiene
y como y = θwnq ∈ F*q = (θnq) entonces
Esto implica que
para algún ui, uj ∈ Fq.
Así, α satisface un polinomio de grado 1 con coeficientes en Fq, implicando que y = 1 y ui = uj y así i = j, lo cual es una contradicción. Por lo tanto, todos los elementos de S son distintos.
En consecuencia, S es un conjunto Bh en ℤ nq, con q elementos.
Por otro lado, se tiene que el conjunto S satisface S ∩ (S ⊖ S) = 0, donde S ⊖ S = (S - S) \ {0}. En efecto, suponga que existen s, r, t ∈ S, r # t, tales que s ≡ r - t( mod nq), luego existen a, b, c ∈ Fq y m ∈ ℤ tales que s = logθ(α + α), r = logθ (α + b) y t = logθ (α + c), luego
lo que implica que
tomando w = θ mnq ∈ F* q se tiene que a satisface el polinomio
con coeficientes en Fq, pero como a es de grado mayor o igual que 3 sobre Fq, entonces Q(x) debe ser el polinomio nulo; lo cual no puede ser posible puesto que el coeficiente de x2 es 1, de esto se sigue que S ∩ (S ⊖ S) = 0.
En consecuencia, tomando el conjunto
se obtiene un conjunto Bh en ℤ nq con q + 1 elementos. □
3.1 Nuevas construcciones
Gómez y Trujillo en [7] encuentran una nueva construcción de conjuntos Bh+1, donde realizan el proceso contrario a la construcción de Singer generalizada, ellos a partir de un conjunto Bh obtienen un conjunto Bh+1.
En el Teorema 3.6 se presenta una construcción de un conjunto Bh+s en el grupo producto (Fh, +) x (E*, •), donde E es alguna extensión de F y como consecuencia en el Corolario 3.7 se presenta la generalización a cualquier cuerpo F de la construcción de conjuntos Bh+1 dada por Gómez y Trujillo [7], a partir de un conjunto Bh tipo Bose y Chowla construido en el Teorema 3.1.
Además, es posible obtener otra construcción de un conjunto Bh+1 en dimensión dos en el grupo multiplicativo F * x E * usando la construcción tipo Bose y Chowla de conjuntos Bh, ver Teorema 3.10. Sin embargo en esta construcción se pierde un elemento, por ejemplo para el caso cuando el cuerpo F = Fp, p primo, el conjunto tiene p - 1 elementos.
Sea (Fh, +) el grupo producto de h copias del grupo (F, +). A continuación se presenta la construcción de un conjunto Bh+s en h + 1 dimensiones. Dado el conjunto Ah = {(x,x2,...,xh): x e F}, se conoce por [12] que Ah es un conjunto Bh en el grupo producto (Fh, +), usando la construcción de Bose de un conjunto Bs multiplicativo es posible construir un conjunto Bh+s en h + 1 dimensiones.
Teorema 3.6. Si F es un cuerpo, α un elemento algebraico de grado s ≥ 2 sobre F en alguna extensión E de F y h ≥ 1 un entero. Entonces el conjunto
es un conjunto Bh+s en el grupo producto (Fh, +) x (E *, •).
Proof. Se denota por * la operación dei grupo producto (Fh, +) x (E*, •).
Sean x = {x1,...,xh+s}, y = {y1,...,y h+s} subconjuntos de F tales que
Esto implica que
Las primeras h igualdades, por las identidades de Newton-Girard, implican la igualdad de las funciones simétricas elementales
para 1 ≤ k ≤ h.
Ahora, si se desarrollan los productos de (4) se obtiene
luego usando las igualdades de (5) para 1 ≤ k ≤ h y simplificando se obtiene que α satisface un polinomio de grado s - 1, pero como α es algebraico de grado s sobre F entonces el polinomio debe ser el polinomio nulo, esto implica que
para h + 1 ≤ k ≤ h + s. En consecuencia, {x1,..., xh+s} = {y1,..., yh+s} y por lo tanto
Corolario 3.7. Si (F, +, •) es un cuerpo, a un elemento algebraico de grado h ≥ 2 sobre F en alguna extensión E de F, entonces el conjunto
es un conjunto Bh+1 en (F, +) x (E*, •).
Observación 3.8. En particular si se toma el cuerpo finito F = Fp con p elementos, p primo, entonces E = Fph y (Fp, +) x (Fp, •) es isomorfo a/ grupo (ℤ p x ℤ ph-1, +). Además, como se tiene que mcd(p, ph - 1) = 1 entonces por el isomorfismo del Teorema Chino del Residuo se tiene que ℤ p x ℤ ph-1 = ℤ p(ph-1). Luego usando el Lema 2.2 se obtiene la construcción de Gómez y Trujillo [7] de un conjunto Bh+1 dado por
a partir de un conjunto Bh, donde θ es un elemento primitivo de ℤ p.
Ejemplo 3.9. Del Ejemplo 3.4 se tiene que el conjunto
es un conjunto B2 en el grupo multiplicativo F* 49. Luego el conjunto
es un conjunto B3 en el grupo (F7, +) x (F* 49, •).
Luego usando la construcción de Gómez y Trujillo se obtiene que el conjunto
es un conjunto B3 en el grupo aditivo ℤ 336.
Por otro lado, usando la construcción tipo Bose y Chowla de conjuntos Bh se puede obtener otra construcción de un conjunto Bh+1 en dimensión dos en el grupo multiplicativo F* x E* . Sin embargo, cuando F es un cuerpo finito se pierde un elemento.
Teorema 3.10. Si (F, +, •) es un cuerpo, a un elemento algebraico de grado h ≥ 2 sobre F en alguna extensión E de F, entonces el conjunto
es un conjunto Bh+1 en (F*, •) x (E*, •).
Ahora se presenta la construcción de un conjunto Bh+2 en dimensión tres pegando dos conjuntos conocidos, el conjunto de Sidon
presentado en [4] y el conjunto Bh tipo Bose y Chowla.
Teorema 3.11. Si (F, +, •) es un cuerpo, a un elemento algebraico de grado h ≥2 sobre F en alguna extensión E de F, entonces el conjunto
es un conjunto Bh+2 en (F, +) x (F*, •) x (E*, •).
Observación 3.12. Cuando se tiene e/ cuerpo finito F = Fp, con p elementos y p primo, entonces |A| = p- 1. Luego usando e/ Lema 2.2 se tiene que si A = {(α, α, α + α) : α ∈ Fp *} es un conjunto Bh+2 en (Fp, +) x (F* p, •) x (F* ph, •) entonces el conjunto
es un conjunto Bh+2 en (ℤ p, +) x (ℤ p-1, +) x (ℤ ph-1, +), donde 01 y 02 son elementos primitivos de Fp y Fph, respectivamente.
Además, como mcd(p, ph - 1) = 1 por el isomorfismo del Teorema Chino del Residuo se tiene que el conjunto
es un conjunto Bh+2 en (ℤ p-1 x ℤ p(ph-1), +).
Ejemplo 3.13. Del Ejemplo 3.4 se tiene que
es un conjunto B2 en el grupo multiplicativo F* 49. Además,
es un conjunto B2 en (F7, +) x (F*, •).
Luego
es un conjunto B4 en el grupo (F7, +) x (F* 7, •) x (F49, •).
Ahora, usando el Teorema Chino del Residuo se tiene que
es un conjunto B4 en el grupo aditivo ℤ 6 x ℤ 336.
Por último, como consecuencia del Teorema 3.6 se tiene la construcción de un conjunto Bh+2 en h+1 dimensiones. Como Ah = {(x,x2,...,xh) : x ∈ F} es un conjunto Bh en el grupo producto (Fh, +), usando la construcción de Bose de un conjunto B2 multiplicativo es posible construir un conjunto Bh+2 en h + 1 dimensiones.
Corolario 3.14. Si F es un cuerpo, α un elemento algebraico de grado 2 sobre F en alguna extensión E de F y h ≥ 1 un entero. Entonces el conjunto
es un conjunto Bh+2 en el grupo producto (Fh, +) x (E *, •).
Como los conjuntos Bh con h > 2 no se pueden expresar en forma directa como un equivalente en diferencias, como sí se hace en el caso h = 2, son más difíciles de manipular que los conjuntos de Sidon. Por tal razón, hasta el momento se desconoce el comportamiento asintótico de la función Fh(n) para h ≥ 3, incluso para el caso de la función fh(G) donde G es un grupo abeliano de orden n.
4 Conclusiones
Como consecuencia de las construcciones proporcionadas en los Teoremas 3.6 y 3.11 se tiene que:
Dado el conjunto Ah = {(x,x2,...,xh) : x ∈ F} que es un conjunto Bh en el grupo producto (Fh, +), usando la construcción de Bose de un conjunto Bs multiplicativo es posible construir un conjunto Bh+s en h + 1 dimensiones.
Si F es un cuerpo finito y α es un elemento algebraico de grado h ≥ 2 sobre F en alguna extensión E entonces
Si F es un cuerpo finito y a es un elemento algebraico de grado h ≥ 2 sobre F en alguna extensión E entonces
La construcción del Corolario 3.14 permite obtener familias de conjuntos Bh+2 que son óptimamente densos cuando |G| tiende a infinito; es decir, si A es un conjunto Bh+2 en G = (Fh, +) x (E*, •) se tiene que