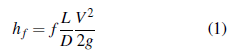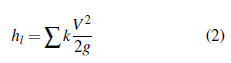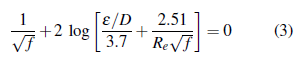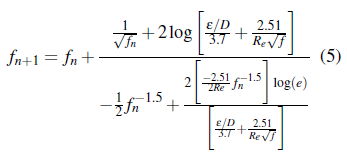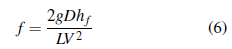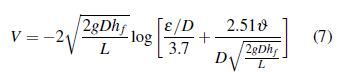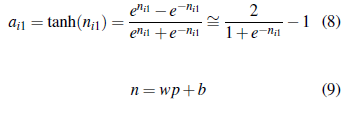1 Introducción
Existen diferentes expresiones para el cálculo del coeficiente de fricción, sin embargo, el modelo propuesto por Colebrook-White ha sido aceptado universalmente estableciendo una función trascendental implícita (3). El diseño hidráulico de tuberías a presión está gobernado por la ecuación de Darcy-Weisbach (1845). Esta expresión establece la pérdida de carga por fricción a partir del coeficiente de fricción (factor adimensional), la longitud de la tubería, el diámetro, la velocidad media del flujo y la aceleración de la gravedad. La ecuación ha demostrado resultados óptimos para flujos completamente desarrollados (flujos turbulentos), condición determinada por el Número de Reynolds (1883). En Colombia los diseños hidráulicos están regulados por el Reglamento Técnico para el Sector de Agua Potable y Saneamiento Básico-RAS-Título B [1].
Donde h f : pérdida de carga (m); f: coeficiente de fricción; L: longitud tubería (m); D: diámetro (m); V: velocidad media del flujo (m/s); g: gravedad (m/s2). Para las pérdidas locales o menores, se tiene:
Donde h l : pérdidas menores (m); k: coeficiente de pérdidas menores (adimensional); V: velocidad media del fluido (m/s); g: aceleración de la gravedad (m/s2). La mayor pérdida que experimentan los sistemas hidráulicos a presión se debe a la resistencia por fricción de la tubería, la cual depende directamente de la rugosidad interior del tubo. De igual forma, las pérdidas de carga por accesorios se producen en las tuberías a presión cuando hay un cambio en el área de la sección transversal del tubo (expansión, contracción) o por el cambio de dirección del flujo, también pueden calcularse en términos de longitudes equivalentes. Así, el comportamiento de la línea de gradiente hidráulico (LGH) varía según el tipo de accesorio. Para una contracción la LGH cae de igual forma que cae la línea de energía (LE). No obstante, para las expansiones bruscas (90°), laLGH aumenta mientras la LE cae súbitamente. Asimismo, el coeficiente de fricción depende de la rugosidad del tubo, del diámetro y del régimen del flujo. La ecuación de Colebrook- White (3) puede ser resuelta a partir del método numérico de Newton-Raphson.
Donde f: coeficiente de fricción (factor adimensional); ε: rugosidad absoluta (m); D: diámetro (m); Re: Número de Reynolds (factor adimensional). La ecuación (3) determina el coeficiente de fricción para flujos completamente desarrollados, es decir para flujos turbulentos con un Número de Reynolds superior a 4000. Si el flujo presenta un comportamiento laminar (Reynolds < 2300), el coeficiente de fricción se obtiene de forma explícita a partir de la ecuación de Hagen-Poiseuille.
El coeficiente de resistencia de Darcy-Weisbach puede ser calculado a través del método numérico de Newton-Raphson, implementado la ecuación de Colebrook-White (3), se tiene:
1.1 Ecuación velocidad del flujo
Aceptando los modelos propuestos por Darcy-Weisbach para el cálculo de las pérdidas generadas por la fricción y Colebrook-White, se tiene:
Despejando el coeficiente de fricción en la ecuación propuesta por Darcy-Weisbach (1) y reemplazándolo en la ecuación de Colebrook-White (3), se obtiene:
dónde f: coeficiente de fricción (factor adimensional); L: longitud de la tubería (m); ε: rugosidad (m); D: diámetro (m); V: velocidad media del flujo (m/s); h f : pérdida de carga por fricción (m); ϑ: viscosidad cinemática (m2/s). La ecuación (7) resuelve la mayoría de problemas hidráulicos propuestos debido a que se establece la velocidad en función de las pérdidas por fricción. Al reemplazar la ecuación (7) en la ecuación de la energía, solamente se tiene como incógnita las pérdidas por fricción, este valor puede ser calculado a partir de métodos numéricos o con la función buscar objetivo de ®Excel. Para garantizar la convergencia del método es importante establecer un valor semilla inicial ajustado a las condiciones de cada problema hidráulico, por lo cual se recomienda que el valor semilla para h f sea el 80% de la pérdida de carga total, esto acelera los tiempos de convergencia.
2 Red neuronal artificial: Especificaciones
2.1 Recopilación y procesamiento de datos
Se implementó el siguiente código en Visual Basic (®Excel). Este código itera de forma automática con una aproximación igual a 1E-012. De esta forma se iteraron 200,000 datos para la rugosidad relativa (ε/D) y el Número de Reynolds (Re) con el objetivo de calcular el valor del coeficiente de fricción (f), el tiempo computacional requerido fue de 12 horas. Esta base de datos está disponible en el siguiente enlace (descarga datos).
Dim i As Integer
Sub Macro_f()
For i = 1 To 50
Range("E5").Select
Do Until ActiveCell = ""
ActiveCell.Offset(0,1).GoalSeek
Goal:=0,ChangingCell:=ActiveCell
ActiveCell.Offset(1,0).Range("A1").Select
Loop
Next i
End Sub
2.2 Escala de los datos
El enfoque de transformación de los datos utilizado en este estudio es el mismo que se utiliza en [2]. De esta forma, el conjunto de datos de entrada se convirtió a una escala logarítmica utilizando el logaritmo en base 10 para el Número de Reynolds (Re) y la rugosidad relativa (ε/D), este procedimiento estableció un rango de [1.61,6.30], esto con el objetivo de limitar la varianza de los datos de entrada [3]. Para el logaritmo de la rugosidad relativa y el coeficiente de fricción se expresó de forma negativa. Estos factores de escala se implementan debido al amplio dominio del Número de Reynolds lo cual afecta el porcentaje máximo de error [4].
2.3 Arquitectura de la red neuronal artificial (RNA)
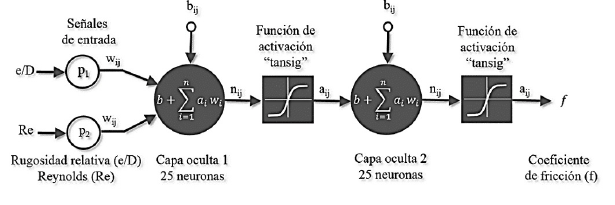
La red neuronal está conformada por entradas (inputs), capas ocultas, pesos sinópticos, funciones de activación, funciones de entrenamiento y salidas (outputs). Esta estructura computacional tiene la capacidad de aprender de los datos para detectar patrones, clasificar y pronosticar escenarios futuros. Para este estudio se estructuró un código utilizando ®Matlab el cual es independiente de las herramientas automáticas del software lo cual permite variar las arquitecturas, las funciones de activación, entrenamiento, y criterios de convergencia. Se implementó el método de Retropropagación de Regularización Bayesiana, el objetivo del modelo es encontrar el mapeo oculto entre las variables de entrada y salida. El número de neuronas ocultas interviene en la eficiencia de aprendizaje y de generalización de la red [5]. Sin embargo, el aumento del número de capas y de neuronas puede originar un sobre ajuste (overfitting) de la red neuronal. Actualmente se desarrollan algoritmos para reducir el sobre ajuste en las redes neuronales. Por ejemplo, el algoritmo (OAA) propone la parada efectiva basada en la estimación de la de relación señal/ruido (SNRF) [6]. Se han propuesto diferentes metodologías para estimar el número de neuronas y capas ocultas [7]. No obstante, la arquitectura óptima se establece a partir del ensayo y el error. Supervisar el seguimiento computacional del proceso que realiza la red neural internamente en la interacción entre las variables de entrada los pesos sinópticos y los sesgos (bias) es complejo. Así, la red neuronal en la fase de explotación constituye una "caja negra" la cual se limita a generar salidas (outputs) a partir de señales de entrada (inputs) [8].
El entrenamiento de la red neuronal constituye un problema de optimización, el cual depende de la escala de las señales de entrada y las funciones de activación. La Tabla 1 presenta los estadísticos para diferentes arquitecturas neuronales. En términos estadísticos y de tiempos computacionales la arquitectura que mostró resultados más favorables corresponde a 2 capas ocultas cada una con 25 neuronas (2-25-25-1). Para este estudio esta arquitectura obtuvo los mejores resultados para los 25,000 datos independientes implementando el método de validación cruzada con un error medio cuadrático igual a 3.60E-05. De igual forma el valor de entropía cruzada para el esquema propuesto fue de 6.60E-03. Sin embargo, para este estudio se realizó la validación a partir del MSE, debido a que la entropía cruzada se aplica usualmente para escenarios de clasificación.
Tabla 1 Arquitecturas realizadas para el cálculo del coeficiente de fricción
| N° capas ocultas | N° de neuronas por capa | Arquitectura | R2 | MAE | MSE | SSE | SAE | BCE |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2-2-1 | 9.99E-01 | 1.00E-03 | 7.65E-06 | 1.53E+00 | 2.93E+00 | 1.54E+00 |
| 1 | 5 | 2-5-1 | 1.00E+00 | 1.32E-04 | 4.61E-08 | 9.00E-03 | 2.63E+01 | 5.84E-01 |
| 2 | 5 | 2-5-5-1 | 1.00E+00 | 2.87E-06 | 2.27E-11 | 4.54E-06 | 5.75E-01 | 1.46E-01 |
| 2 | 25 | 2-25-25-1 | 1.00E+00 | 4.71E-07 | 7.42E-13 | 1.48E-07 | 9.40E-02 | 6.60E-03 |
| 2 | 30 | 2-30-30-1 | 1.00E+00 | 2.79E-06 | 2.44E-11 | 4.88E-06 | 5.58E-01 | 3.00E-03 |
| 3 | 25 | 2-25-25-25-1 | 9.99E+00 | 5.40E-07 | 8.20E-13 | 6.41E-08 | 6.81E-02 | 3.50E-03 |
Fuente: Los autores
La designación del número de capas y el número de neuronas básicamente esta determino por ensayos de prueba y error y de las observaciones de los diferentes criterios estadísticos establecidos. Por lo tanto, estos esquemas deben ser probados bajo diferentes condiciones establecidas por las funciones de entrenamiento y las funciones de activación. El objetivo final del diseño neuronal es minimizar el error cuadrático medio, escapar de mínimos locales y puntos de inflexión generados por la región MSE. Se comprobó que el método de Descenso de Gradiente presentó valores desfavorables probablemente el valor iterado quedo atrapado en mínimo local. Según el modelo propuesto (2-25-25-1) es posible afirmar que existe una relación lineal entre los resultados y los objetivos para este estudio.
3 Metodología
3.1 Entrenamiento de la red neuronal
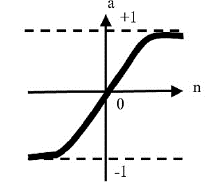
La red se entrenó a partir de 200,000 datos de entrada (inputs) utilizando el algoritmo de Regularización Bayesiana el cual parte de datos iniciales generados de una distribución de probabilidad con el objetivo de generar un conjunto de pesos sinópticos óptimos. Los métodos bayesianos son capaces de resolver de manera consistente y cuantitativa un conjunto de datos ruidosos [9]. Para este estudio se adoptó la función de activación hiperbólica tangente (tansig) para las capas ocultas, según [10] esta función tiene la capacidad de aprender con mayor velocidad y esto se demostró comparado diferentes funciones de activación. La función de activación hiperbólica tangente presenta un mejor rendimiento en arquitecturas neuronales multicapas [11].
El entrenamiento se realiza a partir de valores aleatorios para los pesos sinópticos y los sesgos (bias) de la red. Los pesos se multiplican por cada patrón de entrada y se suma el valor del sesgo, una vez obtenido este valor se activa la neurona a través de la aplicación de la función de activación (tansig) obteniendo una señal primaria de salida. Luego se mide la diferencia entre el patrón de salida real obtenido a partir de la ecuación de Colebrook-White y los valores estimados. Esta diferencia se minimiza implementado el método de Regularización Bayesiana en forma de bucle hacia atrás (retropropagación). La regularización normalmente tiene como objetivo reducir la suma de errores al cuadrado [12].
La función de activación hiperbólica tangente (tansig) está definida por la siguiente expresión,
donde, n está definido como el vector que contiene los pesos sinápticos (w) multiplicados por los patrones (p) de entrada más un valor del sesgo de la red (b); ai1 corresponde a las señales de salida. Usando la regla de Bayes, la probabilidad posterior de los parámetros (w) [9], es,
La Tabla 2 presenta la comparación de diferentes funciones de entrenamiento para la arquitectura (2 25-25-1) utilizando la función de activación (tansig). Aplicando la regla de Bayes para optimizar los parámetros de la función objetivo se obtuvo un MSE igual a 9.45E-09 estableciendo el menor error para las funciones observadas. Se evidencia la dispersión de los valores estimados utilizando el método de Descenso de Gradiente con un MSE de 4.51E-04, esto indica la importancia de evaluar previamente las diferentes funciones de entrenamiento en el proceso de establecer la función óptima para las señales de entrada. En estudios realizados para el cálculo del coeficiente de fricción [2, 8, 13], se implementó la función Levenberg-Marquardt. Sin embargo, no se presenta una comparación con respecto al modelo de Regularización Bayesiana. Este estudio demostró que el método de Regularización Bayesiana es óptimo para reducir la incertidumbre que existe en la predicción del coeficiente de fricción a partir del modelo propuesto por Colebrook-White en términos de esquemas neuronales.
Tabla 2 Comparación funciones de entrenamiento (curva ε /D = 0.000005)
| Funciones de entrenamiento | R2 | MAE | MSE | SSE | SAE | BCE |
|---|---|---|---|---|---|---|
| Bayesian Regularization | 9,98E-01 | 3,14E-05 | 9,45E-09 | 1,89E-05 | 6,20E-02 | 1,58E+00 |
| Levenberg-Marquardt | 9,92E-01 | 3,27E-04 | 8,06E-07 | 1,60E-03 | 6,55E-01 | 5,77E+00 |
| Gradient Descent | 1,77E-01 | 1,61E-02 | 4,51E-04 | 9,03E-01 | 3,22E+01 | 5,76E+00 |
| BFGS Quasi-Newton | 9,72E-01 | 7,40E-04 | 2,55E-06 | 5,10E-03 | 1,48E+00 | 5,76E+00 |
| Gradient Descent with Momentum | 2,49E-01 | 3,10E-02 | 1,00E-03 | 2,24E+00 | 6,14E+01 | 5,76E+00 |
| Scaled Conjugate Gradient | 9,70E-01 | 7,52E-04 | 2.762-06 | 6,00E-03 | 1,51E+00 | 5,76E+00 |
| Variable Learning Rate Gradient Descent | 9,51E-01 | 1,00E-03 | 4,60E-06 | 9,00E-03 | 2,61E+00 | 5,75E+00 |
| One Step Secant | 9,22E-01 | 2,00E-03 | 7,24E+00 | 1,45E-02 | 4,13E+00 | 5,75E+00 |
| Polak-Ribiére Conjugate Gradient | 9,78E-01 | 6,99E-04 | 1,90E-06 | 4,00E-03 | 1,40E+00 | 5,76E+00 |
Fuente: Los autores
La Figura 3 describe la relación entre la curva ε/D = 0.000005 del Diagrama de Moody y el modelo neuronal obtenido (2-25-25-1). Se evidencia que el mejor ajuste se presentó para la función de entrenamiento de Regularización Bayesiana. Como se puede observar en la Tabla 2 los criterios estadísticos para la función de entrenamiento de la Regularización Bayesiana establecen un MSE igual a 9.45E-09. De otro modo, el MSE (1.60E-03) para el modelo Levenberg-Marquardt indican que es inadecuado para este estudio. De igual forma la función de entrenamiento del Descenso de Gradiente presenta gran dispersión de los valores obtenidos por la RNA con respecto a la curva ε /D = 0.000005.
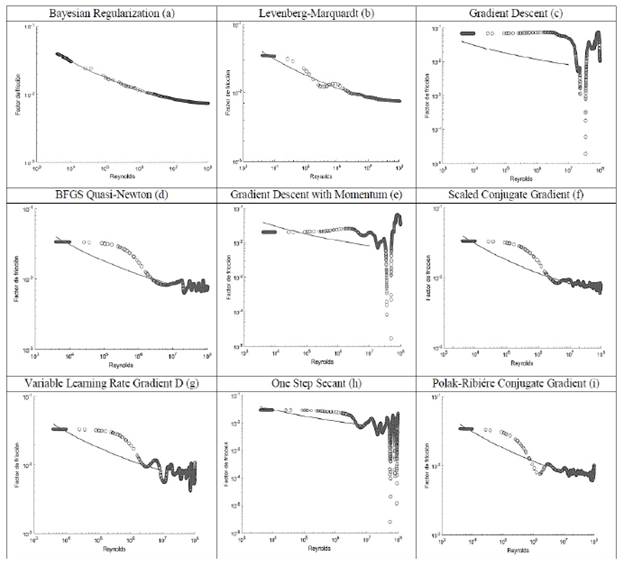
Fuente: Los autores
Figura 3 Funciones de entrenamiento para curva ε/D = 0.000005 (Diagrama de Moody)
La Tabla 2 indica el grado de sensibilidad con respecto a la distribución de los valores estimados. Es decir, es importante verificar gráficamente el comportamiento de los valores estimados a través de la implementación de las diferentes funciones de entrenamiento y compararlos con los valores derivados de la ecuación de Colebrook-White para la curva ε/D = 0.000005. La función de entrenamiento del método del Descenso de Gradiente con Momentum presentó los estadísticos más desfavorables para este estudio (Figura 3e).
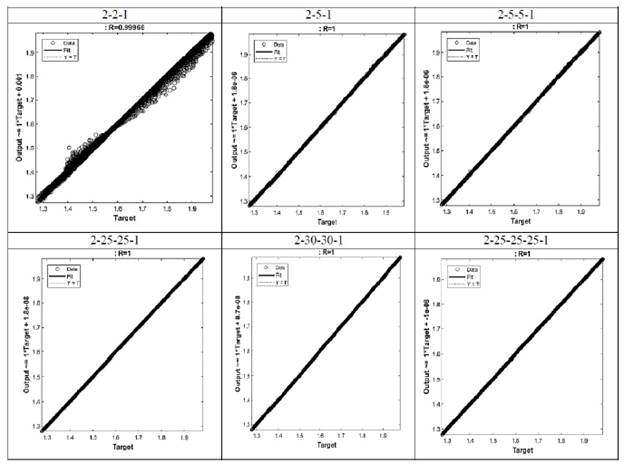
La Figura 4 presenta diferentes arquitecturas asociadas al desempeño del coeficiente de correlación de Pearson (R). La arquitectura (2-25-25-1) presentó el mejor desempeño con el menor costo en tiempo computacional. No obstante, la arquitectura (2-25-25-25-1) presentó valores óptimos para los diferentes criterios estadísticos, pero con un alto costo en tiempo computacional.
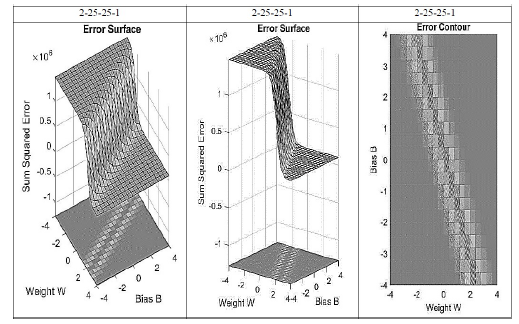
El objetivo final de la función de entrenamiento y la función de activación es minimizar la función de costo, es decir reducir la diferencia entre el valor del coeficiente de fricción establecido por la ecuación de Colebrook-White y los valores estimados por el esquema neuronal. La Figura 5 establece la región formada por la función de costo a partir del MSE para el arreglo (2-25-25-1). Se observa la aproximación al mínimo de la región de errores la cual depende directamente del sesgo y de los pesos sinópticos de la red neuronal.
4 Resultados y discusión
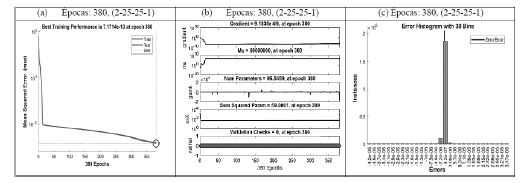
Para este estudio se utilizó la función de entrenamiento trainbr (®Matlab). Esta función actualiza los valores sinópticos de los pesos y de los sesgos minimizando la combinación de errores cuadrados y de pesos. Luego calcula la combinación correcta para producir una red que generalice bien, este proceso constituye la Regularización Bayesiana en ®Matlab. El valor de convergencia se alcanzó para la época 380 con un MSE igual a 7.42E-13 (Figura 6). Las curvas de validación (Figura 6a) presentan un comportamiento similar para este estudio. Dado el caso en el cual la curva de prueba hubiera aumentado con respecto a la curva de validación el modelo estaría sobre ajustado perdiendo la capacidad de generalización.
Tabla 3 Arquitecturas propuestas para el cálculo del coeficiente de fricción
| Autor [Referencia] | Arquitectura | N° Datos | R2 | MAE | MSE | SSE | SAE | BCE |
|---|---|---|---|---|---|---|---|---|
| Ladino, García, García | 2-25-25-1 | 200.000 | 1,00E+00 | 4,71E-07 | 7,42E-13 | 1,48E-07 | 9,40E-02 | 6,65E-03 |
| Brkic and Cojbasic [8, 2] | 2-50-1 | 90.000 | - | 3,66E-07 | 3,34E-09 | - | - | - |
| Offor, Alabi [2] | 2-30-30-1 | 60.000 | 1,00E+00 | 3,89E-07 | 2,46E-15 | 1,48E-10 | - | - |
| Fadare and Ofidhe [13, 2] | 2-20-31-1 | 2.560 | 9,99E-01 | - | 5,34E-07 | 3,41E-04 | - | - |
| Mehran Y., Ayub B. [4] | 2-10-20-1 | 2000 | 9,98E-01 | - | 3,14E-08 | - | - | - |
| Castillo, Solórzano [5] | 2-30-30-1 | 724 | 9,99E-01 | - | 1,75E-04 | - | - | - |
Fuente: Los autores
Tabla 4 Conjunto de datos (Validación cruzada)
| Datos de prueba | Arquitectura | R2 | MAE | MSE | SSE | SAE | BCE |
|---|---|---|---|---|---|---|---|
| 2.000 | 2-25-25-1 | 9,96E-01 | 4,08E-03 | 2.96E+00 | 5.92E-02 | 8.17E+00 | 7.40E-03 |
| 5.000 | 2-25-25-1 | 9,98E-01 | 9,43E-03 | 1.36E-04 | 6.81E-01 | 4.72E+01 | 4.56E-03 |
| 25.000 | 2-25-25-1 | 9,96E-01 | 4,51E-03 | 3.60E-05 | 9.01E-01 | 1.13E+02 | 5.00E-03 |
Fuente: Los autores
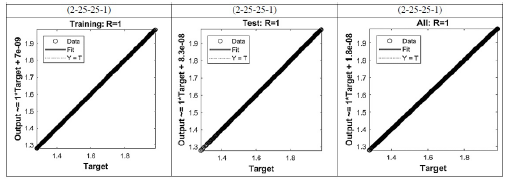
La Figura 7 representa el comportamiento de los datos de entrenamiento, validación y prueba. Para este estudio la línea punteada y la línea continua coinciden en una misma recta lo cual indica que establece un ajuste perfecto con un coeficiente de correlación de Pearson igual a 1, siendo este estadístico la relación entre las variables de entrada y los objetivos. Es posible afirmar que existe una relación lineal entre los resultados y los objetivos.
4.1 Evaluación del rendimiento
El objetivo principal en los procesos de optimización es minimizar el error generado por la función de costo, es decir, localizar el valor que minimiza la función objetivo para el MSE. De hecho, la optimización bayesiana presenta un modelo probabilístico de la función objetivo entrenando la red a partir de la evaluación continua de esta función. Para evaluar la precisión de la arquitectura neuronal propuesta se establecieron 6 criterios estadísticos: R (Coeficiente de correlación de Pearson); MAE (Error absoluto medio); MSE (Error medio cuadrático); SSE (Suma de errores al cuadrado); SAE (Suma absoluta de errores); BCE (Entropía cruzada binaria). La Tabla 3 presenta el comportamiento de los estadísticos del esquema neuronal propuesto con respecto a otros estudios realizados para el cálculo del coeficiente de fricción.
4.2 Validación
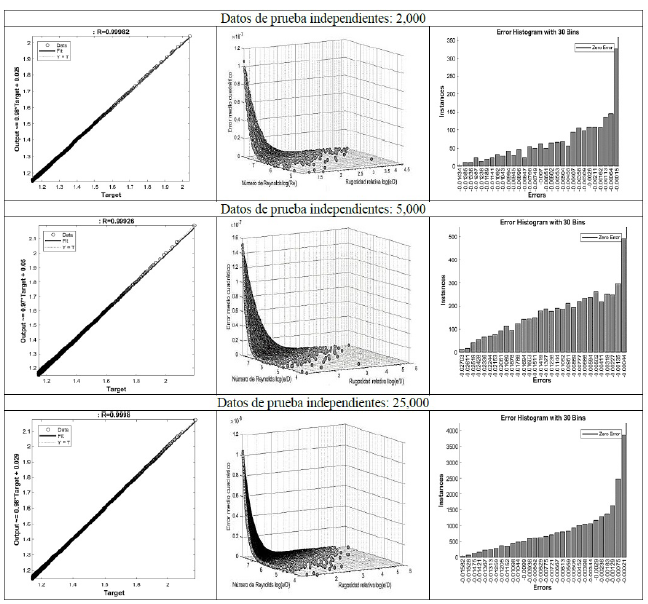
Con el objetivo de garantizar la independencia del subconjunto de datos de entrenamiento y los datos de prueba, se realizó la validación cruzada, este parámetro establece el error de predicción del modelo neuronal. En este sentido, se establecieron tres subconjuntos de 2,000, 5,000 y 25,000 datos para la rugosidad relativa (ε/D) y el Número de Reynolds (Re) independientes de las señales de entrenamiento. La partición entre los datos de entrenamiento y los datos de prueba genera un nuevo valor para el MSE del conjunto de datos independientes. La validación cruzada para el modelo de regresión con los datos predictores (ε/D, Re) y la variable de respuesta (f) estableció que el menor para MSE correspondió al conjunto de 25,000 datos esto se evidencia en la Tabla 4.
Así, en los esquemas neuronales se establecen tres tipos de errores: error irreducible; error por sesgo (bias); error por varianza. El error irreducible o ruido no se puede disminuir y es inherente al comportamiento de las señales de entrada. Por otro lado, un valor bajo en el sesgo (bias) indica menos suposiciones en términos de la función objetivo. Por el contrario, un valor alto del sesgo establece un mayor número de suposiciones de la función objetivo. De igual forma, un valor bajo del error de varianza sugiere pequeños cambios para la función objetivo. Para un valor alto de la varianza se presupone cambios considerables de la función objetivo. En general se debe establecer un balance entre el sesgo y la varianza y esto depende de la escala de los datos, la selección de la arquitectura neuronal, la función de entrenamiento y la función de activación.
4.3 RNA (2-25-25-1): Simulación diagrama de Moody
El Diagrama de Mooody es la representación gráfica a escala logarítmica del coeficiente de fricción a partir de la rugosidad relativa (ε /D) y del Número de Reynolds (Re). A partir de la estructura neuronal propuesta (2-25-25-1) se simuló el diagrama de Moody para 200,000 datos de entrada correspondientes a las señales de entrenamiento. La Figura 9a indica una similitud para las curvas ε/D = 0.05; ε /D = 0.005; ε /D = 0.00005; ε /D = 0.000005. El modelo neuronal comienza a estabilizarse para Reynolds menores a 10E+6. El ruido generado para Reynolds superiores a 10E6 probablemente se deba al escalamiento inicial de los datos, este ruido podría reducirse estableciendo las señales de entrada y de salida en un rango entre -1 y 1.
5 Conclusiones
El valor del coeficiente de fricción de Darcy-Weisbach es fundamental para el cálculo hidráulico de sistemas de tuberías a presión. Este parámetro incide de manera directa en el dimensionamiento y diseño de los diámetros óptimos en el sistema hidráulico. En este sentido, el cálculo no adecuado del coeficiente de fricción puede conllevar a subestimar o sobrestimar los diámetros en los sistemas de tuberías lo cual origina sobre costos en los proyectos de ingeniería. Los resultados obtenidos de la RNA demuestran que la red de retropropagación de Regularización Bayesiana con arquitectura de dos capas ocultas cada una con 25 neuronas (2-25-25-1) tiene la capacidad de calcular el coeficiente de fricción para flujos turbulentos con una aproximación de 10E-7 con respecto a los valores obtenidos implementando la ecuación de Colebrook-White.
La función de activación tansig se ajusta adecuadamente al comportamiento de las señales de entrada determinadas por la rugosidad relativa (ε /D) y el Número de Reynolds (Re). El método de retropropagación de Regularización Bayesiana presentó los mejores resultados para el cálculo del coeficiente de Darcy-Weisbach. Esto se demuestra en la Figura 3, donde se implementaron diferentes funciones de entrenamiento para la ε /D = 0.000005 del Diagrama de Moody. Los resultados obtenidos en la Tabla 4 demuestran que el algoritmo de Regularización Bayesiana presenta mejor rendimiento en términos de costo computacional y del MSE. La Figura 7 establece claramente el ajuste de los datos para la curva ε /D = 0.000005. No obstante, el modelo de entrenamiento de Levenberg-Marquardt presenta un MSE igual a 8.06E-07. De igual forma el método del Descenso de Gradiente evidenció un bajo rendimiento, esto se demuestra en la Figura 3 con un MSE de 4.51E-04.
Finalmente, la Tabla 2 indica el grado de sensibilidad con respecto a la distribución de los valores estimados. Es decir, es importante verificar gráficamente el comportamiento de los valores estimados a través de la implementación de las diferentes funciones de entrenamiento y compararlos con los valores derivados de la ecuación de Colebrook-White para la curva ε /D = 0.000005. La función de entrenamiento del método del Descenso de Gradiente con Momentum presentó los estadísticos más desfavorables para este estudio.