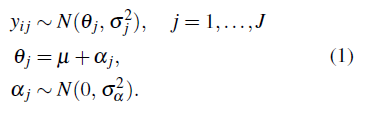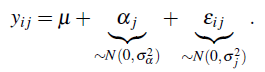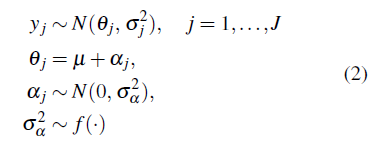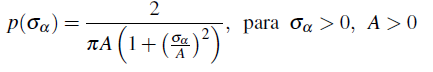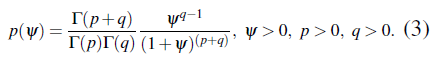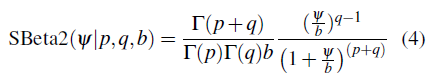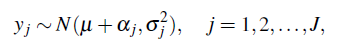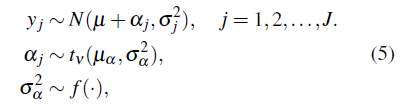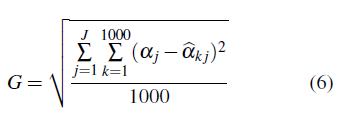1 Introducción

Los modelos jerárquicos se utilizan ampliamente para modelar los datos obtenidos a partir de diseños de medidas repetidas, estudios longitudinales y experimentos aleatorios multinivel diseñados en cuadrado latino, parcelas divididas, bloques balanceados o no balanceados con efectos aleatorios. Para los datos obtenidos de un experimento aleatorio en el que los grupos se ven como una selección aleatoria de una población de grupos, los efectos aleatorios abarcan efectos específicos del grupo, así como entre la variación del grupo [¹]. En el enfoque Bayesiano de modelos jerárquicos, la estructura jerárquica se amplía para incluir otra etapa en la que se dan distribuciones a priori a los componentes de varianza de los efectos aleatorios. Generalmente no hay suficiente conocimiento a priori sobre cuál podría ser la varianza del efecto aleatorio, y por lo tanto se consideran distribuciones a priori no informativas dejando que la verosimilitud domine la inferencia sobre las varianza de los efectos del modelo jerárquico. De las distribuciones a priori para modelar componentes de varianza consideradas en la literatura, la distribución Gamma con parámetros de forma y escala pequeños denotada por Gamma(ε, ε) ha sido comúnmente usada como distribución a priori para la precisión, por lo cual, la distribución Gamma-inversa (ε, ε) se utiliza para modelar el parámetro asociada a varianza. Autores como [³] y [²] exponen e ilustran los principales inconvenientes cuando ε - 0, puesto que se puede dar lugar a distribuciones posteriori propias pero con valores incorrectos o distribuciones posteriori impropias. [⁸] comenta que la Gamma-inversa no es una distribución no informativa y conduce a varianzas muy pequeñas de los efectos y encogimientos fuertes a la media general de los mismos. Por otro lado, [⁴] menciona que típicamente se utiliza una Gamma-inversa con varianza grande para los componentes de varianza. Sin embargo, como su varianza se aproxima a infinito, esta distribución se aproxima a una a priori plana impropia de los componentes de varianza, lo cual conduce a una distribución posterior impropia y tiende a inflar los componentes de varianza para muestras pequeñas.

Hay autores que proponen distribuciones a priori alternativas para modelar el parámetro de escala. [⁴] estudió la distribución a priori encogimiento uniforme para el parámetro de escala en modelos jerárquicos. Muestra cómo la distribución posterior en modelos jerárquicos utilizando esta distribución a priori proporciona una distribución posterior propia. Para modelos jerárquicos [⁸] recomienda inicialmente asignar una distribución a priori Uniforme no informativa para los parámetros de la desviación estándar. Cuando se desea mayor información a priori, por ejemplo, restringir la varianza para que no tome valores grandes, el autor recomienda trabajar con la half-Cauchy(A) como distribución a priori para la desviación estándar, con un valor del paramétro de escala (A) que sea alto. Muestra que esta distribución tiene un mejor comportamiento, compara con la familia Gamma-inversa, cuando la varianza se aproxima a cero.

[⁶] utilizan como distribución a priori una Normal centrada en cero para la raíz cuadrada de cada uno de los parámetros de varianza de un modelo de espacio-estado. Por medio de un estudio de simulación y una aplicación real, muestran que esta distribución es menos influenciable en la inferencia posterior cuando la varianza real del proceso es cercana a cero, comparada con el ajuste cuando se utiliza Gamma-inversa como distribución a priori. Por otro lado, [⁵] presentan la distribución SBeta2 como una familia flexible y manejable para modelar los parámetros de escala. Comentan que esta familia de distribuciones puede obtenerse en forma cerrada como una mezcla de distribuciones Gamma. La familia SBeta2 unifica y generaliza diferentes propuesta de distribuciones a priori para el parámetro de escala y tiene numerosas ventajas teórica y prácticas.

En la mayoría de estudios sobre modelos jerárquicos suponen como distribución para los efectos aleatorios la Normal como elección natural, sin embargo [⁵] comentan que seleccionar la distribución t -Student como a priori para los efectos aleatorio implicaría tener un modelo más robusto. Por lo tanto, el propósito de este estudio es examinar el comportamiento de las estimaciones en un modelo jerárquico para el cual se asumió efectos distribuidos t-Student y diferentes propuestas de distribuciones a priori para el parámetro de escala de los efectos como la Gamma-inversa, half-Cauchy, SBeta2 y Uniforme. Para los grados de libertad de la distribución t-Student se consideraron dos situaciones de interés: la primera asumiendo grados de libertad discretos y la segunda dos alternativas de distribuciones de probabilidad para los grados de libertad.

Este artículo se encuentra organizado de la siguiente manera: la sección 2 se describe el modelo jerárquicos Bayesiano que se analiza en este artículo. En la sección 3 se realiza una revisión sobre las distribuciones a priori del parámetro de escala. En la sección 4 se detalla el estudio de simulación llevado a cabo resaltando los principales aspectos tenidos en cuenta. Finalmente, las secciones 5 y 6 muestran los resultados de los ajustes realizados y una aplicación, respectivamente.

2 Modelos jerárquicos

Los modelos jerárquicos pueden ser usados para una variedad de metas inferenciales incluyendo inferencia causal, predicción y modelado descriptivo. La aplicación de estos modelos se puede dar en áreas tales como: educación, biología, psicología, medicina, entre otras [¹¹, ¹⁰, ¹²]. Los modelos multinivel también se denominan jerárquicos por dos razones diferentes: por la estructura de los datos y por el modelo mismo, que tiene su propia jerarquía. Las dos partes clave de un modelo jerárquico son coeficientes variables y un modelo para esos coeficientes variables (que pueden incluir predictores a nivel de grupo). La característica que distingue los modelos jerárquicos de la regresión clásica está en el modelado de la variación entre grupos [¹³].

2.1 Modelo jerárquico lineal

Los modelos jerárquicos lineales constituyen una clase general de modelos que permiten modelar situaciones en las cuales se tiene datos que presentan una estructura jerárquica. En [⁸, ⁹] presentan un modelo de dos niveles en el cual las observaciones y _ij provienen de una distribución Normal y se presentan efectos a nivel de grupo α_j, en el cual y _ij representa la medición del individuo i en la j-ésima población:

con i = 1,..., n _j las unidades o el número de elementos asociados al j-ésimo grupo, σ _j denota la desviación estándar para las observaciones en el j-ésimo grupo y σ _α denota las desviaciones a nivel de grupo. Así el modelo lineal puede expresarse como sigue:

En el modelo (1) si se supone la varianza dentro de los grupos conocida, entonces podemos modelar de la siguiente manera:

En [¹³, ver sección 19.6] presentan aspectos que se deben tener en cuenta para realizar la elección de la distribución a priori para los parámetros de varianza a nivel de grupo en modelos jerárquicos, en particular discuten el modelo básico de datos de dos niveles y _ij con coeficientes a nivel de grupo α _j del modelo (1). En la siguiente sección se muestran las distribuciones a priori sugeridas en la literatura Bayesiana para el parámetro de escala.

3.1 Distribución a priori half-Cauchy

[⁸] sugirió la half-Cauchy como distribución a priori para la desviación estándar σ_α con parámetro de escala A. El autor recomienda una valor alto de este parámetro cuando se desea mayor información a priori, por ejemplo restringir la varianza para que no tome valores grandes. La función de densidad de probabilidad es:

Esta distribución tiene un mejor comportamiento, comparada con la familia Gamma-inversa, cuando la varianza se aproxima a cero.

3.2 Distribución Beta 2 Escalada (SBeta2)

[²⁰] propone la distribución SBeta2 como distribución a priori para los parámetros de escala. Esta distribución es una versión escalada de la distribución Beta2, también conocida como distribución beta inversa o distribución beta prime la cual es una forma estándar de la distribución de Pearson tipo VI. La distribución Beta2 para ψ está definida como:

La distribución SBeta2 para ψ se define como:

En una distribución SBeta2( p, q, b) el parámetro p controla el comportamiento en el origen, el parámetro q rige el comportamiento en la cola derecha de la distribución de tal manera que mientras más pequeño sea más pesada es la cola y b > 0 controla la escala de la distribución.

4 Estudio de simulación

4.1 Diseño del estudio de simulación

Para el estudio de simulación se generan datos de acuerdo al modelo

donde j corresponde al número de grupos, μ ∼ N(0,1 + 06), el parámetro de varianza σ_j ² se asume conocido y aj denota el efecto aleatorio en el j-ésimo grupo. Los valores de los σ_j ² se tomaron iguales a los trabajados en [²⁰][ver sección 4.1]. Los valores de los efectos aleatorios aj se consideraron fijos de acuerdo a los siguientes escenarios:

• (a) Escenario 1: todos los efectos con una magnitud similar. En este escenario, los valores de los α _j se consideran fijos en el siguiente intervalo [-0.5,0.5].

• (b) Escenario 2: algunos valores atípicos moderados. En este escenario, los valores de los α _j se establecen en tres intervalos de valores diferentes entre los cuales encontramos: (-0.5,0.5), (-2,2) y (-3,3). El número de valores atípicos asignados por grupos varía. Para J = 3, 4, 5 grupos, se asigna un solo valor atípico moderado. Cuando J = 6,7 se asignan dos valores atípicos moderados y para J ≥ 8 se asignan tres valores atípicos moderados.

• (c) Escenario 3: un efecto con un gran valor atípico. En este escenario, se considera solo un efecto tal que su valor absoluto supere 5 unidades, el resto de los valores de los α _j se establecen en un intervalo de valores (-0.5, 0.5).

Los valores de los efectos aj por cada escenario de interés corresponden a los trabajados en [⁵]. Se simulan datos para J = 3,4,5,6,7,8,9,10. Para cada valor fijo de α _j , σ_j ² y J se generan 1000 muestras de una distribución Normal por cada uno de los escenarios en consideración. Con estas muestras se realizó el siguiente ajuste:

con µ_a - N (0,1 + 06) y f (●) denota la distribución a priori para el parámetro de escala σ _α ² . Las distribuciones a priori candidatas utilizadas para modelar el parámetro de escala σ _α ² se asocian a las diferentes propuestas realizadas por [²], [⁸] y [⁵] las cuales están mencionadas en la sección 3 y corresponden a las distribuciones Gamma-inversa (ε, ε) con ε = 0.001, Uniforme(0,1/ ε) con ε = 0. 01. De acuerdo a [²⁰] para una inferencia robusta cuando se utiliza como distribución a priori para los parámetros de escala la distribución SBeta2, se sugiere seleccionar q entre 0 y 1 y p entre 0.5 y 1, por lo tanto se seleccionan como valores de estos hiperparámetros p = q = 0. 5 y p = q = 1. Por otro lado, [⁸] estudia el modelo jerárquico Normal y propone utilizar como distribución a priori para σ _α la half-Cauchy(25), lo que corresponde a modelar σ _α ² con una distribución SBeta2(0.5,0.5,625), entonces se selecciona como valor de b = 625. Adicionalmente, siguiendo a [⁵], también se estudian los valores del hiperparámetro b de tal manera que se cumpla el enunciado de probabilidad p( σ _α ² > Varianza(α_j) = 0.5 pues cuando p = q la mediana de la distribución SBeta2 es el parámetro de escala b, entonces b = Varianza(α_j).

Con respecto a los grados de libertad de la distribución t-Student se trataron bajo dos escenarios, inicialmente se consideran grados de libertad discretos v = 1,2,3,4,5,10,30 utilizados en [⁹] y un segundo escenario fue considerarlos como un parámetro desconocido y utilizar las distribuciones a priori propuestas por [¹⁵] y [¹⁴], en las cuales proponen modelar los grados de libertad v en una distribución t -Student a partir de una distribución Gamma tal que v ∼ Gamma(2, 0.1) y de una distribución Exponencial siendo v ∼exp(0.001). Por cada escenario de interés se obtiene como resultado por cada número de grupo J en consideración 10000 simulaciones de las cadenas a posteriori de los parámetros del modelo jerárquico lineal a partir del método MCMC, utilizando el software jags [¹⁸] y la librería R2jags [¹⁹] del software estadístico R [¹⁷], estableciendo un quemado inicial de 2000. Para estudiar el efecto de las diferentes distribuciones a priori candidatas para el parámetro de escala σ _α ² , se utilizó como medida el error global de estimación, el cual está dado por la siguiente expresión:

donde α^ _kj denota la mediana de la distribución posterior de αj para la k-ésima muestra.

5 Resultados obtenidos del estudio de simulación

Por cada escenario de interés se presenta el comportamiento de la medida de error global de estimación, G, asociado a los efectos aleatorios estimados. Adicionalmente se compararon los valores de G obtenidos con los presentados en [⁵], donde se modelan los efectos aleatorios utilizando como distribución a priori la Normal.

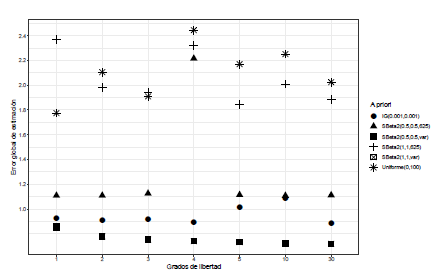
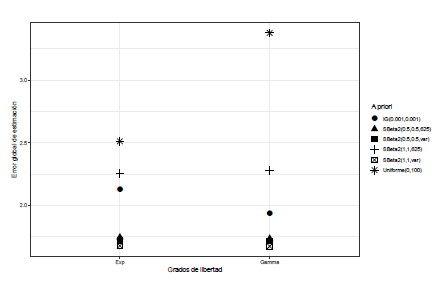
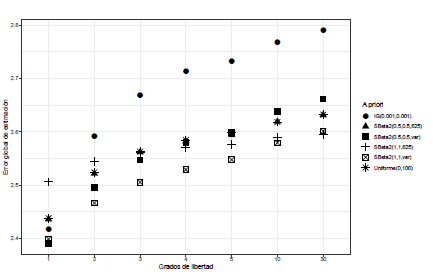
Para el escenario 1, todos los efectos con una magnitud similar, se puede observar en las Figuras 1 y 2 el comportamiento de G cuando se utilizan grados de libertad discretos en la distribución t-Student para modelar los efectos aleatorios, para cada una de las distribuciones a priori ajustadas para el hiperparámetro σ_α ². En la Figura 1, cuando J = 3, se puede observar que el comportamiento de los valores de G se pueden clasificar en valores altos y bajos, siendo los valores más altos cuando se utiliza como distribución a priori para σ_α ² la SBeta2(1,1,625) y Uniforme(0,100), seguido de la distribución SBeta2(0.5,0.5,625). Esto se da para todos los grados de libertad.

Figura 1 Error global de estimación para J = 3 en el escenario 1. 

Figura 2 Error global de estimación para J = 6 en el escenario 1. 

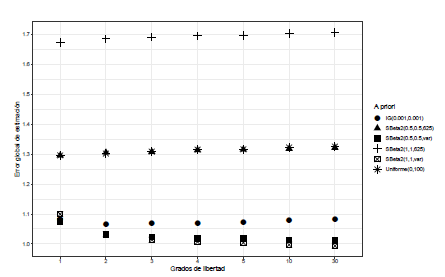
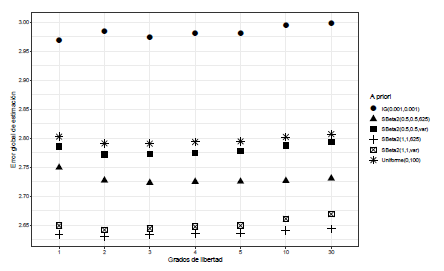
Por otro lado para J = 6, nuevamente en el escenario 1, en la Figura 2 se puede ver que el error cuadrático medio se puede clasificar en tres grupos: valores altos de G, valores promedios y valores de G bajos. En el primer grupo encontramos la distribución a priori SBeta2(1,1,625), el segundo grupo se da cuando la distribución a priori es la SBeta2(0.5,0.5,625) y Uniforme(0,100). Para el último grupo, valores bajos del error cuadrático medio, se dan con las distribuciones a priori son: SBeta2(1,1,Varianza(αj)), SBeta2(0.5,0.5, Varianza(α _j )) y Gamma-inversa(0.001,0.001).

En general para el escenario 1, para todos los valores J y en todos los grados de libertad discretos de la distribución t-Student, los mayores valores del error cuadrático medio se dieron cuando la distribución a priori para σ_α ² es SBeta2(1,1,625) y SBeta2(0.5,0.5,625), lo cual es razonable dado que se está asignando una distribución a priori con un parámetro de escala muy grande (b = 625) en un escenario donde los efectos son muy similares en magnitud y por lo tanto su varianza es pequeña.

Nuevamente en el escenario 1, cuando los grados de libertad de la t-Student son continuos, para todo J, se observa el mismo comportamiento; mayores valores de G cuando la distribución a priori es SBeta2 con b = 625 y Uniforme(0,100). En este escenario 1 la distribución a priori Gamma-inversa(0.001,0.001) presenta valores bajos del error cuadrático medio, tanto para los grados de libertad discretos como continuos de la t-Student.

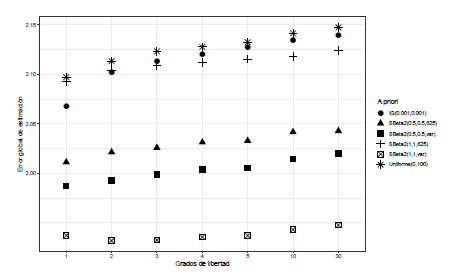
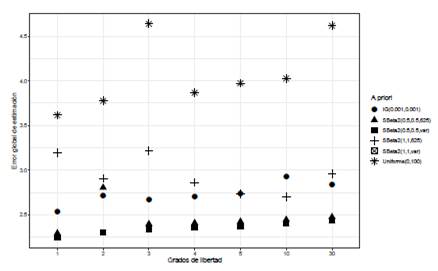
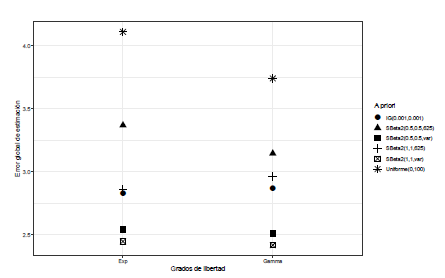
En el escenario 2, algunos valores atípicos moderados, los resultados del estudio de simulación se van a comentar de acuerdo al número de valores atípicos en los grupos. Para J =3, 4 y 5, donde se tiene un solo valor atípico moderado, se encuentra que el error cuadrático medio es mayor cuando se utiliza como distribución a priori para σ_α ² la SBeta2(1,1,625), Uniforme(0,100) y Gammainversa(0.001,0.001). Por ejemplo, en la Figura 3 se puede ver el comportamiento de G, cuando J = 5 y los grados de libertad de la t-Student son discretos, se observa que cuando se utiliza la distribución Uniforme(0,100) se presenta un mayor error global de estimación, seguido de la SBeta2(1,1,625) o la Gamma-inversa(0.001,0.001). También se observa que la tendencia de los valores G es creciente a medida que aumentan los grados de libertad de la distribución t-Student. Por otro lado, cuando se utilizan grados de libertad continuos, se puede ver en la Figura 4 que la distribución que presenta mayores valores de G es la Uniforme(0,100), seguido de las distribuciones SBeta2(1,1,625) y Gammainversa(0.001,0.001). Esto sucede para J = 3,4,5 y coincide con el comportamiento de G cuando los grados de libertad son discretos.

Figura 3 Error global de estimación para J = 5 en el escenario 2. 

Figura 4 Error global de estimación para J = 5 en el escenario 2. 

Cuando J = 6, 7 y se tienen dos valores atípicos moderados en los efectos, el mayor error cuadrático medio se tiene cuando la distribución a priori para σ_α ² es Gamma-inversa(0.001,0.001), ver Figura 5. Esto también sucede cuando se modelan los grados de libertad continuos, el mayor error global de estimación se da cuando la distribución a priori para σ_α ² es Gamma-inversa(0.001,0.001).

Figura 5 Error global de estimación para J = 5 en el escenario 2. 

Para J = 8,9,10, escenario 2, donde se tienen tres valores atípicos moderados, tanto para grados de libertad discretos como continuos, los mayores valores de G se obtienen cuando la distribución a priori es SBeta2(0.5,0.5,Varianza( α_j)) y Gamma- inversa(0.001,0.001).

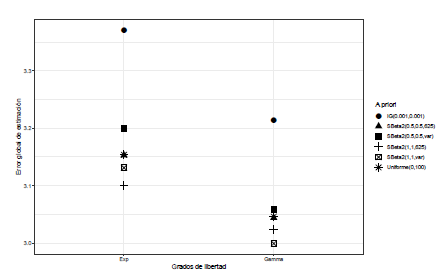
La Figura 6 ilustra el comportamiento de G para el tercer escenario, un efecto con un gran valor atípico, con j = 3 y grados de libertad discretos. Se evidencia que los valores más altos se presentan con el ajuste σ _α ² ∼ Uniforme(0,100), los menores valores se presentan con los ajustes SBeta2(1/2,1/2,625), SBeta2(1,1,Varianza(α_j)) y SBeta2(1/2,1/2,Varianza(α_j).

Figura 6 Error global de estimación para J = 3 en el escenario 3. 

En el caso de J = 3 grupos y grados de libertad continuos para la distribución t de Student a partir de la propuesta de [¹⁵], el ajuste σ _α ² ∼ Uniforme( 0, 100) presentan los mayores de G con respecto a las otras distribuciones a priori y se puede evidenciar en la Figura 7.

Figura 7  Error global de estimación para J = 3 en el escenario 3 con grados de libertad continuos. 

Para J ≥ 4, tanto grados de libertad discretos como continuos, los mayores valores de G se dan cuando σ _α ² ∼Gamma-inversa(0.001,0.001), ver Figuras 8 y 9.

Figura 8 Error global de estimación para J = 5 en el escenario 3 con grados de libertad discretos. 

Figura 9 Error global de estimación para J = 8 en el escenario 3 con grados de libertad continuos. 

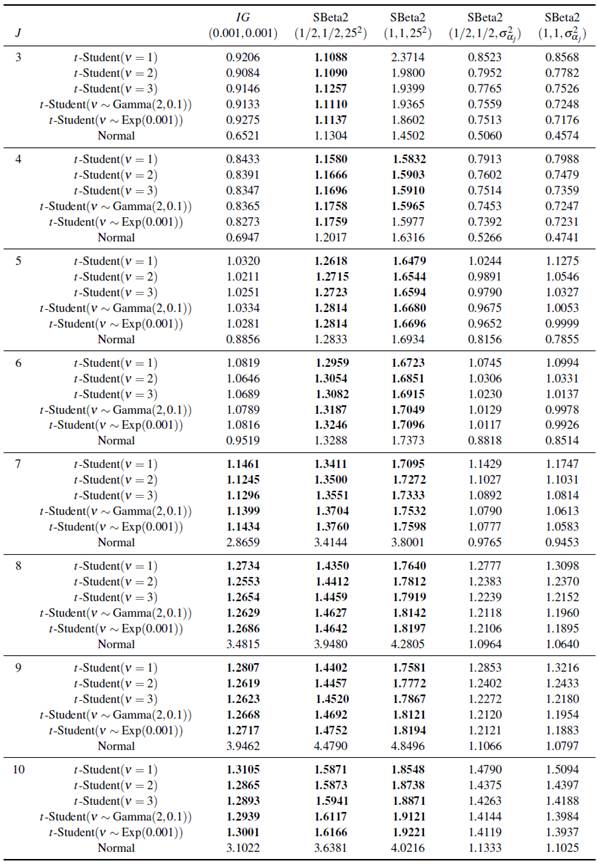
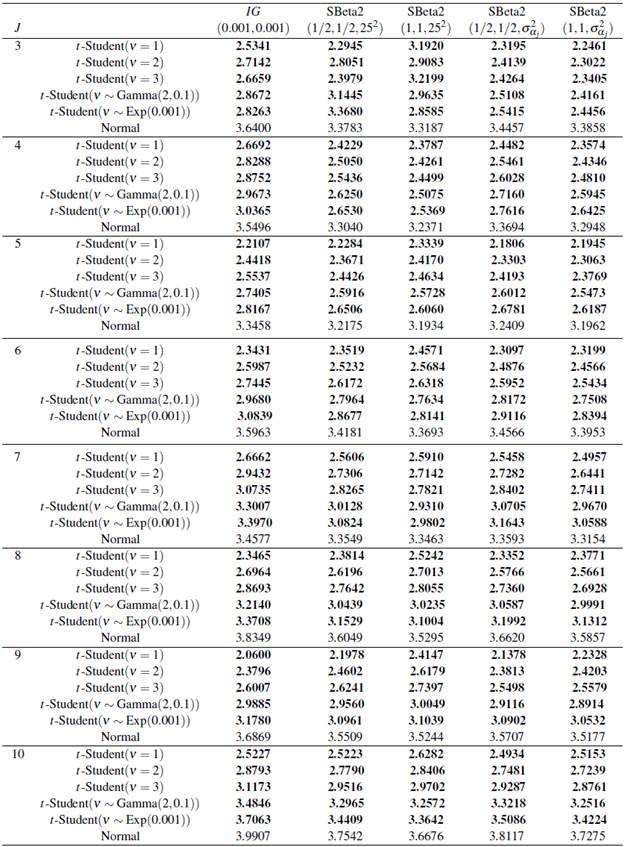
Para evaluar el comportamiento conjunto de modelar los efectos los efectos aleatorios con una distribución t de Student teniendo diferentes distribuciones a priori para el parámetro de escala, se comparan los resultados del error de la estimación de los efectos del modelo obtenidos vía simulación con los reportados en [⁵], donde los efectos aleatorios fueron modelados mediante una distribución Normal. Se realiza la comparación para v = 1, 2 y 3, valores que hace que la distribución t de Student tenga colas más pesadas, y los grados continuos. Algunos de los valores G de interés para realizar la comparación se presentan en la Tabla 1. Se observa, para el escenario 1, cuando J= 3, los menores valores de G se dan cuando se modelan los efectos aleatorias mediante una Normal, excepto cuando la distribución a priori para σ _α ² es SBeta2(0.5,0.5,625). Cuando J=4,5 y 6, los menores valores de G se dan cuando se ajusta σ _α ² con las distribuciones SBeta2(0.5,0.5,625) y SBeta2(1,1,625) y los efectos aleatorios son modelos con una distribución t de Student. En el caso de J = 7, 8, 9, 10 se obtienen valores de G menores a los reportados bajo el ajuste de los efectos con una distribución Normal cuando la distribución a priori de σ _α ² es Gamma-inversa(0.001,0.001), SBeta2(0.5,0.5.625) y SBeta2(1,1.625).

Tabla 1 Comparación de errores de estimación global, G, para el escenario 1. 

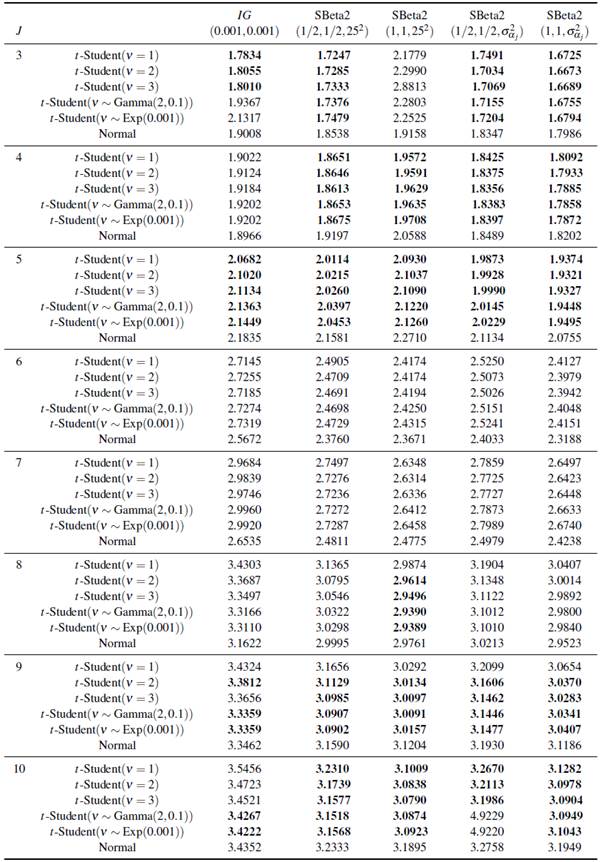
Los resultados de la comparación del escenario 2 con el estudio [⁵] se observan en la Tabla 2. Para J = 3, 4 en los cuales hay un solo valor atípico moderado, los mayores valores G se dan cuando la distribución a priori para los efectos aleatorios siguen una distribución Normal, excepto cuando se realiza el ajuste σ _α ² ∼SBeta2(1,1,625) y cuando σ _α ² ∼Gamma-inversa(0.001,0.001) con grados de libertad continuos para la distribución t-Student. Cuando J = 5 todos los valores G son menores comparados con los reportados por [⁵]. Para J ≥ 6 y 7 el ajuste de los efectos aleatorios con una distribución Normal presenta menores valores G.

Tabla 2 Comparación de errores de estimación global para el escenario 2. 

Para el escenario 3, un gran valor atípico, los resultados de la comparación se aprecian en la Tabla 3. Se observa que para todos los grupos los valores G son menores cuando los efectos aleatorios siguen una distribución t-Student. La distribución a priori para σ _α ² con los valores más altos es Gamma-inversa(0.001,0.001). Así, podemos establecer que bajo las condiciones del escenario 3 se presentan los menores valores de G, los cuales incrementan a medida que aumenta el valor de los grados de libertad, en cambio que, en los escenarios 1 y 2 se presentan valores más altos para G y una tendencia a disminuir a medida que aumentaban los grados de libertad.

Tabla 3 Comparación de errores de estimación global, G en el escenario 3. 

6 Aplicación de un modelo jerárquico Normal

Consideramos el modelo jerárquico lineal dado en (2) el cual se aplicó a los datos del ejemplo de los colegios analizado en [⁸] en el nivel 1 y distribuciones a priori para σ _α ² en el nivel 2 las listadas en la sección 2.2. Los datos corresponden al efecto relativo de un programa de entrenamiento sobre una prueba de actitud escolar en ocho colegios, en el modelo los parámetros α _j para j = 1, 2,..., 8 representan el efecto relativo del programa de entrenamiento en el j-ésimo colegio y σ _α la desviación estándar de dichos efectos entre los colegios. Los efectos son medidos como puntaje en la prueba y están entre 200 y 800 con un promedio aproximado de 500, por lo cual, el mayor efecto está alrededor de los 300 puntos y para la desviación estándar entre estos efectos, σ _α se define como límite superior de 100.

De la Figura 10 a la Figura 13 se presentan los histogramas de frecuencias para la distribución posterior del parámetro σ _α ajustado por cuatro diferentes alternativas para la distribuciones a priori a partir de métodos Monte Carlo por cadenas de Markov basado en 10000 simulaciones del modelo ajustado en jags bajo el paquete R2jags con un quemado inicial de 2000 iteraciones.

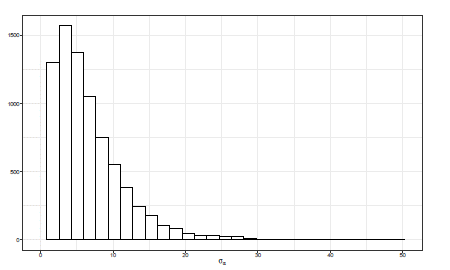
Figura 10 Histograma de la distribución posterior de σ _α con distribución a priori para σ _α ² ∼SBeta2(1/2,1/2,25²). 

En la Figura 10 se presenta el comportamiento cuando se utiliza como distribución a priori para σ _α ² una SBeta2(1/2,1/2,25²), la cual es equivalente a realizar el ajuste con una haJf-Cauchy(25) para σ _α Se evidencia que a partir de valores de σ _α superiores a 15, se empieza a extender una pequeña cola, por lo cual, los valores para σ _α son admisibles en términos de la cota superior, esto es, σ _α < 100.

En el caso del ajuste σ _α ² ∼SBeta2(1,1,25²) presentado en la Figura 11 una pequeña cola a derecha se empieza a extender a partir de valores de σ _α mayores de 20 considerados como admisibles y, comparando con los resultados del ajuste con σ _α ² ∼ SBeta2( 1/2,1/2,25²), se presenta una media con mayor cuantía.

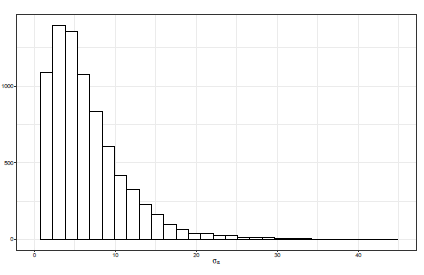
Figura 11 Histograma de la distribución posterior de σ _α con distribución a priori para σ _α ² ∼SBeta2(1,1,25²). 

El ajuste con una distribución a priori Uniforme presentado en la Figura 12, la cual [⁸] recomienda para J ≥ 5 grupos, tenemos que la cola a derecha se empieza a extender a partir de valores de σ _α superiores a cuatro y se presenta una gran concentración en el intervalo (0,4) pero no con picos altos alrededor de cero, es decir, esta distribución a priori captura desviaciones pequeñas para los J = 8 grupos que se están comparando con valores de σ _α en un rango admisible.

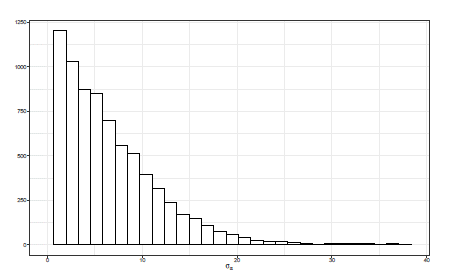
Figura 12 Histograma de la distribución posterior de σ _α con distribución a priori para σ _α ² ∼Uniforme(0,100). 

En contraposición a lo presentado con el ajuste σ _α ² ∼ Uniforme(0,100) tenemos el comportamiento del ajuste σ _α ² ∼ Gamma-inversa(0.001,0.001), el cual se puede apreciar en la Figura 13, donde el rango de valores se encuentra concentrado en un intervalo pequeño, con un pico muy alto alrededor de cero y una pequeña cola a derecha extendiéndose a partir de valores de o superiores a 5, por lo tanto podemos establecer que la inferencia se va a ver afectada debido al encogimiento de los efectos en cada grupo, α _j .

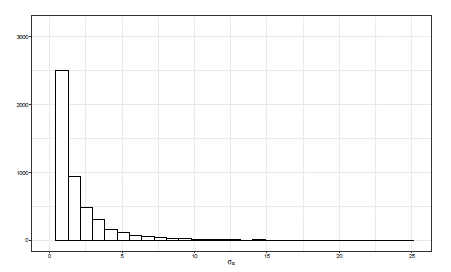
Figura 13 Histograma de la distribución posterior de σ _α con distribución a priori para σ _α ² ∼IG(0.001,0.001). 

Por tanto, podemos establecer con el análisis gráfico de las distribuciones posteriori que, se obtienen valores de σ _α admisibles, menores que los reportados en [⁸], [⁹] y [⁵] ajustando los efectos aleatorios a una distribución t-Student.

7 Conclusiones

En el presente trabajo se propone e implementa al análisis conjunto de modelar los efectos aleatorios de una modelo jerárquico Normal a partir de una distribución t-Student, desde un enfoque Bayesiano, utilizando diferentes distribuciones a priori para el parámetro de escala. A partir de un estudio de simulación, se analizó el comportamiento de las estimaciones de los efectos aleatorios del modelo jerárquico, teniendo como medida de desempeño el error global de estimación. Se utilizaron diversas propuestas para el parámetro grados de libertad de la distribución t-Student.

A partir de los resultados obtenidos del estudio de simulación se evidencia la tendencia de incremento del error global de estimación a medida que aumentan los grados de libertad asociados a la distribución t-Student, para todos las distribuciones a priori para el parámetro de escala que fueron analizadas.

De acuerdo con lo escenarios analizados se observó en el escenario 1 que los menores valores del error global de estimación se obtienen cuando se realizan los ajustes de σ _α ² con las distribuciones SBeta2(0.5,0.5,Varianza(α_j)) y SBeta2(1,1,Varianza( α_j)). En los escenario 2 y 3, valores atípicos moderados y un gran valor atípico, respectivamente, los valores más altos del error global de estimación se dieron cuando la distribución a priori para σ _α ² es Gamma-inversa(0.001,0.001), en la mayoría de los casos.

Los resultados de la comparación del escenario 3,un gran valor atípico, con el estudio [⁵] muestran que para todos los grupos los valores G son menores cuando los efectos aleatorios siguen una distribución t-Student. La distribución a priori para σ _α con los valores más altos es Gamma-inversa(0.001,0.001). Así, podemos establecer que bajo las condiciones de este escenario se presentan los menores valores de G, los cuales incrementan a medida que aumenta el valor de los grados de libertad, en cambio que, en los escenarios 1 y 2 se presentan valores más altos para G y una tendencia a disminuir a medida que aumentaban los grados de libertad.