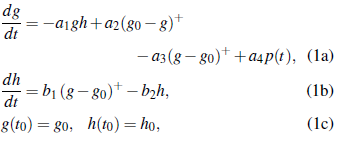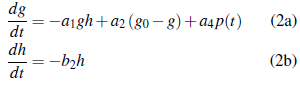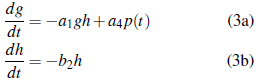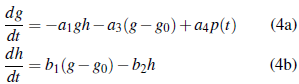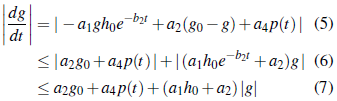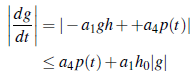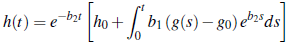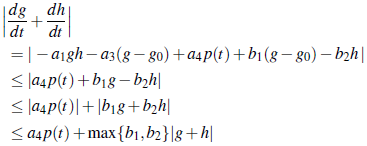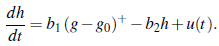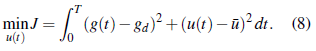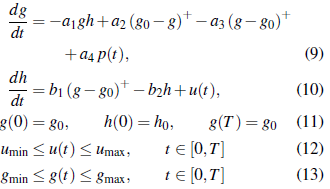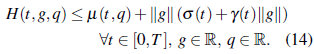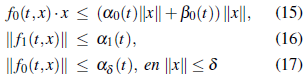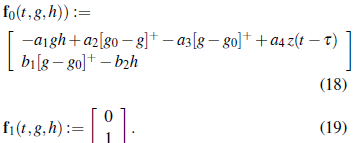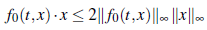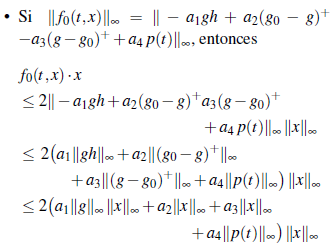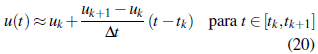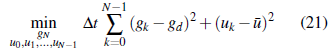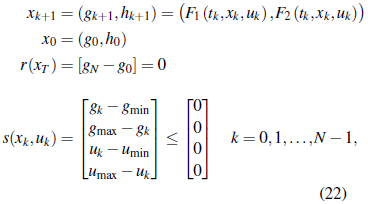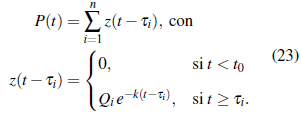1 Introducción

La diabetes es una patología que se caracteriza por una elevada cantidad de glucosa que permanece circulando por el torrente sanguíneo, debido a que el páncreas deja de producir insulina o produce muy poca cantidad. El principal tratamiento de esta enfermedad consiste en la administración de insulina fabricada artificialmente en laboratorios farmacéuticos, intentando así imitar el funcionamiento del páncreas. Actualmente, la inyección de insulina en pacientes diabéticos puede hacerse a través de bombas de infusión continua, pero estas bombas aún dependen de la manipulación del paciente, que sigue siendo sobre quien recae la responsabilidad de realizar los cálculos de la cantidad de insulina a suministrar y aceptar o corregir las sugerencias hechas por el dispositivo. Errores en estos cálculos pueden ocasionar problemas de salud que afectan considerablemente la calidad de vida del paciente, por lo que se busca dotar a estos dispositivos de un algoritmo capaz de estimar la cantidad de insulina necesaria en cada momento para mantener la concentración de glucosa dentro de un rango objetivo, usando la menor cantidad de medicamento que sea posible. Esto se conoce en matemáticas como un problema de control óptimo, y en este trabajo se presenta una alternativa de solución a este problema. Automatizar y mejorar el manejo de la diabetes es el principal objetivo de desarrollar lo que se denominaría un páncreas artificial.

Desde el punto de vista matemático se han propuesto y analizado diversos modelos matemáticos para entender la regulación normal o anormal de la glucosa. El primer modelo relevante que describe la interacción entre glucosa e insulina, fue introducido por [¹⁰] y estudiado en [¹]. En estos trabajos se propone un sistema de ecuaciones diferenciales lineales, que interpreta la dinámica glucosa insulina como un oscilador armónico amortiguardo, se emplean varias mediciones de glucosa en perros [¹⁰] y resultados de la prueba oral de glucosa en humanos [¹] para estimar los parámetros del modelo. En particular, basados en el tipo de oscilación amortiguada en [¹] se propone un criterio para distinguir entre individuos sanos, prediabéticos y diabéticos leves. Posteriormente, este modelo pionero ha sido extendido a modelos lineales y no lineales. Por ejemplo en [⁹] se introduce el efecto de insulina activa, que está relacionada con la concentración de insulina en sangre en la medida en que su actuación afecta la captación de glucosa por parte de los tejidos, así como la absorción y producción por parte del hígado. Este modelo es conocido con el nombre de modelo minimal de Bergman y es ampliamente usado para determinar los indices de sensibilidad de la glucosa y efectividad de la glucosa mediante prueba de tolerancia intravenosa a la glucosa. Más recientemente en [¹⁵] se propone un modelo de ecuaciones diferenciales que incorpora regímenes de una sola dosis o dosis periódicas de insulina para pacientes diabéticos. Un modelo mas complejo es introducido en [¹⁸] este consta de un sistema de ecuaciones diferenciales que describen las reacciones de 45 metabolitos involucrados en el metabolismo de la glucosa hepática en humanos. El modelo reproduce la dependencia observada experimentalmente del metabolismo de la glucosa de las hormonas, como la insulina, glucagón y epinefrina entre otras. Una excelente reseña de estos y otros modelos matemáticos; y su impacto en el estudio de la regulación de la glucosa en la sangre se puede encontrar en [²] y [²⁷].

Por otra parte, es de recalcar que uno de los objetivos principales de los modelos propuestos desde [¹] es determinar criterios para facilitar el diagnóstico temprano de la diabetes a partir de pruebas de laboratorio como la prueba oral de tolerancia a la glucosa (OGTT); aunque, dado el número de parámetros de los modelos [¹], [⁹] y [¹⁸] esto no ha sido una tarea fácil. Es así, que muy recientemente en [³⁰] se propone un modelo de una sola ecuación diferencial con retraso de primer orden que elimina la interferencia del sistema nervioso que percibe el hambre y la saciedad, mejorando así, la extracción de información a partir de la prueba (OGTT). El análisis estadístico muestra la superioridad del criterio de diagnóstico propuesto sobre el recomendado por la Organización Mundial de la Salud. Sin embargo, es de notar que el modelo en [³⁰] es para el diagnóstico de la enfermedad, solo describe la dinámica de la glucosa en la sangre y no involucra la dinámica de insulina, primordial para llevar un control terapéutico de la diabetes, el cual es el objetivo del presente trabajo.

En cuanto a la aplicación de la teoría de control óptimo al problema de la diabetes, en la literatura se encuentran trabajos como los de [²⁹] y [¹³] donde se plantea, en base al modelo de [¹], un problema de control de lazo cerrado que minimiza la variaciones de la glucosa en la sangre con respecto al nivel presente y penaliza las grandes dosis de insulina inyectada. La solución exacta del control se obtiene solucionando un sistema no lineal de ecuaciones algebraicas de Riccati asociado. De los resultados en [¹³] se concluye que el plan de administración de insulina que da lugar a una reducción a niveles aceptables de glucosa, es aquel que está coordinado con los niveles de azúcar en la sangre después de las comidas. En otra línea de investigación la técnica de control predictivo por modelo ha sido empleada en [²⁵], donde se calcula que la dosificación de la insulina a ser inyectada en intervalos de tiempo suficientemente pequeños tal que minimice el error entre el nivel de glucosa de referencia y la curva estimada de la glucosa; sin embargo no hay una demostración formal de su estabilidad. Con el objetivo de incorporar el retraso del efecto de la insulina en disminuir el nivel de glucosa, en [²⁸] basado en el modelo de [¹⁵], se formula un sistema de ecuaciones difereniales con retraso para un problema de control de lazo abierto; se demuestra la existencia y estabilidad de soluciones periódicas y se evidencia a partir de simulaciones que una terapia de inyección de pequeñas dosis de insulina y frecuentes es mucho más efectiva, que aquella de grandes dosis y baja frecuencia. En [¹⁹] se aplica una estrategia inversa de control óptimo vía la función de Lyapunov para pacientes con diabetes mellitus tipo 1. Además se emplean redes neuronales para identificar la dinamica no lineal de la concentración de glucosa como respuesta a la alimentación e infusión continua de insulina, superando la falta de información aportada por el paciente. Los resultados muestran que la regla de control previene eventos de hiperglucemia e hipoglucemia. Sin embargo la ley de control propuesta se encuentra via simulaciones y no hay una deducción análitica de esta.

Recientemente el problema de determinar la magnitud e instantes de aplicación de las inyecciones de insulina que controle la concentración de glucosa en la sangre de un paciente diabetico tipo 1, sujeto a perturbaciones de la vida diaria como la toma de alimentos, ejercicio y stress, es estudiado en [²¹]. Este problema es visto como un problema de optimización de parámetros sujeto a un sistema de cinco ecuaciones diferenciales ordinarias y es resuelto implementando un algoritmo que soluciona la condiciones necesarias de optimalidad correspondiente, derivadas de emplear métodos variacionales clásicos [²⁶]. Concluye que, con la administración de al menos de tres dosis de insulina, menor será la hiperglucemia grave y mejor el manejo del riesgo de hipoglucemia para el paciente. Por otra parte, en [⁴] y [³¹] se emplea un controlador proporcional, integral y derivativo (PID), el cual basado en el error actual, los errores pasados, y la predicción de los errores futuros de los niveles de glucosa en la sangre, se busca mantener estos en el rango saludable, ajustando por medio de un control la cantidad de insulina a ser inyectada. Puesto que en general el controlador PID no es realmente apropiado para sistemas no lineales [³²], en [⁴] consideran la linealización del modelo presentado en [¹⁶] alrededor del nivel basal de glucosa en la sangre, bajo una sola toma de alimento y una sola inyección de insulina. Esto, aunque tiene la ventaja de simplificar la configuración del controlador PID, al eliminar la interacción no lineal entre glucosa e insulina el modelo deja de contemplar fenómenos observados en el organismo como: el retraso de la insulina para actuar y el decaimiento natural de la glucosa que ocurre durante una sola comida; además de que el controlador no asegura el rendimiento deseado para un entorno cambiante como lo puede ser los hábitos alimenticios y la actividad física [²⁴]. Más aún, de los resultados en [⁴] se observa que la evolución temporal de la glucosa bajo el control PID permanece una gran cantidad de tiempo (30 min) en la región hipoglucémica, lo que puede provocar hasta la perdida de la conciencia del paciente.

Al contrario de [⁴], [²¹] y [²⁸], en este artículo se propone un modelo para el suministro continuo de insulina a un paciente diabético, como un problema de control óptimo, teniendo en cuenta particularidades como el tipo de diabetes y algunas características de los hábitos alimenticios. Para describir la dinámica glucosa-insulina consideramos el sistema de dos ecuaciones diferenciales no lineales presentado en [¹⁶]. La ventaja de este modelo radica en su simplicidad, pues contempla los factores principales que afectan la concentración de glucosa en la sangre, es así, que incluye un término no lineal (tipo presa depredador) que representa interacción entre la glucosa y la insulina; la ingesta de comida; aportes externos de insulina en el caso de pacientes diabéticos y especialmente, el rol que desempeña el hígado como reserva de glucosa para mantener los niveles de esta en el torrente sanguíneo, sin llegar a la complejidad de los modelos propuestos en [¹⁸] o en [²¹]. Cabe notar que no se encontraron trabajos previos que estudien la existencia y unicidad de la solución del modelo en [¹⁶], lo cual es uno de los objetivos del presente trabajo.

La gran ventaja del enfoque de control óptimo, que presentaremos, es que no requiere ajustes para cumplir con el objetivo planteado, como ocurre en el diseño y configuración de los controladores PID, pues en esta metodología es necesario ajustar los parámetros del controlador mediante reglas empíricas como lo son: Ziegler-Nichols, Chien, Hrones y Reswick [³²], además de la necesidad de adicionar un controlador de pre alimentación de insulina al control de retroalimentación PID para tratar de contrarrestar las grandes variaciones pos alimentación de la glucosa en la sangre [³¹] y [⁴]. Es así, que el método de control óptimo planteado en este artículo es mucho más directo.

El problema de control óptimo propuesto se analiza matemáticamente, demostrando la existencia del control óptimo. Este control se determina de manera directa solucionando el problema de optimización no lineal asociado mediante el método de programación cuadrática secuencial (SQP). Luego llevamos a cabo simulaciones que sugieren las dosis que ha de suministrar una bomba de insulina durante 24 horas, para tres diferentes escenarios que combinan tipo de diabetes que padece el paciente, estilo de alimentación y nivel de glucosa deseada.

2 Funcionamiento del sistema glucosa- insulina

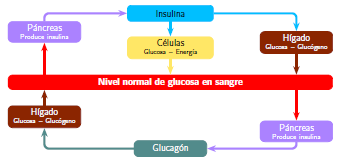
Para que la glucosa pueda entrar en las células y sea utilizada como energía, se requiere de la mediación de la insulina. La insulina es una hormona producida por las células beta del páncreas, la cual es secretada una vez se detecta la presencia de glucosa en la sangre proveniente del proceso alimenticio. Su objetivo es actuar como una "llave que, encajada en la cerradura", abre la puerta de la célula para el paso de la glucosa hacia su interior.

Figura 1 Esquema funcionamiento y producción de insulina. 

El uso de la glucosa hecho por las células, hace que sus niveles de concentración en la sangre se reduzcan hasta alcanzar una concentración normal o de equilibrio. Sin embargo, en situaciones donde el organismo exige un aporte considerable de energía, la concentración de glucosa en sangre puede llegar a ser inferior al nivel normal. En este caso, el páncreas recibe una señal para que las células alfa reaccionen secretando la hormona glucagón, cuya función es provocar la liberación de la glucosa reservada por el hígado hasta que el sistema alcance de nuevo sus niveles de concentración normal.

El páncreas y el hígado trabajan conjuntamente utilizando un sistema de equilibrio y control para mantener los niveles de glucosa e insulina en niveles saludables. Así pues, el cuerpo humano debe tener la capacidad de mantener un estricto control sobre la glucosa. Según la Asociación Americana de Diabetes (ADA, por sus siglas en inglés), los niveles de glucosa en el organismo, antes de comer, están entre 90 y 130 mg/dl, y después de comer deben ser menores a 180 mg/dl en personas sanas. Cuando se presenta un mal funcionamiento de este sistema, es muy difícil mantener estos niveles en el margen apropiado, y este mal funcionamiento es básicamente lo que se conoce como diabetes.

3 Tratamiento de la diabetes

La deficiencia de insulina, así como la imposibilidad de aprovechar aquella que se produce naturalmente, requiere que la administración de insulina exógena sea necesaria. Así pues, el tratamiento de los pacientes que padecen de diabetes se realiza a través del ejercicio, una dieta sana y el aporte externo de insulina de manera artificial que se inyecta en la sangre. Estas inyecciones se realizan con diferentes dispositivos, jeringas y bombas. De acuerdo con [³], uno de los problemas que se presenta en todos los dispositivos de administración, es que estos deben ser controlados por el paciente, lo que implica que las dosis de la hormona no siempre se suministre cuando se necesita, o que las dosis sean muy altas o muy bajas para los procesos metabólicos que se llevan a cabo. Es por esta razón que solucionar este problema requiere la creación de un tipo de tratamiento, en el cual el dispositivo actúe de forma autoregulada y el paciente no necesite estar atento de proporcionar las cantidades de la hormona que considera correctas para el manejo de su enfermedad.

3.1 Concentraciones de glucosa e insulina para personas sanas y diabéticas

La glucemia es la medida de concentración de glucosa en sangre, suero o plasma sanguíneo. Esta medida se presentan usualmente en unidades de concentración molar (mmol/L), o en unidades de concentración de masa (mg/dL). En la tabla 1 se presentan las concentraciones de glucosa que se consideran normales o saludables, tanto para personas sanas como para diabéticas, establecidas por la ADA.

Tabla 1 Concentraciones de glucosa normales para personas sanas y diabéticas. 

Por otra parte, las concentraciones de insulina pueden ser reportadas en unidades de concentración molar (pmol/L) o en número de unidades por unidad de volumen (µU)/mL. En 1987, la OMS determinó que un gramo de insulina es equivalente a 26 000 unidades de la hormona (esta equivalencia es llamada la potencia) [¹⁴]. Sabiendo que el peso molecular de la hormona es 5808 g/mol, se deduce que la masa de una unidad de la hormona es de 3,85 X 10^-5 g, y por lo tanto una unidad equivale a 6,62 X 10^-9 moles. Finalmente, haciendo la conversión entre unidades y microunidades (µU) se tiene que 1 µU es equivalente a 6,62 x 10^-15 moles, y de aquí se concluye que 1 µU/mL es equivalente a 6,62 x 10^-12 moles/L, o 6,62 pmol/L. Sin embargo, según [¹⁷], este cálculo puede ser incorrecto al tomar como base el valor de una masa molar impreciso (la insulina puede estar impura al tener presencia de agua y sales), o por aplicación redondeos mal elaborados, por lo que se considera que el factor de conversión correcto, además de ser el más utilizado en el ámbito médico es 1 µU/mL = 6,00 pmol/L.

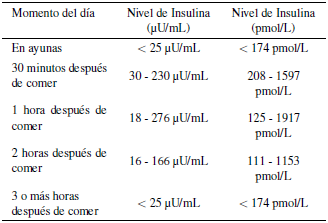
La tabla 2 contiene los valores saludables o normales para la concentración de insulina, en diferentes momentos del día.

Tabla 2 Concentraciones de insulina saludables, en diferentes momentos del día. 

4 Modelo matemático

A partir de la descripción del mecanismo de regulación de la glucosa expuesto en la sección 2, en [¹⁶] se propone el siguiente sistema de ecuaciones diferenciales para la dinámica de la regulación de la glucosa en el cuerpo, que considera el rol del hígado como proveedor de glucosa almacenada (glucógeno)

donde g(t), h(t) denotan los niveles de glucosa e insulina en el flujo sanguíneo en un tiempo t respectivamente. Los valores iniciales g ₀ y h ₀ sonlos niveles basales (en ayuno) de la glucosa e insulina y los parámetros a ₁ , a ₂ , a ₃ , a ₄ , b ₁ y b ₂ son constantes positivas.

En la ecuación (1a), el término -a ₁ gh representa el decrecimiento de los niveles de glucosa en el organismo debido a la transformación de la glucosa en energía para las células por la mediación de la insulina. Ahora bien, denotando la parte positiva de una función por (^.)+, la expresión a₂(g₀ - g) ⁺ describe la acción del hígado que secreta la glucosa almacenada cuando su concentración está por debajo del nivel basal g₀, mientras que, -a₃(g - g₀)⁺ se refiere a que el nivel de glucosa decae naturalmente proporcional a su exceso sobre el nivel de ayuno g ₀ . La función continua, acotada y positiva p(t) representa el ingreso de glucosa externa al sistema por la ingesta de alimentos, esta será descrita con mayor detalle en el apartado 6.2.

En cuanto a la razón de cambio de la insulina, ecuación (1b), el primer término del lado derecho describe el aumento de insulina en el cuerpo debido al exceso de glucosa en la sangre por encima del nivel de ayuno g ₀ . El segundo término representa la degradación natural de la insulina.

4.1 Existencia y Unicidad de la solución

Teorema 4.1. Sea D un subconjunto abierto de [0, T] X ℝ² sobre el cual está definido el PVI (1) con (t ₀ , g ₀ , h ₀ ) ∈ D. Entonces para algún r > 0 existe una única solución (g(t),h(t)) definida en el intervalo I = [t ₀ - r, t ₀ + r].

Prueba. Por la forma en la que están definidas las funciones (g - g ₀ ) ⁺ y (g0 - g)⁺, deben estudiarse los siguientes casos:

Caso 1. Si g < g0,

Caso 2. Si g0 = g,

Caso 3. Si g0 < g,

Ahora, denotemos con f ≡ f (t, g, h) el lado derecho de cada sistema de ecuaciones diferenciales, observamos que para cada uno de los tres casos ambas componentes de f son polinomios en las variables g y h, es decir, f G ∈^0,∞ ([0, T] x ℝ²; ℝ²); por lo que f es una función localmente Lipschitz con respecto a (g, h) ∈ ℝ². Finalmente, el teorema Picard-Lindelöf garantiza que dado cualquier valor inicial (g ₀ , h ₀ ) ∈ D existe una única solución del sistema de ecuaciones diferenciales (1) en el intervalo I. □

En lo que sigue probamos que la solución del sistema (1) existe globalmente.

Teorema 4.2. Para cualquier condición inicial positiva (g ₀ , h ₀ ), el sistema de ecuaciones diferenciales (1) tiene solución global.

Prueba. Para garantizar la existencia de la solución de (1) para todo t ≥ 0, es suficiente probar que f (t, g, h) crece a los más linealmente con respecto a ( g, h). En efecto, considerando de nuevo los tres casos anteriores tenemos:

Caso 1 g ₀ > g: De la ecuación (2b), h(t) = h ₀ e ^-b2t , entonces 0 < h(t) ≤ h ₀ para todo t ≥ 0. Reemplazando h(t) en (2a), obtenemos

Luego el lado derecho de (2) es acotada linealmente en g. Entonces toda solución de (2a) es global.

Caso 2 g ₀ = g: De manera similar al caso anterior tenemos que la solución de (3b) es global y 0 < h(t) ≤ h0 para todo t ≥ 0. Además de la ecuación

para todo t ≥ 0. Por lo tanto g(t) está definida para todo t ≥ 0.

Caso 3 g 0 < g: La solución de la ecuación (4b) está dada por

puesto que g(t) - g0 ≥ 0, entonces h(t) ≥ 0 para t ≥ 0. Ahora, podemos sumar las ecuaciones del sistema (4) y obtenemos

Luego g(t)+h(t) es acotadalinealmente. Porlotanto, las soluciones g(t) y h(t ) existen para todo t ≥ 0. □

Nótese que el resultado del teorema 4.2 implica que la soluciones del sistema (1) son acotadas superior e inferiormente para todo intervalo [0, T].

5 Problema de control óptimo para el sistema glucosa-insulina

Es claro que la dinámica entre la glucosa y la insulina es diferente entre pacientes diabéticos y no diabéticos, por lo cual el problema de control óptimo consiste en influenciar la dinámica de un paciente diabético, para que esta se comporte de manera similar a la de un paciente no diabético o sano.

Así pues, se estudiará el caso de un paciente enfermo de diabetes que no produce de manera natural la cantidad de insulina necesaria para aprovechar la glucosa adecuadamente, es decir, la sensibilidad del metabolismo a la presencia de glucosa es muy pequeña i.e., b₁ ≈ 0, razón por la que el paciente requerirá del aporte externo de insulina en el tiempo, representado por la función u(t). Lo anterior implica que la segunda ecuación (1b) del sistema (1) se transforme en:

Como se desea que este suministro de insulina externa sea lo más pequeño posible tal que la concentración de glucosa se mantenga muy cercanaa un nivel de concentración deseado gd , el problema de control óptimo consiste en minimizar el funcional:

Sujeto a:

donde ū es la concentración promedio de insulina en sangre de un paciente sano durante un tiempo de 24 horas, g _min y g _max son las concentraciones mínima y máxima respectivamente de glucosa saludable en el organismo de una persona diabética (ver tabla 1), y umin, umax son las restricciones del control, que en el contexto del problema, corresponden a los valores máximo y mínimo de insulina exógena que pueden ser suministrados a un paciente diabético.

5.1 Existencia de una solución para el problema de control óptimo

La prueba de la existencia del control óptimo se basa en el resultado estándar presentado en [⁶] (véase teorema 1.1 páginas 36-38). A continuación presentamos una versión de este resultado adaptado al problema de control óptimo para el sistema glucosa-insulina (8)-(13). Sean L(t, g, u) el integrando del funcional (8), U el intervalo cerrado [u _min , u _max ] y f (t, x, u) el lado derecho del sistema de ecuaciones diferenciales (9) -(10) conx =[g(t),h(t)] ^T .

Teorema 5.1. Si el problema de control óptimo (8)-(13) satisface las siguientes condiciones:

a) La función L: [0, T ] x ℝ x ℝ → ℝ es medible en t, continua en (g, u) y u → L(t, g, u) es convexa para todo (t,g) ∈ [0, T] x [0,g_max]; U(t) = U ⊆ R es cerrado y convexo. La función hamiltonianaH(t,g,q) = sup{q• v -L(t,g,v);v ∈ U}, satisface la condición de crecimiento:

Donde σ, γ ∈ L ¹ (0, T), µ(.,p) ∈ L ¹ (0, T) para todo q ∈ ℝ y sup {µ(t,q); ║q║ ≤ δ} ∈ L ¹ (0, T) para cada δ > 0.

b) La función f(t, x, u) puede escribirse de la forma f (t, x, u) = f ₀ (t, x) + f ₁ (t, x)u, con x = (g,h), ∀(t,x, u) ∈ [0, T] x ℝ² x ℝ, tal que f ₀ , f ₁ son funciones continuas en x, medibles en t y además, para t ∈ (0, T) y x∈ ℝ²

donde α ₀ , β ₀ ∈ L¹(0, T), α₁ ∈ L ^∞ (0, T) y α _δ ∈ L ¹ ( 0, T) para todo δ > 0,

entonces tiene al menos una solución (g*,h*,u*) en el espacio de todas las funciones continuas en ([0, T ] x ℝ²) x L¹(0, T ; ℝ).

Prueba. a) Puesto que L(t, g, u) = (g(t) - gd) ² + (u(t) - ū) ² es la composición de funciones continuas en t, entonces L es Lebesgue-medible en t. Además L es la suma de dos funciones cuadráticas una en g y otra en u, por lo cual, L es continua en (g, u) y convexa; en particular, como función de u para todo (t, g) ∈ [0, T ] x [0, g _max ].

Claramente la desigualdad (14) se satisface, puesto que v(t) ∈ U y donde ß(t, q) = u _max |q|, σ (t ) = 0, γ(t ) = 0. Además, las funciones µ, σ y γ son L¹([0, T}) y por lo tanto sup{µ(t, p); ║q║ ≤ δ} ∈ L¹(0, T) para cada δ > 0.

b) Sean:

Denotemos con x = (g, h) ^T , luego f (t, x, u) = f ₀ (t,x)) + f ₁ (t,x)u(t). Además, por los teoremas anteriores sabemos que g, h∈C ¹ ([0,T], ℝ) para todo T > 0 y f0(t, (g,h)) y f1(t, (g,h)) son funciones continuas en (g, h), por lo tanto f ₀ y f ₁ son medibles en t.

Para probar la desigualdad (15) empleamos la equivalencia entre normas en ℝ² y la desigualdad de La desigualdad de Cauchy-Shwartz, es así que

Ahora consideremos los siguientes dos casos:

La desigualdad (16) se obtiene claramente de que

║f1(t, x)║ _∞ = 1.

Con respecto a la desigualdad (17), consideramos los siguientes dos casos

• Si ║f ₀ (t, x)║ _∞ = ║- α₁ gh +α₂(g ₀ -g)⁺- α ₃ g-g ₀ )⁺ + α₄ p(t)║_∞ entonces de la desigualdad triangular y dado que ║x║_∞ ≤ δ resulta ║f ₀ (t,x)║ ≤ α _δ (t). Donde α _δ (t) = (α1║g║_∞ + α ₂ -α ₃ ) δ + α ₄ ║ p(t)║ _∞

• Si ║f ₀ (t, x)║ _∞ = ║b₁ (g - g ₀ ) ⁺ - b ₂ h║_∞, procedemos como en el caso anterior y obtenemos que ║ f ₀ (t, x)║ ≤ 2(b ₁ +b ₂ )δ, para todo t ∈ (0, T) y x ∈ ℝ² tal que ║x║ ≤ δ.

Finalmente, las funciones α₀, β₀ y α_δ pertenecen a L ¹ (0, T), puesto que son funciones constantes. La función o 1 pertenece a L ^∞ (0, T) ya que también es una función constante, y p(t) es continua en [0, T]. Como las condiciones a) y b) se satisfacen, entonces existe al menos una solución para el problema de control óptimo (8)-(13). □

6 Solución Numérica

Para resolver el problema de control óptimo de manera directa, discretizamos las variables de estado, de control y el funcional, de tal forma que el problema se reduce a un problema de programación no lineal (PNL). Este, lo resolvemos mediante el método de programación cuadrática secuencial (SQP por sus siglas en inglés) [23].

6.1 Discretización del problema de control óptimo

Para la discretización del problema (8)-(13) procedemos de la siguiente manera:

• 1. En el intervalo [0, T] se consideran N +1 puntos equidistantes t _k = kΔt, k = 0,1,...,N, con Δt= T/N.

• 2. La función de control u(t) se aproxima por su interpolación lineal sobre cada subintervalo [t _k , t _k+1],esto es

donde uk = u(t _k ) y u _k-1 = u(t _k+1 ).

• 3. Se considera el vector de estado x = (x0,..., x _n ) ^t ∈ ℝ ^2(N+1) con x _i =(g(t _i ),h(t _i )) ^T ,i=0,...,N.

• 4. La integral de la función objetivo (8) se discretiza mediante la regla de cuadratura rectangular izquierda.

• 5. El sistema de ecuaciones diferenciales (9)-(10) se resuelve por método de Runge-Kutta de cuarto orden [¹¹].

De lo anterior, se obtiene el problema de programación no lineal

Sujeto a:

donde x _k = (g _k , h _k ), y F ₁ , F ₂ representan las trayectorias de la variable de estado que resultan de la solución por integración numérica del sistema de ecuaciones diferenciales definido en (9)-(10), usando el esquema de Runge-Kutta cuarto orden.

Finalmente, resolvemos el problema de programación no lineal (21) mediante el método de programación cuadrática secuencial. Para más detalles ver [²³].

6.2 Aspectos generales de las simulaciones

A continuación se mencionan algunos aspectos generales que se tienen en cuenta para la construcción de las simulaciones en los diferentes escenarios considerados:

• 1. Punto de equilibrio basal: De acuerdo con la tabla 1, en todas las simulaciones tanto de pacientes diabéticos tipo 1 como tipo 2, se toma el valor de 100 mg/dL (5,56 mmol/L) como el punto de equilibrio alrededor del cual se intenta estabilizar el sistema (1) y que corresponde con su valor inicial, es decir, g0 = 100 mg/dL y h₀ = 2.7 µ/mL. Estos valores se usan en el esquema numérico que permite encontrar las trayectorias de las variables de estado definidas por las dos primeras ecuaciones en (22).

• 2. límites de glucosa en sangre: De igual manera, de acuerdo con la tabla 1 se utilizarán como concentraciones saludables de glucosa en sangre (o límites de normoglucemia) los valores 60 y 180 mg/dL. Por lo tanto, g _min = 60 mg/dL y g _max = 180 mg/dL en (22)

• 3. Límites de la insulina suministrada: El control óptimo (dosis de insulina suministrada por la bomba) debe estar restringido, de acuerdo con la formulación del problema presentada en (8)-(13). Esto debido a que en el contexto del problema que se pretende resolver en este trabajo, los valores de insulina exógena no tienen sentido si son negativos, ni tampoco podrá tomar valores superiores a 100 µ/mL, puesto que podría causar una hipoglucemia al paciente. Luego, consideramos u _min = 0 (µU/mL) y u _max = 100 (µU/mL) en (22).

• 4. Tiempo de toma de muestras: En la actualidad, ya se dispone de sensores de glucosa que permiten conocer los niveles de glucosa en sangre cada 5 minutos [⁵]; así que el problema se resuelve para los diferentes escenarios simulados en un intervalo de tiempo de [ 0, 24] horas, con un paso de discretización Δt = 24/288.

• 5. Glucosa deseada (g _d ): El término g _d en (21) representa la concentración de glucosa que se desea tuviese el paciente en cada instante del día que se simula. Con el fin de considerar algunas alternativas, que permitan comparar y discutir los resultados obtenidos, se usarán dos tipos de glucosa deseada. En el primer caso, los niveles de glucosa deseada están dados por la solución numérica del sistema (1) con parámetros de un paciente sano, estos son (a₁ = 0.05, a₂ = 1, a ₃ = 0.03, a₄ = 4, b ₁ = 0.5, b ₂ = 2). En el segundo caso, (g _d ) toma un valor constante que se obtiene del promedio de los niveles de glucosa para un paciente sano durante las 24 horas.

• 6. Comidas: Suponemos que la glucosa externa que ingresa al sistema en cada comida, se mezcla con toda la sangre del cuerpo instantáneamente y produce una alta concentración de esta en todas partes que eventualmente decae exponencialmente. Esto se describe con la función

• donde el parámetro Q _i representa la cantidad de carbohidratos que se consumen en cada comida (desayuno, almuerzo, cena, onces y/o merienda), y el parámetro τ_i, i = 1,2,...,5 indica la hora del día en la que es consumido el alimento. En cada uno de los escenarios simulados se indicará con detalle el menú junto con la cantidad total de carbohidratos y la hora del día en la que se consumen. Los menús contemplados en cada escenario de alimentación son de invención propia, complementados con información disponible en [²⁰] y con ayuda de calculadoras de dieta disponibles en la web, como las que se encuentran alojadas en [²²] y [¹²]. En las dietas 7. consideradas en cada escenario, se referencia solamente la cantidad de carbohidratos (en gramos) que son consumidos por la persona en cada porción consumida, totalizando al final la cantidad de carbohidratos a consumir por comida. No se hace referencia al peso total por porción, porque esta información no es relevante ni necesaria en los análisis y estudios del presente trabajo.

• 7. Características del cómputo: Las simulaciones presentadas en este capítulo fueron elaboradas usando el software Matlab® versión 2019a, instalado en un computador con procesadorAMD®Ryzen™ 5 2500U 3.6 GHz y una memoria RAM de 8 GB.

Tabla 3 Parámetros del sistema (1) identificados y concentraciones máximas alcanzadas de glucosa en mg/dl e insulina en µU/ml para cada escenario y tipo de diabetes sin control 

7 Resultados y discusión

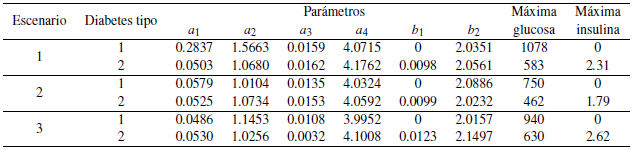
En esta sección se presenta la simulación de tres distintos escenarios de pacientes diabéticos tipo 1 y tipo 2 bajo un posible estilo de alimentación sin considerar inicialmente el ingreso de insulina exógena. En cada escenario se consideró un conjunto de datos que representa los niveles reales de glucosa e insulina en sangre para diferentes instantes de tiempo t en un día (t G [0, ²⁴]) y que se emplean para identificar los parámetros del modelo (1) mediante la solución de un problema no lineal de mínimos cuadrados usando el método de Gauss-Newton [²³], los resultados se presentan en la tabla 3. Una vez ajustados los parámetros se resuelve el problema de control óptimo que indicará la cantidad de insulina exógena a ser suministrada por la bomba o el dispositivo electrónico que cumpla estas funciones. En seguida, se presenta la gráfica del comportamiento de la dinámica glucosa-insulina, junto con la gráfica del alimento y la cantidad de insulina a ser inyectada (función de control).

7.1 Escenario 1: dieta no muy rigurosa

Aquí se contempla la ingesta de 4 comidas (desayuno, almuerzo, cena y onces) para el caso de un paciente que no es muy riguroso con el conteo de la cantidad de carbohidratos que consume, pero procura que no sea muy alta. El menú considerado se presenta en la tabla 4.

7.1.1 Diabético tipo 1

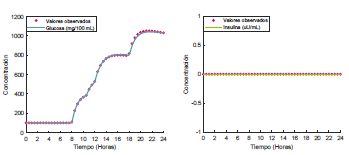
Figura 2 Dinámica glucosa-insulina de un paciente diabético tipo 1 sin suministro exógeno de insulina. valores estimados de los parámetros a₁ = 0.2837, a₂ = 1.5663, a₃ = 0.0159, a₄ = 4.0715, b₁ = 0 y b₂ = 2.0351. 

Observe que sin suministro de insulina exógena a un paciente diabético tipo 1, la concentración de glucosa en sangre puede alcanzar niveles cercanos a los 1000 mg/dL, tal como se aprecia en la figura 2. Esto es peligroso para el paciente, no solo por el daño que niveles tan elevados de glucosa puedan causar a los órganos del cuerpo, sino por el riesgo del paciente de sufrir una cetoacidosis diabética que lo enviaría a una sala de urgencias, si no se logra disminuir el nivel de glucosa en cuestión de minutos.

Tabla 4 Menú escenario 1. 

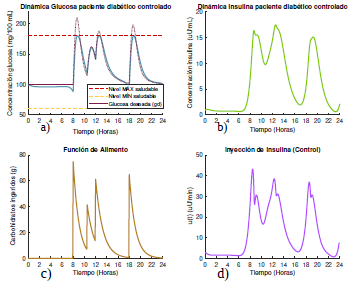
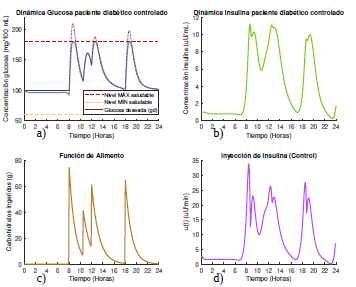
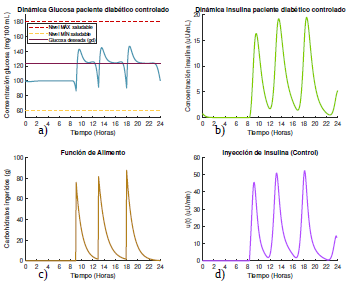
Figura 3 Dinámica de glucosa e insulina bajo control óptimo con glucosa deseada según la opción 1 para un paciente diabético tipo 1 que se alimenta según el escenario 1. 

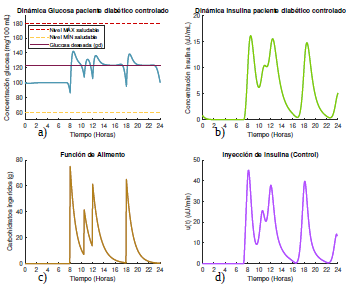
Figura 4 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 1 que se alimenta según el escenario 1, con glucosa deseada según la opción 2. 

En la figura 3 se observa que al suministrar la insulina exógena, esta actúa y logra mantener la concentración de glucosa del paciente dentro del rango de normoglucemia ([60 mg/dL, 180 mg/dL]),evitando así que el paciente presente episodios de hiper o hipoglucemia durante todo el día. Sin embargo, nótese que a diferencia de un paciente sano, donde la insulina actúa con cierto retraso sobre la dinámica de la glucosa, para el caso del paciente diabético esta debe empezar a actuar unos minutos antes de que el nivel de glucosa empiece a elevarse, para mantener la concentración por debajo del nivel máximo permitido. La cantidad máxima de insulina exógena suministrada durante todo el día es de 44. 35 µU/mL.

Note además que, cuando la glucosa deseada es dada por la dinámica del sistema (1) para un paciente sano, la concentración de glucosa es más alta y permanecen más cercana al límite máximo permitido como se observa en la figura 3a. Sin embargo, esta elección de la glucosa deseada requiere mucha menos cantidad de insulina a ser suministrada para mantener los niveles de glucosa dentro los límites saludables, aunque requiere que pequeñas dosis de insulina sean inyectadas durante las primeras 7 horas y media del día (figura 3d). En total se necesitaron 2422 µU/mL distribuidas a lo largo de las 24 horas del día para mantener la glucosa totalmente controlada. Por su parte, cuando la glucosa deseada se toma constante g _d = 125 mg/dl (figura 4a), la concentración de la glucosa en el torrente sanguíneo del paciente permanece muchísimo más baja.

Aquí el algoritmo de optimización calcula las cantidades de insulina que se requieren para que el nivel de glucosa se mantenga lo más cercano posible a la concentración de glucosa deseada, representada con la línea punteada en la figura 4a), y es por esta razón que entre las 2 y las 4 pm, la dinámica de la glucosa tiende a mantenerse constante decayendo solo cuando se aumenta la cantidad de insulina que se suministra unos minutos antes de ingerir el alimento. No obstante, como la glucosa deseada puede llegar a ser muy restrictiva, la cantidad de insulina que debe suministrarse para mantener la concentración de glucosa cercana a la deseada es mayor en este caso, donde es necesario inyectar 2727 µU/mL distribuidas a lo largo de las 24 horas del día (figura 4d).

7.1.2 Diabético tipo 2

En este caso, a diferencia del paciente diabético tipo 1, los niveles de glucosa alcanzados sin el suministro de insulina exógena no superan el valor de 600 mg/dL, esto debido a que las personas que padecen este tipo de diabetes sí producen insulina como se aprecia en la figura 5 pero la cantidad producida es insuficiente o no puede aprovecharse eficientemente.

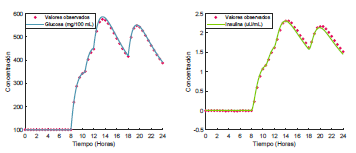
Figura 5 Dinámica glucosa-insulina de un paciente diabético tipo 2 sin suministro exógeno de insulina. Valores estimados de los parámetros α₁ = 0.0503, α₂ = 1.0680, α₃ = 0.0162, α₄ = 4.1762, b₁ = 0.0098 y b₂ = 2.0561. 

El suministro de insulina exógena (control) que proporciona la bomba a lo largo del día, se ilustra en las figura 6d y 7d. En las ^{figuras 6a} y ^7a se observa que los niveles de glucosa han bajado quedando entre los límites permitidos, tendiendo siempre a estar muy cerca a la concentración de glucosa deseada. Además, nótese que la cantidad de insulina inyectada es más baja que la cantidad suministrada para el paciente diabético tipo 1, ya que el paciente tipo 2 produce insulina de manera natural y es utilizada también la metabolización de la glucosa.

Con respecto a las dos diferentes formas de selección de la glucosa deseada, en este caso se observan comportamientos muy similares a los observados para el caso del paciente diabético tipo 1. Para la primera forma de selección de la glucosa deseada la concentración del paciente se mantiene más alta pero dentro de los niveles máximo y mínimo permitidos, tendiendo a estar siempre muy cercanas (figura 6a), y para la segunda forma de selección de glucosa deseada (figura 7a), la concentración del paciente se mantiene en niveles mucho más bajos que en la primera forma, debido a que el problema de control óptimo busca minimizar la distancia entre la concentración de glucosa del paciente y la glucosa deseada, que en este caso tiene un valor constante cercano al nivel basal.

Además, al igual que para el paciente diabético tipo 1, aquí también la primera forma de selección de glucosa deseada implica un suministro menor de insulina, como se observa al comparar las gráficas del control de cada caso (figura 6d y figura 7d).

Figura 6 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 1, con glucosa deseada según la opción 1. 

7.2 Escenario 2: dieta baja en carbohidratos

En la mayoría de los casos, muchos pacientes diabéticos deben complementar su tratamiento para la diabetes con dietas bajas en carbohidratos. En este escenario se considera un estilo de alimentación que consta de 5 comidas, todas estas muy bajas en carbohidratos, lo que no significa que los pacientes deban comer pequeñas porciones o diseñar menús que contengan solo verduras (véase tabla 5).

Tabla 5 Menú escenario 2 

En este escenario, la dinámica de la glucosa e insulina para pacientes diabéticos sin suministro exógeno de insulina, es cualitativamente similar a la presentada en el escenario 1 (ver figuras 2 y 5). Para este caso, a pesar de que el paciente sigue una dieta muy cuidadosa, este alcanza un nivel de glucosa superior al permitido. Es así, que el paciente con diabetes tipo 1 llega a una concentración máxima de 750 mg/dl mientras que aquel con diabetes tipo 2 alcanza 450 mg/dl (véase tabla 3).

En las figuras 8a), 9a), 10a) y 11a), se aprecia que efectivamente se logró reducir los niveles de glucosa en sangre a partir del suministro de insulina exógena calculado como solución del problema de control óptimo. Incluso las concentraciones de glucosa se mantienen muy por debajo de 180 mg/dL, además de que la cantidad de insulina empleada es mucho menor que la requerida en la reducción de los niveles de glucosa de pacientes con estilos de alimentación similares al del escenario 1. Estos resultados permiten validar el hecho de que una dieta baja en carbohidratos funciona muy bien como parte del tratamiento de la enfermedad de un paciente diabético.

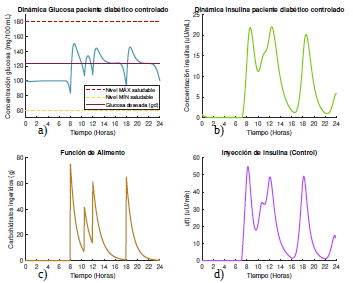
Figura 7 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 1, con glucosa deseada según la opción 2. 

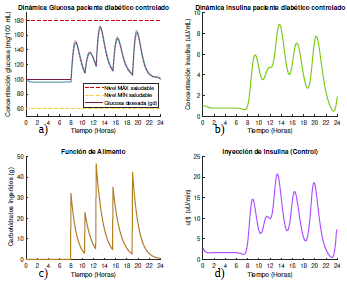
Figura 8 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 1 que se alimenta según el escenario 2, con glucosa deseada según la opción 1. 

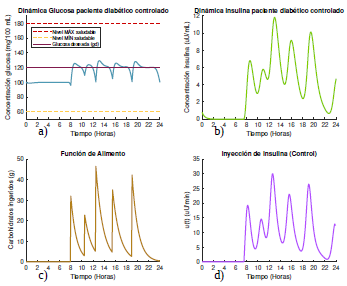
Figura 9 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 1 que se alimenta según el escenario 2, con glucosa deseada según la opción 2. 

En cuanto a la comparación entre los dos tipos de pacientes diabéticos considerados en la simulación, el comportamiento de la dinámica de la glucosa como el de la insulina resultaron ser muy parecidos en ambos tipos de paciente. Aunque, como era de esperarse, el paciente diabético tipo 1 requerirá mayor cantidad de suministro de insulina durante todo el día. Esto sugiere entonces que el parámetro b ₁ del modelo (1) no es sensible a los pequeños cambios que se realice sobre los valores que toma.

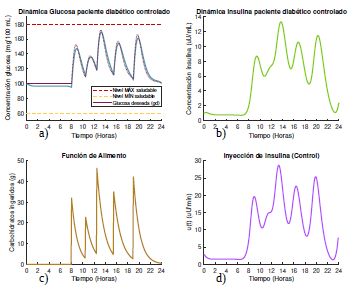
Figura 10 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 2, con glucosa deseada según la opción 1. 

Al centrar la atención en la selección de la forma de la glucosa deseada, en las figuras 8a) y 10a) se observa nuevamente que las concentraciones de glucosa resultantes son más altas que las obtenidas en las respectivas gráficas de las figuras 9a) y 11a), esto debido a la libertad que ofrece la forma 1 de selección de glucosa deseada con respecto a la forma 2 que es bastante restrictiva en la medida en que se obliga a la concentración de glucosa del paciente a estar cercana a un valor constante durante todo el día sin la posibilidad de considerar niveles un poco más elevados.

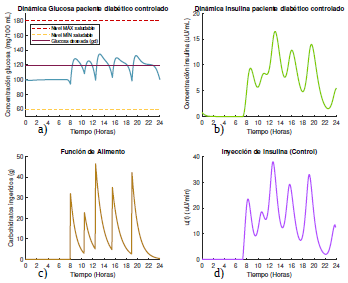
Figura 11 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 2, con glucosa deseada según la opción 2. 

Aquí también se aprecia una ventaja en cuanto a las cantidades de insulina suministrada para el cumplimiento del objetivo al elegir la forma 1 de la glucosa deseada, que es más baja que las necesarias al escoger la forma 2, como se observa al comparar las figuras 8d) y 10d). Además, nótese nuevamente que en la segunda forma de selección de glucosa no es necesario el suministro de insulina durante las primeras 7 horas y media del día.

7.3 Escenario 3: dieta irresponsable

Así como existen pacientes muy responsables con el tratamiento de su enfermedad, que llevan una dieta saludable y son muy cuidadosos con el suministro de las dosis de insulina según las recomendaciones médicas, existen otros pacientes que no son conscientes de su enfermedad y de las graves consecuencias que pueden contraerse de una diabetes mal tratada al no tener en cuenta los cuidados que deberían seguirse. En este escenario se simula el estilo de alimentación de un paciente que no restringe en absoluto la cantidad de carbohidratos que ingiere, al tener una marcada preferencia por el consumo de comida conocida como "chatarra". El tipo de alimentos que ingiere en cada comida se muestra en la tabla 6.

Tabla 6 Menú escenario 3 

La dinámica de la glucosa e insulina sin el suministro exógeno de insulina para este escenario es cualitativamente similar a la presentada en el escenario 1, donde ocurre una acumulación de glucosa en la sangre a través del día (ver figuras 2 y 5). De la tabla 3 en este caso se observa que los niveles de glucosa alcanzan valores 940 mg/dL y 630 mg/dL para el paciente diabético tipo 1 y tipo 2 respectivamente.

En la figuras 12a) y 14a), se observa que una vez aplicado el control óptimo sobre la dinámica glucosa-insulina, se logra que los niveles de glucosa desciendan y se mantengan dentro de los límites de normoglucemia, aunque estos puedan llegar a alcanzar valores de 180 mg/dL hora y media o dos horas después de comer. Sin embargo, la cantidad de insulina a administrar por la bomba es la más grande (alrededor de 60 µU/mL para el paciente diabético tipo 1 y de 58.7 µU/mL para el paciente diabético tipo 2) comparada con la cantidad administrada para los escenarios considerados anteriormente, logrando así mantener dentro de los límites la cantidad de glucosa rezagada que es aportada por la comida ingerida durante el almuerzo y la que ingresa por el consumo de la cena.

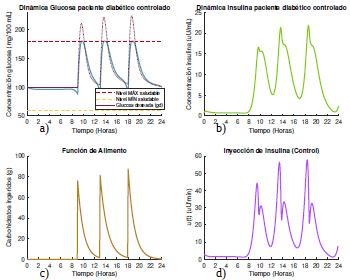
Figura 12 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 1 que se alimenta según el escenario 3, con glucosa deseada según la opción 1. 

Por su parte, en las figuras 13a) y 15a), en las que se eligió la forma 2 de glucosa deseada, las concentraciones de glucosa de los pacientes se mantienen mucho más bajas, quedando alrededor de los 140-150 mg/dL, pero la cantidad de insulina que se requiere es la más alta (llegando a los 58.7 µU/mL y manteniendo esta cantidad por periodos de tiempo más largos), comparada no solo con las cantidades de insulina necesarias en este escenario al seleccionar la forma 1 de glucosa deseada, sino también con los escenarios analizados anteriormente, como se aprecia en las figuras 13d) y 15d).

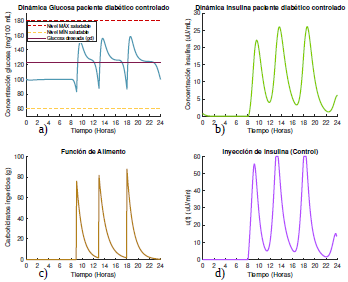
Figura 13 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 1 que se alimenta según el escenario 3, con glucosa deseada según la opción 2. 

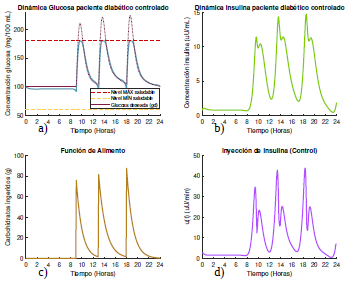
Figura 14 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 3, con glucosa deseada según la opción 1. 

Es importante mencionar, que el valor de insulina máximo que se presentó para este escenario, es menor que la cantidad de insulina exógena máxima suministrada que es reportada en [⁷], la cual oscila alrededor de 80 µU/mL. Esto representa una ventaja del método propuesto en este trabajo, teniendo en cuenta que las funciones que modelan la ingesta de alimento y la cantidad de carbohidratos ingeridos en el único escenario considerado, son similares a las empleadas en [⁷].

Figura 15 Gráficas de las dinámicas de glucosa e insulina, junto con su control óptimo para un paciente diabético tipo 2 que se alimenta según el escenario 3, con glucosa deseada según la opción 2. 

8 Conclusiones

Se exploró y se probó el método de programación no lineal (PNL) como estrategia de solución al problema de control óptimo planteado, cumpliendo con todas las restricciones a las que fue sujeta la formulación del problema, de tal manera que fue posible mantener siempre los niveles de glucosa entre los límites deseados en todos los diferentes tipos de escenarios que tuvieron en cuenta durante el proceso de simulación, sin poner en riesgo, en ningún caso, al paciente de sufrir una hipo o hiperglucemia, tal como puede verse en la sección 7. Estos resultados permiten concluir que el método propuesto es una alternativa efectiva y más directa, frente a la que actualmente se encuentra disponible en el mercado [⁸] (algoritmo de control PID, usado en [³¹]), para el futuro desarrollo y construcción de bombas de administración de insulina cada vez más automáticas en las que se disminuya considerablemente la necesidad de la manipulación del dispositivo por parte del paciente, y así poder avanzar en el diseño y construcción de los llamados "páncreas artificiales".

Se realizaron experimentos con dos tipos de selección de glucosa deseada, donde al seleccionarla de acuerdo a la dinámica de glucosa de un paciente sano a lo largo del día, se obtienen resultados mucho más favorables, con respecto a la cantidad de insulina a ser suministrada, que cuando se selecciona como un valor constante, debido a que este último tiende a ser bastante restrictivo sobre la tendencia que debe seguir la concentración de glucosa del paciente, lo cual por supuesto exige mayores cantidades de insulina que deben ser suministradas para el cumplimiento del objetivo impuesto. Lo anterior sugiere, que puede seleccionarse una glucosa deseada para cada estilo de alimentación del paciente, donde una similar a la forma 1 sería ideal para una persona rigurosa con sus horarios de comida y conteo de carbohidratos ya que siempre se podrá predecir la tendencia del comportamiento de sus niveles de glucosa dependiendo de la cantidad de carbohidratos que desea comer, mientras que la forma 2 de selección de glucosa deseada tal vez resulte mejor en pacientes que comen todos los días a diferentes horas del día y no son cuidadosos con el conteo de carbohidratos. Como se evidenció en el la sección 7, el problema de control óptimo logra resolverse manteniendo siempre las concentraciones de glucosa cercanas al valor constante que se tome como glucosa deseada, sin importar el tipo de comida ni la hora en que se consuma y sin poner el riesgo al paciente de llegar a estar fuera de los límites de glucosa permitidos, pero por supuesto, esto requiere que la cantidad de insulina a suministrar sea más alta.

Por otra parte, es importante en todo caso que los pacientes diabéticos mantengan un estilo de vida saludable, que incluya el consumo de alimentos bajos en carbohidratos, puesto que son los responsables en el aumento de los niveles de glucosa en sangre debido a su consumo excesivo. Seguir las dietas y recomendaciones dadas por los profesionales de la salud, conllevará a que la diabetes sea mejor tratada y la cantidad de medicamento que el paciente deba consumir se reduzca considerablemente, lo que representaría un beneficio económico en la adquisición y compra del fármaco por parte de los sistemas de salud. En este sentido y con el objetivo de predecir un perfil glucémico mucho más ajustado a la realidad del paciente, para futuros desarrollos proponemos la ampliación del modelo (1) considerando factores fisiológicos del paciente como son el estado físico, la función cardiopulmonar y factores de riesgo cardiovascular que juegan un papel muy importante para mantener el bienestar del paciente [²⁴], de tal manera que el problema de control pueda ser individualizado y utilizado en pacientes con más variedad de estilos de vida.