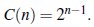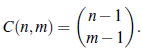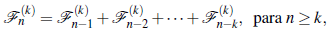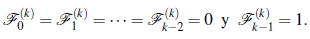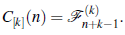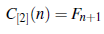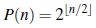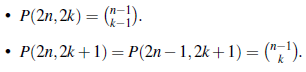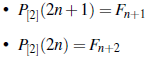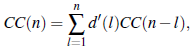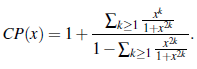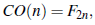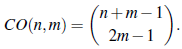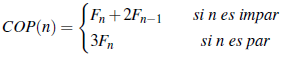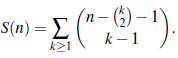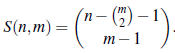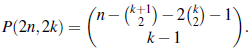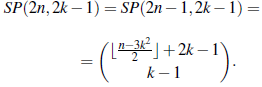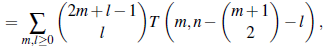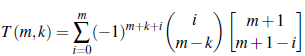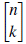1 Introducción
La composición de números enteros es un área de investigación en la combinatoria enumerativa y la teoría de números, con ella se busca establecer las formas en las que se puede representar un entero positivo como suma de enteros positivos menores o iguales a él. Aunque los orígenes de la teoría de composiciones se atribuyen a los trabajos realizados por Leonhard Euler en el siglo XVIII, la primera publicación sobre composiciones, [1] Memoir on the Theory of Compositions of a Number, fue hecha por Percy A. MacMahon en 1893. A finales de la década de 1960 aparecieron algunos artículos sobre composiciones con algunos tipos de restricciones. Pero sólo hasta este siglo se han hecho la mayoría de las publicaciones sobre composiciones, en las cuales se introducieron nuevos tipos de composiciones y métodos para determinar tales composiciones. En particular los diferentes tipos de composiciones se obtienen haciendo restricciones o generalizaciones al conjunto de las partes.
SageMath es un software matemático gratuito y de código abierto, soportado en el potente lenguaje de programación Python, para programar y realizar cálculos matemáticos complejos en distintos campos de las matemáticas a un nivel similar a los softwares de pago como Magma, Maple, Mathematica y Matlab. A través de la página web sagemath.org se puede:
trabajar en la nube (portal COCALC),
descargar la última versión para instalar en computador, o
consultar su extensa documentación.
En términos generales, el software matemático ha contribuido a la investigación en matemáticas, al proporcionar una gran cantidad de datos para hacer conjeturas; y a la enseñanza de las matemáticas, al permitir la simulación para comprender un fenómeno y proyectar la solución de problemas. Además, la ventaja de los códigos de programas hechos sobre software libre radica en que todos pueden acceder al sistema y a su comprensión, ya que todas sus implementaciones son de código abierto, a diferencia del software de pago que está orientado a un selecto grupo de investigadores y educadores que lo pueden comprar y aun así sin acceso al funcionamiento de sus rutinas.
En este artículo presentamos los códigos de los programas que hicimos en Sage para generar los diferentes tipos de composiciones, con el ánimo de contribuir con la enseñanza e investigación de esta área de las matemáticas. Particularmente, mostramos que gracias a dichos códigos se obtuvieron algunos resultados sobre composiciones superdiagonales.
2 Composiciones
Una composición de un entero positivo n es una secuencia de enteros positivos σ = [σ 1 , σ 2 ,..., σ m ] tales que σ 1 + σ 2 + ···+ σ m = n. Los σ i son llamados las partes de la composición y m es el número de partes. Por conveniencia, se define la composición vacía como la única composición de cero.
Sage incluye el comando Compositions(n) que permite obtener la lista de las composiciones del entero n.
Recuerde que en Sage para obtener ayuda sobre un comando se escribe el nombre del comando seguido por el signo de interrogación "?". Asimísmo, para ver el código interno de un comando se escribe el nombre del comando seguido por el doble signo de interrogación "??".
Ejemplo 1. Las composiciones de 5.
Denotamos por C(n) el total de composiciones del entero n. Observe en el Ejemplo 1 que C(5) = 16.
En Sage podemos utilizar el comando len(Compositions(n)) para obtener C(n).
Ejemplo 2. La secuencia C(n), para 0 ≤ n < 20.
Observe que los valores de C(n) en la anterior secuencia son siempre una potencia de dos. Este resultado fue demostrado por MacMahon usando diagramas lineales.
Teorema 3 (MacMahon [1]). El número total de composiciones de un entero positivo n es
En la literatura se conocen diversas restricciones sobre las composiciones de un entero. Por ejemplo, restringir el número de partes en la composición.
2.1 Composiciones con exactamente m partes
Las composiciones con exactamente m partes se obtienen al restringir a m el número total de partes en la composición.
En Sage podemos utilizar el comando Compositions(n, length = m) para la lista de las composiciones del entero n con m partes.
Ejemplo 4. Las composiciones de 5 con 3 partes.
Denotamos por C(n, m) el total de composiciones del entero n con exactamente m partes. Observe en el Ejemplo 4 que C( 5, 3) = 6.
El comando len(Compositions(n, length = m))
en Sage nos permite calcular C(n, m).
Ejemplo 5. La secuencia C(n, 3) con 0 < n < 20.
Con ayuda del codigo anterior podemos encontrar los primeros valores del arreglo C(n,m), n,m ≥ 1.
Observe que los valores en el arreglo anterior coinciden con el Triángulo de Pascal y con el Teorema 3 ya que la suma en cada fila es C(n) = 2n-1.
Teorema 6 (MacMahon [1]). El número total de composiciones de n con exactamente m partes es
2.2 Composiciones con partes en {1, 2,..., k}
Las composiciones del entero n con partes en el conjunto {1,2,...,k} son las composiciones de n cuyas partes son únicamente algunos de los enteros 1,2,...,k.
El comando Compositions(n,max_part=k) en Sage nos permite obtener la lista de las composiciones de n con partes en { 1 , 2, . . . , k} .
Ejemplo 7. Las composiciones de 5 con partes en {1,2,3}.
Denotamos por C [k] (n) el total de composiciones de n con partes en el conjunto { 1 , 2, . . . , k} . Observe en el Ejemplo 7 que C{12 3}(5) = 13.
El comando len(Compositions(n,max_part=k)) en Sage nos permite obtener el valor de C [k] (n).
Ejemplo 8. La secuencia C [3] (n) con 0 ≤ n < 20.
En 1975, Hoggatt y Bicknell [2], mostraron que los valores de la secuencia C [k] (n) tienen una correspondencia con los números k-generalizados de Fibonacci (o números k-bonacci).
Los números k-bonacci se definen recursivamente como
con valores iniciales,
Por ejemplo, la secuencia de números Tribonacci es (OEIS-A000073)1:
0,0,1,1,2,4,7,13,24,44,81,149,274,...
Observe en el Ejemplo 8 que los valores de la secuencia C [3] (n) corresponden con los números Tribonacci con n ≥ 2. Esto es cierto en general.
Teorema 9 (Hoggatt y Bicknell [2]). El número total de composiciones de n con partes en el conjunto {1,2,...,k} es
Corolario 10. El número total de composiciones de n con partes en el conjunto { 1 , 2} es
donde F n+1 es el número de Fibonacci n+ 1.
3 Composiciones palíndromas
Las composiciones palíndromas de un entero n son aquellas composiciones de n en las que las partes se leen de la misma forma de izquierda a derecha que de derecha a izquierda. Denotaremos por P(n) el total de composiciones palíndromas de n.
La tabla 1 muestra el código del programa en Sage para obtener las composiciones palíndromas de un entero positivo n.
Ejemplo 11. Las composiciones palíndromas de 6. sage: Palin(6)
La secuencia P(n) con 0 ≤ n< 20.
La propiedad observada en el Ejemplo 11 para la secuencia P(n), fue demostrada por Hoggatt y Bicknell utilizando diagramas de barras.
Teorema 12 (Hoggatt y Bicknell [2]). El número total de composiciones palíndromas de n es
donde [·] es la usual función parte entera.
3.1 Composiciones palíndromas con m partes
Denotamos por P( n, m) el total de composiciones palíndromas con exactamente m partes.
La Tabla 2 muestra el código del programa en Sage para obtener las composiciones palíndromas de n con exactamente m partes.
Ejemplo 13. Las composiciones palíndromas de 21 con 3 partes.
La secuencia P(n, 3) para 0 ≤ n < 20.
En [2] Hoggatt y Bicknell también mostraron que el total de composiciones palíndromas de n con m partes depende de la paridad del número de partes. Note que no hay composiciones palíndromas de un número impar con un número par de partes.
Teorema 14 (Hoggatt y Bicknell, [2]). El total de composiciones palíndromas de n con m partes es
3.2 Composiciones palíndromas con partes en el conjunto {1,2}
Denotamos por P [2] ( n) el total de composiciones palíndromas con partes en {1,2}.
La Tabla 3 muestra el código del programa en Sage para obtener las composiciones palíndromas con partes en { 1 , 2} .
Ejemplo 15. Las composiciones palíndromas de 6 con partes en { 1 , 2} .
La secuencia P [2] (n) con 0 ≤ n < 20.
En [3] Alladi y Hoggatt mostraron que existe una correspondencia de las composiciones palíndromas con partes en { 1 , 2} y los números de Fibonacci.
Teorema 16 (Alladi y Hoggatt [3]). El número total de composiciones palíndromas de un entero n con partes en el conjunto { 1 , 2} es
donde F n+1 y F n+2 son los números de Fibonacci n + 1 yn + 2, respectivamente.
4 Composiciones de Carlitz
Las composiciones de Carlitz de un entero n son las composiciones de n sin partes adyacentes iguales. Denotamos por CC(n) el total de composiciones de Carlitz de n.
La Tabla 4 muestra el código del programa en Sage para obtener las composiciones de Carlitz de n.
Ejemplo 17. Las composiciones de Carlitz de 6.
La secuencia CC(n) con 0 ≤ n < 20.
En [4] Carlitz presentó una formula recursiva para CC(n) en función de la diferencia del número de divisores pares e impares de los enteros no negativos menores o iguales a n.
Teorema 18 (Carlitz [4]). El total de composiciones de Carlitz de n es
donde d'(n) denota la diferencia entre el número de divisores impares y pares de n.
4.1 Composiciones de Carlitz palíndromas
Denotamos por CP(n) el total de composiciones de Carlitz palíndromas del entero n.
La Tabla 5 muestra el código del programa en Sage para obtener las composiciones de Carlitz palíndromas de n.
Ejemplo 19. Las composiciones de Carlitz palíndromas de 7.
La secuencia CP(n), para 0 ≤ n < 20.
La secuencia de CP(n) es (OEIS-A239327): 1,1,1,1,2,3,2,5,5,7,10,14,14,25,26,42,48, . . .
El siguiente teorema, demostrado por Carlitz en [4], establece la función generatriz CP(x) = Σ n≥0 CP(n)x n . Que puede utilizarse para determinar los valores de la secuencia CP(n).
Teorema 20 (Carlitz [4]). La función generatriz para el número de composiciones de Carlitz palíndroma es
5 Composiciones coloreadas
Las siguientes composiciones, a diferencia de las anteriores, representan una generalización de las composiciones clásicas al permitir que cada parte de la composición se pueda colorear.
Las composiciones coloreadas de un entero n son son las composición de n en la que cada parte de tamaño i se puede colorear en i diferentes colores. Usualmente se utilizan subíndices i 1 , i 2 , . . . , i i para indicar las coloraciones de una parte de tamaño i.
Denotaremos por CO(n) el número total de composiciones coloreadas de n.
La tabla 6 muestra el código del programa en Sage para obtener las composiciones coloreadas de n. Este programa imprime las coloraciones de cada parte de tamaño i como i_1 , i_2 , . . . , i_i .
Ejemplo 21. Las composiciones coloreadas de 4.
La secuencia CO(n) con 0 ≤ n < 20.
En [5] Agarwal introduce y demuestra que el total de composiciones de n en términos de los números pares de Fibonacci.
Teorema 22 (Agarwal [5]). El número total de composiciones coloreadas de n es
donde F 2n es el número de Fibonacci 2n.
5.1 Composiciones coloreadas con m partes
Denotaremos por CO(n, m) para indicar el total de composiciones coloreadas de un entero n con exactamente m partes.
La tabla 7 muestra el código del programa en Sage para obtener las composiciones coloreadas con exactamente m partes.
Ejemplo 23. Las composiciones coloreadas de 4 con 3 partes.
La secuencia CO(n, 3) con 0 ≤ n < 20.
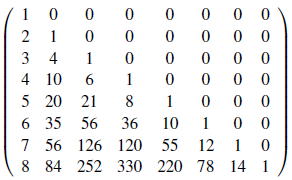
Con ayuda del código del programa de la tabla 7 podemos encontrar los primeros valores del arreglo CO(n,m), n,m ≥ 1.
En [5] Agarwal también presenta y demuestra la formula para obtener CO(n, m).
Teorema 24 (Agarwal [5]). El número total de las composiciones coloreadas de n con m partes es
5.2 Composiciones coloreadas palíndromas
Denotaremos por COP(n) para indicar el total de composiciones coloreadas palíndromas de n.
La tabla 8 muestra el código del programa en Sage para obtener las composiciones coloreadas palíndromas de un entero positivo n.
Ejemplo 25. Las composiciones coloreadas palíndromas de 4.
La secuencia COP(n) con 0 ≤ n < 20.
En [5] Agarwal demuestra el siguiente teorema que establece la formula para obtener COP(n) en términos de los números de Fibonacci y que depende de la paridad del entero positivo n.
Teorema 26 (Agarwal [5]). El número total de las composiciones coloreadas palíndromas de un entero positivo n es
donde F n y F n-1 son los números de Fibonacci n y n -1, respectivamente.
Las siguientes composiciones fueron introducidas por Deutsch, Munarini y Rinaldi en [6].
6 Composiciones superdiagonales
Las composiciones superdiagonales del entero n son las composiciones de n en las que cada parte es mayor o igual que la posición de la parte. Es decir, son las composiciones σ = [σ 1 , σ 2,..., σ k] de n tales que σ l ≥ l para todo 1 ≤ l ≤ k.
Denotaremos por S(n) para indicar el número total de composiciones superdiagonales de n.
La tabla 9 muestra el código del programa en Sage para obtener las composiciones superdiagonales.
Ejemplo 27. Las composiciones superdiagonales de 7.
La secuencia S(n) con 0 ≤ n < 20.
En [6] Deutsch, Munarini y Rinaldi dan la formula para obtener el número de composiciones superdiagonales de un entero positivo n.
Teorema 28 (Deutsch et al. [6]). El número total de composiciones superdiagonales de n es
6.1 Composiciones superdiagonales de n con m partes
Denotaremos por S(n, m) para indicar el total de composiciones superdiagonales de n con m partes.
La tabla 10 muestra el código del programa en Sage para obtener las composiciones superdiagonales de n con m partes.
Ejemplo 29. Las composiciones superdiagonales de 9 con 3 partes.
La secuencia S(n, 2) para 0 ≤ n < 20.
La secuencia S(n, 3) para 0 ≤ n < 20.
En [6] se demuestra la formula para obtener el total de composiciones superdiagonales de n con exactamente m partes.
Teorema 30 (Deutsch et al. [6]). El número total de composiciones superdiagonales de n con m partes es
6.2 Composiciones superdiagonales palíndromas
Denotaremos por SP(n) para indicar el total de composiciones superdiagonales palíndromas de n.
La tabla 11 muestra el código del programa en Sage para obtener las composiciones superdiagonales palíndromas.
Ejemplo 31. Las composiciones superdiagonales palíndromas de 15.
La secuencia SP(n) con 0 ≤ n < 20.
Denotaremos por SP(n, m) para indicar el total de composiciones superdiagonales palíndromas de n con m partes.
La tabla 12 muestra el código del programa en Sage para obtener las composiciones superdiagonales palíndromas de n con m partes.
Ejemplo 32. Las composiciones superdiagonales palíndromas de 17 con 3 partes.
La secuencia SP(n, m) con 0 ≤ n < 20 y m = 2, 3.
La secuencia SP(n, 5) con 20 ≤ n < 40.
Observe en el Ejemplo 32 que el número total de composiciones superdiagonales palíndromas de n con m partes depende de la paridad del número de partes. Además, note que no hay composiciones superdiagonales palíndromas de un número impar con un número par de partes.
Teorema 33 (M., O-L y Ramírez [7]).
1. El total de las composiciones palíndromas de un entero par con un número par de partes es
2. El total de las composiciones palíndromas de un entero par o impar con un número impar de partes es
6.3 Composiciones superdiagonales coloreadas
Denotamos por SCO(n) para indicar el total de composiciones superdiagonales coloreadas de n.
La tabla 13 muestra el código del programa en Sage para obtener las composiciones superdiagonales coloreadas.
Ejemplo 34. Las composiciones superdiagonales coloreadas de 4.
La secuencia SCO(n) con 0 ≤ n< 20.
Teorema 35 (M., O-L y Ramírez [7]). El total de composiciones superdiagonales coloreadas de n es SCO(n)=
donde
6.4 Composiciones superdiagonales de Carlitz
Denotaremos por SC(n) para indicar el total de composiciones superdiagonales de Carlitz de n.
La tabla 14 muestra el código del programa en Sage para obtener las composiciones superdiagonales de Carlitz para un entero positivo n.
Ejemplo 36. Las composiciones superdiagonales de Carlitz de 7.
La secuencia SC(n) con 0 ≤ n < 20.
Problema abierto: encontrar una fórmula para el total de composiciones superdiagonales de Carlitz de un entero positivo n.
7 Conclusiones
Presentamos los códigos de los programas hechos en SageMath para generar las distintas restricciones y generalizaciones de la composiciones más citadas en la literatura. Esperamos que sirvan de soporte al estudio, investigación y enseñanza de la teoría de composiciones, rama de investigación activa en Combinatoria y Teoría de Números.
La ventaja de SageMath está en su gratuidad, a diferencia del software de pago que esta orientado al selecto grupo de investigadores y profesores de matemáticas que lo pueden comprar. Iniciativa que ayuda a contribuir a la apertura de la ciencia para beneficio de toda la sociedad.
Hemos incluido los códigos presentados en este artículo en el repositorio Noesis de la Universidad Industrial de Santander. https://noesis.uis.edu.co/handle/20.500.14071/4523