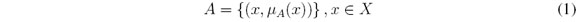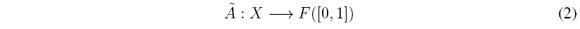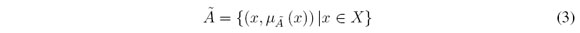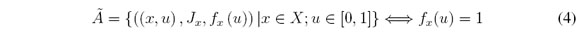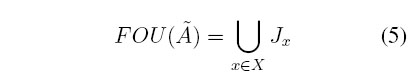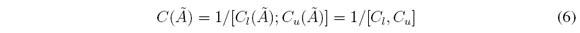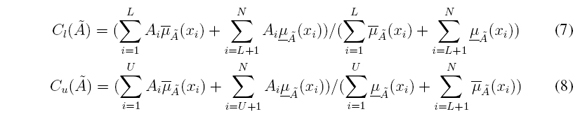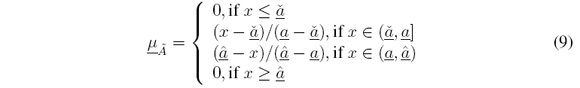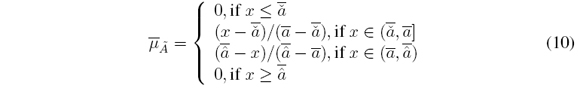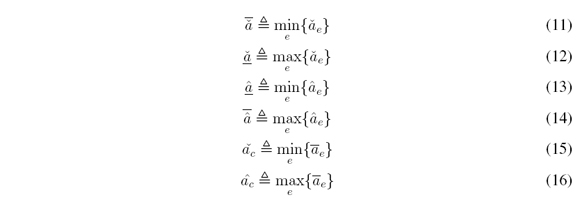Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería
versão impressa ISSN 0121-750X
ing. vol.21 no.2 Bogotá ago. 2016
https://doi.org/10.14483/udistrital.jour.reving.2016.2.a01
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.2.a01
Metodología para el Diseño de Conjuntos Difusos Tipo-2 a partir de Opiniones de Expertos
Methodology for Designing Type-2 Fuzzy sets from Experts Opinions
Mónica Rodríguez
Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. moniklra 132@hotmail.com
Yeniffer Huertas
Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. yeniffer-21@hotmail.com
Recibido: 08-10-2015. Modificado: 27-01-2016. Aceptado: 10-02-2016
Resumen
Contexto: Existe una creciente necesidad de procesar la información proveniente del lenguaje humano, la cual incluye incertidumbre, con el fin solucionar problemas definidos en un determinado contexto.
Método: Empleamos conjuntos difusos Tipo-2 a fin de representar y cuantificar el lenguaje humano, para lo cual presentamos una serie de aspectos metodológicos para su diseño. La propuesta se compone de tres actividades clave: (1) determinar la etiqueta lingüística(palabra), (2) definir su función de pertenencia y (3) recolectar la información desde los expertos.
Resultados: Se aplica y valida la propuesta en un escenario real basado en conjuntos triangulares a través de la comparación de dos grupos de expertos. Se modela, procesa y analiza la información de entrada permitiendo hacer un manejo adecuado a la incertidumbre implícita en sus opiniones.
Conclusiones: La metodología propuesta es aplicable a diferentes situaciones, donde múltiples sujetos expresan su opinión o percepción que manifiestan al rededor de determinado problema.
Palabras clave: conjuntos difusos Tipo-2, incertidumbre, percepción,información, lenguaje.
Lenguaje: español.
Abstract
Context: There is a need for processing information coming from human like language that includes uncertainty in order to solve problems defined in that context.
Method: We use Type-2 fuzzy sets for defining and measuring human like language, so we propose a methodology for designing them. The proposal is composed by three key steps:(1) defining a linguistic label (word), (2) defining its membership function, and (3) collecting information from experts.
Results: The proposal is applied and validated in a real scenario based on triangular fuzzy sets through two different groups of experts. We present a proposal to model, process and analyze input information coming from experts that allows to do an appropriate handling of uncertainty present in people perceptions.
Conclusions: The proposed methodology is applicable to different problems where different people express their opinions and/or perceptions about a specific problem.
Keywords: uncertainty, perception, information, language, Type-2 fuzzy sets.
1. Introducción
El ser humano se enfrenta a diario a situaciones que involucran incertidumbre asociada a información ambigua e imprecisa, por lo que emplea el lenguaje natural de su elección para comunicar opiniones o juicios relacionados a una situación particular. A pesar de que la raza humana puede hablar más de 6000 lenguas diferentes [1], siempre existe un medio de comunicación el cual dos o más individuos utilizan un mismo lenguaje para comunicarse. La información transmitida a través de dicho lenguaje no se puede representar directamente con valores numéricos exactos, lo que genera un grado de incertidumbre que surge de la percepción de cada individuo frente al tema tratado y del significado que tienen las palabras que usa para explicarlo.
En la descripción real de un problema generalmente se recurre a expertos que proporcionan datos cuya precisión numérica puede ser demasiado costosa e insustancial, dado que el pensamiento humano no trabaja de esa manera [2]. A partir de este supuesto nace la necesidad de dar respuesta a esta situación en términos numéricos, pero de una manera más natural a cada caso, a través de descripciones lingüísticas que tienen connotaciones difusas en las que frecuentemente no es clarificado donde comienza y finaliza su significado.
Con el propósito de analizar todas las percepciones de un grupo de expertos (inter-incertidumbre) se emplean conjuntos difusos Tipo-2 (IT2 FSs), dado que modelan la imprecisión inmersa en el lenguaje emitido por cada uno de ellos [3] y ofrecen una solución capaz de manejar la incertidumbre que propende al riesgo. La información de entrada que proporciona el conjunto de expertos debe tener unas características especiales que se establecen a la hora de la recolección, seguida de un proceso de ordenamiento que lleva finalmente a la computación perceptual.
Así pues, aunque el problema de construcción de funciones de pertenencia que capturen adecuadamente los significados de las descripciones lingüísticas ya ha sido abordado por varios autores [3], [4], se considera necesario profundizar en el proceso de recolección de la información de entrada detallando los pasos para la construcción del conjunto difuso.
Los conjuntos difusos Tipo-2 han tenido exitosas aplicaciones en diferentes escenarios, como el diagnóstico médico [5], selección de personal [6], evaluación de desempeño [7],[8], confort térmico [9], toma de decisiones [10] y otros [11]-[13]. En dichas aplicaciones se propone una metodología que detalla el procedimiento a seguir para el diseño de conjuntos difusos con función de pertenencia triangular, partiendo de la recolección de información de entrada hasta llegar a la construcción e interpretación mediante el análisis estadístico del mismo.
A continuación se presentan conceptos básicos acerca de conjuntos difusos Tipo-1 y Tipo-2 así como diferentes medidas que nos proporcionan información sobre el comportamiento del problema; seguido de la descripción de la metodología propuesta basada en una encuesta, el tratamiento estadístico de la información obtenida y el análisis de dichos resultados para la construcción de la función de pertenencia asociada, se expone una aplicación de la metodología a un caso real basado en conjuntos triangulares de manera que se pueda analizar y validar, para finalizar con algunas conclusiones del trabajo.
2. Conjuntos difusos
La teoría de conjuntos difusos surge de la necesidad de tratar y procesar información afectada por la incertidumbre no probabilística del entorno. El término es introducido por Lofti A. Zadeh [14] en 1965 y se utiliza para representar matemáticamente la imprecisión o ambigüedad inmersa en distintos campos de la vida cotidiana, proporcionando herramientas para manejarla.
El modelamiento de la realidad de manera estática genera pérdida de información importante en el análisis de muchos problemas, debido a las opiniones y juicios vagos e imprecisos generados por el lenguaje natural utilizado por las personas que se involucran en el problema, así como sus relaciones. Los conjuntos difusos permiten describir y caracterizar la realidad usando modelos flexibles que proceden de descripciones lingüísticas a través de funciones de pertenencia. Un conjunto difuso A es definido como un par ordenado [15]:
donde μA(x) es el grado de pertenencia de x en A y μA es la función de pertenencia asociada a la palabra A, que define el grado en el cual cada elemento del universo de discurso X pertenece al conjunto difuso. El universo de discurso x Є X es un conjunto clásico que toma valores en ℝ.
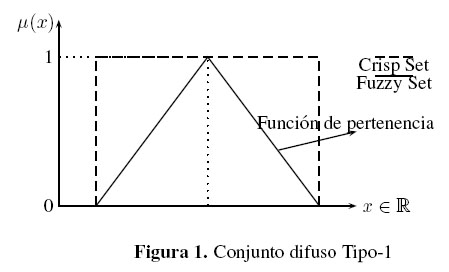
En conjuntos difusos de este tipo cada elemento del conjunto tiene un grado de pertenencia asociado, representado por un número en el intervalo unitario [0; 1] y son llamados conjuntos difusos clásicos o conjuntos difusos Tipo-1. Sus funciones de pertenencia son precisas y requieren que a cada elemento del universo de discurso le sea asignado un número real particular.
En la figura 1 se representa un conjunto difuso donde en el eje de abscisas se indican los elementos del conjunto universo X y en el de las ordenadas los grados de pertenencia, definiendo así la función de pertenencia μ(x). De la misma manera se realiza el contraste con un conjunto clásico donde la pertenencia es total.
3. Conjuntos difusos Tipo-2 de intervalo
En algunos contextos es posible identificar fuentes de incertidumbre asociadas al lenguaje natural, donde se puede ponderar dicha incertidumbre con grados de pertenencia a su vez difusos, considerándolos de esta manera como incertidumbre difusa Tipo-2. En general, un conjunto difuso Tipo-2 es una generalización de un conjunto difuso en cuanto se asocia una fuente secundaria de incertidumbre relacionada con la definición de una palabra o conjunto A. Dicha fuente adicional de incertidumbre se representa como una función de pertenencia secundaria asociada a cada valor de x Є X (o universo de discurso),en otras palabras:
donde F([0; 1]) es el conjunto de todos los conjuntos difusos Tipo-1 que pueden ser definidos dentro del universo de discurso x Є X.
Los conjuntos difusos Tipo-2, cuya función de pertenencia secundaria es un intervalo(es decir que la incertidumbre asociada al lenguaje es tratada de manera equitativa), son llamados conjuntos difusos de intervalo o IT2FSs (por sus siglas en inglés) [4] o también conjuntos difusos Tipo-2 de intervalo (IT2FSs), ya que los grados de pertenencia asignados a los elementos del universo de discurso son un intervalo.
Lofti A. Zadeh [14] explica que un IT2FS es expresado por dos funciones de pertenencia, donde una representa el grado de pertenencia en X y la otra da una ponderación a cada uno de los conjuntos difusos Tipo-1. Así, un IT2FS es definido como:
Por otra parte, el conjunto difuso primario Jx está ponderado por el conjunto difuso fxμ como una función de pertenencia secundaria:
donde x es la variable primaria, Jx es un intervalo [0; 1] que representa la pertenencia primaria de x, μ es la variable secundaria y fxμ es la función de pertenencia secundaria de x.
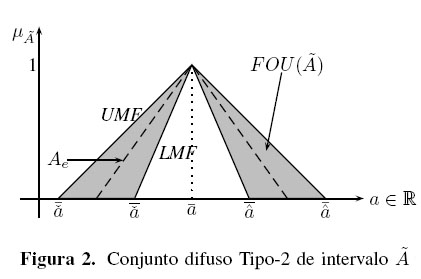
La Huella de Incertidumbre (FOU, Footprint of Uncertainty, por sus siglas en inglés) de los conjuntos difusos Tipo-2 [17] define la incertidumbre de 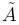 como la unión de todas las pertenencias primarias,
como la unión de todas las pertenencias primarias,
la cual está limitada por dos funciones de pertenencia: una función de pertenencia superior (UMF, Upper membership function, por sus siglas en ingle's) 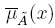 y una función de pertenencia inferior (LMF, Lower membership function, por sus siglas en inglés)
y una función de pertenencia inferior (LMF, Lower membership function, por sus siglas en inglés) 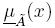 donde son conjuntos difusos Tipo-1 y tienen e conjuntos empotrados
donde son conjuntos difusos Tipo-1 y tienen e conjuntos empotrados 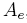 ; en consecuencia el grado de pertenencia de cada elemento de un IT2FS es un intervalo
; en consecuencia el grado de pertenencia de cada elemento de un IT2FS es un intervalo 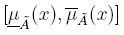 [18].
[18].
El conjunto tiene un valor esperado obtenido mediante una reducción de tipo [19] que nos proporciona información acerca del posible comportamiento del problema. Dicha medida es el centroide que corresponde a un intervalo cerrado formado por todos lo centroides de los conjuntos difusos Tipo-1 empotrados contenidos en la huella de incertidumbre (FOU) de 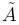 [20],
[20],
donde 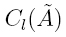 y
y 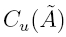 son la cota inferior y superior del centroide. Los conjuntos difusos Tipo-2 de intervalo tienen una cantidad infinita de centroides incrustados en su FOU, siendo su cálculo un proceso iterativo donde las ecuaciones generales para el cálculo de las cotas son:
son la cota inferior y superior del centroide. Los conjuntos difusos Tipo-2 de intervalo tienen una cantidad infinita de centroides incrustados en su FOU, siendo su cálculo un proceso iterativo donde las ecuaciones generales para el cálculo de las cotas son:
donde 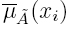 y
y 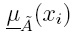 son los valores superior e inferior de la función de pertenencia, L el punto que marca el cambio de
son los valores superior e inferior de la función de pertenencia, L el punto que marca el cambio de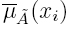 a
a 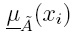 y R el punto que marca el cambio de
y R el punto que marca el cambio de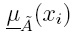 a
a 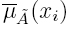 .
.
4. Metodología propuesta para la obtención de conjuntos difusos Tipo-2
Las descripciones lingüísticas asociadas al juicio de los expertos acerca de una situación particular contienen incertidumbre donde no se presenta claramente el inicio y el fin del significado, por lo cual es necesario identificar la manera de diseñar IT2FSs, con el propósito de manejar este tipo de información. La metodología propuesta no requiere sujetos con conocimiento sobre conjuntos difusos, permite recolectar información de un grupo de expertos y tener en cuenta todas las percepciones que componen la huella de incertidumbre (FOU). El enfoque propuesto se basa en tres pasos:
- Determinar la palabra que se desea representar.
- Definir la función de pertenencia que se desea obtener.
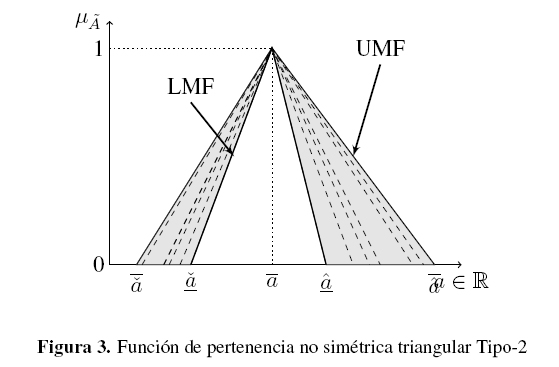
La figura 3 muestra una FOU sencilla donde las funciones de pertenencia inferior (LMF) y superior (UMF) son triangulares. Esta es la función esperada en el desarrollo del enfoque propuesto. La función de pertenencia inferior se define como sigue:
La función de pertenencia superior se define como sigue:
Es importante tener en cuenta que para obtener una función de pertenencia como la mostrada en la figura 3, debe asignarse un valor esperado, porque si este valor queda a discreción de los múltiples expertos, se obtendrían muchos valores diferentes que seguramente modificarían su forma.
Luego de la selección, viene el diseño del método para la recolección de información, que permitirá obtener una función de pertenencia triangular.
3. Utilizar la percepción de múltiples expertos en la recolección de información. El procedimiento a seguir para alcanzar el objetivo se compone de tres actividades principales: (1) Llevar a cabo una encuesta, (2) Tratamiento estadístico de la información y (3) Análisis de resultados.
4.1. La encuesta
El enfoque desarrollado tiene como fin obtener la información esperada, entendiéndola como el resultado de un correcto entendimiento de lo que se requiere, para lo que se propone llevar a cabo una encuesta que capture la opinión de un experto acerca de una variable específica.
Es necesario que el contenido del material utilizado para la recolección de información sea lo suficientemente claro para cualquier sujeto, considerando que la metodología se diseña para ser aplicada a personas que no conocen la teoría de conjuntos difusos. El cuestionario debe incluir:
- Un encabezado: que permite al experto encuestado comprender qué información es la que debe proveer para asegurar el éxito de la encuesta. El objetivo es obtener valores numéricos sencillos que representen la percepción que una persona tiene acerca de la palabra.
- Preguntas sencillas y eficientes: se le pide al encuestado que proporcione su percepción sobre los parámetros requeridos, previamente definidos por la función de pertenencia que se quiere obtener, descrita en un universo de discurso establecido. Los expertos deben ubicar los puntos límite del intervalo que individualmente asocian con la palabra dentro de un rango, de acuerdo con tres escenarios: el primero representa una opinión optimista, el segundo el valor esperado y el tercero la posición pesimista. Es importante considerar que la información obtenida como resultado de la encuesta debe ser computable.
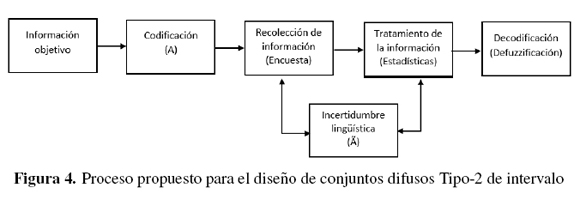
La figura 4 representa la metodología propuesta como un proceso cuya entrada de información es codificada, seguida de una transformación que parte de la recolección de información a través de la encuesta, generando resultados que poseen incertidumbre lingüística; y finalmente una salida en la cual la información es defuzzificada mediante el tratamiento estadístico.
4.2. Tratamiento estadístico
Según Mendel [3] cada sujeto proporciona los puntos límite de un intervalo asociado con una palabra sobre una escala predeterminada. La figura 3 muestra como el IT2Fs es descrito completamente por la FOU, la cual es expresada por la unión de las opiniones de expertos representadas por conjuntos difusos Tipo-1 empotrados 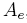 .
.
Para realizar el tratamiento estadístico de los datos es necesario determinar los puntos límite del intervalo en el universo discurso X, usando los operadores máximos y mínimos que conforman la función de pertenencia superior (UMF) y la función de pertenencia inferior (LMF). Se procede a determinar los parámetros dados por las siguientes ecuaciones:
4.2.1. Tamaño muestral
Dado que los procesos de inferencia difusa no pretenden hacer inferencia estadística desde un punto de vista probabilístico, no se plantea la necesidad de contar con tamaños de muestras adecuados para inferir la población de interés. Por otra parte, los sistemas difusos no buscan generalizar medidas probabilísticas en el sentido amplio de la palabra, sino representar incertidumbre de tipo lingüístico utilizando la información disponible, lo cual corresponde a un muestreo de conveniencia o por selección intencionada.
Recomendamos entonces el uso de la totalidad de los expertos pertinentes disponibles. En casos donde exista posibilidad de realizar muestreos con el fin de reducir la cantidad de encuestas a realizar, podría esto complementar los resultados obtenidos. Sin embargo y como en muchas aplicaciones prácticas se observa, únicamente se puede trabajar con una cantidad de información limitada por diferentes factores como disponibilidad de expertos, costos asociados a las encuestas, pertinencia y grado de experticia de las personas encuestadas, etc. por lo que no siempre es factible aplicar técnicas de muestreo probabilístico.
4.3. Análisis de resultados
Un análisis descriptivo del comportamiento de la variable en cuestión (la palabra definida inicialmente) es presentado y seguido a este, los conjuntos obtenidos de diferentes grupos de expertos son comparados, identificando el tamaño de la variación entre los mismos. Así pues, se utilizan las ecuaciones 11 - 16 con el fin de parametrizar completamente la palabra que es objeto de pregunta a los expertos. Algunas medidas de interés que se pueden computar a través de lo obtenido son:
- Centroide (valor esperado)
- Varianza (dispersión)
- Ordenamiento entre palabras (orden)
Dichas medidas se utilizan dado que la teoría existente acerca de medidas de incertidumbre sobre conjuntos difusos Tipo-2 están aún en desarrollo [11], [18], [21]. Otras medidas de desempeño podrán ser utilizadas en el futuro, a medida que la teoría de conjuntos difusos Tipo-2 avance.
5. Ejemplo de aplicación
La metodología presentada es de carácter general y puede ser utilizada para obtener diferentes tipos de conjuntos difusos, dependiendo de las necesidades del usuario. A continuación presentamos un ejemplo obtenido de información real de cómo obtener conjuntos difusos triangulares, y aun cuando existe una amplia gama de conjuntos difusos que se pueden obtener mediante la metodología propuesta, no es el objetivo general de este artículo el ejemplificar dicha gama de conjuntos difusos sino la de aplicarla a una situación real.
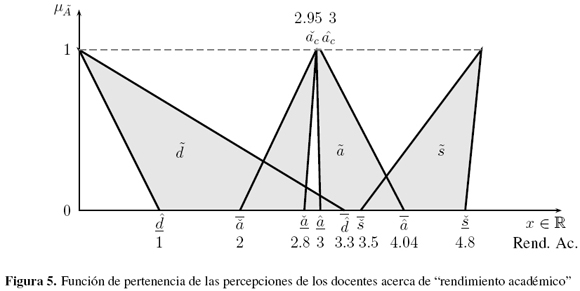
5.1. Percepciones de los docentes acerca de "rendimiento académico"
La siguiente aplicación está basada en la percepción de veinticinco docentes de último semestre de ingeniería industrial de una universidad pública acerca de la expresión "rendimiento académico". Cabe anotar que se usaron las encuestas que fueron respondidas, ya que aunque se envió la encuesta a toda la población de docentes de último semestre de ingeniería industrial de dicha universidad, no todos la contestaron, por tanto se utilizó la información disponible. Los docentes contestaron una encuesta la cual incluye las siguientes preguntas relacionadas con las notas numéricas asociadas con un rendimiento académico deficiente, aceptable y sobresaliente:
- Sabemos que cero (0) corresponde a un rendimiento académico deficiente. ¿Hasta qué calificación considera que un estudiante continúa con un rendimiento académico deficiente?
- Sabemos que cinco (5) corresponde a un rendimiento académico sobresaliente. ¿Desde qué calificación considera que un estudiante comienza a tener un rendimiento académico sobresaliente?
- Para que un estudiante apruebe una asignatura debe obtener una calificación de 2.95, siendo esta asociada con un rendimiento académico aceptable. ¿En qué rango considera que un estudiante mantiene un rendimiento académico aceptable? (Note que un rendimiento aceptable no implica que se apruebe o no una asignatura en particular, ya que el estudiante puede obtener una nota menor o mayor al valor al requerido por diferentes externalidades que interfieren con su desempeño).
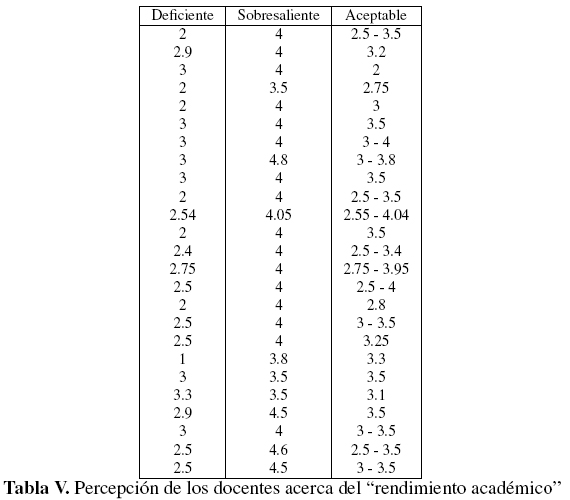
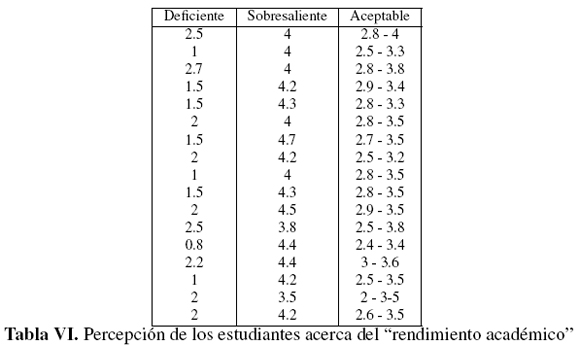
La tabla V muestra las respuestas obtenidas en la encuesta (ver apéndice).
Después de realizar el tratamiento estadístico de las respuestas, los intervalos de puntos finales son determinados en el conjunto difuso asociado con cada uno de los rendimientos académicos, obteniendo los parámetros: 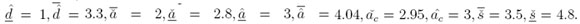 La tabla I muestra los centroides y sus varianzas para las percepciones de los docentes asociadas con cada uno de los rendimientos académicos considerados: En este caso, cuando analizamos los centroides (tabla I) para obtener información acerca del comportamiento del problema, se observa lo siguiente: 0.29 ≤ 3.41; 1.18 ≤ 2.61; 2.61 ≤ 4.7 y 3.41 ≤ 4.18.
La tabla I muestra los centroides y sus varianzas para las percepciones de los docentes asociadas con cada uno de los rendimientos académicos considerados: En este caso, cuando analizamos los centroides (tabla I) para obtener información acerca del comportamiento del problema, se observa lo siguiente: 0.29 ≤ 3.41; 1.18 ≤ 2.61; 2.61 ≤ 4.7 y 3.41 ≤ 4.18.
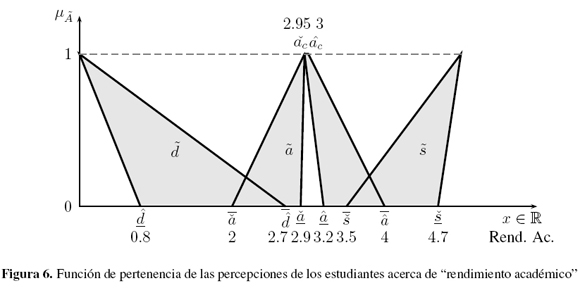
5.2. Percepción de los estudiantes acerca de "rendimiento académico"
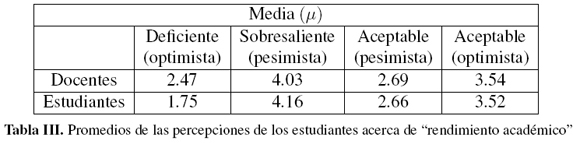
En la misma forma, la encuesta fue realizada a un grupo de diecisiete estudiantes de último semestre de ingeniería industrial de una universidad pública para determinar su percepción acerca de rendimiento académico. Los resultados obtenidos se muestran en la Tabla VI (Apéndice). La figura 6 representa la percepción de los estudiantes acerca de "rendimiento académico". Al realizar el tratamiento estadístico de las respuestas, los intervalos de puntos finales son determinados en los conjuntos difusos asociados con cada uno de los rendimientos académicos, obteniendo los parámetros: 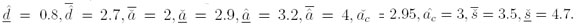
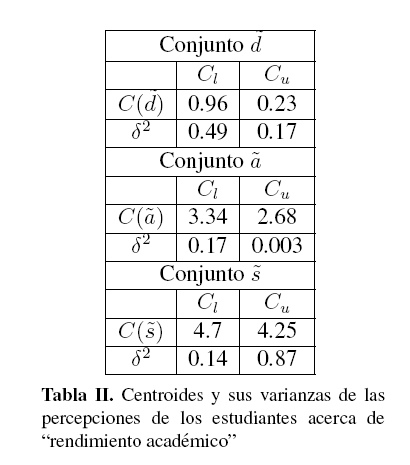
La tabla II muestra los centroides y sus varianzas para las percepciones de los estudiantes asociadas con cada uno de los rendimientos académicos considerados: En este caso, cuando analizamos los centroides (tabla II) para obtener información acerca del comportamiento del problema, se observa lo siguiente: 0.23 ≤ 3.34; 0.96 ≤ 2.68; 2.68 ≤ 4.7 y 3.34 ≤ 4.25
5.3. Análisis de los resultados de la aplicación
Basados en los resultados se puede observar la similitud en la percepción de rendimiento académico aceptable y sobresaliente para estudiantes y docentes, pero una diferencia significativa en la percepción de rendimiento académico deficiente, lo que nos indica que el intervalo asociado a la etiqueta lingüística según el juicio de los docentes es exigente.
De acuerdo con [21] se puede afirmar que efectivamente se usa el orden parcial de intervalos de los centroides en ambos cumpliendo con lo siguiente:
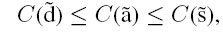 lo cual implica que
lo cual implica que 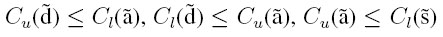 y
y 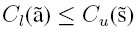
Entonces, el orden de las palabras en ambos casos es el siguiente:
deficiente ≤ aceptable ≤ sobresaliente
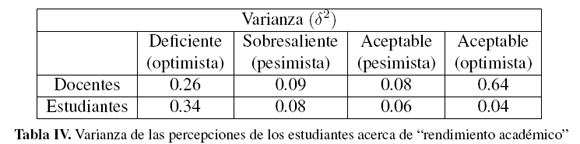
En un análisis descriptivo de la varianza de las percepciones se puede observar que hay una mayor dispersión en la opinión respecto al rendimiento académico deficiente (optimista) con δ2 = 0.26 en la percepción de los docentes (tabla IV) y δ2 = 0.34 en la percepción de los estudiantes (tabla IV). De igual forma la variabilidad es considerable en la percepción del rendimiento académico sobresaliente (pesimista) para los docentes con δ 2= 0.64 (tabla IV)
El análisis realizado con las medidas de interés descritas y calculadas anteriormente como lo son el centroide, la varianza y el ordenamiento de palabras, nos permiten concluir que las opiniones de los dos grupos de expertos son similares, contrario a lo que se podría pensar, dado que estos se encuentran en condiciones muy diferentes.
6. Conclusiones
Se propone una metodología sencilla de implementar para obtener información de expertos con el fin de diseñar conjuntos difusos Tipo-2 con función de pertenencia triangular. Nuestra propuesta es una alternativa que ayuda a las personas a comprender la incertidumbre asociada al lenguaje, la cual es aplicable a diferentes campos a través del diseño de una encuesta.
El caso de estudio permite observar cómo la metodología propuesta provee una alternativa sencilla y muy útil para el diseño de IT2FSs triangulares asimétricos a través de información procedente de una encuesta aplicada a dos grupos de expertos. Su aplicabilidad en diferentes situaciones, donde múltiples expertos tienen diferentes percepciones y comprensiones de un mismo problema, es alta y ofrece una alternativa para el tratamiento de información que proviene de conceptos y palabras, pero no de números y cuantificaciones clásicas.
Es interesante comparar las respuestas de diferentes grupos de personas con diferentes características, pero percepciones similares. El diseño de un conjunto difuso Tipo-2 de intervalo nos permite modelar la incertidumbre generada en el lenguaje natural que elige emplear el ser humano para expresar sus opiniones sobre una variable. A través de la metodología presentada se asegura que la información de entrada permita ser procesada, tratada y analizada de forma adecuada, con el fin de facilitar un posterior proceso de toma de decisiones.
Para finalizar, es importante tener en cuenta que diversos factores pueden afectar la confiabilidad de la metodología propuesta, tales como el nivel verdadero de experticia de las personas encuestadas, la disponibilidad de personas a encuestar y la complejidad de los conjuntos difusos que se pretenden parametrizar. Recomendamos realizar preguntas sencillas y fáciles de entender con el fin de no agregar incertidumbre adicional el análisis.
Trabajo futuro
En futuros trabajos se pretende experimentar con varios tipos de funciones de pertenencia para validar la generalidad de la metodología. Recalcamos la importancia del proceso de formulación de las preguntas de la encuesta, ya que de ellas depende la forma de la función de pertenencia que se obtendrá.
Referencias
[1] S. R. Anderson, "How many languages are there in the world?." , disponible en http://www.linguisticsociety.org/content/how-many-languages-are-there-world, 2010. [ Links ]
[2] Y. Jiang and Y. Tang, "An interval type-2 fuzzy model of computing with words," Information Sciences, 2014. [ Links ]
[3] J. Mendel and D. Wu, Perceptual computing: aiding people in making subjective judgments, vol. 13. John Wiley & Sons, 2010. [ Links ]
[4] G. Klir and B. Yuan, Fuzzy sets and fuzzy logic, vol. 4. Prentice Hall New Jersey, 1995. [ Links ]
[5] L. Di Lascio, A. Gisolfi, and A. Nappi, "Medical differential diagnosis through type-2 fuzzy sets,"in Fuzzy Systems, 2005. FUZZ'05. The 14th IEEE International Conference on, pp. 371-376, IEEE, 2005. [ Links ]
[6] F. Doctor, H. Hagras, D. Roberts, and V. Callaghan, "A type-2 fuzzy based system for handling the uncertainties in group decisions for ranking job applicants within human resources systems," in Fuzzy Systems, 2008. FUZZ-IEEE 2008.(IEEE World Congress on Computational Intelligence). IEEE International Conference on, pp. 481-488, IEEE, 2008. [ Links ]
[7] R. Chen, P. Liu, and S. Tang, "An evaluation method for enterprise knowledge management performance based on linguistic variable," in Business and Information Management, 2008. ISBIM'08. International Seminar on, vol. 1, pp. 510-513, IEEE, 2008. [ Links ]
[8] S.-Y. Wang, "Applying 2-tuple multigranularity linguistic variables to determine the supply performance in dynamic environment based on product-oriented strategy," Fuzzy Systems, IEEE Transactions on, vol. 16, no. 1, pp. 29-39, 2008. [ Links ]
[9] C. Li, G. Zhang, J. Yi, and M. Wang, "Uncertainty degree and modeling of interval type-2 fuzzy sets: definition, method and application," Computers & Mathematics with Applications, vol. 66, no. 10, pp. 1822-1835, 2013. [ Links ]
[10] J. Qin and X. Liu, "Interval type-2 relational analysis and its application to multiple attribute decision making," in Fuzzy Systems (FUZZ-IEEE), 2014 IEEE International Conference on, pp. 306-313, IEEE, 2014. [ Links ]
[11] D. Wu and J. M. Mendel, "A comparative study of ranking methods, similarity measures and uncertainty measures for interval type-2 fuzzy sets," Information Sciences, vol. 179, no. 8, pp. 1169-1192, 2009. [ Links ]
[12] J. M. Mendel and D.Wu, "Determining interval type-2 fuzzy set models for words using data collected from one subject: Person fous," in Fuzzy Systems (FUZZ-IEEE), 2014 IEEE International Conference on, pp. 768-775, IEEE, 2014. [ Links ]
[13] C. Desimpelaere and T. Marchant, "An empirical test of some measurement-theoretic axioms for fuzzy sets," Fuzzy sets and systems, vol. 158, no. 12, pp. 1348-1359, 2007. [ Links ]
[14] L. A. Zadeh, "Fuzzy sets," Information and control, vol. 8, no. 3, pp. 338-353, 1965. [ Links ]
[15] R. E. Bellman and L. A. Zadeh, "Decision-making in a fuzzy environment," Management science, vol. 17, no. 4, p. 141, 1970. [ Links ]
[16] J. C. Figueroa-García and G. Hernández, "A multiple means transportation model with type-2 fuzzy uncertainty," in Supply Chain Management Under Fuzziness, pp. 449-468, Springer, 2014. [ Links ]
[17] J. C. Figueroa-García, E. J. Medina-Pinzón, and J. D. Rubio-Espinosa, "Non-cooperative games involving type-2 fuzzy uncertainty: An approach," in Computer Information Systems and Industrial Management, pp. 387-396, Springer, 2014. [ Links ]
[18] D.Wu and J. M. Mendel, "Uncertainty measures for interval type-2 fuzzy sets," Information Sciences, vol. 177, no. 23, pp. 5378-5393, 2007. [ Links ]
[19] J. M. Mendel, "Uncertain rule-based fuzzy logic system: introduction and new directions," 2001. [ Links ]
[20] J. M. Mendel and F. Liu, "Super-exponential convergence of the karnik-mendel algorithms for computing the centroid of an interval type-2 fuzzy set," Fuzzy Systems, IEEE Transactions on, vol. 15, no. 2, pp. 309-320, 2007. [ Links ]
[21] J. C. Figueroa-García, Y. Chalco-Cano, and H. Román-Flores, "Distance measures for interval type-2 fuzzy numbers," Discrete Applied Mathematics, 2014. [ Links ]