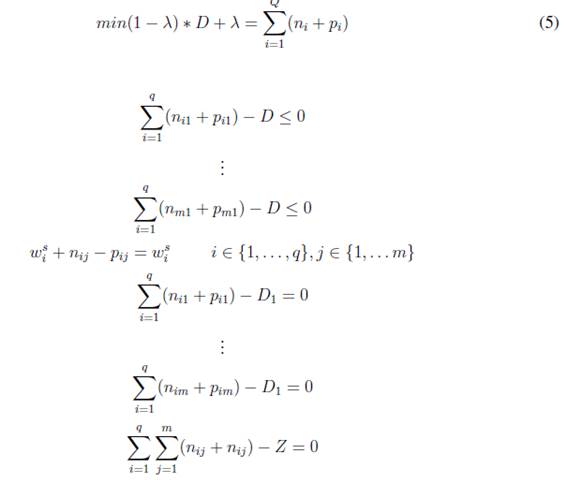1. Introducción
La demanda creciente de energía en el planeta y especialmente en Latinoamérica ofrece la probabilidad de utilizar recursos energéticos renovables; para [1], en 2012, el consumo eléctrico en esta región alcanzó los 948.000 GWh, y la energía hidroeléctrica contribuyó con el 66% de la producción total. En Centro América se elevó por arriba del 90 %, ya que es una tecnología madura y de larga duración, con algunas centrales en operación que tienen más de 100 años [2].
Por otra parte, las áreas de preocupación para los temas ambientales y sociales se relacionan por la falta de medidas de mitigación, indemnizaciones adecuadas, seguimiento y acumulación de impactos. Asimismo, en el desarrollo exitoso de un proyecto hidroeléctrico se debe reconocer la importancia en la atención de los derechos humanos [2]; en ese sentido, [3] consideran como un punto de partida para el desarrollo de la energía hidroeléctrica sustentable, la gestión integrada de recursos hidráulicos enfocados al conocimiento y racionalización del aprovechamiento de los recursos de las cuencas, además de la planeación en su desarrollo a fin de reducir su impacto. Por esta vía, la sustentabilidad hidroeléctrica está formada por tres componentes fundamentales:
La viabilidad a largo plazo del proyecto hidroeléctrico.
La contribución del proyecto al desarrollo sustentable.
La integración de las diferentes perspectivas de la sustentabilidad (ambiental, social, económica, financiera, técnica y gobernanza).
1.1. Sustentabilidad hidroeléctrica
En la década de los noventa la atención se dirigía a los aspectos de sustentabilidad relacionados con la construcción de las presas y la generación de energía hidroeléctrica. A nivel internacional, una de las primeras iniciativas para definir el problema y las medidas de mitigación para hacerle frente, fue la implementación del acuerdo sobre tecnologías hidroeléctricas emitida por la International Energy Agency (IEA, por sus siglas en inglés). En este sentido, entre 1998 y 2000, otra contribución importante la ofreció la Comisión Mundial de Presas (WCD, por sus siglas en inglés), además del seguimiento y el progreso de los proyectos del Programa de Naciones Unidas para el Medio Ambiente. En la segunda década del siglo XXI, la Asociación Internacional de Hidroelectricidad (IHA, por sus siglas en inglés) ofreció los instrumentos de mayor alcance e influencia que abordaron a la sustentabilidad en el sector de la hidroelectricidad [4].
El protocolo de evaluación de sustentabilidad hidroeléctrica [5], se benefició sustancialmente de muchas iniciativas más allá de la WCD, que acontecieron en la planificación de proyectos y el desempeño de la sustentabilidad hidroeléctrica. Dichas iniciativas incluyen los Principios de Ecuador, las normas internacionales de rendimiento de la International Finance Corporation (IFC, por sus siglas en inglés) , las políticas multinacionales de seguridad de los bancos de desarrollo (Banco Mundial y Banco Asiático para el Desarrollo), el Global Reporting Initiative (GRI, por sus siglas en inglés), las herramientas de evaluación de Inversión Sustentable (por ejemplo, Dow Jones Sustainability Index, FTSE4Good), las mejores prácticas del sector hidroeléctrico, así como las experiencias empresariales con enfoques anuales de evaluación y presentación de informes de sustentabilidad. El Protocolo también incorpora la última experiencia en los procedimientos de gobernanza a nivel nacional, sectorial, institucional y de gestión de proyectos.
El Protocolo del IHA contiene las directrices de sustentabilidad con las dimensiones económicas, sociales y ambientales para los nuevos proyectos hidroeléctricos, así como los procesos de gobernanza y cuestiones técnicas en la operación de las centrales hidroeléctricas. Las evaluaciones de sustentabilidad de proyectos hidroeléctricos se realizan mediante un riguroso análisis de las evidencias objetivas, buscando cuidadosamente deficiencias clave, es un proceso basado en un profundo diálogo con el jefe del proyecto y la consulta con las partes interesadas pertinentes. Además, en su etapa de planeación se requiere de análisis multicriterio en los temas de necesidad demostrada y ajuste estratégico; y emplazamiento y diseño para la toma de decisiones. El Protocolo de la IHA no pretende certificar empresas de energía en relación con los criterios de sustentabilidad, pero su mayor contribución es servir como guía para los gobiernos y planificadores en la toma de decisiones referente a la viabilidad de un proyecto en las dimensiones de la sustentabilidad, con una metodología para medir el riesgo e informar de los puntos fuertes, y de los impactos negativos del proyecto, lo que permite la comparación cuantitativa y cualitativa de los proyectos hidroeléctricos [4].
1.2. La hidroelectricidad en México
En México se presentan cambios en su parque de generación energía eléctrica bruta, de 2002 al 2017 pasó de 200.362.388 MWh a 257.416.682 MWh, lo que representa un 22,16% de incremento, se presentaron cambios en la participación de la capacidad efectiva por tecnología eléctrica; la tecnología de ciclo combinado incrementó su participación del 21,99% a un 49,88 %, lo que representa un 27,89 %; las otras tecnologías que también incrementaron su participación fueron carboeléctrica, eólica, combustión interna y fotovoltaica. La tecnología de vapor redujo su participación del 39,58% a un 16,14 %, lo que representa un -23,44 %; las otras tecnologías que también disminuyeron su participación fueron dual, turbogas, idroeléctrica, nucleoeléctrica y geotermoléctrica. En cuestión de la hidroelectricidad a pesar de incrementar su generación en un 9,6% en este periodo, su participación se redujo al 11,68% [6].
En México el instrumento de planeación del sector energético a largo plazo es la Estrategia Nacional de Energía (ENE) y la cual se renueva cada año a un horizonte de quince años [7]. Con la ENE y el Plan Nacional de Desarrollo [8], se construye el Programa Sectorial de Energía [9]. Con los anteriores documentos se realiza el Programa Especial para el Aprovechamiento de Energías Renovables [10]; a partir de la Ley para el Aprovechamiento de Energías Renovables y el Financiamiento de la Transición Energética (LAERFTE) [11] y la Ley General de Cambio Climático (LGCC) [12], se especifican los porcentajes de generación con fuentes fósiles del 65% para 2024, del 60% para 2035, y del 50% para 2050; a su vez, la LGCC establece un indicador del 35% de la contribución de tecnologías limpias para el año 2024.
Los desafíos que establecen estos objetivos para integrar las energías renovables en el Sistema Eléctrico Nacional (SEN) serán enormes. La Prospectiva de Energías Renovables [13] pronostica alternativas bajas y altas, con capacidades de 31.147 MW y 38.146 MW correspondientemente para 2026, por otro lado, la Prospectiva del Sector Eléctrico [7] indica alternativas de 26.742 MW y 54.892 MW en el mismo periodo. En ambas prospectivas, dominan las grandes hidroeléctricas y centrales eólicas. El incremento de la contribución de las energías renovables al SEN ocasionará cambios potenciales en la planeación energética, modificará los criterios de crecimiento del SEN, se modificarán las reglas de operación y control del SEN, y se requerirá de la creación de nuevos perfiles técnicos y de expertos [14].
Atendiendo el criterio del menor costo en el escenario de planeación, se imposibilita el crecimiento del SEN y el cumplir con el marco legal de la LAERFTE y la LCC, por lo anterior se promociona la integración de un conjunto de proyectos que agreguen los costos ambientales y de emisiones de carbono derivados de sus objetivos [7)].
Una vez dada la introducción al problema de la sustentabilidad hidroeléctrica a nivel mundial y del marco jurídico en la planeación del sector energía en México, en cuanto a las energías renovables y limpias, se presenta a la Coordinación de Proyectos Hidroeléctricos (CPH) y la problemática que presentan sus proyectos hidroeléctricos.
1.2.1. Los proyectos hidroeléctricos de la CFE
La Coordinación de Proyectos Hidroeléctricos (CPH), perteneciente a la Comisión Federal de Electricidad (CFE), es la responsable de planear, diseñar, supervisar y construir las obras civiles y montaje electromecánico de la infraestructura hidroeléctrica requerida para cubrir la solicitud de energía hidroeléctrica en México [15]. Las decisiones para integrar nuevos proyectos para crecer el SEN se hacen con muchos años de antelación, son extensos los periodos de tiempo desde que se decide su planeación hasta su entrada a generar. Se lleva alrededor de cuatro a siete años el análisis de las alternativas para tomar la decisión de construir una nueva central hidroeléctrica, hasta que inicia a generar. Así que, las disposiciones conllevan a una consecuencia económica de larga duración, ya que el tiempo de vida útil de las centrales hidroeléctricas puede ser mayor a 30 años [16].
Para [17], en los recientes años, se presentan demoras en los proyectos de generación eléctrica causado primordialmente por el incremento en los tiempos de tramitación de licencias de uso de suelo y permisos ambientales; aclaraciones con las comunidades indígenas afectadas; restricciones en autorizar inversiones; diferimientos en la ejecución de los trabajos constructivos; complicaciones de carácter social con autoridades municipales y propietarios de los terrenos. Con base en los cambios de la esperanza de crecimiento económico del país, que incurre de manera directa en la apreciación de la demanda eléctrica, como parte del proceso de planeación cada año se actualiza la cartera de los proyectos que entrarán a generar energía. Al observar los proyectos hidroeléctricos diferidos en los Programas de Requerimientos de Capacidad (PRC) del 2004 al 2013, se observa que, de los diecinueve proyectos programados en este periodo, solo se construyeron los Proyectos Hidroeléctricos El Cajón, en 2007, el de La Yesca en 2013 y, en 2015, se inició el proceso de construcción de Chicoasén II.
1.3. Pregunta de investigación
A partir de esta problemática, se propuso armonizar las funciones de planeación, sus impactos sociales y ambientales, se buscó complementar la evaluación de los proyectos hidroeléctricos, dejar de ser únicamente técnico- económica a una evaluación técnico-económica-social-ambiental y de gobernanza, que permita mejorar la toma de decisiones desde una visión de desarrollo sustentable. Desde este enfoque se generó la pregunta de investigación ¿cómo determinar las ponderaciones de los criterios de sustentabilidad hidroeléctrica al cuestionar a un grupo heterogéneo de expertos en la planeación de proyectos hidroeléctricos?
Para atender este cuestionamiento se presenta el marco teórico, fundamentado en los métodos AHP y GP extendido; posteriormente se da a conocer la aplicación de estos métodos y el instrumento de medición encaminados a la toma de decisiones en los proyectos hidroeléctricos enMéxico y, finalmente, se incluyen los resultados obtenidos, así como las conclusiones.
2. Marco teórico
La CPH cuenta con una cartera de proyectos hidroeléctricos, los cuales, por los impactos sociales y ambientales han ocasionado retrasos en su construcción o que sean diferidos. Por esto ya no se pueden tomar las decisiones sustentadas solamente en la parte técnico-económica de los proyectos, se requiere que estas sean más integrales desde una perspectiva de sustentabilidad hidroeléctrica, mediante la combinación de métodos AHP-GP que consigan la opinión de expertos heterogéneos en la planeación de proyectos hidroeléctricos.
2.1. Proceso de Análisis Jerárquico (AHP)
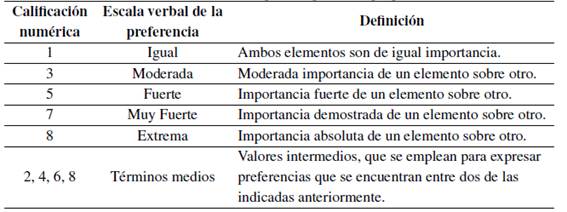
Con el propósito de afrontar problemas con múltiples criterios y una cantidad determinada de alternativas, [18] presentó el AHP, este método permite fraccionar y organizar la problemática de manera gráfica y ordenar las jerarquías. A través de comparaciones pareadas pares, establece la jerarquía e influjo de las fracciones que integran la problemática, expone reflexiones de valor que se contrastan, empleando la escala fundamental, criterios cuantitativos y cualitativos. Asimismo, accede a contrastar la consistencia de las reflexiones de valor y contribuye a mejorar la toma de la decisión [18]. Emplea escalas numéricas fundamentales para las comparaciones pareadas (Tabla I) que reflejan pensamientos, juicios e intuiciones [19[.
Para el cálculo del autovector o vector propio, se multiplica al cuadrado una matriz A de tamaño específico, a continuación, se debe normalizar las sumas de las filas para cada elemento de la matriz y de esta forma se obtiene el valor del autovector.
Para obtener el autovalor, despejar λmax de la siguiente fórmula (1 ):
Donde,
Cabe señalar, que existen por naturaleza juicios aleatorios en la toma de decisiones; los cuales en teoría se deben minimizar para que la decisión que se tome sea consistente, no obstante; es complicado pensar en alcanzar dentro de una investigación.
Resulta muy complicado alcanzar una consistencia exacta en los juicios para la toma de decisiones; sin embargo, es posible disminuir sus inconsistencias; con ese fin, se determina la inconsistencia global de los juicios a través de la proporción de consistencia, dicho porcentaje no debe superar el 10 %. Lo anterior obedece al tamaño de la matriz de comparaciones pareadas. El CI se calcula de la siguiente fórmula (2):
Donde,
La razón de consistencia CR (Consistency Ratio), se debe determinar para que los valores que superen el 10% constituyan una inconsistencia en el cálculo de los juicios y deban reevaluarse hasta conseguir coherencia y consistencia. El cálculo se efectúa con base en los valores mostrados en la Tabla II.
Con estos valores se determina la CR a través del cociente entre el CI e IA, tal como se muestra en la formula (3) [21]- [23]
Donde,
Una vez calculados los índices IC e IA, se determina la Razón de Consistencia CR, (Consistency Ratio). Los resultados pueden ser CR _ 0,10 o CR > 0,10. En el caso que el CR sea mayor al 0,10 significa que los juicios establecidos son inconsistentes, las prioridades obtenidas son inválidas en la toma de decisiones y se deberá revisar los juicios instaurados. Si el CR es igual o menor a 0,10 significa que la consistencia de las comparaciones es aceptable, las prioridades calculadas son válidas y aceptadas para la toma de decisiones.
La utilidad del AHP no se limita a ser utilizado con criterios y alternativas intangibles, por lo tanto, se utiliza para resolver problemas de toma de decisiones multicriterio, que son problemas de elección donde se evalúan las alternativas con respecto a varios criterios que pueden ser cualitativos, cuantitativos o la combinación de ambos. También, el AHP tiene el poder de tomar decisiones en grupo que permite a los tomadores de decisiones construir funciones de bienestar grupal que no violenten las condiciones de la dirección y fortalezcan las negociaciones y el aprendizaje cognoscitivo [24].
2.1.1. Etapas del AHP
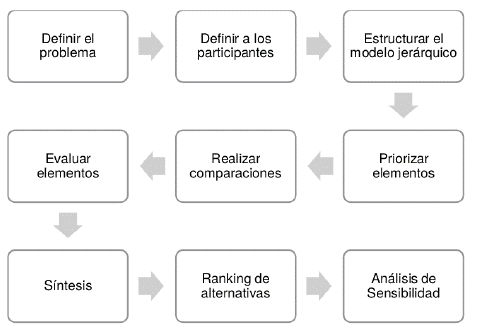
El método AHP, a través de la elaboración de un modelo de jerarquías, logra de modo eficiente y visual ordenar los elementos de un problema complejo de decidir, descomponer y analizar cada parte, representar las consecuencias de las modificaciones en las diferentes etapas y simplificar. Intenta fraccionar la problemática y después integrar todos los posibles resultados de las subproblemáticas en una sola solución. La metodología de trabajo y el procedimiento se plantea en la Figura 1.
Para [25]- [27], el AHP establece las siguientes etapas:
Definir el problema: en esta etapa se especifica el objetivo del proceso de toma de decisiones en conjunto con los participantes. Además, se debe realizar una descripción del contexto del problema.
Definición de los participantes: los participantes deben ser diligentemente escogidos, ya que de ellos depende la representatividad del modelo.
Estructurar el modelo de jerárquico: construir una estructura jerárquica que esté conformada por el objetivo, los criterios, subcriterios y alternativas. Para esto se requiere, en primer lugar, definir los criterios. Estos criterios son a nivel superior y constituyen el objetivo buscado. Una vez realizado lo anterior, se llega a un nivel o niveles específicos (subcriterios) que facilita el análisis y comprueban las alternativas.
Priorizar elementos: con la información recabada o la recopilación del conocimiento de los participantes se integran los juicios para cada comparación pareada de los criterios y subcriterios.
Realizar comparaciones: se inicia en el primer nivel donde se encuentran los criterios, se compara su importancia relativa con respecto al logro del objetivo, luego se desciende con los subcriterios, efectuando comparaciones pareadas de los criterios y subcriterios.
Evaluar elementos: las alternativas son evaluadas con base en los subcriterios, los cuales facilitan su tratamiento. A continuación, se calculan las prioridades locales y globales de cada elemento. Finalmente, se realiza una ponderación final en función del objetivo.
Síntesis: a través de las comparaciones pareadas y a la propiedad de transitividad entre los elementos, es posible establecer las prioridades para las diferentes alternativas.
Ranking de alternativas: se construye un ranking de prioridades para las diferentes alternativas, obedeciendo a la problemática presentada, seleccionando la mejor alternativa.
Análisis de sensibilidad: este análisis permite representar y comparar la sensibilidad del resultado respecto a posibles cambios en la priorización de los criterios [27]. Esta situación puede modificar el orden de las alternativas, a través de diferentes escenarios se determinan los límites para priorizar cada criterio [25]
El AHP es un instrumento metodológico que se ha aplicado en diversos países para integrar las predilecciones de los participantes incluidos en una problemática o en un procedimiento grupal de toma de decisiones.
2.2. Agregación de preferencias
El AHP puede ser aprovechado de manera particular o en grupo, con la participación de grupos de expertos, obteniendo un resultado final que será la solución que integre la opinión de aquellos. De acuerdo con [28], se puede calcular la agregación de la opinión para cada uno de los expertos de dos maneras:
Expertos homogéneos: son expertos que integran un grupo que entre ellos tienen similitudes como la formación académica, el lugar de trabajo y el objetivo de su trabajo.
Expertos heterogéneos: son expertos que integran a un grupo que posee un punto de vista distinto. Esto se debe a diferencias de su formación académica, por situaciones políticas, entre otras circunstancias.
2.2.1. Agregación de preferencias para expertos homogéneos
El método AHP, cuando persigue alcanzar una solución única la agregación se realiza de dos maneras:
Agregación de Juicios Individuales (AIJ). Desde las comparaciones pareadas individuales de cada experto, se elabora la matriz de comparaciones pareadas del grupo de expertos.
Agregación de Prioridades Individuales (AIP). Desde las matrices de comparaciones individuales de cada experto a través de la mediante la media geométrica se obtienen las prioridades del grupo.
Para [29] la Agregación de Juicios Individuales (AJI) se utiliza cuando se asume que el grupo funciona como un nuevo y único individuo. La fórmula (4) de la media geométrica es la siguiente:
Si se compara el elemento i con el elemento j, si α1 ij , α2 ij ,: : :, αN ij son los juicios individuales de los integrantes de los grupos 1, 2, : : :, N respectivamente, posteriormente, el valor combinado del juicio se ingresará en la matriz de comparación pareadas de los grupos [20].
Para este trabajo se selecciona el método AIP por su frecuencia de empleado, pues mantiene la estructura recíprocamente simétrica de las matrices de juicio [29].
2.2.2. Agregación de las preferencias para expertos heterogéneos
Cuando el método AHP se encuentra con grupos de expertos con una discrepancia entre sus ponderaciones y lo que ambicionan, encontrar una solución que no sea idónea, sino encontrar un abanico de soluciones donde se logre valorar las diferentes sensibilidades de un problema, en esta situación se empleará el método de programación por metas [29].
2.3. Programación por metas
La programación por metas fue publicada por [30], como una prolongación de la programación lineal que abarca múltiples criterios. Es empleada cuando se tiene el conflicto de lograr multiobjetivos en el mismo periodo de tiempo, para conseguirlo, el tomador de decisiones elige por proximidad metas preseleccionadas, disminuyendo su desviación. El GP pretende encontrar soluciones compromiso que, aunque no satisfagan todas las metas, sí permiten alcanzar ciertos niveles de satisfacción. La GP se ha combinado con otros métodos, como es el AHP [31].
2.3.1. GP extendido con AHP
Por otro lado, cuando existe un grupo de expertos con discrepancias importantes en sus opiniones, pero que quieren lograr una solución que no sea única, sino alcanzar un abanico de soluciones que muestre las diferentes sensibilidades de un problema planteado, en este caso se utilizará el método GP extendido.
2.3.2. GP extendido para un grupo heterogéneo de expertos
En algunas evaluaciones pueden coincidir grupos distintos de evaluadores que tienen intereses no compatibles. Por ejemplo: en la evaluación ambiental, como un espacio natural se encuentran valores distintos de acuerdo con la formación de los evaluadores sociales que participan (administradores, técnicos, empresarios, ecologistas). En estos casos fueron estudiados por [32], [33], se precisaron las matrices pareadas y los vectores propios de cada uno de los expertos que se concentran por similitud de la jerarquización y por grupo para obtener un vector agregado mediante la media geométrica. Conjuntadas las diferentes opiniones incorporadas en los vectores propios agregados, se realizó otra agregación de los grupos usando esta vez la Programación por Metas Extendida, con lo que se logró saber la solución más próxima a la opinión emitida por los diferentes expertos, así como establecer los resultados más próximos a la opinión de cada grupo de expertos. Por lo tanto:
Para agregar predilecciones de grupos homogéneos se emplea la media geométrica.
Para agregar predilecciones de grupos heterogéneos, con opiniones distintas, se emplea la Programación por Metas (GP) extendida. Las fórmulas (5) que se incluyen enseguida se emplean con ese propósito.
Sujeto a:
Donde,
D = Distancia máxima.ws
ω s i = Ponderación de cada experto por variable.
nij= Desviaciones negativas de la ponderación agregada.
pij = Desviaciones positivas de la ponderación agregada.wj
ω 𝑗 𝑖 = Ponderación agregada de cada una de las variables.
Z = Sumatoria de las desviaciones.
λ = constante (para cada valor de esta constante el modelo cambia).
Si λ = 0 emplear el GPMINMAX.
Si λ = 1 emplear el GP ponderado.
Asignando valores entre cero y uno a λ para calcular diversas soluciones.
Según [34]- [36], existen otros métodos de agregación de preferencias propuestas por otros autores, como la media aritmética o la media geométrica [28], [37], [38]. Aquí se eligió la solución propuesta mediante GP ya que, de esta manera, la solución final viene dada por la mediana, lo que permite que se vea menos afectada por datos o apreciaciones anómalas cuya existencia puede darse con relativa frecuencia en estos casos.
Para resolver problemas de GP extendido se empleó la herramienta de modelado LINGO.
2.3.3. Software LINGO
LINGO (LINear Generalize Optimizer) es un software de modelado de optimización para programación lineal, no lineal e integral. LINGO facilita un paquete integrado que incluye un potente lenguaje para expresar modelos de optimización, un ambiente con todas las funciones para construcción y edición de problemas, y un conjunto de solucionadores rápidos incorporados, capaces de resolver de manera eficiente la mayoría de las clases de los modelos de optimización [39].
2.4. Aplicación del método AHP - GP
En la literatura reciente se encontraron referencias que plantean la combinación de los métodos AHP y GP para la resolución de problemas relacionados con múltiples decisiones, por ejemplo, [38] para realizar una síntesis de decisión grupal de expertos basado en el principio de Bridgman; [40] para la selección de una casa por parte de un comprador con una serie de factores cualitativos y cuantitativos; [41] para la selección de escenarios del ciclo óptimo de combustible nuclear en Corea; [42] para ayudar a seleccionar el instrumento de control de calidad para la recopilación de información de los clientes; [43] para seleccionar la tecnología integrada en la fabricación de computadoras entre competidores; [44] para la selección de proveedores de literatura; [34] para encontrar el valor económico de un componente ambiental y sus valores parciales que lo integran; [45] para seleccionar proveedores con una variedad de factores cualitativos y cuantitativos; [46] para mejorarla evaluación de proveedores y las decisiones de asignación de pedidos de una cadena de suministro; [47] para la valorización de bienes inmuebles con información limitada en Varsovia; [48] desarrolló un modelo para diseñar y explicar la gestión de costos en la industria de electrodomésticos en Irán; [49] para seleccionar la planificación de los proyectos ferroviarios en Estambul; [50] para seleccionar la estrategia de mantenimiento en las centrales hidroeléctricas que tienen gran importancia en la combinación energética mundial y de Turquía; y [51] propone un modelo para seleccionar nuevos lugares adecuados para la eliminación de desechos infecciosos.
Como se observa, la revisión de los trabajos anteriores permitió identificar que no hay una aplicación directa del AHP-GP para la sustentabilidad hidroeléctrica, de aquí la importancia que tiene aplicarlo de manera individual o colectiva. En esta última, puede inmiscuirse un grupo de expertos heterogéneo que obtienen una solución útil, como consecuencia de la opinión de todos los expertos [31].
2.5. índice Kappa
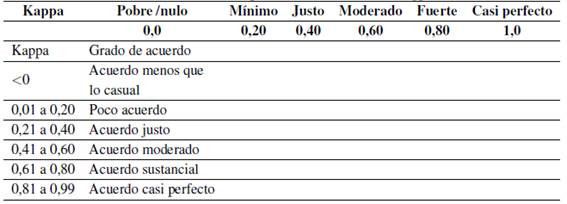
Desde su introducción en 1960, el coeficiente Kappa se convirtió en el estadístico para la evaluación de acuerdos entre jueces. [52] obtuvo la probabilidad de concordancia entre jueces; dicha probabilidad fue acreditada como el coeficiente Kappa de Cohen, es un estadístico de concordancia entre jueces que corrige el azar. Para [53], el coeficiente de Kappa es una escala de -1 a 1, donde uno indica un acuerdo perfecto, 0 es exactamente lo que se esperaría por la casualidad, y los valores negativos indican que el acuerdo obtenido será menor que el obtenido al azar, es decir, un desacuerdo sistemático potencial entre los observadores. Para facilitar su interpretación [54], propusieron la escala de valoración del coeficiente de Kappa que se indica en la Tabla III.
Al ser una probabilidad, toma su valor en el intervalo entre cero y uno. Esta se representa con la fórmula (6) siguiente:
Donde,
Po, proporción de concordancia observada
Pc, proporción esperada por el azar
K, Coeficiente de Kappa
Po se obtiene sumando los elementos de la diagonal (7):
Pc se calcula sumando el producto de las sumas marginales (8):
El grado de concordancia esperable por azar se puede calcular a partir del producto de los marginales de la matriz de confusión [55].
El coeficiente de Kappa fue empleado en el análisis de decisiones multicriterio para verificar la exactitud en los métodos en la toma de decisiones multicriterio, por ejemplo, [56] para la optimización multi-objetivo de las especificaciones técnicas y el mantenimiento utilizando algoritmos genéticos; [57] en utilizar el sistema de información geográfica en un proyecto mini-hidroeléctrico; [58] en evaluar el potencial hidroeléctrico usando GIS y la técnica de modelado hidroeléctrico; [59] para índices de consistencia para matrices de comparación pareadas; [60] ayudar a los tomadores de decisión sobre los proyectos petroleros y de gas basados en la teoría de juegos; [61] en la combinación de métodos Fuzzy y AHP para evaluar la aptitud de la tierra para el cultivo de cebada; y [62] para analizar y modelar la expansión urbana descontrolada y los cambios en el uso de la tierra en una ciudad en desarrollo.
Después de exponer la descripción del problema, así como los métodos AHP y GP, en seguida, se presenta su aplicación a grupos de expertos heterogéneos, con el objeto de obtener las ponderaciones de las perspectivas de sustentabilidad hidroeléctrica.
3. Materials and methods
3.1.1. Colectivo
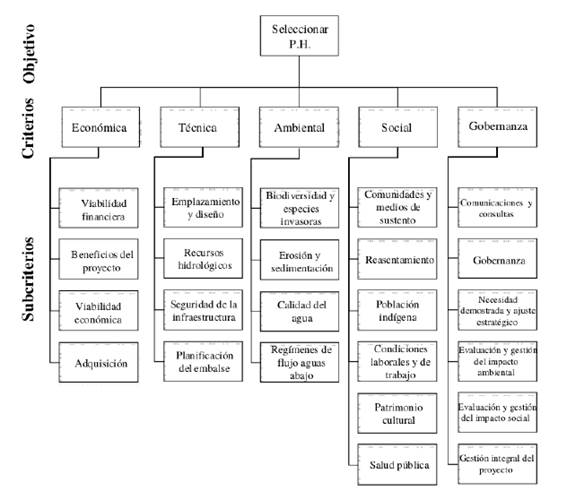
La investigación realizada se espera que ayude a los tomadores de decisión en seleccionar los proyectos hidroeléctricos, por lo que en el trabajo de campo se empleó una encuesta para determinar las ponderaciones de los cinco criterios del modelo jerárquico de sustentabilidad hidroeléctrica (Figura 2).
Con base en lo anterior, el procedimiento incluyó los criterios seleccionados para la valoración, determinados con base en las perspectivas del Protocolo del IHA [5] para la sustentabilidad hidroel éctrica como sigue:
Económica: se refiere a la viabilidad económica, incluye el análisis de costos y beneficios de los proyectos; la evaluación se hace en términos económicos o con documentos del tipo cualitativos o cuantitativos.
Técnica: se refiere a la valoración de las alternativas para satisfacer las necesidades energía y agua que toman en cuenta diferentes opciones de planeación y distintas alternativas de diseño y construcción.
Ambiental: se refiere a las cuestiones de la biodiversidad terrestre y acuática, especies en riesgo de extinción, hábitats en riesgo, integridad de los ecosistemas y aspectos de calidad del agua, conectividad, erosión y sedimentación.
Social: se refiere a aspectos de los poblados indígenas, reasentamientos humanos, comunidades impactadas, minorías étnicas, patrimonio cultural y salud pública.
Gobernanza: se refiere a la planeación, dirección y seguimiento del proyecto para la consecución de sus objetivos. También trata los aspectos de comunicación y consulta; evaluación y gestión de los impactos social y ambiental; y evaluación de los servicios energéticos e hídricos.
En este caso, se identificaron veinticuatro subcriterios (temas) en la etapa de preparación del Protocolo del IHA [5], en la perspectiva de gobernanza, el tema de evaluación y gestión del impacto social y medioambiental, se consideró necesario separar la parte social y medio ambiental (Figura 2), ya que se presentan diferencias en la gestión de estos temas en los proyectos hidroeléctricos.
Una de las etapas más importantes del método AHP, reside en estructurar la jerarquización del problema, que está integrada por el objetivo, los criterios, los subcriterios y las alternativas.
3.1. Instrumento de medición
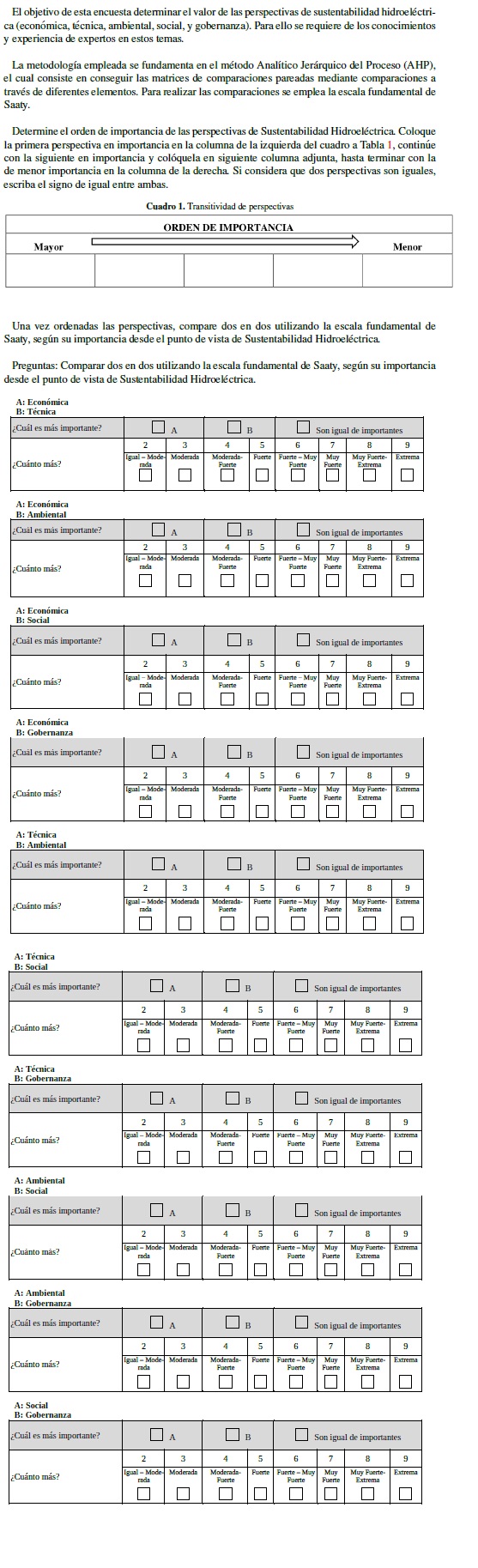
La encuesta fue el instrumento que se empleó para conseguir las matrices pareadas, requeridas en el método AHP que se describe; esto permitió determinar la importancia de cada criterio de sustentabilidad hidroeléctrica (Anexo 1). Previo a la aplicación definitiva de la encuesta se realizó una prueba piloto a un grupo de dieciocho individuos, a los que se aplicaron tres distintos diseños experimentales de la encuesta, con el objetivo de seleccionar el diseño que menor confusión presentara y arrojara la mayor consistencia.
El cuestionario fue validado por parte de seis expertos, tres expertos en hidráulica, dos en metodología y uno en métodos multicriterio. Finalmente, los expertos coincidieron en que el cuestionario era válido y aplicable; pero que necesitaba mejora. Por lo anterior, se mejoró el diseño del cuestionario, se elaboró una guía con ejemplos del llenado del cuestionario (Anexo 1) y se le adicionó una tabla de transitividad para ayudar a los participantes a respetar la jerarquía de las preferencias.
En el AHP lo primordial son los conocimientos, la experiencia y la importancia del grupo encuestado,que la cantidad de personas a entrevistar. El AHP examina a expertos referentes al objeto de estudio. Las investigaciones de tipo cuantitativo aceptan el muestro por conveniencia [63], considerando que deben buscar las unidades más representativas y convenientes para el estudio [64]. De agosto a octubre, 2017, la encuesta se aplicó de manera personalizada y por correo electrónico, con una duración media de veinte minutos por encuestado. Debido a la complejidad de los proyectos hidroeléctricos y a sus características e implicaciones políticas y sociales, se consideró oportuno realizar la encuesta a un grupo de expertos que cubriera las distintas áreas implicadas en la planeación de proyectos hidroeléctricos. Por lo que las personas encuestadas fueron 64, agrupadas de acuerdo con su especialidad.
Asimismo, la bondad de una muestra no probabilística en un estudio es que no necesita de una representatividad de los integrantes de una población, sino de una selección de elementos o personas con ciertas particularidades especificadas relacionadas al planteamiento de la problemática [65].
El grupo de expertos está integrado por diversos profesionales como: antropólogos, biólogos, sociólogos, ingenieros ambientalistas, ingenieros industriales, ingenieros civiles, ingenieros en hidráulica, ingenieros eléctricos, ingenieros electromecánicos, economistas, administradores de empresas; haciendo que se presente una diversidad de criterios y punto de vista diferentes sobre la jerarquía de cada criterio y subcriterios, inclusive dentro de cada especialidad. De los 64 expertos, 41 de ellos tienen estudios a nivel licenciatura, 21 a nivel de maestría y dos cuentan con doctorado. Su experiencia en la planeación de proyectos hidroeléctricos oscila entre los 4,59 y 26,67 años, con promedio de experiencia de 10,70 años. El 22% son mujeres y el 78% son hombres.
De este modo, se consideraron expertos del proceso de planeación responsables en la toma de decisiones y de quienes, directa e indirectamente, inciden en ella. Para esto se tienen cinco grupos de expertos:
Por último, se obtuvieron mediante la media geométrica los vectores propios. Posteriormente se planteó el modelo de GP extendido que permitió encontrar la solución útil e identificar al grupo que la propone.
4. Resultados
El análisis de los resultados aborda los siguientes aspectos:
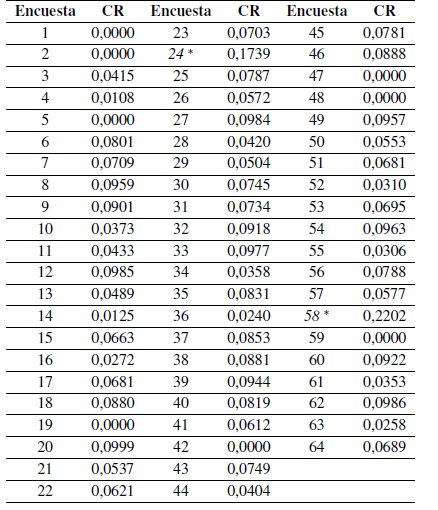
Resultados de la encuesta. Determinar la consistencia de los resultados de las comparaciones pareadas mediante la escala de Saaty (Tabla IV).
Formar grupos por especialidad y nivel jerárquico para identificar al grupo que propone la mejor solución.
Se observa en la Tabla IV que, a excepción de los encuestados 24 y 58 (en cursivas y marcadas con un _), que obtuvieron un CR superior a 10% y fueron inconsistentes, los demás alcanzaron un CR inferior o igual al 10 %. Esto dejó un total de 62 encuestas consistentes (97 %) que se agruparon según la especialidad de los encuestados en: económico, técnico, ambiental, social y gobernanza.
4.1. Resultados por grupos de expertos homogéneo por especialidad
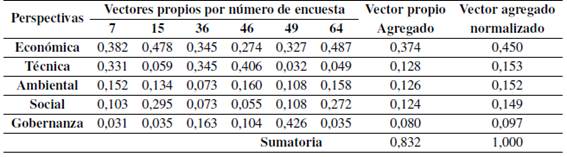
Para cada grupo de expertos se calcularon los vectores propios agregados a través de la media geométrica [18]. Se emplea la Agregación de Prioridades Individuales (AIP) para determinar el vector propio de cada matriz de los grupos de expertos, a continuación, se obtienen la media geométrica de los diferentes vectores, los resultados ya normalizados, en la Tabla V se muestra AIP para el grupo de expertos económicos.
La agregación de los expertos económicos se realizó mediante la media geométrica:
El vector propio agregado de la perspectiva económica = media geométrica (0,382; 0,478; 0,345; 0,274; 0,327; 0,487) = 0,3740
El vector propio agregado de la perspectiva técnica = media geométrica (0,331; 0,059; 0,345; 0,406; 0,032; 0,049) = 0,128
El vector propio agregado de la perspectiva ambiental = Media geométrica (0,152; 0,134; 0,073; 0,160; 0,108; 0,158) = 0,126
El vector propio agregado de la perspectiva social = media geométrica (0,103; 0,295; 0,073; 0,055; 0,108; 0,272) = 0,124
El vector propio agregado de la perspectiva de gobernanza = media geométrica (0,031; 0,035; 0,163; 0,104; 0,426; 0,035) = 0,080
El resultado no está normalizado, la sumatoria del vector propio agregado es 0,832, se necesita normalizado con la suma, como se indica en la columna del vector agregado normalizado la Tabla V.
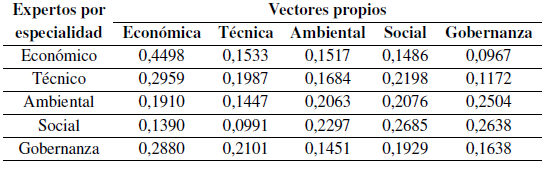
En cada grupo se calcularon los vectores propios mediante la media geométrica. Los valores normalizados de todos los grupos se presentan en la Tabla VI.
En Tabla VIse presentan los resultados por grupo de expertos: los expertos económicos y técnicos le dan mayor prioridad a la perspectiva económica y menor prioridad a la de gobernanza; los expertos ambientales le dan mayor prioridad a la perspectiva de gobernanza y menor prioridad a la técnica; los expertos sociales le dan mayor prioridad a la perspectiva social y menor prioridad a la técnica; finalmente los expertos en gobernanza le dan mayor prioridad a la perspectiva económica y menor prioridad a la ambiental.
Al comparar los resultados de los cinco grupos de expertos utilizando una matriz de concordancia (Tabla VI), se obtiene un índice Kappa de 92,82 por ciento de confiabilidad, por lo que el grado de concordancia es casi perfecto como se indica en la Tabla III.
4.1.1. Aplicación de GP extendido a grupos de expertos heterogéneo por especialidad
Se buscó la solución más próxima a la opinión emitida por los grupos de expertos por especialidad y determinar la solución más cercana a la opinión de cada grupo. Aquí también se planteó el modelo de GP extendido (5), se obtuvieron tres soluciones en función de _ (Tabla VII) mediante el software LINGO [66].
La solución fue la que presenta los valores de λ entre 0,2 a 1, en este intervalo se consiguió un valor mínimo de Z de 2,2460. Esta solución fue la más próxima a las opiniones emitidas por el grupo de expertos en gobernanza (D5). Al tomar en cuenta la mejor solución, la ponderación de las perspectivas de sustentabilidad hidroeléctrica se incluye en la Tabla VIII.
Las ponderaciones de la Tabla VIII señalan que la perspectiva mejor posicionada fue la económica, ya que obtuvo una prioridad de 29,038 %. Enseguida se ubicó la perspectiva técnica con una prioridad de 21,039 %. Finalmente, la perspectiva en el nivel más bajo fue la ambiental, con una prioridad de 14,365 %.
4.2. Análisis de las soluciones
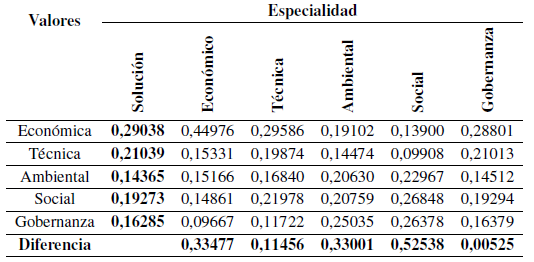
Los resultados de las 62 encuestas se organizaron en cinco grupos por especialidad. Mediante los modelos de media geométrica y GP extendido se encontró la solución útil para el grupo. En seguida, los resultados obtenidos de los grupos se comparan, enfatizando la solución que más se acerque a la opinión de cada uno de los grupos de expertos (Tabla IX).
Al comparar la solución útil con los resultados de los cinco grupos se observa que la opinión más cercana a la solución es la del grupo de expertos de gobernanza que obtuvo una diferencia de 0,00525. Por lo anterior, se afirma que la encuesta aplicada a este grupo presentó opiniones dispares. Lo anterior permitió validar el empleo de los métodos multicriterio AHP y GP extendido para determinar ponderaciones de los criterios de sustentabilidad hidroeléctrica mediante la encuesta a grupos heterogéneos de expertos.
5. Conclusiones
Los expertos en la planeación de proyectos hidroeléctricos son cada vez más conscientes sobre el desarrollo sustentable y del equilibrio que deben guardar los proyectos. La parte social de un proyecto hidroeléctrico es transcendental para poder construir las nuevas centrales hidroeléctricas. Una buena gestión e involucramiento de las partes interesadas ayudará a mejorar la toma de decisiones para seleccionar el mejor proyecto hidroeléctrico sustentable.
Los métodos AHP-GP son un enfoque que consiguen recabar la opinión de un grupo de expertos heterogéneo y así determinar las ponderaciones de los criterios de sustentabilidad hidroeléctrica mediante encuestas. El AHP permite el uso del pensamiento racional y argumentos lógicos para seleccionar criterios y determinar ponderaciones a través de comparaciones pareadas, mientras que el GP permite que obtener una solución útil de grupos heterogéneos al encuestarlos. En este contexto, se apoya del índice Kappa para evaluar los acuerdos entre jueces, y que fue empleado en otros estudios de toma de decisiones multicriterios para verificar su exactitud del método.
En relación al análisis de resultados realizado se determinó que el grupo de expertos en gobernanza es el que proponen la solución más próxima a la opinión emitida de cada grupo. De las ponderaciones obtenidas, la perspectiva mejor posicionada fue la económica con un 29,04 %, posteriormente siguió, en orden descendente, la técnica con 21,04% y finalmente la perspectiva con la menor ponderación fue la ambiental con 14,36 %.
Al pilotear la encuesta en tres ocasiones y someterla a la validez de juicios de expertos, se logró que el cuestionario fuera válido y aplicable, mejorando los diseños propuestos anteriormente [28], [31], obteniendo un 97% de cuestionarios consistentes. De acuerdo con [67], un estudio o encuesta permite obtener altos valores en validez o confiabilidad, si el diseño del estudio y el empleo de métodos estadísticos apropiados forman parte fundamental en el logro de buenos resultados.
Al cuestionar al grupo de expertos heterogéneo para determinar las ponderaciones de los criterios de sustentabilidad hidroeléctrica, se observó que se presentan acuerdos significativos entre los grupos al momento de asignar las ponderaciones, al presentar un índice Kappa = 0,9282, lo cual llama la atención por tratarse de grupos de expertos heterogéneos, ya que se esperaba un desacuerdo mayor por ser profesionales de diferentes disciplinas.
La investigación proporciona apoyo a quienes buscan evaluar la sustentabilidad de proyectos hidroel éctricos mediante el protocolo del IHA y la combinación de técnicas de toma de decisiones multicriterio empleadas para obtener las ponderaciones de los criterios de sustentabilidad hidroel éctrica. Sin embargo, en investigaciones futuras debe centrarse en comparar nuestros resultados con los resultados de otros grupos de expertos en diferentes contextos de los proyectos hidroeléctricos.
De los resultados del análisis de sensibilidad paramétrica y de cómo afecta en la toma de decisiones para seleccionar los proyectos hidroeléctricos sustentables, se deberá realizar un análisis donde se contemplen las ponderaciones de los subcriterios y alternativas (proyectos hidroeléctricos) que integran el árbol de jerarquías de sustentabilidad hidroeléctrica, así como comparar los resultados obtenidos con el método fuzzy opinion, elementos que quedan como tareas pendientes.
Teniendo en cuenta lo anterior, como posibles trabajos futuros se recomienda el uso de un método integrado por AHP-GP en el análisis de la toma de decisiones para proyectos de gran envergadura, se hace recomendable su aplicación en otros escenarios de energía, como los siguientes: comparar proyectos eléctricos de diferentes fuentes de energía y con criterios sustentabilidad energética; y definir políticas públicas para generar energías renovables y seguridad energética. Asimismo, se propone incluir para futuras investigaciones en los grupos de expertos a los responsables de establecer las políticas públicas y de la planeación en materia de energía, así como a expertos académicos en temas sociales y ambientales.