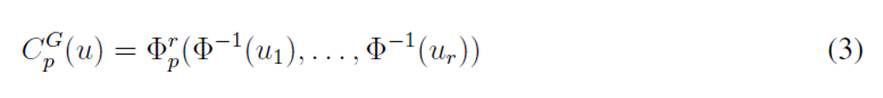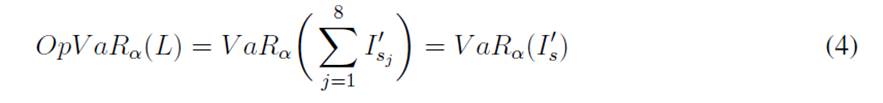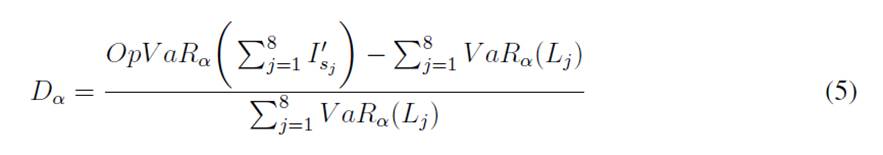Introduction
Modeling capital requirements for operational risk via the Advanced Measurement Approach (AMA) (i.e., total Operational Value at Risk, OpVaR) has been widely investigated using data from financial institutions in developed countries 1 - (3. However, the estimation of OpVaR across financial institutions in emerging markets1 has received little attention. This paper addresses this gap.
The Basel Committee on Banking Supervision (BCBS) allows banks to estimate the regulatory capital that covers their annual operational risk exposure using their own models via the AMA (Basel II/III Capital Accord 2004/2011). Among the AMA models, the Loss Distribution Approach (LDA) has been one of the most popular methods used by international banks 1, 2. Among the eligible variants of the LDA, there is a complex and reliable statistical model widely used to model dependence: copula models. The modeling of dependences between losses and the quantification of the capital to be held for covering operational risk exposure have been essential issues for both financial institutions and regulators over the past two decades 2, 4 - 7
1We follow the definition provided by Antoine van Agtmael, economist of World Bank, emerging markets are rapidly growing economies with rapid industrialization (89.
The importance of understanding, measuring, and modeling operational risk at the multivariate level is given by the high dimensions involved when constructing regulatory capital. Therefore, the main objective of this paper is to model the multivariate dependence between losses (i.e., severities) using a Gaussian copula and to calculate the capital to be held to cover operational risk exposure at financial institutions in emerging markets. The motivation for looking at these markets is because they are assuming an increasingly prominent position in global economy 8) (11. The emerging markets considered in this research are those established by the MSCI Global Investable Market Indexes’ (GIMI) Country Classification methodology (12, which are: Brazil, Chile, China, Colombia, Czech Republic, Egypt, Greece, Hungary, India , Indonesia, Malaysia, Mexico, Pakistan, Peru, the Philippines, Poland, Qatar, Russia, South Africa, South Korea, Taiwan, Thailand, Turkey, and the United Arab Emirates.
Literature review
The banking industry has had significant losses due to operational risk over the last three decades. Large-scale financial failures such as Barings, Orange County, Allied Irish Banks, Enron, and Banco Popular Español were caused for the most widely known sort of operational loss: unauthorized trading, breakdowns of internal controls, methods, and systems failures, etc. 13 - (17. Examples of financial failures caused by operational risk are also significant in emerging markets. For instance, the Inverlink financial group in Chile reported an operational loss of USD 178 million in 2003, which was caused by lost documents and privileged information (18. Brazil is the country with the highest cybernetic threats and attacks on financial institutions (17 % of total daily threats) 19. In Mexico, the number of credit card frauds was five times greater than Europe in 2018, with financial losses close to USD 250 million 20. The National Bank of Punjab in India was accused of internal fraud for USD 2.000 million 21. In Malaysia, 3.533 fraud cases in online operations were reported, causing losses amounting to USD 44 million in 2019;22.
Although financial institutions in both developed and developing countries are exposed to operational risk, only the former are obligated to comply with the guidelines of the Basel Committee on Banking Supervision (BCBS) II/ III, as those guidelines are not mandatory for financial institutions in emerging markets (23. Therefore, there is a clear gap in the adoption of regulatory guidelines by financial institutions in said markets.
BCBS II allows banks and financial institutions to estimate the capital requirements to cover operational risk exposure (OpVaR) using their own mathematical models, such as the Advanced Measurement Approach (AMA). Within the AMA approach, the Loss Distribution Approach (LDA) has become the most popular and convenient method to estimate the OpVaR [24) (26. The LDA convolutes the distribution of frequencies and distribution of severities (operational losses) into the loss aggregate distribution. There is extensive literature on this model, and some examples are published in 2, 7, 27 - (30. However, the LDA standard model suggested by BCBS II has some problems, namely (1) the model may over-estimate the OpVaR because the total potential losses are calcu lated as the sum of individual losses for every risk 24; (2) the model assumes that severities are random variables with perfect positive dependence (however, substantial literature such as 2, 6, 31, 32 has questioned such assumption); and (3) the model does not include a dependence analysis between operational losses, which produces an overestimated and conservative OpVaR calculation 33, 34.
As a result, the study of dependences between operational losses has received increased attention in the last two decades. Some studies found OpVaR reductions when using copulas for modeling dependences. 35 showed Op- VaR reductions between 20 and 29 % using t copula in three dimensions. Other authors found similar reductions using Gaussian copulas. 1 and 33 obtained OpVaR reductions between 30 and 50 %, while (36 found reductions between 7 and 11 % using Gaussian, t, and Gumbel copulas.
However, most of the research has been focused on developed countries, and, as for emerging markets, the literature is scarce. 23; studied the potential impact of implementing BCBS in emerging markets but did not include any modeling for capital estimation. 37 and 38 used copulas for estimating the value at risk in the stock market in Brazil and Mexico 37 as well as Colombia 38, but the OpVaR calculation was out of scope. Conceptual models have studied how to manage operational risk and its implications on emerging markets, and studies that have discussed the scope of the existing methods have not addressed the mathematical estimation 39, (40. Other researchers studied AMA models like LDA in emerging markets but did not include the modeling of the dependences between operational risks 26, 41, 42.
Table I shows the literature review carried out in this work. 58 bibliographic references of related topics were considered. 88 % (52 references) were based on the financial sector, and 81 % (48 references) had information on the calculation of OpVaR, that is, they focused their studies on operational risk analysis. It is clear that only 29 references (49 %) used Monte Carlo simulation in their calculations, and 25 references (42 %) applied copula models. Out of the 59 articles related to the subject, only 38 % (23 articles) focused on emerging markets.
Table I Summary of the literature review
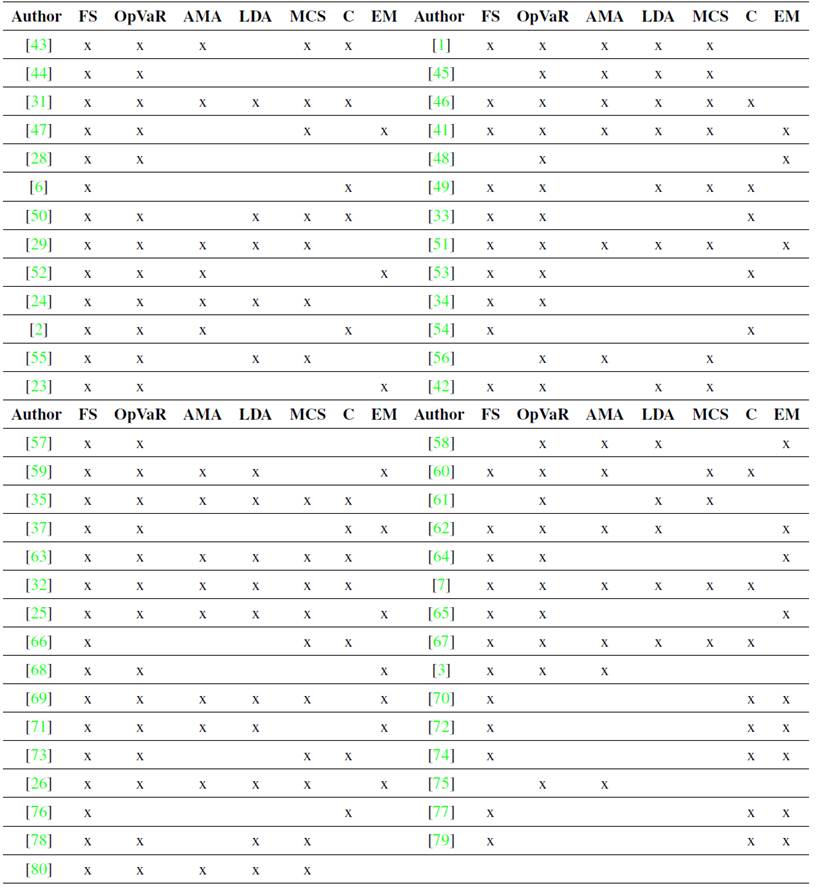
*FS: Financial Sector, OpVaR: Total Operational Value at Risk, AMA: Advanced Measurement Approach, LDA: Loss Distribution Approach, MCS: Monte Carlo simulation, C: copula, EM: emerging markets .
As a conclusion, the literature on operational risk applied to emerging markets is scarce. Moreover, we could not find literature that addresses the effect of modeling multivariate dependence between operational losses in capital risk estimation. This paper addresses this gap.
Methodology
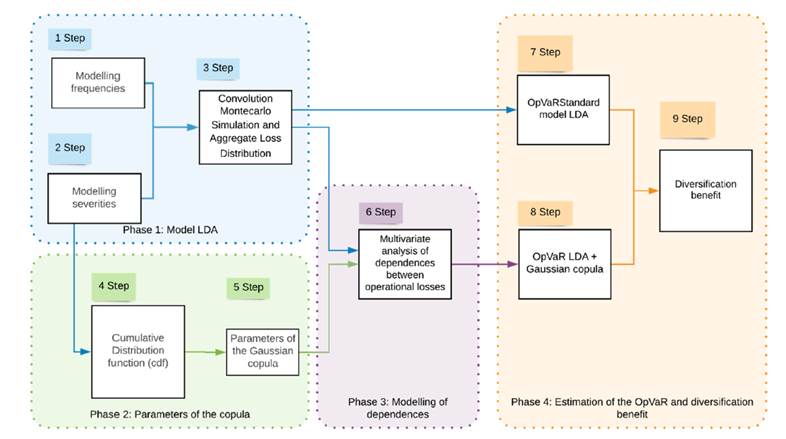
The structure of this research is outlined in Fig. 1, which facilitates the understanding of the flow throughout distinct phases and steps. In the first phase, the Standard Model of Loss Distribution Approach (LDA) (Basel II 2004) is implemented; in the second phase, the parameters of the Gaussian multivariate copula were modeled; in the third phase, the modeling of dependencies between severities was included in the LDA standard model; and finally, in the fourth phase, the capital requirement for operational risk and the diversification benefit were estimated for each model. The diversification benefit is defined as the OpVaR reduction when a copula is used 35. This paper adds value in the second and third phase, where the Gaussian copula is introduced into the standard LDA model. This model was applied to OpRisk Global Data. This database is a worldwide repository that records operational loss classification, total loss, occurrence date, country of origin, and type of industry. This paper only considered losses that occurred in emerging markets.
Phase 1: the LDA model
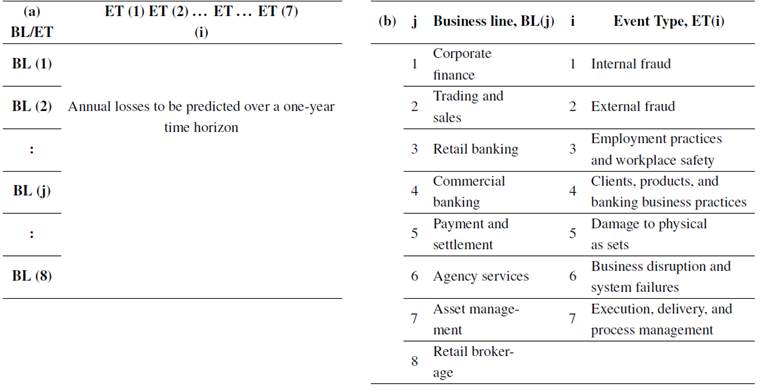
LDA is the most applied and recommended model in BCBS 4, 29, 71, 80. In the LDA model, losses are grouped into eight business lines (BL) and seven event types or risks (ET), which produces a 56-cell matrix (BL/ET). Table II shows the BL/EL matrix structure, including the detail of BL and ET.
Table II (a) Basel risk matrix of business lines (BL) and event types (ET); (b) Basel II business lines (BL) and Basel II event types (ET) - adapted from 4
The LDA model comprises three main steps 4:
Modeling frequencies: The frequency is a random variable Nj , which represents the number of loss events in a time window (frequently a year) for a BL type j. Nj is usually modeled using discrete distributions such as Poisson or negative binomial 28, 35, 50.
Modeling severities: Severity is a random variable Xkj , which represents the total amount of loss in the k loss event in the BL j. Xkj is usually modeled using continuous distributions such as exponential, gamma, inverse Gaussian, lognormal, Pareto, generalized Pareto distribution, and Weibull. LDA assumes that Xkj are independent of Nj .
Modeling the distribution of total aggregate losses: The distribution of total aggregate losses F(Lj ) is a cumulative density function (CDF) of the random loss Lj in every BL j. Lj corresponds to the following expression:
The analytical representation of F(Lj ) is difficult to determine. Therefore, it can be obtained by combining frequency and severity distributions via Monte Carlo simulation (MCS), which is widely accepted in the literature (38, 81, 82. This paper applies MCS to obtain F(Lj ). The algorithm to develop a MCS in order to obtain F(Lj ) can be found in 45.
Then, a risk measure such as value-at-risk (VaR) is calculated by taking the percentile of Lj at the desired confidence level, for example, α = 99, 9 %, for a particular business line j. Once the VaRs for each business line are estimated, the total operational risk exposure (OpVaR) is computed as
where α is the confidence level.
Model (2) is the standard approach suggested by the Basel II Accord, which works under the assumption of perfect positive dependence.
Phase 2: Gaussian copula parameters
Modeling the dependence between distribution functions using copulas allows decomposing joint probability distributions in their marginals and then joining them with a copula function 83. To obtain a copula from two or more random variables, the marginal distributions should be extracted following the procedure proposed by 84 (illustrated for a bivariate copula). Next, a brief description of this procedure is provided. Taking two probability distributions in a function of two variables F(x, y) with functions of marginal distribution u = g(x), v = h(y), g and h determine the shape of the distribution F(x, y). Isolating the copula function implies vanishing the effect of g and h over the F(x, y). To this end, the inverse functions g −1 and h −1 are first obtained from x = g −1 (u) and y = h −1 (v). u and v are the probability for each value on x and y, which means that u and v are distributed in a uniform way between (1. The next step is to obtain F(x, y) = F(g −1 (u), h−1 (v)), which means a copula C(u, v). According to 85, every function F with marginals F1, . . . , Fr could be written as F(x1, . . . , xr) = C(F1(x1), . . . , Fr(xr)). Consequently, any copula C could be used to join a set of univariate distribution functions like this: C(u) = C(u1, . . . , ur) = F(F −1 2 (u1), . . . , F −1 r (ur)).
Following (7, the r-dimensional Gaussian copula takes the form of
where Φ −1 is the inverse of a standard Gaussian univariate CDF, and Φp is the standardized multivariate Gaussian distribution function with a P correlation matrix. Thus, the parameter that needs to be estimated for the Gaussian copula is P. See 86 and 87 for more information about the properties of the Gaussian copula.
Phase 3: Modelling LDA using the Gaussian copula
This paper follows 51 to assess the OpVaR when dependence is involved using a Gaussian copula (see the aforementioned reference for details on the algorithm). The algorithm is summarized as follows:
Algorithm 1. LDA using Gaussian copulas
Generate a multivariate random uniform vector U with marginals which follows a uniform distribution between (1) for the specific copula C. C has a CDF called F C, and the severity of the BL type j has a CDF F(Xj ). Then Uj is calculated as follows: Uj = F(F(Xj )) for every j = 1, . . . , 8
Obtain a loss scenario l 0 sj for every BL. The l 0 sj is obtained from the inverse of Uj with the cumulative distribution function F(Lj ) calculated in Eq. (1). F(Lj ) −1 (Uj ) = l 0 s 0 for every j = 1, . . . , 8
Obtain a scenario for the total loss l 0 s , adding all de l 0 sj in each j, as follows: I 0 s = P8 j=1 I 0 sj
Repeat the three previous steps K times, for example K = 100,000.
OpVaR and diversification benefit calculation
The OpVaR estimation when multivariate dependence is explicitly included (in this case, by implementing a Gaussian copula in the LDA) is calculated as follows:
To quantify the diversification benefit, the measure proposed by (88 is adopted here. The diversification benefit is then calculated as the percentage of variation comparing Eqs. (2) and (4), as follows:
A diversification benefit would imply that high quantiles of the total annual loss distribution would be less than the sum of the corresponding quantiles of the annual loss distribution from each category. In other words, there is a diversification benefit if the VaR of the total loss (Gaussian copula model) is smaller than the sum of the individual VaR (LDA standard model).
Data
This paper analyzes the SAS® Operational Risk Global Data loss dataset (SAS OpRisk Global Data). The data contains over 29.000 operational losses greater than USD 100.000 over the period between 1900 and 2013 for firms located in emerging markets (Brazil, Chile, China, Colombia, Czech Republic, Egypt, Greece, Hungary, India, Indonesia, Malaysia, Mexico, Pakistan, Peru, the Philippines, Poland, Qatar, Russia, South Africa, South Korea, Taiwan, Thailand, Turkey, and the United Arab Emirates). The data was filtered by selecting the NAICS code 52 (financial sector), and the business lines-event types included in Table II. The filtered data has 1.320 registers with a total loss value of USD 85.000 million. Fig. 2a shows the total frequency and severity by region. The highest total value of losses and the highest number of losses are in Asia. A small quantity of frequencies was reported in Europe, America, and Africa. Fig. 2b illustrates the annual total losses in thousands of million USD as well as the frequency. It is clear that the total number of losses increased in 2009 and then declined. The sharp increase was due to the global financial crisis.
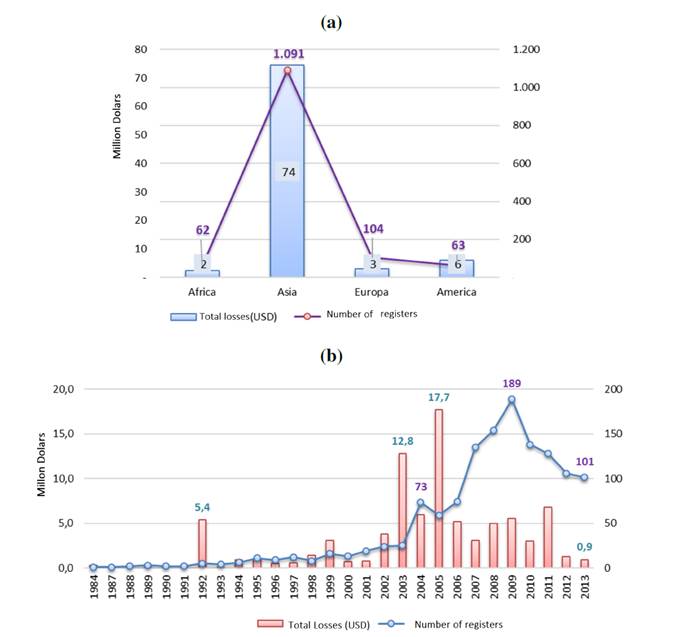
Figure 2 (a) registers by region; (b) annually aggregated number of operational risk events and total losses
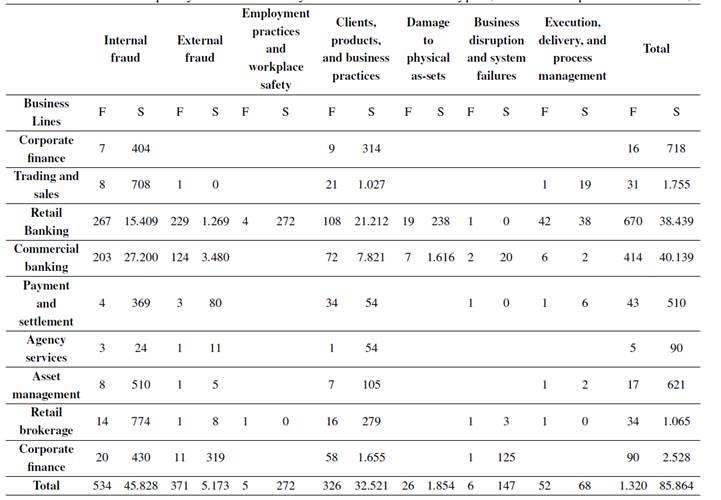
Table III shows the total frequency and total losses by business lines and event types. Table III indicates that most of the risk events come from the intersection of the business line retail banking with the internal and external fraud events (20,23 and 17,35 % of the total risk events). Such behavior indicates that fraud events are the most common operative risk events in emerging markets. It is observed that internal fraud in retail banking has the greatest impact on total losses (USD 27.200 million), followed by clients, products, and business practices in retail banking (USD 21.212 million). Such behavior indicates that the total losses produced by operational risk in emerging markets stem mainly from fraud or failures in business practices.
Gaussian copula parameters
Table IV shows the parametric distributions and the parameters that best fit the distribution of frequencies and severities, respectively.
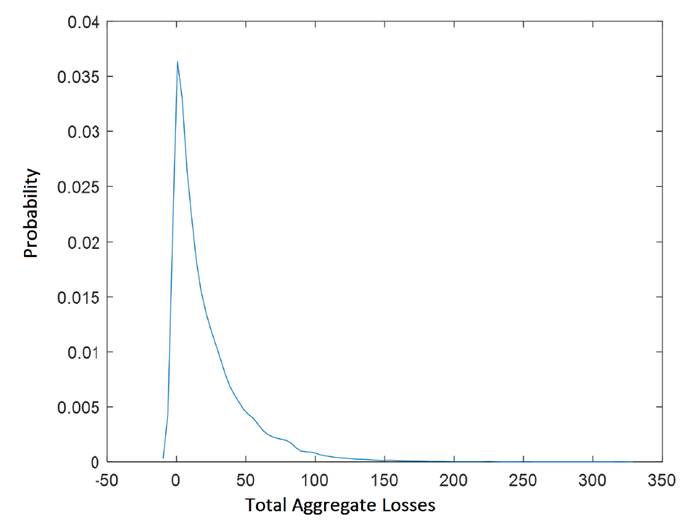
As it was explained in section 3, the total aggregated losses per business line are obtained using MCS, where the distribution of frequencies (discrete distributions) and distribution of severities (continuous distribution) are combined. Fig. 3, which shows the total aggregated losses for the business lines payment and settlement, illustrates the typical behavior of the distribution of aggregated operational losses, where high losses have a low probability of occurrence, and small losses have a high probability. The aggregated distribution in Fig. 3 was obtained after 100.000 iterations.
Table IV Results of the fitting process for event frequencies and severities (from SAS® OpRisk Global Data)
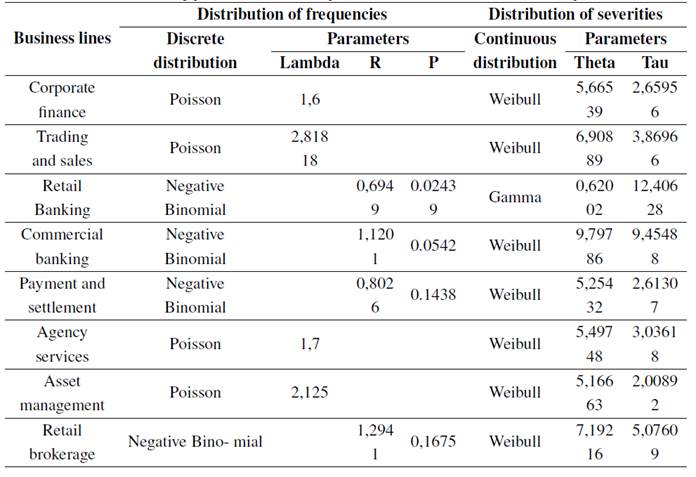
After modeling the distribution of total aggregate losses for each business line, the inputs for the standard LDA model are completed, and the parameters of the Gaussian copula are calculated.
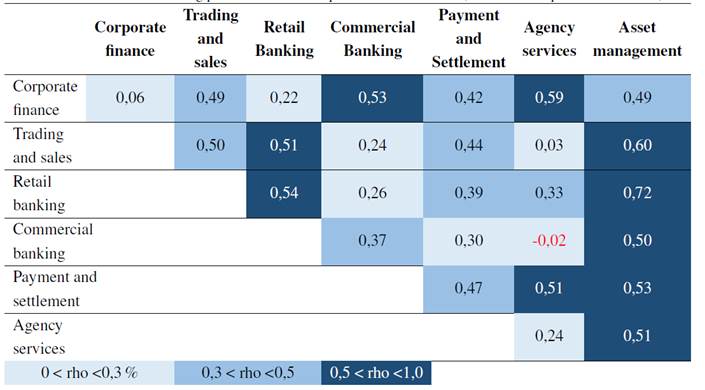
Table V shows the parameters for the Gaussian copula, the correlation matrix P. Correlation values under 0,3 indicate a low correlation, and values higher than 0,5 indicate a high correlation.
Results
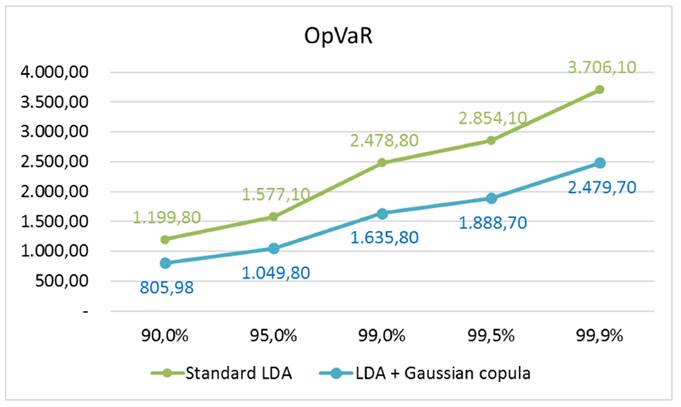
Table VI and Fig. 4 show the estimation of the OpVaR using the two discussed models: (i) estimated capital requirements for operational risk using the standard LDA model (BCBS 2004) model; (ii) the multivariate analysis of dependences between operational losses (severities) incorporated into the LDA using the multivariate Gaussian copula.
From Table VI and Fig. 4, it is clear that modeling multivariate dependence across business lines reduces the capital requirement that banks should allocate to cover operational risk exposure. Fig. 4 also shows a sharp capital increase between the 99,5 and 99,9 % percentiles for both models. Hence, the OpVaR capital difference between the Gaussian copula model and the standard LDA Basel model are more noticeable.
Table VI OpVaR - Standard LDA and Gaussian copula (from SAS® OpRisk Global Data)

*Data expressed in natural logarithm of million US dollars.
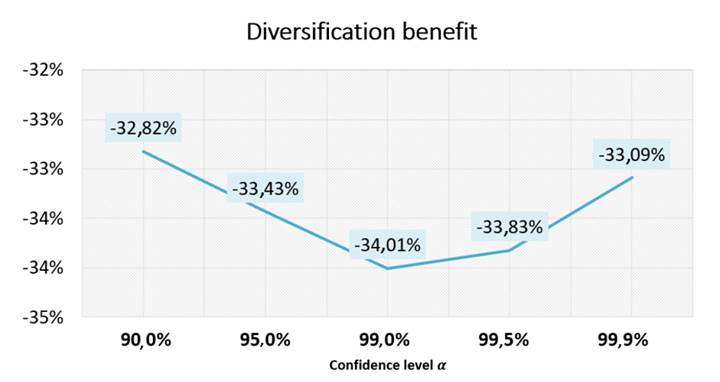
Finally, Fig. 5 shows the diversification benefit obtained from the application of the Gaussian copula model. Since the values presented in Fig. 5 are negative, the existence of the diversification benefit is corroborated. Therefore, the incorporation of dependency modeling using a Gaussian multivariate copula in the LDA standard model provides a significant reduction in capital requirement for operational risk in the financial institutions of emerging markets in comparison with the capital for operational risk estimated under the standard LDA model.
Conclusions
The main contribution of this paper is the empirical application of the modeling of multivariate dependencies between operational losses (severities) using the multivariate Gaussian copula in the estimation of operational risk capital under the Advanced Measurement Approach (AMA) in the financial institutions of emerging markets. This research presents empirical evidence in favor of a more sophisticated technique to estimate capital requirement for operational risk. Thus, tools are provided for decision-making 69 and for the management of operational risk in financial entities from emerging markets.
By incorporating the multivariate modeling of the dependency in the calculation of the OpVaR in financial entities of emerging markets, a reduction in the capital charge for operational risk was obtained (by up to 34 %) in the model that uses the Gaussian copula. Therefore, this is an important result in terms of the capital required by the financial institution that adopts this approach.
This paper makes valuable contributions to academia, since the presented results enhance the understanding of modeling operational risk in emerging markets, and researchers can use our results as a benchmark or reference framework. The results of this research are an important contribution not only for the academic community, but also for the financial entities of emerging markets, policy makers, and regulators, as it provides evidence to stride towards compliance with international standards.