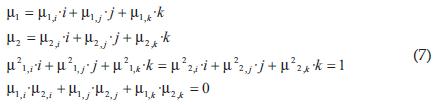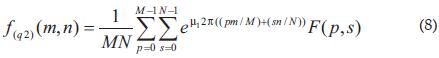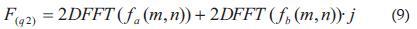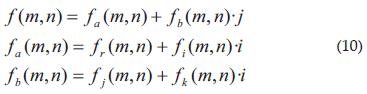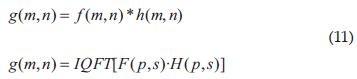Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Desarrollo
Print version ISSN 0122-3461On-line version ISSN 2145-9371
Ing. Desarro. no.23 Barranquilla June/Dec. 2008
Aplicación de los números hipercomplejos o cuaterniones en imágenes de color*
Implementation of hypercomplex or quaternion numbers in color image
Vivianne A. Mahecha1
1 Estudiante de Ingeniería Electrónica, Pontificia Universidad Javeriana, Bogotá, (Colombia). vivianne.mahecha@javeriana.edu.co
Fecha de recepción: 10 de enero de 2008
Fecha de aceptación: 25 de febrero de 2008
Resumen
Trabajar las imágenes a color en el espacio de los números hipercomplejos o cuaterniones permite que ésta sea transformada como una sola entidad sin dejar a un lado información como la tonalidad y saturación de la imagen. Por lo tanto, al implementar un sistema de detección de bordes en este espacio de cuatro dimensiones, éste resulta ser robusto a cambios de contraste y brillo en la imagen original, ya que se tiene muchas más información acerca de la imagen que la que se manejaba al detectar bordes en una imagen en escala de grises. Por otro lado, al tener el resultado final del sistema de detección de bordes con toda la información exclusiva de una imagen de color, como lo son la saturación y la tonalidad, estos bordes dan información acerca de los colores que los conforman, dando así una herramienta importante en el reconocimiento de patrones.
Palabras claves: Cuaterniones, transformada de Fourier de números hipercomplejos, operador Sobel.
Abstract
Working an image represented in the space of quaternion numbers allows it to be transform as a whole. In this case the image processing becomes more precisely as it is show in this article with an implementation of an edge detection system of a color image.
Key word: Quaternion, quaternion Fourier transform, Sobel operator.
INTRODUCCIÓN
Los números cuaterniones fueron descubiertos por William Rowarn Hamilton en 1843 [3]. Estos números representan el espacio de cuatro dimensiones y están compuestos por una parte real y tres partes imaginarias [4]:
Donde j, i, k son operadores complejos ortogonales que cumplen las siguientes condiciones
Los cuaterniones son números que permiten trabajar no sólo con tres sino también con cuatro entradas en subespacios diferentes [4], esto que en la actualidad se ha implementado en el procesamiento de imágenes a color. Una imagen a color en el plano rojo, verde y azul, más conocido como el plano RGB, por sus siglas en inglés, se representa en el espacio de los números hipercomplejos de la siguiente forma:
Por lo tanto, al implementar esta herramienta se puede trabajar la imagen como una sola entidad, convirtiéndola en un cuaternion puro, y no con sus componentes separadas o en escala de grises.
En este trabajo se emplea esta nueva herramienta para detectar bordes en imágenes de color, implementando el sistema de detección en la plataforma MATLAB. Para ello se hace una revisión de la transformada de Fourier de números cuaterniones, así como una revisión de la convolución y producto de espectros en este espacio.
Posterior a esto se presentan algunos resultados con su respectivo análisis, y se muestran ventajas y desventajas del sistema de detección.
TRANSFORMADA DE FOURIER DE NÚMEROS HIPERCOMPLEJOS, RELACIÓN ENTRE CONVOLUCIÓN Y PRODUCTO EN EL DOMINIO DE LA FRECUENCIA
A. Transformada de Fourier de números hipercomplejos
Existen tres tipos de transformada de Fourier de números hipercomplejos, ya que éstos no cumplen la propiedad de conmutación [5], [6]; por lo tanto, los tres tipos corresponden al orden en el que se lleve a cabo el producto de la señal por las exponenciales.
El primer tipo, o también llamado transformada de Fourier de dos lados, se define como:
El segundo tipo o transformada de Fourier del lado izquierdo, se define:Por último el tercer tipo o transformada de Fourier del lado derecho, se define:
Donde los números µ1 y µ2 son cuaterniones unitarios puros ortogonales entre si, es decir:
La transformada inversa de Fourier está definida para cada tipo, pero sólo se hablará de la transformada inversa correspondiente al tipo dos porque fue ésta la elegida para el desarrollo del trabajo. Y se define como:
De acuerdo con los resultados obtenidos por [1] existe una forma eficiente de calcular la trasformada de Fourier de tipo dos, la cual se ve resumida en la siguiente expresión:
Donde y corresponde a una división de la función , recordando por supuesto que ésta se define en el espacio de los números hipercomplejos:
Con lo anterior, obtener la transformada de Fourier se reduce a la suma de dos trasformadas de Fourier en dos dimensiones.
B. Relación entre convolución y producto en el dominio de la frecuencia
Una vez más, de acuerdo con el trabajo realizado por [1], la relación entre la convolución y el producto en el dominio de la frecuencia, implementando el tipo 2 de transformada, es la misma relación conocida al trabajar con números complejos, es decir:
Donde IQFT es la transformada inversa de Tipo 2 del producto de las dos funciones en el dominio de la frecuencia. Sin embargo, esta relación tiene una restricción y es que no es lineal en su totalidad como lo es la relación clásica, conocida por todos. Para que sea lineal, al multiplicar por un escalar, éste debe tener su componente j y componente k iguales a cero, de lo contrario no se cumple la propiedad de linealidad.
DESCRIPCIÓN DEL SISTEMA DE DETECCION DE BORDES
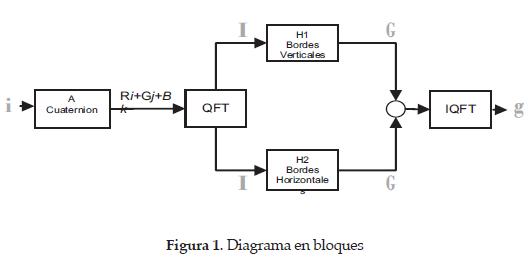
Una vez definidas las herramientas, se procede a implementar el sistema de detección en MATLAB. Este sistema ilustrado como un diagrama de bloques en la Figura 1, consiste en representar la imagen en el espacio de los números hipercomplejos.
Esto se hace extrayendo cada una de las componentes correspondientes a los colores base del plano de color en el que se esté trabajando, en este caso: rojos, azules y verdes.
De acuerdo con el trabajo realizado por [1], se halla la transformada de Fourier en números hipercomplejos de la imagen. Ya que en MATLAB aún no se han implementado los números hipercomplejos hay que tener en cuenta que el espectro obtenido después de este procedimiento debe ser dividido según lo que corresponda a cada una de las componentes en el espacio de los cuaterniones; en otras palabras, se debe especificar qué corresponde a la parte real y qué corresponde a cada una de las partes imaginarias.
Ya en el dominio de la frecuencia lo que resta es multiplicar el espectro de la imagen por el de los filtros. Estos filtros están basados en el operador "sobel", el cual calcula el gradiente de intensidad de brillo en cada píxel de la imagen. Matlab en su toolbox de procesamiento de imágenes implementa este operador aproximando dicho gradiente vertical, por lo cual resulta ser un filtro de detección de bordes horizontales.
Así, al multiplicar el espectro de la imagen por el del filtro H1, que corresponde al filtro "sobel" de MATLAB representado en el espacio de los números hipercomplejos, se tiene una detección de bordes horizontales. De igual forma, el filtro H2 corresponde al transpuesto en el dominio del tiempo del filtro h1, resultando éste un filtro para la detección de bordes verticales (Figura 2).
 (*)
(*)
Por último, se combinan estos dos resultados y se aplica la transformada inversa de Fourier (Figura 2).
ANÁLISIS DE RESULTADOS
Sistema robusto
Usualmente, cuando se trabaja una imagen a color, lo que se hace es pasarla a escala de grises y es en éste dominio en el que se caracteriza con uno u otro procesamiento. Por ser este el proceso más utilizado, se tomó como punto de referencia para compararlo con el sistema de detección de bordes desarrollado en este artículo.
El algoritmo usado por MATLAB para convertir una imagen de color a escala de grises consiste en dejar sólo la información correspondiente a la luminancia, y eliminar la información dada por la tonalidad y saturación de la imagen.
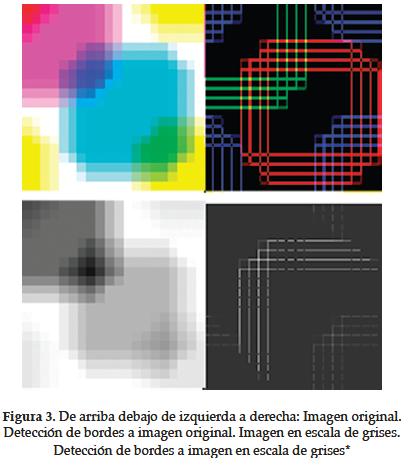
La pérdida de esta información es relevante en un sistema de detección de bordes como se ve en la Figura 3. La figura muestra cómo la imagen en escala de grises pierde claridad en los bordes por no tener información del color y la detección de bordes no es acertada.
La carencia de esta información perteneciente sólo a las imágenes de color no sólo puede llegar a ofrecer resultados erróneos si no que también puede volver a un sistema de detección de bordes sensible a cambios en la imagen original.
La Figura 4 muestra una imagen de color a la que se le alteró el brillo y el contraste y su equivalente en escala de grises. En la Figura 5 se puede ver la detección de bordes dada por los dos sistemas, la columna izquierda corresponde a la detección cuando se trabaja la imagen a color y la columna derecha corresponde al procesamiento de la imagen en escala de grises.
Como se puede ver en la Figura 5, los bordes detectados por el sistema implementado en el espacio de los números cuaterniones, independientemente del color, siempre son los mismos. Resultado que no se ve cuando se trabaja la imagen en escala de grises. Al trabajar la imagen como una sola entidad con información acerca de la luminancia, tonalidad y saturación de la misma, permite que el sistema de detección de bordes sea robusto a cambios en el brillo y contraste de la imagen.
Bordes de colores
Otro punto de comparación fue el sistema desarrollado en el libro Digital Image Processing using MATLAB [2], en el cual implementan un sistema de detección de bordes a imágenes de color, dando resultados muy parecidos al sistema realizado en este trabajo, como se muestra en la Figura 6.
El sistema desarrollado en el libro da una respuesta en escala de grises, diferente a la respuesta del sistema en el espacio de los cuaterniones; se puede observar que el color del borde da información acerca de los colores que lo conforman, por ejemplo en la Figura 6, se puede ver que si el borde está entre negro y rojo, el borde es de color rojo, si el borde está entre un negro y un rojo iluminado o naranja, el borde está en las tonalidades amarillas y si el borde está entre naranja y blanco, el borde está en las tonalidades azules.
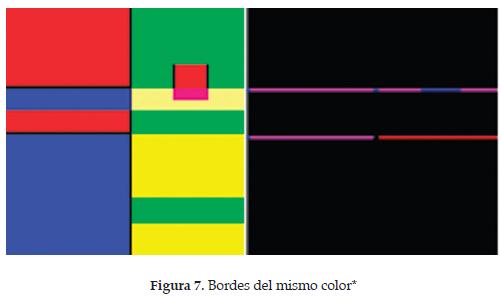
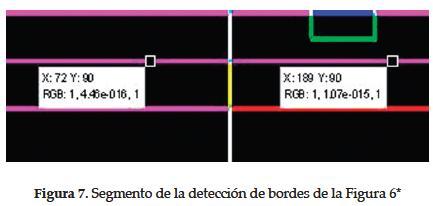
Sin embargo, este resultado no siempre es tan evidente, como se ve en la Figura 7.
Acá el borde de color fucsia describe el cambio de color azul a rojo, pero aparentemente también está describiendo el cambio de color verde a amarillo claro. No obstante, al mirar las componentes de los diferentes colores, se encontró que había una diferencia no perceptible, como se ve en la Figura 7, donde la componente correspondiente al color verde tiene una diferencia de 6.24x10-16 entre las dos imágenes. Esta diferencia se puede hacer más notoria ampliando la escala de colores.
CONCLUSIONES
Trabajar la imagen como una sola entidad, en el dominio de los números cuaterniones, independiza de cierto modo los cambios de brillo y contraste en ésta, lo cual es de suma importancia, ya que al tomar una imagen ya no va a ser objeto de preocupación el aporte de la luz, es decir, ahora se puede trabajar con la misma imagen siendo tomada en condiciones diferentes de luz.
Por otro lado, la información dada por el color del borde permite saber en dónde se encuentran los mismos colores o, más aun, si se está hablando de una aplicación específica, esta propiedad se podría usar como información acerca de patrones en la imagen.
* Nota del E.: En la versión digital de esta edición los lectores pueden ver las imágenes en color que hacen parte de este artículo. Consulte: http://uninorte/publicaciones/ingenieria-desarrollo.asp
REFERENCIAS
[1] SOO-CHANG PEI, "Efficient Implementation of Quaternion Fourier Transform", Convolution, and Correlation by 2-D Complex FFT. IEEE Transactions on Signal Processing, vol. 49, No 11, nov. 2001. [ Links ]
[2] R. GONZALES. Digital Image Processing using Matlab. New Jersey: Person Education, 2004. [ Links ]
[3] W. R. HAMILTON, Elements of Quaternions. London, U.K.: Longman, 1866. [ Links ]
[4] I. L. KANTOR and A. S. SOLODOVNIKOV, Hypercomplex Number: An Elementary Introduction to Algebras. New York: Springer-Verlag, 1989. [ Links ]
[5] S. J. SANGWINE and T. A. ELL, "The discrete fourier transform of a color image," in Image Processing II Mathematical Methods, Algorithms and Applications, J. M. Blackledge and M. J. Turner (Eds.). Chichester, U.K., 2000, pp. 430-441. [ Links ]
[6] T. A. ELL, "Quaternion-Fourier transforms for analysis of two-dimensional linear time-invariant partial differential systems," in Proc. 32nd Conf. Decision Contr., december. 1993, pp. 1830-1841. [ Links ]













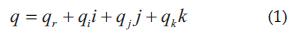 (1)
(1)
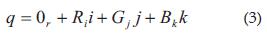
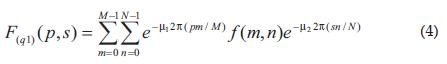
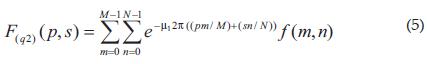
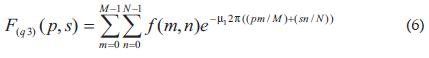 (6)
(6)