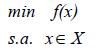Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Desarrollo
Print version ISSN 0122-3461On-line version ISSN 2145-9371
Ing. Desarro. no.24 Barranquilla July/Dec. 2008
Problema de asignación óptima de salones resuelto con Búsqueda Tabú
Course timetabling problem resolved using Tabu Search
John Fredy Franco Baquero*, Eliana Mirledy Toro Ocampo**, Ramón Alfonso Gallego Rendón***
* Estudiante de Doctorado en Ingeniería Eléctrica, Universidad Estadual Paulista (Brasil). jffranco@gmail.com
** Magister en Investigación de Operaciones y Estadística. Magister en Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Docente asistente, Facultad de Ingeniería Industrial, Universidad Tecnológica de Pereira (Colombia). elianam@utp.edu.co
*** Doctor en Ingeniería Eléctrica, Área de Automática, Universidad de Campiñas (UNICAMP). Docente titular, Facultad de Ingeniería Eléctrica, Universidad Tecnológica de Pereira (Colombia). ragr@utp.edu.co
Correspondencia: Universidad Tecnológica de Pereira, Vereda La Julia, Risaralda (Colombia).
Fecha de recepción: 30 de agosto de 2008
Fecha de aceptación: 27 de septiembre de 2008
Resumen
La asignación de salones se plantea como un problema de optimización matemática; es un problema complejo y típico de la investigación de operaciones acerda del cual muchos grupos de investigadores alrededor del mundo discuten sobre la mejor forma de resolverlo. Se presenta el modelo matemático del problema, así como una metodología basada en la Búsqueda Tabú, con el fin de encontrar soluciones factibles que minimicen la función objetivo propuesta, mediante la propuesta de constructivos, estructura de vecindad y estrategias para desenvolver el proceso de búsqueda. La calidad de las soluciones encontradas se valida y compara con casos de prueba de la literatura especializada.
Palabras claves: Búsqueda Tabú, metaheurísticas, optimización combinatorial, programación de horarios de clase.
Abstract
Classroom assignment is considered as a complex and typical mathematical optimization problem in operation research, that is tried to solve in different ways by several research groups all over the globe. A mathematical model and a methodology based on Tabú search are presented in order to find feasible solutions that minimize the objective function by using constructive algorithms, neighbor structures and other strategies that help the search process. The quality of the solutions found is validated and compared with probe cases found in the specialized literature.
Key words: Tabu Search, metaheuristics, combinatorial optimization, course timetabling,
INTRODUCCIÓN
Toda institución de educación debe poseer una suficiente cantidad de recursos en infraestructura y medios educativos que le permita impartir una educación de alta calidad. Estos recursos deberán ser lo suficientemente planificados y estudiados, a fin de que no se presente escasez o sobreoferta de ellos, pues se ocasionaría en el primer caso deterioro en la calidad de la educación y en el segundo, deterioro en sus finanzas. Las instituciones educativas en el proceso de formación proponen una serie de asignaturas o eventos que deben ser impartidos a los estudiantes adscritos a ella, porque se requiere de una infraestructura y medios educativos adecuados.
Se ha observado de tiempo atrás un crecimiento constante en la demanda de cupos estudiantiles en las instituciones de educación, que exige cuantiosas inversiones. Estas inversiones en muchos de los casos podrían diferirse en el tiempo si la institución cuenta con herramientas de trabajo que le permita planificar el uso adecuado de sus recursos, entre los que están la infraestructura física y medios educativos. Respecto a la primera, se deberá contar con una adecuada dotación de salones, laboratorios, salones multimedia y auditorios que permitan desarrollar sus labores académicas con un adecuado grado de satisfacción; su asignación deberá ser muy bien planificada a fin de establecer un uso adecuado.
Al inicio de cada período académico la administración conoce las asignaturas a las que los estudiantes desean asistir, así que debe distribuirlas dentro de su planta física en su totalidad de modo que los interesados reciban las materias que solicitaron. El modelo plantea un conjunto de restricciones denominadas duras o de obligatorio cumplimiento y un conjunto de restricciones blandas cuyo cumplimiento es optativo.
De ser satisfechas las restricciones anteriores, se dice que la propuesta planteada es factible y en estas condiciones se podrían iniciar las labores académicas. Sin embargo, usualmente se desea que los estudiantes desarrollen sus actividades de forma cómoda; para ello se plantean las restricciones denominadas blandas, que no son de obligatorio cumplimiento y, por el contrario, miden el grado de satisfacción por parte de los estudiantes. Este problema combinatorial es clasificado como del tipo no lineal entero mixto y es de difícil solución. Clasificado como NP completo, la forma de resolverlo es a través de algoritmos computacionales, es decir, los llamados algoritmos heurísticos o metaheurísticos, entre otros.
Dada la complejidad del problema, grupos de investigadores alrededor del mundo se han dado a la tarea generar metodologías capaces de resolver este problema, tratando de mejorar los resultados expuestos por otros equipos en cuanto a calidad y tiempo requerido para encontrar la respuesta. Adicional a esto, se ha creado una amplia bibliografía disponible en la página oficial de la competencia para asignación de salones (Internacional Timetabling Competition) [1], así como los casos de prueba; cabe destacar que aún no se ha encontrado una solución global para cada caso, así que el problema sigue sin resolverse por completo.
Una gran variedad de métodos se han descrito en la literatura para resolver el problema, incluso probados con casos reales. Estos métodos se dividen en cuatro tipos: métodos secuenciales [2], [3], métodos de clusterización [4], [5], métodos basados en restricciones [6], y los métodos metaheurísticos [7]. Estos últimos cuentan con un gran desarrollo en la últimas dos décadas, gracias a técnicas como recocido simulado, Búsqueda Tabú, genéticos, métodos híbridos, entre otros.
Otra característica importante encontrada en los trabajos publicados, es el enfoque del desarrollo que han alcanzado. Se pueden dividir en dos tipos: los modelos matemáticos y los heurísticos, es decir, los que tienen una base matemática o se apoyan en ella, y los que utilizan métodos algorítmicos.
En la literatura especializada ambos enfoques tienen tanto adeptos como detractores. Una de las ventajas del método matemático permite mencionarlo como el más riguroso y exacto, pero con la desventaja de su difícil formulación matemática sumada a la gran cantidad de recursos computacionales que requiere. En cambio, los heurísticos representan una facilidad para la puesta en marcha en el computador y en la confección algorítmica; sin embargo, la principal desventaja es el poco énfasis que le da al modelo matemático aún cuando este haya sido planteado desde el inicio del problema, por lo cual impide el desarrollo de una aplicación general.
Este trabajo propone una metodología para la solución del problema de asignación óptima de salones usando la técnica de optimización combinatorial Búsqueda Tabú. Se propone un modelo matemático original que muestra las restricciones de forma explícita y compacta. Además, se plantean algoritmos constructivos para generar una configuración inicial de buena calidad y se define la estructura de vecindad para la búsqueda local con Búsqueda Tabú.
Este documento se presenta de la siguiente forma: en la sección 2 se explican algunas generalidades del problema de asignación de salones; en la sección 3 se indica el modelo matemático propuesto; en la sección 4 se presentan los conceptos básicos de la Búsqueda Tabú y su adecuación al problema específico; la sección 5 se refiere a los casos de prueba y resultados obtenidos y, finalmente, en la última parte se plantean conclusiones y futuros trabajos alrededor de la temática.
2. DEFINICIÓN DEL PROBLEMA
Los problemas de asignación de salones se asocian a la labor de organizar una secuencia de eventos (generalmente asignaturas o exámenes), en un período de tiempo determinado, satisfaciendo un conjunto de restricciones. Las restricciones comprenden hechos como evitar los choques de horario, incapacidad de las salas, infra o sobrevaloración de la carga de trabajo e inadecuada disposición para estudiantes y profesores, sub o sobreasignación de recursos o equipos, entre otros [8]. Generalmente el problema considera el siguiente conjunto de restricciones: asignación de recursos, asignación de tiempo, restricciones de tiempo entre sesiones, dispersión de las sesiones, coherencia de las reuniones, capacidad de las salas, continuidad.
2.1. Tipos de problemas de asignación de salones
Un gran número de variaciones de estos problemas han sido propuestos en la literatura [9], [10], [11], los cuales difieren del tipo de eventos, institución involucrada (universidad o escuela), y de sus restricciones. De acuerdo a lo anterior se pueden identificar tres grupos:
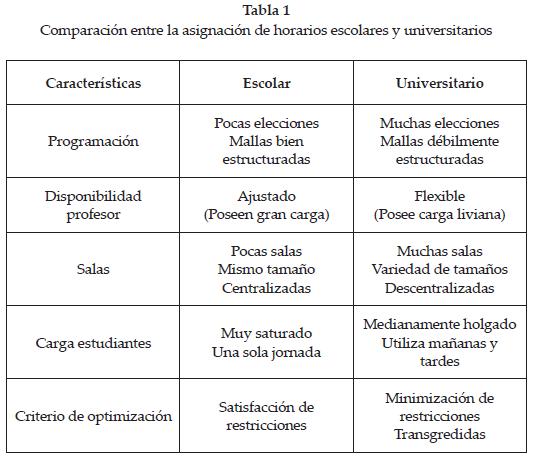
2.1.1. Asignación de horarios escolares
También conocido como Class-Teacher Problem, considera el horario semanal para las sesiones de las asignaturas de una escuela o colegio. Dada las asignaturas, profesores, bloques y una matriz de requerimientos (que establece el número de sesiones que cada profesor dicta por asignatura), el problema consiste en asignar las sesiones a los períodos de tiempo, de tal manera que ningún profesor o asignatura tenga más de una sesión en el mismo período y que todas las sesiones de la asignatura estén presentes en el horario.
2.1.2. Asignación de horarios universitarios
Este problema consiste en organizar un horario para las sesiones de un conjunto de asignaturas, considerando un número determinado de salas y bloques de tiempo. La principal diferencia entre un horario escolar y uno universitario es la forma como se considera a los estudiantes. En el ámbito escolar estos pueden considerarse una entidad, debido a que es un grupo de alumnos que toman las mismas asignaturas. En el caso universitario, generalmente con régimen semiflexible, los estudiantes toman distintas asignaturas, por lo que se generan asignaturas en común con otros estudiantes. Otra diferencia que se presenta son los profesores. En las escuelas se encargan de enseñar una asignatura y en la universidad generalmente imparten de 1 a 3 asignaturas. Además, se presenta el problema de la capacidad de las salas ya que cada asignatura tiene asociada su propio requerimiento; por el contrario, para el caso de las escuelas se pueden destinar todos los salones como aptos.
2.1.3.Asignación de horarios de exámenes
Este problema consiste en asignar el horario a los exámenes, determinando la cantidad de salas y tiempo para realizar cada examen. La cantidad de exámenes depende de los requisitos de las instituciones para evaluar los conocimientos de los alumnos que cursan una asignatura en particular con el fin de destacar las diferencias existentes entre los problemas de asignación de horarios universitarios y escolares, se describen en la tabla 1 sus principales características. Para mayor información sobre Timetabling y sus variantes, revisar el artículo realizado por Schaerf [8].
2.2. Características del problema
El modelo empleado en este trabajo se basa en el utilizado por la comunidad científica del Reino Unido que fue desarrollado para un concurso denominado International Timetabling Competition con el cual se busca resolver el problema University TT [1], planteando un conjunto de restricciones denominadas duras o de obligatorio cumplimiento y un conjunto de restricciones blandas que no son de obligatorio cumplimiento.
El conjunto de restricciones duras de estricto cumplimiento son las siguientes:
- El salón asignado debe cumplir con requisitos apropiados para desarrollar el evento tales como espacio, laboratorio, computadores, medios audiovisuales, entre otros.
- Los horarios entregados a los estudiantes no deben presentar conflictos de horarios, es decir, que un estudiante precise asistir a dos eventos diferentes a la misma hora
- Asimismo no es conveniente que en un salón se presenten dos eventos diferentes a la misma hora.
De ser satisfechas las restricciones anteriores se dice que la propuesta planteada es factible y en estas condiciones se podrían iniciar las labores académicas. Sin embargo, usualmente se desea que los estudiantes desarrollen sus actividades de forma cómoda, para ello se plantean las restricciones denominadas blandas, las cuales no son de obligatorio cumplimiento y, por el contrario, miden el grado de satisfacción por parte de los estudiantes y son las siguientes:
- La asistencia continuada a varios eventos.
- Asistir en un día a tan solo un evento.
- Asistir a un evento que se dicte en la última hora del día.
El incumplimiento de alguna de estas restricciones es penalizada por la función objetivo, incrementándola en 1, por cada restricción de este tipo que sea violada.
Según lo anterior, el caso se formula como un problema de programación de los horarios de clase, definiendo la hora y el salón para cada evento de tal forma que si se cumplen las restricciones duras, se minimizan las restricciones blandas.
3. BÚSQUEDA TABÚ
3.1. Generalidades
Búsqueda Tabú [12], [13], [14] es una técnica de optimización combinatorial que proviene de la inteligencia artificial y usa conceptos de memoria adaptativa y exploración sensible.
Un algoritmo de Búsqueda Tabú completo utiliza técnicas de exploración y de memoria avanzadas, como son: memoria de corto y largo plazo, estrategias de intensificación, diversificación, oscilación estratégica, path relinking y lista de configuraciones de élite, entre otras [12].
3.2. Función objetivo
Esta técnica resuelve problemas del tipo (1):
Donde f es una función general, lineal o no lineal, y X es un conjunto de restricciones que pueden ser lineales o no lineales también. Las variables x pueden ser de naturaleza continua, o entera o mixta. La exploración sensible de Búsqueda Tabú se basa en la idea de que una mala decisión tomada mediante una estrategia produce más información que una buena selección hecha de forma aleatoria.
3.3. Aspectos básicos de Búsqueda Tabú
3.3.1. Configuración inicial
La configuración inicial puede ser obtenida aleatoriamente, por medio de un algoritmo constructivo o alguna técnica heurística que utilice índices de sensibilidad. Una configuración aleatoria puede tener la ventaja de que evita una convergencia prematura, pero una configuración inicial de mala calidad conduce a un esfuerzo computacional mayor. Una buena configuración inicial que se encuentre con el uso de constructivo puede estar en una región promisoria y puede conducir a soluciones de alta calidad con bajos esfuerzos computacionales.
3.3.2. Generación del vecindario
Un vecino de una configuración X es una configuración X' obtenida a partir de X por medio de una transición simple. Siendo que en la mayoría de los casos el vecindario N(X) puede ser muy grande por cuanto implica un elevado esfuerzo de cómputo en el proceso de búsqueda local, se debe reducir el número de vecinos a un conjunto N*(X) más pequeño que N(X), redefiniendo el vecindario. Se tienen diferentes formas de reducir el vecindario:
- Tomar un número determinado de configuraciones seleccionadas aleatoriamente del conjunto N(X).
- Aspiración adicional. Se utiliza algún criterio como puede ser la reducción de la función objetivo hasta cierto valor. Cuando se encuentra una configuración que cumpla la condición, se evalúan otras configuraciones adicionales. Se deben fijar los números mínimo y máximo de configuraciones a ser analizadas.
- Lista de reducción de candidatos de élite. Se selecciona un conjunto de configuraciones vecinas con atributos particulares, las cuales son llamadas configuraciones de élite.
3.3.3. Selección del mejor vecino
Se evalúa cada vecino, se determina su función objetivo y se verifica si cumple las restricciones del problema a resolver para determinar la factibilidad de la configuración vecina. Los vecinos son clasificados en una lista de acuerdo con el valor de la función objetivo y el proceso selecciona el mejor candidato.
El primer candidato de la lista (de mejor función objetivo) es seleccionado siempre que el movimiento efectuado para pasar de la configuración actual a la configuración vecina no se encuentre prohibido (estado Tabú); si es factible este modo de selección, se denomina selección agresiva, que imita las características de un algoritmo goloso.
Si el mejor vecino de la lista de candidatos está clasificado como tabú por el proceso de optimización, el criterio de aspiración permite que sea seleccionado a pesar de la prohibición, si la configuración analizada mejora la configuración incumbente (es la mejor solución encontrada hasta el momento por el proceso).
Si en el vecindario generado no existe ninguna configuración que mejore la función objetivo, entonces se selecciona la mejor de las peores en tanto que no haya sido clasificada como Tabú durante el proceso de optimización. Esta estrategia evita que se quede atrapado en óptimos locales.
3.3.4. Actualización de la estructura Tabú
Búsqueda Tabú usa una estructura que tiene la misma codificación de la configuración X, para almacenar la información de los atributos que han cambiado o que han permanecido inalterables en el proceso de búsqueda. Esta información se almacena en las memorias de corto y largo plazo, las cuales pueden tener un criterio de almacenamiento fijo o variable a lo largo del proceso, dependiendo del comportamiento de la búsqueda. Esto es lo que constituye la memoria adaptativa. La memoria usada en Búsqueda Tabú puede ser explícita o por atributos [12]. La memoria explícita almacena la información completa de configuraciones élite (configuraciones de buena calidad) encontradas durante la búsqueda. La memoria basada en atributos almacena la información de los atributos que cambian al pasar de una configuración a otra, presentando como ventajas la facilidad de almacenamiento, manipulación y verificación. Con esto se evita regresar a configuraciones ya visitadas, lo cual es ventajoso; pero también se podrían dejar de conocer regiones no visitadas que tengan atributos prohibidos de aquellas ya exploradas.
4. MODELO MATEMÁTICO Y CODIFICACIÓN
La información del problema es codificada a través de matrices y vectores como se describe a continuación:
- La información de las características requeridas por los eventos se almacena en la matriz características_eventos, en la que para cada evento (filas), respecto a cada característica (columnas), aparece un '1' si el evento requiere la característica o aparece un '0' en caso contrario.
- La información de las características que tienen los salones se almacena en la matriz características_salones, en la que para cada salón (filas), respecto a cada característica (columnas), aparece un '1' si el salón tiene la característica o aparece un '0' en caso contrario.
- Se tiene un vector que indica la capacidad de los salones: capacidad_salones, en el que en la posición 'i' se almacena la capacidad del salón 'i'.
- La información de los estudiantes que están matriculados en cada evento se representa en la matriz eventos_estudiantes, en la que en la posición (i,j) tiene un '1' si el estudiante 'j' (columna) asiste al evento 'i' (fila) o tiene un '0' en caso contrario.
- A partir de las matrices características_eventos, características_salones y del vector capacidad_salones se puede crear la matriz eventos_salones que en la posición (i,j) tendrá un '1' si el evento 'i' (filas) se puede programar en el salón 'j' (columnas) o tendrá un '0' en caso contrario. Esta matriz resume las condiciones de características y capacidad de los salones frente a los eventos.
- La programación de los eventos se puede representar en una matriz (evento_hora_salón) con número de filas igual al número de eventos y con dos columnas. Para cada evento, en la primera columna se ubica la hora en la que se programa y en la segunda columna se almacena el salón donde se realiza.
- Se puede formar la matriz horario_eventos con número de filas igual al número de eventos y con 45 columnas que corresponden al total de horas. La matriz horario_eventos en la posición (i,j) tiene un '1' si el evento 'i' se programa a la hora 'j' o tiene un '0' en caso contrario.
- El horario de los estudiantes se puede generar a partir de las matrices evento_hora_salón y eventos_estudiantes, con lo que puede conocer la hora y el salón programados para cada estudiante según los eventos que tenga matriculados.
Para facilitar la comprobación de las restricciones blandas se forma la matriz horario_estudiante con número de filas igual al número de estudiantes y con 45 columnas que corresponden al total de horas. La matriz horario_estudiante en la posición (i,j) tiene un '1' si el estudiante 'i' tiene programado un evento en la hora 'j' o tiene un '0' en caso contrario. La matriz horario_estudiante se puede calcular como:
HA = EA 'ET
donde
HA : matriz horario de los estudiantes
ET : matriz horario de los eventos
EA : matriz evento estudiante
A continuación se presenta el modelo matemático para el problema de programación óptima de horarios de clase.
La restricción (1) asegura que cada evento se programa una sola vez. La restricción (2) representa la condición de que en un salón, en un bloque de tiempo, no se puede programar más de un evento. La restricción (3) permite garantizar que el salón asignado cumple con la capacidad y las características requeridas por el evento correspondiente. La restricción (4) previene que se presenten cruces de horarios para los estudiantes; esta restricción usa la matriz HA, que contiene los horarios de los estudiantes, construida según las ecuaciones (8) y (9). La ecuación (5) define la variable hf que representa el número de eventos programados al final de cada día para todos los estudiantes. La ecuación (6) define la variable hu que representa el número de eventos únicos en cada día para todos los estudiantes. La ecuación (7) define la variable hc que representa los casos en que se programan más de dos eventos consecutivos en un día para todos los estudiantes.
5. APLICACIÓN DE BÚSQUEDA TABÚ A LA PROGRAMACIÓN ÓPTIMA DE HORARIOS DE CLASE.
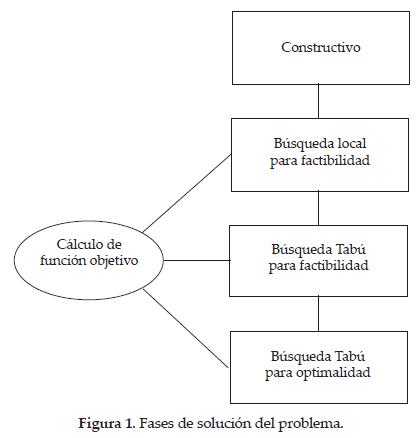
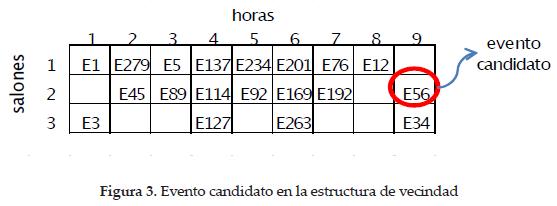
La metodología empleada para la solución del problema sigue cuatro fases. En la primera de ellas se obtiene una programación inicial de los eventos por medio de un constructivo, para que los eventos sean programados en salones habilitados, a fin de tener una configuración inicial con pocas restricciones duras violadas. En la segunda fase se emplea una búsqueda local para disminuir las restricciones duras violadas. En la tercera fase se alcanza una solución factible, en la que se cumplen todas las restricciones duras, empleando Búsqueda Tabú para minimizar restricciones duras. En la cuarta fase se usa Búsqueda Tabú para minimizar las restricciones blandas, manteniendo la factibilidad de la configuración. El desarrollo de las cuatro fases se muestra en la figura 1.
5.1. Constructivo para generar una configuración inicial
El constructivo propuesto para generar una configuración inicial sigue la idea de programar de manera prioritaria los eventos que tienen menor número de salones habilitados. Para esto se crea una lista ordenada de eventos de menor a mayor número de salones habilitados. Inicialmente se programan los eventos que solo se pueden efectuar en un determindo salón, para evitar que quede por fuera el suceso en cuestión. Una vez que se pautan los eventos que tienen un solo salón habilitado, se continúa con la programación de los siguientes acontecimientos con dos salones habilitados, luego con tres salones y así, sucesivamente, en orden creciente.
Para programar un evento primero se busca un salón habilitado usando la matriz eventos_salones y se debe encontrar un bloque de tiempo libre para asignarle, revisando que a esa misma hora no existan otros ya programados con estudiantes comunes entre ellos, usando la matriz 'estudiantes comunes'. En caso de que no se cumpla la condición anterior, el evento se deja temporalmente sin programar, para evitar generar restricciones duras de cruces de horarios de estudiantes.
Al final del proceso anterior, se buscan salones habilitados y disponibles, para ubicar los eventos aún no programados, sin importar que en el bloque de tiempo que se vaya a asignar existan actividades que ya fueron programadas y que tienen estudiantes comunes con el nuevo evento a incluirse. Debido a que es posible que no se encuentren salones habilitados que estén disponibles para algunos eventos no programados, entonces se buscan salones disponibles aunque no sean preparados para su desarrollo.
Como resultado de la programación efectuada, se tendrán algunos eventos en un salón que no está habilitado para ellos. El siguiente objetivo del constructivo consiste en asignar salones adecuados para todos los eventos. Por ello se buscan los sitios adecuados para las actividades con salones no habilitados a partir del intercambio de los lugares entre dos de esos eventos, usando la matriz eventos_salones, de tal manera que ambas actividades resulten programadas en instalaciones habilitadas. En caso de que aún se tengan problemas con los salones y no existan intercambios que solucionen estos problemas, se identifican las horas disponibles en todos los lugares, para intentar mover eventos sin problemas a otro sitio habilitado para ello. De tal forma, en el espacio dejado por estos eventos se pueden programar otros que tenían problemas locativos. Finalmente, el constructivo entrega una configuración inicial en la que todos los eventos se encuentran programados en salones habilitados, por lo que no se violan restricciones duras del segundo tipo (compatibilidad entre eventos y salones), pero pueden existir cruces de horarios para los estudiantes (violación de restricciones duras del tercer tipo).
En la figura 2 se muestra un diagrama del constructivo propuesto para generar una configuración inicial.
5.2. Evaluación de la función objetivo.
Para evaluar la función objetivo de una programación de horarios, se cuentan las restricciones duras y blandas que son violadas. Se empieza por revisar las restricciones duras de la configuración, verificando si el salón en el que se programa cada evento está habilitado, es decir, si tiene las características y la capacidad requeridas para su desarrollo; por esto se usa la matriz evento_ salón. Luego se revisa si existen cruces de horarios para los estudiantes, analizando para cada hora si los eventos programados en todos los salones en dicho lapso tienen estudiantes en común. De esta manera, se detecta un cruce de horarios para dichos estudiantes mediante la matriz estudiantes comunes. Para lograrlo se analizan todas las posibilidades de combinaciones de dos salones a la misma hora; la ventaja de revisar esta restricción de la manera mencionada reside en que no es necesario generar y analizar el horario de todos los estudiantes de forma explícita, sino más bien realizar el análisis desde el punto de vista de los eventos, dado que la cantidad de operaciones computacionales es menor y la evaluación de la configuración se hace más eficiente. Debido a la codificación usada, siempre se cumple que en un salón a una misma hora no se programa más de un evento, por lo que es innecesario verificar esta restricción.
Para la revisión de las restricciones blandas, se debe generar el horario de los estudiantes; conocida la programación de los eventos y los estudiantes que los asisten, se usa la matriz evento_estudiante_explicito, que guarda la información de la matriz eventos_estudiantes de manera eficiente, aprovechando su tendencia esparcidora, dado que no todos los estudiantes asisten a un evento en particular. De esta manera, la generación de los horarios se hace de forma eficiente: se revisa el de cada estudiante y día por día; si se presentan más de dos eventos consecutivos o eventos únicos, constituyen violaciones de restricciones blandas. Para conocer el número de estudiantes que tienen programados eventos en una hora final de un día, se revisa en cada salón, a la hora final de cada día, si existe un evento programado; en dicho caso, el número de restricciones blandas violadas corresponde al número de estudiantes que asisten al evento referido.
Índice de sensibilidad
De forma simultánea a la evaluación de la función objetivo de una configuración, se crea un índice para cada evento; mediante un contador que almacena el número de problemas asociados a este, teniendo índices diferentes para las restricciones duras y las blandas, según sea el tipo de problema. Con estos índices se orienta el proceso de búsqueda.
5.3. Estructura de vecindad
Ya que el constructivo permite encontrar una configuración inicial en la que los eventos no tienen problemas con los salones, es conveniente definir una estructura de vecindad en la cual las nuevas configuraciones sigan manteniendo la factibilidad, según los salones asignados, pero calibrando el tamaño del vecindario en cantidad y calidad.
El vecindario de una configuración consiste en configuraciones obtenidas haciendo pequeños cambios a la configuración actual. Un pequeño cambio en la configuración puede ser la modificación de hora o de salón para un evento. Con el fin de alterar la hora de un evento, sin que se afecte su factibilidad por el salón, se puede intercambiar el bloque de tiempo de dicho evento con el de otro suceso en el mismo lugar. También es posible variar el salón en el que se programa un evento, moviéndolo a un bloque de tiempo libre en otro sitio (o el mismo) siempre que el nuevo salón se encuentre habilitado para el evento. El movimiento anterior puede, además, implicar un cambio en la hora del evento.
Seleccionando un evento, se pueden generar configuraciones vecinas a partir de:
- Intercambio del bloque de tiempo del evento con otro suceso en el mismo salón.
- Movimiento del evento a un bloque de tiempo libre, en un salón habilitado para la actividad.
Para seleccionar los eventos que sirven para generar la vecindad se usa el índice de sensibilidad que se forma al calcular la función objetivo. De esta forma, haciendo una lista ordenada, los eventos que van a cambiar son aquellos que tienen un índice asociado mayor.
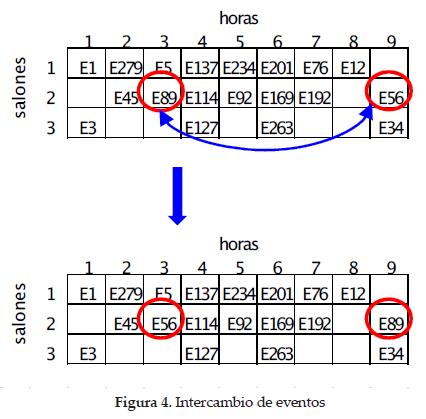
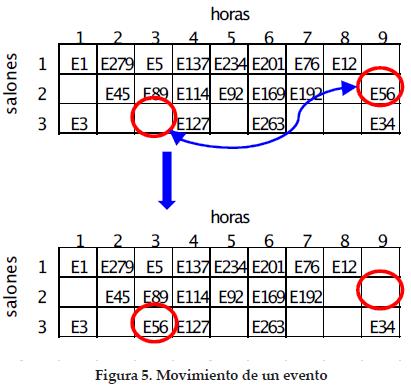
Para ilustrar la estructura de vecindad propuesta, hay que considerar la programación de los eventos mostrada en la figura 3. Suponer que el evento 56, que está programado en el salón 2 en la hora 9, es candidato para generar configuraciones vecinas. Suponer, además, que el evento 56 puede programarse en los salones 2 y 3.
Se puede generar una nueva configuración intercambiando los bloques de tiempo de los eventos 56 y 89 que están en el salón 2.
Otra configuración se obtiene al mover el evento 56 de la hora nueve al espacio disponible del salón 3, en la hora 3.
5.4. Manejo de la memoria de corto plazo
La estructura de vecindad permite generar configuraciones vecinas, tomando como base la configuración actual. El proceso de búsqueda local debe revisar estas configuraciones vecinas e identificar cuál de ellas es la mejor, en términos de factibilidad y de función objetivo, para seleccionarla como la siguiente configuración.
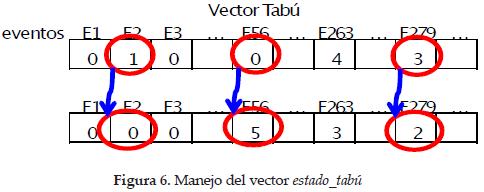
En la implementación de Búsqueda Tabú se utiliza una estructura de memoria de corto plazo que evita regresar a configuraciones ya visitadas, con lo que se puede escapar de óptimos locales en el proceso de búsqueda. La memoria de corto plazo consiste en un vector (estado _ tabú) que almacena el estado de prohibición de un evento. Cuando se ejecuta un movimiento en el que participa un evento, la posición del vector estado _ tabú asociado a ese evento cambia a un valor_tabú, el cual corresponde al número de iteraciones en que se prohíben movimientos que involucren al suceso que cambió. Siguiendo esta idea, algunas configuraciones vecinas se prohíben, en virtud de que son generadas con el movimiento de un evento que se encuentra proscrito. El valor_tabú mencionado es un parámetro de control de Búsqueda Tabú, que debe afinarse para obtener buenos resultados. Los elementos del vector estado _ tabú diferentes de cero se disminuyen en una unidad en cada iteración hasta que lleguen a cero, estado en el que se permiten movimientos que cambien la programación del evento relacionado.
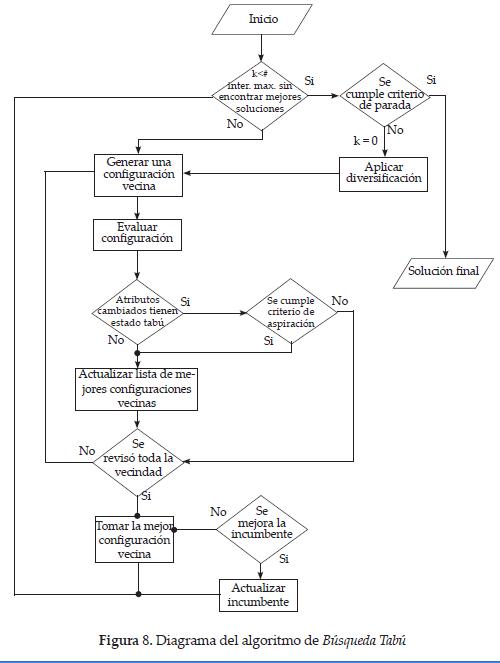
Dependiendo del tamaño de la estructura de vecindad y del valor _ tabú seleccionado, se tendrán configuraciones vecinas no prohibidas, generadas a partir de cambios en eventos no proscritos. En la figura 6 se muestra el manejo del vector estado _ tabú considerando el movimiento representado en la figura 5 (evento 56). En la figura 8 se presenta el diagrama de Búsqueda Tabú empleado, que es el mismo en las fases de búsqueda de factibilidad y luego búsqueda de optimalidad, cambiando únicamente el criterio para seleccionar la mejor configuración según la función objetivo: restricciones duras o restricciones blandas violadas.
5.5. Criterio de aspiración
Si se da el caso en que la mejor configuración vecina se encuentre prohibida, y su función objetivo mejora la mejor función objetivo encontrada hasta el momento en la búsqueda (valor de la incumbente), el criterio de aspiración permite seleccionar esta configuración a pesar de estar excluída.
5.6. Diversificación usando memoria basada en frecuencia
Cuando la función objetivo no mejora después de una cantidad determinada de iteraciones siguiendo el proceso de Búsqueda Tabú basado en memoria de corto plazo, es conveniente emplear diversificación a partir de la memoria de largo plazo basada en frecuencia.
La memoria propuesta basada en frecuencia almacena el número de veces en que la programación de un evento ha sido modificada. Esta memoria se implementa en un vector con dimensión igual al número de eventos. En la figura 7 se muestra un ejemplo de la memoria de largo plazo. De la figura 7 se puede afirmar que la programación del evento1 ha cambiado 23 veces, la del evento 56 se ha alterado 4 veces, mientras que la programación del evento 3 no ha sufrido variaciones a lo largo del proceso de búsqueda.
La estrategia de diversificación emplea la memoria de largo plazo, usando un vector ordenado de forma ascendente según el número de cambios de un evento. De ese vector ordenado se toman los primeros elementos (que corresponden a aquellos sucesos que menos han cambiado) donde el número de eventos y el número de iteraciones con los que se hace diversificación, son parámetros adicionales de Búsqueda Tabú. La programación de los eventos seleccionados es cambiada de manera forzada, para que se dirija la búsqueda a regiones no visitadas (o poco frecuentadas). En el caso asociado a la figura 6, al evento 3, que no ha cambiado, se le modificará su programación.
5. PRUEBAS Y RESULTADOS
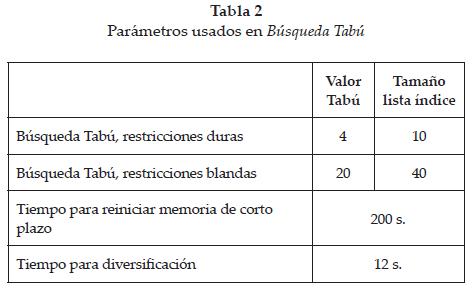
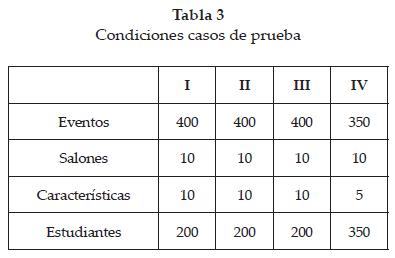
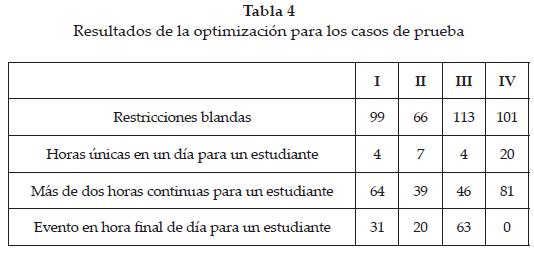
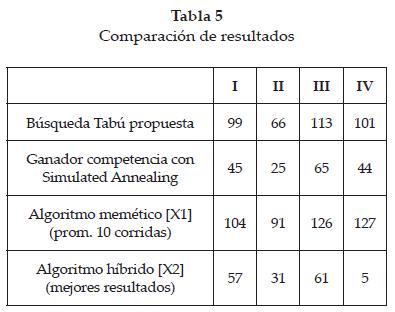
Los casos de prueba corresponden a las instancias 1, 2, 3 y 4 de la referencia [1]. Para cada uno se muestra el número de eventos, de salones, de características y de estudiantes correspondientes. Se empleó un tiempo fijo de 400 segundos para el proceso de búsqueda. En la tabla 2 se muestran los parámetros de Búsqueda Tabú empleados; la tabla 3 señala las condiciones de los casos de prueba. En la tabla 4 están los resultados obtenidos con la metodología propuesta y en la tabla 5 se presentan las comparaciones con respuestas encontradas por otras metodologías.
6. CONCLUSIONES Y RECOMENDACIONES
El problema de asignación de salones o programación de horarios de clase es de alta complejidad matemática, dadas las variables relacionadas y las condiciones involucradas. Debido a la cantidad limitada de recursos (en este caso salones), el desarrollo de metodologías que proporcionen soluciones para su adecuado aprovechamiento, satisfaciendo diferentes conjuntos de restricciones, es un área de constante investigación.
El modelo matemático planteado es una contribución al problema de programación óptima de horarios de clase, que no se encuentra en la literatura especializada. El modelo condensa las restricciones duras y blandas y muestra las relaciones entre la programación de los eventos y el horario de los estudiantes.
La estrategia para generar la configuración inicial demostró ser eficiente: realizar la programación de los eventos teniendo como prioridad evitar, en lo posible, restricciones duras y aplicar movimientos adecuados que las reduzcan, todo esto con un costo computacional ínfimo. Así, el número de iteraciones necesarias en la etapa de Búsqueda Tabú para restricciones duras es bastante pequeño comparado con estrategias que no siguen la prioridad mencionada.
El índice de sensibilidad usado para generar las configuraciones vecinas es de utilidad para guiar el proceso de búsqueda, ya que los eventos que generan más violaciones en las restricciones tienen la prioridad para generar el vecindario. Aunque las pruebas efectuadas mostraron que los mejores resultados se obtienen mediante una lista ordenada de tamaño apreciable de los eventos, que se efectúa según el índice (10%).
Los movimientos propuestos para la generación del vecindario tienen la capacidad, junto con las estrategias de Búsqueda Tabú, de escapar de óptimos locales y reducir restricciones duras y blandas, ya que permiten el cambio de salones y horas para cualquier evento. La aplicación de la estrategia de diversificación mostró ser útil cuando el proceso de búsqueda no presenta mejoras en un número determinado de iteraciones.
En trabajos futuros se pueden incluir restricciones que consideren el grado de satisfacción de los alumnos con los horarios generados, en cuanto a variables como las distancias entre salones para eventos consecutivos en los que participen. También pueden agregarse restricciones para tener bloques de eventos que conformen clases con más de una hora de duración y eventos que correspondan a clases de una misma materia, las cuales exigen su programación en bloque o en días diferentes. Debe abordarse también el problema de la programación de horarios de profesores, que es más fácil que lo tratado en este trabajo, pero que de manera conjunta con el de asignación de salones, se vuelve más complejo.
Esta nueva propuesta del modelo matemático del problema de salones es presentada con el fin de que la comunidad académica implemente nuevas técnicas de solución ya sean exactas o metaheurísticas.
REFERENCIAS
[1] Metaheuristics Network. International Timetabling Competition. Disponible en: http://www.idsia.ch/Files/ttcomp2002/ [ Links ]
[2] CARTER, M. W., LAPORTE, G., Recent developments in practical examination timetabling. In: Burke and Ross (1996) pp. 3-21. [ Links ]
[3] WERRA , An introduction to timetabling. European Journal of Operational Research 19 (1985), pp. 151-162. [ Links ]
[4] WHITE, G. M. CHAN P. W., Towards the construction of optimal examination timetables. INFOR 17 (1979), pp. 219-229. [ Links ]
[5] FISHER, J. G., SHIER, D. R., A heuristic procedure for large-scale examination scheduling problems. Technical Report 417, Department of Mathematical Sciences, Clemson University, 1983. [ Links ]
[6] WHITE, G. M., "Constrained satisfaction, not so constrained satisfaction and the timetabling problem". In: A Plenary Talk in the Proceedings of the 3rd International Conference on the Practice and Theory of Automated Timetabling, University of Applied Sciences, Konstanz, Aug., 16-18, 2000 (2000), pp. 32-47. [ Links ]
[7] BORKE, E. K., NEWALL, J. P., WEARE, R.F., 1996b. A memetic algorithm for University exam timetabling. In: Burke and Ross (1996) pp. 241-250. [ Links ]
[8] SCHAERF, Andrea, A survey of automated timetabling, Technical Report CS-R9567, CWI - Centrum voor Wiskunde en Informática, 1995. [ Links ]
[9] CARTER, M. W., LAPORTE, G., Recent developments in practical examination timetabling. In: Burke and Ross, pp. 3-21, 1996. [ Links ]
[10] CARTER, M. W., LAPORTE, G., Recent developments in practical course timetabling. In: Burke and Carter, pp. 3-19, 1996. [ Links ]
[11] WERRA, An introduction to timetabling. European Journal of Operational Research, 19, pp. 151-162, 1985. [ Links ]
[12] GLOVER, F., Tabu Search Fundamentals and Uses, University of Colorado, Boulder, Colorado, Apr. 1995. [ Links ]
[13] BAZAN, F. A. Planejamento de sistemas de distribução de energia elétrica utilizando algoritmo busca tabu, Tesis de Maestría, Universidade Estadual Paulista, 2003. [ Links ]
[14] GALLEGO, R. ESCOBAR, A. TORO, E. Técnicas metaheurísticas de optimización. Universidad Tecnológica de Pereira, 2008. [ Links ]