ARTÍCULO DE INVESTIGACIÓN / RESEARCH ARTICLE

Influencia del modelo termodinámico en la predicción de la separación
de gases de efecto invernadero por destilación

Influence of the thermodynamics model on the prediction of GHGs separation by distillation

Monica J. Valencia* Carlos A. Cardona**
Carlos A. Cardona**
Universidad Nacional de Colombia, Sede Manizales (Colombia)

* Instituto de Biotecnología y Agroindustria, Departamento de Ingeniería Química. mjvalenciab@unal.edu.co

** Instituto de Biotecnología y Agroindustria, Departamento de Ingeniería Química. ccardonaal@unal.edu.co

Correspondencia: Carlos A. Cardona. Cra. 27 No. 64-60 Manizales, Caldas (Colombia). Tel. +57 (6) 8879300 Ext. 50199.

Subvenciones y apoyos: Universidad Nacional de Colombia, Sede Manizales y Universidad de Caldas, por medio del proyecto: "Desarrollo de un proceso de obtención de alcohol carburante a partir de residuos lignocelulósicos de Caldas empleando celulasas in situ y procesos integrados, 2010-2012.

Fecha de recepción: 27 de junio de 2012
Fecha de aceptación: 24 de octubre de 2012

Resumen

La predicción de las propiedades termodinámicas de los Gases de Efecto Invernadero (GEI) es el primer paso para proponer rutas de transformación de estos compuestos en productos de valor agregado. En el presente documento se analiza la influencia del modelo termodinámico en el cálculo del equilibrio de fases sobre los resultados en la predicción de la separación de GEl's. Las ecuaciones de estado empleadas para el cálculo del equilibrio de fases de 11 mezclas (CO₂-CO-N₂O-SO₂), todas correspondientes a los gases obtenidos en procesos de combustión, fueron la ecuación de Peng-Robinson, Predictive Soave-Redlich-Kwong y Perturbed Chain - Statistical Associating Fluid Theory. Con el fin de complementar el análisis se calculó el equilibrio de fases de las mezclas binarias y ternarias que resultan de la combinación de los cuatro componentes. Posteriormente, se utiliza el diseño conceptual y las herramientas de termodinámica topológica para predecir los resultados de la separación de las mezclas, por destilación, empleando los tres modelos termodinámicos nombrados anteriormente. Los resultados indicaron que la presencia y concentración de monóxido ²²de carbono en las mezclas de GEI fueron factores determinantes a la hora de predecir el equilibrio de fases, los cuales afectaron los cálculos de la etapa de separación.

Palabras claves: Envolvente de fases, GEI, PC-SAFT, PR, PSRK, Separación por destilación.

Abstract

The prediction of thermodynamic properties can be considered as the first stage of the mitigation processes proposals. In this paper, the influence of phase equilibrium calculations over separation performance was analyzed, using Greenhouse Gases (GHG) mixtures. Eleven GHG mixtures (CO₂-CO-N₂O-SO₂) were analyzed through the Peng-Robinson, Predictive Soave-Redlich-Kwong and Perturbed Chain - Statistical Associating Fluid Theory thermodynamic models. After, topologic thermodynamics tool and conceptual design were used to predict the results of distillation separation. The thermodynamic analysis was completed with the calculations of binary and ternary phase equilibrium. The results showed the carbon monoxide concentration as issue in simulation procedure and, therefore, it affected separation calculations.

Keywords: GHG, phase envelope, PR, PC-SAFT, PSRK, Separation by distillation.

La crisis ambiental ocasionada, en parte, por la quema de combustibles de origen fósil ha generado preocupación, por la cantidad de Gases de Efecto Invernadero (GEI) descargados a la atmósfera, los cuales están relacionados con eventos extremos del clima, pérdida de productividad en cosechas, amenaza para la seguridad alimentaria, cambio en las relaciones ecosisté-micas y reincidencia de enfermedades [1], [2]. Debido a las múltiples consecuencias de las emisiones de GEI, la comunidad científica ha investigado el desarrollo de procesos alternativos, que permitan mitigar los efectos de los GEI sobre distintos sectores [3], [4].

Parte de estos esquemas de mitigación es encontrar rutas tecnológicas y económicamente viables, ya sea de origen químico, biológico o bioquímico, para disponer de los GEI o transformarlos en productos de valor agregado, reduciendo al mínimo los perjuicios ambientales. Por ejemplo, se ha considerado la captura y almacenamiento de carbón, la absorción química usando etanolaminas y el uso del dióxido de carbono como reactivo para la producción de químicos intermedios de la industria de plásticos [5], [6].

Con el fin de desarrollar rutas de mitigación y encontrar esquemas de procesos en las cuales los GEI se transformen en productos con valor agregado, es necesario disponer de toda la información preliminar requerida, es decir, predecir y validar las propiedades termodinámicas y el equilibrio de fases de los GEI [7], [8]. Ya sea la separación para la captura física del CO₂ geológica, captura química con monoetanol amina o los nuevos procesos de transformación que se están investigando, en la mayoría de estos procedimientos es necesario conocer el equilibrio de fases físico o químico de las corrientes de GEI, como primer paso en el estudio de la viabilidad tecno-económica y los beneficios ambientales de los mismos.

De lo anterior se deduce la importancia de disponer de herramientas predictivas para el cálculo del equilibrio de fases de las mezclas de GEI, como punto de partida para la consideración de esquemas de mitigación al cambio climático. Las ecuaciones de estado (EOS) son las herramientas utilizadas en el cálculo predictivo de las propiedades termodinámicas y el equilibrio de fases. Los resultados de los equilibrios de fases son requeridos para cualquier tipo de procedimiento de separación, que involucre cambio de fase.

En el presente documento se analiza el desempeño de tres Ecuaciones de Estado (EOS), Peng-Robinson (PR), Predictive Soave-Redlick-Kwong (PSRK) y Perturbed Chain - Statistical Associated Fluid Theory (PC-SAFT) para calcular el equilibrio de fases de mezclas de GEI (CO₂-CO-N₂O-SO₂) de corrientes de combustión.

Se analiza el efecto de cada uno de los modelos sobre los resultados en la predicción de la separación, por destilación. El objetivo de este trabajo fue la comparación de los resultados de los modelos termodinámicos citados (PR, PSRK y PC-SAFT) y su efecto sobre la operación unitaria (separación), con el fin de determinar aquel que mejor se ajuste para este tipo de mezcla particular y, así, disponer de un punto de partida para investigaciones sobre la transformación de GEI en productos de valor agregado.

EOS

En este trabajo se emplearon las ecuaciones PR, PSRK y PC-SAFT para calcular el equilibrio de fases de las mezclas de GEI. La naturaleza físico-química y las aplicaciones de las ecuaciones se encuentran reportadas en la literatura por diversos autores [9], [10]. En la tabla 1 se resumen todas las variables presentes en las tres ecuaciones.

Ver Tabla 1

La ecuación PR, ecuaciones (l)-(5), es una ecuación cúbica semi-empírica perteneciente a la generación de modificaciones a la ecuación de Van Der Waals, cuyas aplicaciones incluyen sustancias no polares, sustancias poco polares y las mezclas entre este tipo de componentes. Se requiere el valor de las propiedades críticas de las sustancias (Tc, Pc), el factor acéntrico (w) y dos propiedades para conocer la otra (pares T, P; v, T y P, v).

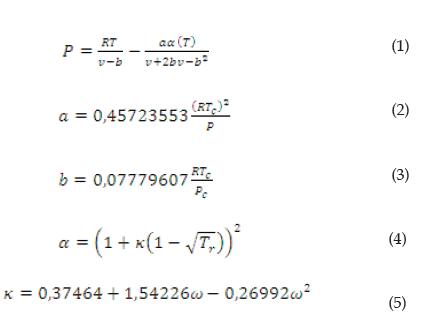
La ecuación PSRK, ecuaciones (6)-(9b), es una ecuación cúbica semi-empírica de la generación de la ecuación de Van Der Waals. Se considera una mejora a sus antecesoras debido a que incorpora métodos de contribución de grupos a su estructura, mejorando su exactitud en diversas zonas de predicción. A diferencia de la ecuación PR, esta consta de mayor cantidad de parámetros. Ya que el parámetro de interacción de las moléculas depende de la temperatura reducida (T_r) esto mejora su capacidad de predecir propiedades y puede aplicarse a sustancias polares.

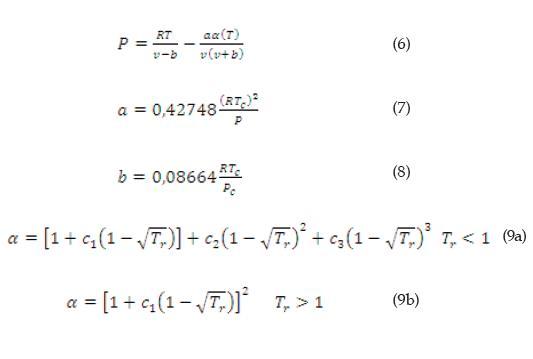
La ecuación PC-SAFT, ecuaciones (10)-(32), permite calcular propiedades termodinámicas tomando en cuenta las distintas fuerzas intramoleculares e intermoleculares de las sustancias puras y de las mezclas. El factor de compresibilidad (Z) es la suma de cuatro contribuciones: la contribución por el gas ideal (Z^id), la contribución por la formación de la cadena rígida (Z^hc), la contribución por las fuerzas de dispersión (Z^disp) y la contribución por la asociación (Z^asso). A partir de éste se calcula la propiedad deseada. Esta ecuación corresponde a una nueva generación de ecuaciones, basadas en teorías moleculares y no en ajustes exhaustivos de datos (ecuaciones semiempíricas).

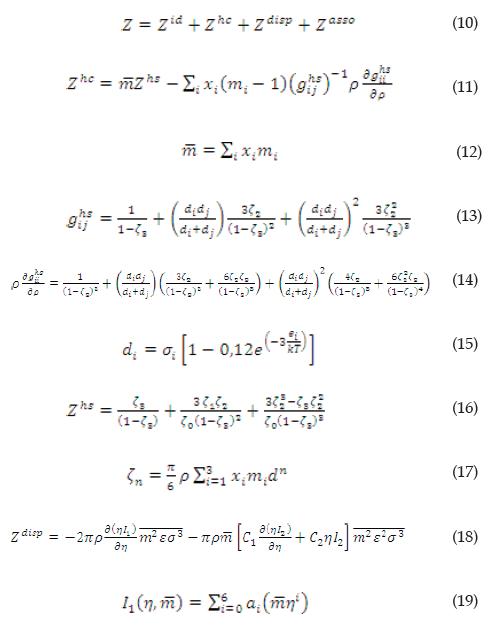
Equilibrio de fases

El cálculo del equilibrio de fases implica encontrar las condiciones de temperatura y presión para una sustancia pura o una mezcla, tal que se cumpla la condición de equilibrio, es decir, la igualdad de las fugacidades en las dos fases. El cálculo de la fugacidad depende del tipo de equilibrio que se quiera calcular (liquido-vapor, liquido-líquido u otros), del enfoque (formulación φ-φ, formulación γ-φ o formulación γ-γ) y de la ecuación de estado.

Al conjunto de estados termodinámicos de presión y temperatura de equilibrio se le conoce como envolvente de fases y permite determinar el estado termodinámico y la fase de una sustancia o mezcla en cualquier combinación de presión y temperatura

Análisis por termodinámica topológica y separación por destilación

El equilibrio de fases en diagramas termodinámicos puede ser analizado a través de unos cuantos principios topológicos, con el fin de determinar la viabilidad de la separación por destilación. A este análisis se le conoce como análisis por termodinámica topológica. Por medio del mismo, se construyen las curvas de residuo de las mezclas y la dirección de estas curvas indica la composición de las corrientes de productos en la cima y en los fondos de la columna de destilación. Las curvas de residuo se construyen a partir del equilibrio de fases con las ecuaciones presentadas en [11].

Análisis termodinámico

La elección de las ecuaciones presentadas en la sección 2 se debe a la naturaleza de cada ecuación: una ecuación empírica (PR), una ecuación empírica con base molecular (PSRK) y una ecuación molecular (PC-SAFT).

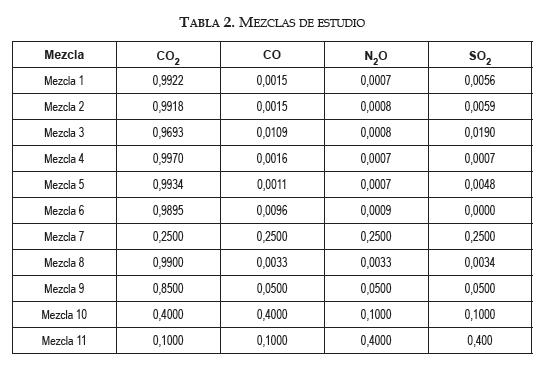
Las envolventes de fases de las mezclas cuaternarias de dióxido de carbono (CO₂) - monóxido de carbono (CO) - óxido nitroso (N₂O) - dióxido de azufre (SO₂) fueron calculadas utilizando los modelos dados por las ecuaciones (1)-(32). Las mezclas escogidas fueron 11: siete de ellas están reportadas en la literatura como gases productos de combustión [12], [13], incluyendo resultados de los esquemas tecnológicos empleados en Colombia para cogeneración con bagazo de caña. Las mezclas restantes (7-11) fueron escogidas para estudiar el comportamiento a variaciones de distintos componentes, como puede ser observado en la tabla 2. Adicionalmente, se determinó el comportamiento de las envolventes de fases ternarias y binarias para complementar los resultados de las mezclas escogidas.

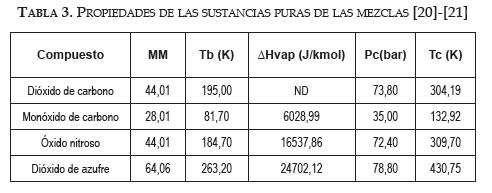
El cálculo de las envolventes fue llevado a cabo utilizando la formulación 9-9, de acuerdo a las expresiones para el coeficiente de fugacidad (9) dadas en la literatura: ecuación PR [14]; ecuación PSRK [15]; ecuación PC-SAFT [16]. Las propiedades de las sustancias puras se presentan en la tabla 3.

Para la ecuación PC-SAFT el diámetro, energía y número de segmento son parámetros requeridos que se tomaron de la literatura [17], [18]. Todas las composiciones del documento se refieren a composiciones másicas. Se determinó con cada uno de los modelos la existencia de azeótropos y se probó la consistencia de los mismos con la Ley de Vrevsky [19].

Separación

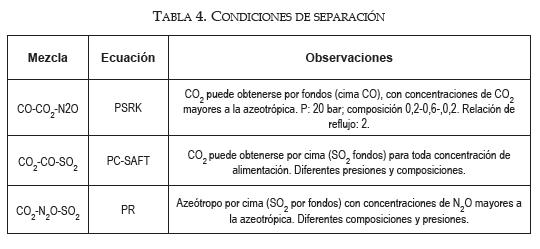
Las curvas de residuo para las cuatro combinaciones posibles de mezclas ternarias fueron generadas a dos presiones para cada uno de los modelos termodinámicos trabajados: PR, 34,7 y 70 bar; PSRK, 10 y 50 bar; PC-SAFT, 52 y 59 bar. La elección de las presiones se debe a aquellas más representativas donde se presentaban los azeótropos, que son fundamentales a la hora de la separación. Las regiones obtenidas con los análisis de los diagramas ternarios permitieron determinar las mezclas y las regiones a las cuales se llevarían a cabo el cálculo de las columnas; esta información se resume en la tabla 4. Tanto las curvas de residuo como la separación se simularon utilizando el software Aspen Plus.

Envolventes

La composición de las mezclas 1 a 5 es similar, por lo que sus envolventes se sobreponen, como puede observarse en las figuras 1, 2 y 3. La figura 1 fue obtenida calculando la envolvente con la ecuación PR, la figura 2 con la ecuación PSRK y la Figura 3 con la ecuación PC-SAFT. La presencia de N₂O y SO₂ es relativamente baja en las mezclas reportadas en la literatura; sin embargo, una pequeña variación en la composición de N₂O, SO₂ y CO cambia completamente el comportamiento termodinámico de la mezcla cuaternaria. Cuando las concentraciones de los componentes diferentes del CO₂ llegan a ser apreciables, las condiciones que predicen los modelos para la existencia del equilibrio, supera los puntos críticos de todos los componentes puros.

Ecuación PR

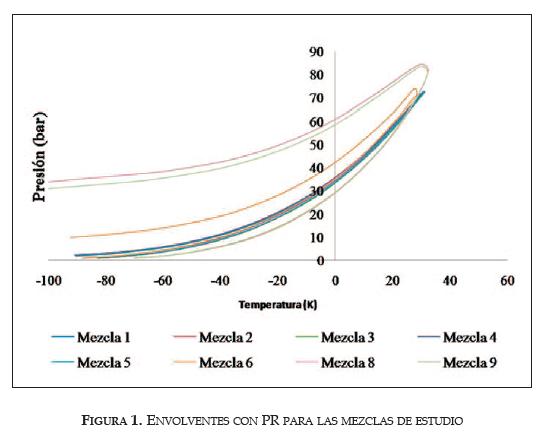
Los resultados obtenidos con la ecuación PR (ver figura 1) indicaron que cambios, tanto pequeños como grandes, en la concentración de CO, N₂O y SO₂ conlleva a predicciones cuestionables del modelo: el análisis de las mezclas de estudio y adicionales (por ejemplo 0,4-0,4-0,1-0,1 de CO₂-CO-N₂O-SO₂) mostró que, a concentraciones de CO₂ por debajo de 0,85, la ecuación PR predijo condiciones hasta 8 veces por encima del punto crítico de los componentes, invalidando con esto cualquier tipo de resultado. El análisis del comportamiento de las mezclas ternarias CO₂-CO-N₂O y CO₂-CO-SO₂, reveló que concentraciones elevadas de CO y SO₂ hicieron que el modelo no converja. En el caso de las mezclas binarias el comportamiento de la envolvente de fases depende de los componentes implicados: para la mezcla CO₂-CO el modelo es consistente a composiciones de CO₂ mayores a 0,5; las envolventes CO₂-SO₂ y N₂O-SO₂ pueden ser predichas con el modelo; las envolventes CO-SO₂ y CO-N₂O no pueden ser obtenidas por la ecuación PR y la mezcla CO₂-N₂O se comporta como un componente puro a distintas composiciones.

Los resultados obtenidos del análisis termodinámico de las mezclas cuaternarias, ternarias y binarias utilizando la ecuación PR revelaron que la concentración CO es crítica a la hora de utilizar este modelo y que el mismo no parece ser adecuado para predecir las propiedades termodinámicas de GEI con concentraciones no elevadas de CO₂.

Ecuación PRSK

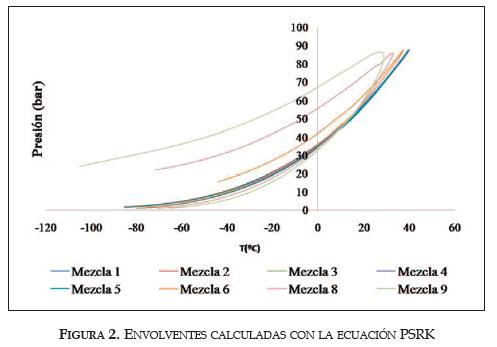
El análisis de los resultados de la ecuación PSRK (ver figura 2) mostró que, a medida que aumenta la concentración de CO, el modelo comienza a presentar fallas, tanto de consistencia termodinámica, como de convergencia del modelo. En el estudio de las envolventes binarias se obtuvieron los siguientes resultados: las envolventes CO₂-SO₂ y N₂O-SO₂ pueden ser calculadas en todo el rango; la envolvente de la mezcla CO₂-N₂O se comportó como la envolvente de un componente puro; las mezclas CO₂-CO y CO-N₂O pudieron ser predichas a concentraciones bajas de CO solamente y la envolvente binaria CO-SO₂ no pudo ser calculada a ninguna concentración de CO.

Al estudiar el comportamiento de las mezclas binarias, ternarias y cuaternarias predichas con la ecuación PSRK, los resultados indican que las mezclas que incluyen el CO en concentraciones elevadas hacen que el modelo diverja.

PC-SAFT

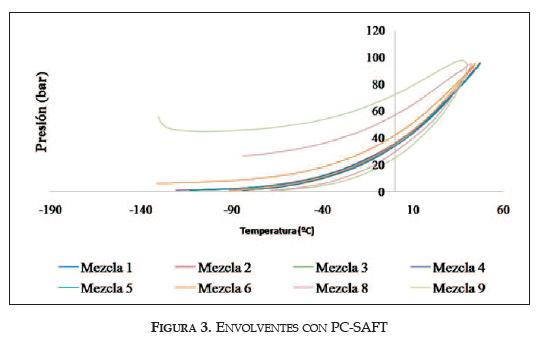
Al igual que con la ecuación PR, la ecuación PC-SAFT falla cuando las concentraciones de CO₂ son menores a 0,85. Las mezcla ternarias CO₂-CO-N₂O y CO₂-CO-SO₂ divergieron a concentraciones elevadas de CO, N₂O y SO₂. No fue posible predecir con este modelo la envolvente CO-N₂O-SO₂. El análisis de las mezclas binarias indicó los siguientes resultados: las mezclas CO-N₂O, CO₂-SO₂ y SO₂-N₂O pueden calcularse con el modelo en todo el rango de composiciones; la mezcla binaria CO₂-CO presenta una línea de rocío muy reducida a concentraciones elevadas de CO; la envolvente CO₂-N₂O, mostró superposición de las líneas de burbuja y de rocío, y para la envolvente CO-SO₂ a bajas concentraciones de CO no existe línea de rocío.

Observaciones finales

De acuerdo a los reportes consultados en la literatura [22], la información disponible experimental se centra en mezclas binarias de CO₂ con H₂O, N₂ o CH4. El mismo autor indica que no existen datos para mezclas binarias con NO_x, y que es bastante pobre la información de mezclas binarias de este componente con SO_x y CO.

Debido a la carencia de información, los resultados presentados en este trabajo no pueden ser comparados con datos experimentales. No obstante, la comparación de los tres modelos termodinámicos permite establecer algunas pautas de predicción. Por ejemplo, las mezclas de CO₂-CO-N₂O y CO₂-CO-SO₂ no pudieron predecirse con ninguna de las ecuaciones; la mayoría de las envolventes binarias pueden ser predichas con los modelos, teniendo como condición bajas concentraciones de CO. Ninguna ecuación permitió el cálculo de la envolvente de la mezcla CO-SO₂

Azeótropos

El análisis de las ecuaciones individuales indicó que todas predicen el mismo azeótropo binario CO₂-N₂O; el cambio de la composición azeotrópica con respecto a la presión se presenta en la figura 4. Como puede observarse en la fgura, el comportamiento del azeótropo cambia con el modelo termodinámico. La aplicación de la Ley de permite aclarar cuales azeótropos se consideran probables de existir.

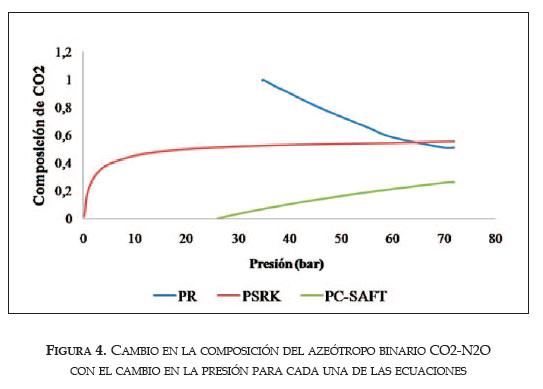
Las envolventes de fases calculadas con la ecuación PR indican que se presentan 4 azeótropos, 2 binarios (CO₂-N₂O y CO₂-CO) y 2 ternarios (CO₂-CO-N₂O, CO₂-N₂O-SO₂). Aplicando la Ley de Vresky se puede descartar tres de cuatro azeótropos, ya que no se cumplen las condiciones dadas por esta ley para su existencia. Uno de los azeótropos binarios no puede ser comprobado por la Ley de Vrsky, ya que a las condiciones que se presenta no se dispone del calor de vaporización de los componentes puros.

Las envolventes calculadas con la ecuación PSRK muestran la existencia de un solo azeótropo binario CO₂-N₂O, cuyo comportamiento es consistente con la Ley Vresky para la existencia de azeótropos.

El uso de la ecuación PC-SAFT para el cálculo de las envolventes indica que se presentan tres azeótropos: 1 binario (CO₂-N₂O), 1 terciario (CO2-CO-N2O) y 1 cuaternario (CO₂-CO-N₂O-SO₂). Los resultados indican que ninguno de los azeótropos puede ser analizado por la Ley de Vresky, debido a que no se dispone de las propiedades de los componentes puros a las condiciones en las que se presentan.

Con el análisis de la Ley de Vrevsky se pudieron descartar algunos azeótropos, pero no todos debido a la naturaleza del método, que permite aceptar o descartar el mismo azeótropo, dependiendo del modelo termodinámico empleado (el azeótropo binario CO₂-N₂O, mostrado en la figura 4, donde se demuestra que el comportamiento del azeótropo depende del modelo termodinámico, es un buen ejemplo de la afirmación dada).

Diagramas ternarios y determinación de regiones de destilación

Con la ecuación PR, partiendo de mezclas CO₂-CO-SO₂ y CO-N₂O-SO₂, toda composición conlleva a obtener por cima CO y por fondos SO₂. Para la mezcla CO-CO₂-N₂O, cuando la concentración de N₂O es mayor a la concentración del azeótropo, se obtiene N₂O por fondos y el azeótropo por la cima (a P=34,7). Para la mezcla CO₂-N₂O-SO₂, cuando la concentración de NO₂ es mayor a la del azeótropo, se obtiene la composición azeotrópica por la cima y SO₂ por fondos; cuando la concentración de N₂O es menor, se obtiene CO por cima y SO₂ por fondos.

En el caso de la ecuación PSRK, los resultados indican que para la mezcla CO₂-CO-N₂O, con concentraciones mayores de CO₂ a la azeotrópica, se obtiene por cima CO y por fondos CO₂; si la concentración de CO₂ es menor, se obtiene CO por cima y N₂O por fondos. Para las mezclas CO₂-CO-SO₂ y CO-N₂O-SO₂, para toda concentración de alimentación por cima se obtiene el azeótropo y por fondos SO₂. En el caso de CO₂-N₂O-SO₂ por cima se obtiene el azeótropo y por fondos SO₂.

Con la ecuación PC-SAFT, los resultados obtenidos indicaron que la mezcla CO₂-CO-N₂O no existiría, pues no se comporta como ninguno de los diagramas de Serafimov. La mezcla CO₂-CO-SO₂ permite obtener por cima CO₂ y por fondos SO₂. La mezcla CO-N₂O-SO₂ permite obtener por cima CO y por fondos SO₂. La mezcla CO₂-N₂O-SO₂, con concentraciones de N₂O mayores a las del azeótropo, permite que por cima se obtenga SO₂ y por fondos N₂O y cuando la concentración de N₂O es menor que la del azeótropo, se obtiene CO₂ por cima y SO₂ por fondos.

De acuerdo al análisis anterior, las condiciones a las cuales se analizará la separación (que favorezcan la obtención de CO₂) se enlistan en la tabla 3. Se escogen condiciones que deberían ser funcionales para probar la convergencia y la ejecución de cada ecuación.

Separación por destilación

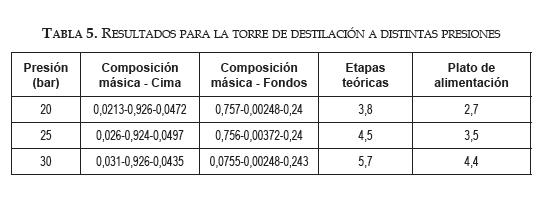
CO-CO₂-N₂O

Los resultados, los cuales se muestran en la tabla 5, muestran que a la misma relación de reflujo un cambio en 10 unidades de presión no afecta mayormente la distribución de los componentes y representa, en cambio, mayor cantidad de etapas, lo que aumentaría los costos de la torre.

CO-N₂O-SO₂ y CO₂-CO-SO₂

Para estas mezclas (con las ecuaciones PR y PC-SAFT, respectivamente) no se obtienen resultados en el rango de presiones para el cual se podía estimar (subcríticas) y para ninguna concentración inicial ensayada.

La exactitud y precisión de diseños predictivos de operaciones unitarias dependen de los modelos empleados en el cálculo de las propiedades básicas de las sustancias implicadas. Para el caso de la destilación, el cálculo del equilibrio de fases y de las envolventes de fases debe ser confable para poder diseñar correctamente la torre de destilación. En el presente trabajo se utilizaron tres modelos termodinámicos para el cálculo de las envolventes de fases de GEI y la predicción de la separación por destilación, de acuerdo al modelo termodinámico. Los resultados indican que las ecuaciones PR y PC-SAFT no fueron apropiadas para predecir el equilibrio de fases de GEI, ya que no se obtienen resultados consistentes tanto para los azeótrpos (analizados con la Ley de Vresky) ni para las condiciones de equilibrio (temperaturas y presiones muy superiores a las temperaturas y presiones críticas de los componentes puros). Debido a lo anterior, no fue posible analizar la separación por destilación con estas dos ecuaciones. En contraste, la ecuación PSRK predice el equilibrio y las envolventes en unos rangos de concentración, lo que permitió obtener un resultado de separación.

La concentración de CO se considera como uno de los factores determinantes en la predicción del equilibrio de fases, ya que a altas concentraciones de este componente todos los modelos comenzaron a divergir. Por lo tanto, otras ecuaciones deben ser exploradas para el cálculo del equilibrio de fases de estas mezclas. Es necesario encontrar el mejor modelo termodinámico para el cálculo de propiedades de GEI, ya que es la base para el diseño de procesos técnicos de mitigación y adaptabilidad, asociados a los fenómenos de calentamiento global y cambio climático.

[1] E. Kuntsi-Reunanen, "A comparison of Latin American energy-related CO2 emissions from 1970 to 2001," Energy Policy, vol. 35, pp. 586-596, 2007.         [ Links ]

[2] A. F. P. de Lucena, et al., "The vulnerability of renewable energy to climate change in Brazil," Energy Policy, vol. 37, pp. 879-889, 2009.         [ Links ]

[3] P. Christopher Zegras, "As if Kyoto mattered: The clean development mechanism and transportation," Energy Policy, vol. 35, pp. 5136-5150, 2007.         [ Links ]

[4] R. E. H. Sims, et al., "An overview of second generation biofuel technologies," Bioresource Technology, vol. 101, pp. 1570-1580, 2010.         [ Links ]

[5] J. A. Mathews, "Carbon-negative biofuels," Energy Policy, vol. 36, pp. 940-945, 2008.         [ Links ]

[6] S.-W. Park, et al., "Chemical kinetics of the reaction between carbon dioxide and phenyl glycidyl ether using Aliquat 336 as a catalyst," Catalysis Today, vol. 98, pp. 493-498, 2004.         [ Links ]

[7] S. W. Park, et al., "Reaction kinetic for poly(styrene-co-vinylbenzyl chloride)-supported catalyst containing pendant tetraethylammonium chloride in the reaction of glycidyl methacrylate with carbon dioxide," Catalysis Today, vol. 131, pp. 559-565, 2008.         [ Links ]

[8] D. C. Webster, "Cyclic carbonate functional polymers and their applications," Progress in Organic Coatings, vol. 47, pp. 77-86, 2003.         [ Links ]

[9] M. S. Zabaloy and J. H. Vera, "The Peng-Robinson Sequel. An Analysis of the Particulars of the Second and Third Generations," Industrial & Engineering Chemistry Research, vol. 37, pp. 1591-1597, 1998.         [ Links ]

[10] A. Grenner, et al., "Modeling phase equilibria of alkanols with the simplified PC-SAFT equation of state and generalized pure compound parameters," Fluid Phase Equilibria, vol. 258, pp. 83-94, 2007.         [ Links ]

[11] C. A. Cardona and L. G. Matallana, "Estudio del equilibrio de fases y curvas de residuos para el análisis de la estática en el proceso de obtención de diisopropil eter por destilación reactiva," NOOS, vol. 17, pp. 56-73, 2003.         [ Links ]

[12] P. C. W. Kwong et al., "Co-combustion performance of coal with rice husks and bamboo," Atmospheric Environment, vol. 41, pp. 7462-7472, 2007.         [ Links ]

[13] J. A. Quintero, et al., "Fuel ethanol production from sugarcane and corn: Comparative analysis for a Colombian case," Energy, vol. 33, pp. 385-399, 2008.         [ Links ]

[14] D.-Y. Peng and D. B. Robinson, "A New Two-Constant Equation of State," Industrial & Engineering Chemistry Fundamentals, vol. 15, pp. 59-64, 1976/02/01 1976.         [ Links ]

[15] S. Duque-Tobón and J. I. Carrero-Mantilla, "Una implementation abierta y generalizada del método predictivo de Soave-Redlich-Kwong para el cálculo de la constante de la ley de Henry," Ingeniería y Competitividad, vol. 10, pp. 9-28, 2008.         [ Links ]

[16] F. R. López, "Caracterización y validación dinámica de una Planta Piloto de Destilación," Maestría en ciencias, Departamento de Ingenería Electrónica Centro Nacional de Investigación y Desarrollo Tecnologico, Cuernavaca, 2008.         [ Links ]

[17] J. Gross and G. Sadowski, "Modeling Polymer Systems Using the Perturbed-Chain Statistical Associating Fluid Theory Equation of State," Industrial & Engineering Chemistry Research, vol. 41, pp. 1084-1093, 2001.         [ Links ]

[18] P. Arce and M. Aznar, "Modeling of critical lines and regions for binary and ternary mixtures using non-cubic and cubic equations of state," The Journal of Supercritical Fluids, vol. 42, pp. 1-26, 2007.         [ Links ]

[19] C. A. Cardona, et al., "Medición del equilibrio líquido-vapor del sistema metanol-acetato de metilo a 580 mmHg," Revista Colombiana de Química, vol. 35, pp. 19-27, 2006.         [ Links ]

[20] R. Reid, et al., The properties of gases and liquids, Fourth Edition ed.: McGraw Hill, 1987.         [ Links ]

[21] C. L. Yaws, The Yaws handbook of physical properties for hydrocarbons and chemicals: Physical properties for more than 41,000 organic and inorganic chemical compounds : coverage for C1 to C100 organics and Ac to Zr inorganics, Sixth edition ed. Houston: Gulf Pub Co., 2005.         [ Links ]

[22] N. Jacquemet, et al., "CO2 streams containing associated components—A review of the thermodynamic and geochemical properties and assessment of some reactive transport codes," Energy Procedia, vol. 1, pp. 3739-3746, 2009.         [ Links ]