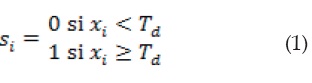Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y Desarrollo
versão impressa ISSN 0122-3461
Ing. Desarro. vol.31 no.2 Barranquilla jul./dez. 2013
ARTÍCULO DE INVESTIGACIÓN / RESEARCH ARTICLE
Datos sustitutos pseudoperiódicos en señales de voz para determinar dinámicas subyacentes
Pseudo-periodic surrogate data in speech signals to determine intrinsic dynamics
Edilson Delgado Trejos*
Instituto Tecnológico Metropolitano, ITM, (Colombia)
Juan Sebastián Hurtado Jaramillo**
Illinois Institute of Technology (USA)
Diego L. Guarín***
McGill University (Canadá)
Álvaro Á. Orozco****
Universidad Tecnológica de Pereira (Colombia)
*Investigador asociado al laboratorio MIRP, Facultad de Ingenierías, Instituto Tecnológico Metropolitano, ITM. Doctor en Ingeniería LI Automática, Universidad Nacional de Colombia. edilsondt@gmail.com
**Estudiante de la Maestría en Ingeniería Eléctrica, Illinois Institute of Technology (USA). Ingeniero Electricista, Universidad Tecnológica de Pereira (Colombia). jhurtado@hawk.iit.edu
***Estudiante del Doctorado en Ingeniería Biomédica, McGill University (Canadá). MSc Ingeniería Eléctrica, Universidad Tecnológica de Pereira (Colombia). diego.guarinlopez@mail.mcgill.ca
****Profesor Titular, Departamento de Ingeniería Eléctrica, Universidad Tecnológica de Pereira (Colombia). Doctor en Bioingeniería, Universidad Politécnica de Valencia (España). aaog@utp.edu.co
Correspondencia: Álvaro A. Orozco. Vereda la Julita, Campus Universidad Tecnológica de Pereira, Pereira, Risaralda (Colombia). Tel. +57 311 367 9667 – Fax +57 6 313 7122. Origen de subvenciones: Este artículo se presenta en el marco del proyecto de investigación PM10201, financiado por el Instituto Tecnológico Metropolitano, ITM, de Medellín y el proyecto de investigación 6-11-3, financiado por la Universidad Tecnológica de Pereira y Colciencias.
Fecha de recepción: 27 de febrero de 2013
Fecha de aceptación: 30 de abril de 2013
Resumen
Este artículo presenta las ventajas que tiene el método de los datos sustitutos pseudoperiódicos para determinar si existe algún tipo de dinámica en una señal adicional al comportamiento pseudoperiódico, i.e., correlaciones no lineales. Esto debido a que los métodos para detección de no linealidad clásicos solo pueden ser utilizados cuando la señal presenta un comportamiento aleatorio. Asimismo, se introducen la complejidad de Lempel-Ziv y la entropía muestral como estadísticas discriminantes para el desarrollo de una prueba de hipótesis. La primera está basada en el conteo de subsecuencias diferentes, mientras la segunda se basa en la medida de irregularidad de una señal. De acuerdo con esto, se propone una metodología efectiva aplicada al procesamiento de señales de voz usando la base de datos KayPENTAX. Los resultados experimentales mostraron que ambas estadísticas rechazaron la hipótesis bajo prueba, por lo tanto, fue posible concluir que existe algún otro tipo de dinámica en la señales de voz adicional a la dinámica pseudoperiódica. Particularmente, se encontró que la complejidad de Lempel-Ziv es útil a la hora de diferenciar entre señales con comportamientos dinámicos ligeramente diferentes.
Palabras clave: Complejidad Lempel-Ziv, Datos sustitutos pseudoperiódicos, Entropía muestral, Procesamiento de voz, Series de tiempo no lineales.
Abstract
This paper presents the advantages of a pseudo-periodic surrogate data method to determine whether there exists an additional dynamics (nonlinear correlations) in a pseudo-periodic time series, since classic surrogate data methods used to detect nonlinearity are limited to stochastic-like data. Likewise, Lempel-Ziv complexity and Sample Entropy are introduced as discriminating statistics for null hypothesis testing. The first is based on the counting of different sub-sequences in a time series while the latter is based on a measure of signal irregularity. According to this, an effective methodology is proposed for speech signal processing using the KayPEN-TAX database. Experimental results showed that both statistics are able to reject the null hypothesis for the signal under analysis. Therefore, it is possible to conclude that there is an additional dynamics in the speech signals other than the pseudo-periodic behavior. Particularly, it was found that the Lempel-Ziv complexity is able to differentiate between signals with slightly different dynamics.
Keywords: Lempel-Ziv complexity, Nonlinear time series, Pseudoperiodic surrogate data, Sample entropy, Speech signal processing.
1. INTRODUCCIÓN
Las señales de voz son series de tiempo que permiten representar gráficamente las ondas sonoras producidas por el aparato fonador humano y son usadas como refuerzo del diagnóstico asociado a la condición fisiológica del tracto vocal, proporcionando objetividad a la hora de emitir un juicio sobre la salud de la persona examinada [1]. Asimismo, estos registros han sido de gran utilidad para diferentes aplicaciones basadas en el procesamiento del habla [2]. Es importante resaltar que así como la mayoría de las señales fisiológicas, las señales de voz son de naturaleza dinámica, en tanto que presentan eventos transitorios, y en general, evidencian comportamiento no estacionario (i.e., los momentos estadísticos y su distribución de probabilidad dependen del tiempo) [1], [2].
Con el fin de contribuir al desarrollo de nuevas aplicaciones, ha crecido considerablemente el interés por extraer de las señales de voz conjuntos de características con alto nivel de representación. En este sentido, se han propuesto diversas técnicas de análisis, e.g., el análisis espectral [2], el análisis tiempo-frecuencia [3] y una de las técnicas más usadas, los Coeficientes Cepstrales en la Frecuencia Mel (MFCC) [4]. Cada una de estas técnicas tiene validez matemática y física, siempre y cuando su aplicación sea sobre señales que cumplan con ciertas restricciones específicas [5]. Por ejemplo, en el análisis espectral se asume que las series temporales son de naturaleza lineal y estacionaria, o que al menos lo son en la ventana de estudio. Si la serie bajo estudio no cumple con esta restricción, se obtendrá un espectrograma con falsos componentes de frecuencia y la interpretación de los resultados será probablemente incorrecta. De acuerdo con este planteamiento, es necesario e indispensable la implementación de procedimientos que permitan determinar el tipo de dinámica subyacente embebida en las series temporales, que para este caso son las señales de voz, con el fin de promover la aplicación de técnicas de procesamiento adecuadas a las propiedades particulares de las señales bajo estudio.
El método de los datos sustitutos se presenta como una estrategia para identificar la presencia de correlaciones no lineales en una serie temporal, esto con el fin de hallar información que soporte la estructuración adecuada de procesamiento y permita la construcción de espacios de representación capaces de capturar la dinámica intrínseca de la serie temporal [6].
El procedimiento para aplicar este método consiste en generar conjuntos de datos sustitutos (o artificiales) derivados de la serie temporal original, los cuales satisfacen alguna hipótesis, de manera que aunque compartan algunas propiedades con la serie original, no deben compartir la propiedad que está bajo prueba (e.g., si se desea probar la presencia de correlaciones no lineales es necesario asegurarse de que los datos sustitutos no posean dichas correlaciones sin importar si la serie original las tiene o no). Luego de aplicar alguna estadística discriminante, tanto a los datos originales como a los sustitutos, se debe hacer un análisis comparativo para determinar si la serie original no satisface la hipótesis planteada. Es importante resaltar que el objetivo no es aceptar las hipótesis, sino encontrar motivos suficientes para rechazarlas. Una explicación más detallada sobre el método de los datos sustitutos se encuentra en [7] y en las referencias allí contenidas.
Es fácil encontrar en la literatura ejemplos donde se hace un uso incorrecto del método de los datos sustitutos. Por ejemplo, en [8] se presenta una aplicación al procesamiento de señales de voz usando algoritmos planteados en [6] y algunas derivaciones introducidas en [9] y [10]. Estos algoritmos se basan en la presunción de que las señales (o por lo menos algunos segmentos de ellas) son estacionarias [11], lo cual por lo general no es cierto en el caso de las señales de voz. Por lo tanto, los resultados reportados en este tipo de estudios pueden ser incorrectos dado que no se respetan los prerrequisitos de los algoritmos. La consecuencia de esto es que se sugiere el uso de métodos que no necesariamente son apropiados para la señal que se está analizando. Por ejemplo, si la señal es no estacionaria, pero por alguna razón se utilizó un método inapropiado, se puede concluir que contiene dinámica no lineal, conduciendo a serios errores de análisis, puesto que las técnicas de análisis no lineal aplicadas a esta señal arrojarían resultados inválidos. Si por el contrario la serie de datos efectivamente posee correlaciones no lineales, pero estas nunca son detectadas, su análisis también se vería seriamente afectado, ya que los métodos lineales (los cuales son típicamente usados) no son capaces de extraer toda la información contenida en la señal.
En este artículose propone una modificación al método de losdatossustitutos propuesto en [12]. La hipotesis que se desea comprobar con este algoritmo es si existen componentes determinísticas en las señales de voz, además de la periodicidad inherente a los ritmos biológicos normales.
2. MATERIALES Y MÉTODOS
Base de datos
Para este estudio fue usada la base de datos KayPENTAX [13], creada en el Laboratoriode laVozy el Habla de MEEI (Massachusetts Eye andEar Infirmary). Esta base de datos contiene más de 1.400 muestras de voz, de aproximadamente 700 sujetos sanos y de pacientes con algún desorden patológico. Las grabaciones consisten en la pronunciación sostenida del fonema /ah/. Todas las muestras de voz fueron grabadas bajo condiciones controladas y preservando características de adquisición muy similares, específicamente, niveles de ruido ambiental muy reducidos, distancia entre el hablante y el micrófono constante, muestreo de 16-bits, acondicionamiento de señal robusto y frecuencia de muestreo de 25 kHz ó 50 kHz. En ese estudio solo se consideraron señales muestreadas a 25 kHz.
Datos sustitutos pseudoperiódicos (PPS)
Los datos sustitutos pseudoperiódicos (PPS por su acrónimo en inglés) se introdujeron para dar solución a las dificultades que se presentan al implementar el algoritmo de generación de datos sustitutos de ciclo truncado [12] (para mayor información sobre los datos sustitutos de ciclo truncado, ver [9] y [14]). El algoritmo PPS genera datos sustitutos que conservan las características deterministas de gran escala (tales como las tendencias periódicas), pero destruye las estructuras finas (como el determinismo lineal o no lineal) [15].
Para la generación de datos sustitutos pseudoperiódicos es necesario inferir la dinámica local por medio de la reconstrucción de un atractor y posteriormente contaminar las trayectorias de este atractor con rudio dinámico. En este sentido, los PPS siguen aproximadamente el mismo campo vectorial (o atractor) que la serie original, pero quedan contaminados con un ruido dinámico tal que se borra cualquier dinámica fina inmersa en la señal.
Formalmente, sea {xt} la serie temporal original de observaciones, y sea {zt} un vector de series de tiempo embebido en un espacio de estados {zt}, que puede ser construido aplicando un tiempo de retardo uniforme para el embebimiento  , donde la dimensión de embebimiento y el tiempo de retardo pueden estimarse por técnicas estándar, como vecinos más cercanos falsos (FNN) e información mutua promedio (AMI), respectivamente (ver [14] para más información al respecto). Posteriormente, se elige un punto del atractor como condición inicial T1 = Zj (1≤ j ≤ n-de τ + 1) y se establece un radio ρ, el cual depende de una probabilidad pi , que debe ser proporcionada por el usuario. A continuación se calcula la distancia entre T1 y todos los elementos del atractor. De manera aleatoria, se escoge un elemento zk , tal que
, donde la dimensión de embebimiento y el tiempo de retardo pueden estimarse por técnicas estándar, como vecinos más cercanos falsos (FNN) e información mutua promedio (AMI), respectivamente (ver [14] para más información al respecto). Posteriormente, se elige un punto del atractor como condición inicial T1 = Zj (1≤ j ≤ n-de τ + 1) y se establece un radio ρ, el cual depende de una probabilidad pi , que debe ser proporcionada por el usuario. A continuación se calcula la distancia entre T1 y todos los elementos del atractor. De manera aleatoria, se escoge un elemento zk , tal que  , y se asigna este elemento como el sucesor de T1 , i.e., T2=zk. Se continúa de la misma manera hasta que se forme un nuevo atractor {T1, T2,...Tn-deτ +1}. Finalmente, el vector de datos sustitutos está formado por los primeros componentes escalares de
, y se asigna este elemento como el sucesor de T1 , i.e., T2=zk. Se continúa de la misma manera hasta que se forme un nuevo atractor {T1, T2,...Tn-deτ +1}. Finalmente, el vector de datos sustitutos está formado por los primeros componentes escalares de  . Ver [11] para obtener información más detallada.
. Ver [11] para obtener información más detallada.
De acuerdo con el procedimiento anterior, además de que es necesaria una reconstrucción acertada del vector de tiempos de retardo, el éxito de este algoritmo depende del valor del parámetro . La selección correcta de este parámetro hace que las perturbaciones pequeñas introducidas destruyan la estructura microscópica determinista que se encuentra en los datos, dejando intactas las estructuras macroscópicas. El efecto se percibe cuando la serie original y los datos sustitutos queda con la misma forma básica (i.e., se conservan los patrones periódicos), pero cualquier escala fina de la dinámica determinista queda completamente destruida. Los datos sustitutos generados con el algoritmo PPS siempre serán realizaciones de una órbita periódica ruidosa con el mismo patrón periódico de los datos originales, siempre y cuando la elección de ρ sea la adecuada. Si ρ es muy pequeño (i.e., muy poca aleatorización), entonces los datos sustitutos y la señal original serán idénticos, o al menos muy parecidos. Por el contrario, si ρ es muy grande (i.e., demasiada aleatorización), entonces este algoritmo será equivalente al de un muestreo aleatorio. Con estas condiciones preestablecidas se hace necesario que la selección del valor de ρ sea en un punto de equilibrio entre estos dos extremos. En [16] se propone un procedimiento en el cual los valores de ρ son seleccionados en un rango amplio. Los resultados mostraron ser altamente consistentes para variaciones moderadas.
Complejidad de Lempel-Ziv (LZC)
La complejidad de Lempel-Ziv (LZC por su acrónimo en inglés) es una medida de complejidad no paramétrica basada en el número de subsecuencias diferentes que se presentan en la serie original y en la tasa de repetición de las mismas [17]. En [18] se menciona que: "Es una medida de complejidad en el sentido tanto estadístico como determinista y que en el contexto de señales fisiológicas, la LZC puede interpretarse como una medida de la variabilidad de los armónicos de la serie temporal. Esta medida está basada en la transformación de una señal a una secuencia cuyos elementos son un conjunto reducido de símbolos". Gómez Peña [18] describe que el método de conversión consiste en transformar el registro de estudio en una secuencia binaria. Para ello se compara la serie temporal con un umbral Td, que por lo general es la mediana, puesto que es más robusta a datos espurios que la media. Así, la señal original x=(x1,x2,... xn) se transforma en una secuencia binaria p=(s1,s2,...sN), donde:
Adicionalmente, se tiene que un contador de complejidad c(N) mide el número de patrones distintos contenidos en la secuencia. Así, una secuencia p=(s1,s2,...sN), donde s1,s2,...sN son caracteres, es analizada de izquierda a derecha y el contador de complejidad c(N) se incrementa una unidad cada vez que encuentra una nueva subsecuencia de caracteres en el proceso de análisis. Después de una normalización, la medida de la complejidad refleja la tasa de nuevos patrones. El algoritmo para el cálculo de la complejidad y una discusión más detallada se pueden encontrar en [18].
Entropía muestral
Inicialmente, Pincus [19] introdujo la entropía aproximada (ApEn por su acrónimo en inglés) como una medida para cuantificar la regularidad de una serie de datos, incluso cuando son ruidosos y de corta longitud. Se asigna una ApEn pequeña cuando la serie contiene patrones repetitivos, mientras la irregularidad incrementa su valor. El algoritmo compara la distancia entre vectores y cuenta el número de aquellos que no superan una distancia predeterminada, apareciendo un sesgo que hace la ApEn altamente dependiente de la longitud de la serie analizada. Para reducir este sesgo se introdujo la entropía muestral (SampEn por su acrónimo en inglés) [20], donde valores grandes se asocian a una alta irregularidad y valores pequeños a la notable regularidad. Gómez Peña [18] menciona que:
"Antes de calcular la SampEn hay que fijar dos parámetros: la longitud m, que determina el tamaño de los vectores comparados, y una ventana de tolerancia r, que suele ser normalizada usando la desviación estándar de la serie original". Estos dos valores pueden afectar seriamente los resultados del cálculo de la SampEn. Han sido sugeridos algunos valores y métodos para su selección [18], [19]. El procedimiento para el cálculo de la SampEn y una discusión más detallada se pueden revisar en [18].
Metodología propuesta para señales de voz
Se propone la siguiente metodología para establecer la existencia de determinismo no lineal en señales de voz. Se toma en cuenta la naturaleza no estacionaria y pseudoperiódica de este tipo de series de tiempo fisiológicas, y se emplean la complejidad de Lempel-Ziv (LZC) y la entropía muestral (SampEn) como estadísticas discriminantes.
▪ Señales originales para el estudio
De la base de datos KayPENTAX se seleccionaron, de manera aleatoria, diez registros (cinco mujeres y cinco hombres) de sujetos sin ninguna patología al pronunciar el fonema /ah/ y muestreados a 25 kHz. Para efectos de este artículo, las señales seleccionadas son suficientes, dado que el método analiza una señal contra sí misma y no su relación con otras, es decir, la confiabilidad estadística no depende del número de señales originales sino del número de datos sustitutos.
▪ Preproceso
Las señales de voz son preprocesadas de la siguiente manera: cada una debe tener un número entero de ciclos, se elimina la diferencia entre puntos extremos y finalmente se normaliza la señal eliminando su media y haciendo que la desviación estándar sea igual a la unidad.
▪ Generación de datos sustitutos pseudoperiódicos
Como el método de los datos sustitutos de ciclo truncado no es adecuado para las señales de voz correspondientes a un fonema vocálico por sus pseudoperiodicidades, se usa el algoritmo PPScomo una posible mejor alternativa.
Sin embargo, hay que tener en cuenta que el éxito de este método radica en una elección adecuada del valor del radio de ruido ρ. Por este motivo se sigue la metodología de construcción de datos sustitutos pseudoperiódicos presentada en [16], donde se proponen nueve valores diferentes de ρ (i.e., diferentes intensidades de ruido) para cada una de las señales.
El radio de ruido depende no solo de las características de la señal, sino de una probabilidad que puede ser definida por el usuario. El método consiste entonces en utilizar nueve diferentes probabilidades (desde 0. 1 hasta 0.9) y de esta manera obtener nueve radios distintos. Dado que la capacidad de discriminación del algoritmo está ligada al número de datos sustitutos utilizados, se propone entonces generar 50 de estas series por cada ρ obtenido. Así, se observa la relación entre los datos originales y los construidos artificialmente para una cierta probabilidad (nivel de aleatorización) y se revelan las tendencias cambiantes de la complejidad.
▪ Estadísticas discriminantes
Para emplear la LZC y la SampEn como estadísticas discriminantes se propone calcularlas para las señales de voz y para los sustitutos generados. Particularmente, en [18] se demuestra que el valor adecuado para fijar los parámetros de estimación de la SampEn son m = 2 y r = 0. 25 veces la desviación estándar de la serie de datos original.
▪ Prueba de hipótesis
De cada una de las señales originales se generan señales sustitutas utilizando el algoritmo PPS. La hipótesis nula se enuncia como: No hay otro determinismo más que el comportamiento pseudoperiódico, i.e., una órbita periódica con ruido no correlacionado. La prueba de hipotesis para una señal se realiza de la siguiente manera (ver figura 1): se toma la serie original con sus respectivas señales sustitutas y se calculan en ellas las estadísticas discriminantes, LZC y SampEn, para luego verificar si el valor obtenido de la señal original hace parte de las colas de la función de distribución de probabilidad construida con los valores obtenidos de las señales sustitutas. Si el valor está en las colas, con un nivel de confianza del 95%, se rechaza la hipótesis nula para esa señal en particular. Esto mismo se hace con cada una de las señales originales.
3. RESULTADOS Y DISCUSIÓN Datos sustitutos pseudoperiódicos
Los valores obtenidos para la dimensión de embebimiento (de) y el tiempo de retardo (τ) involucrados en la reconstrucción del atractor en el espacio de estados para cada una de las señales de voz se muestran en la tabla 1.
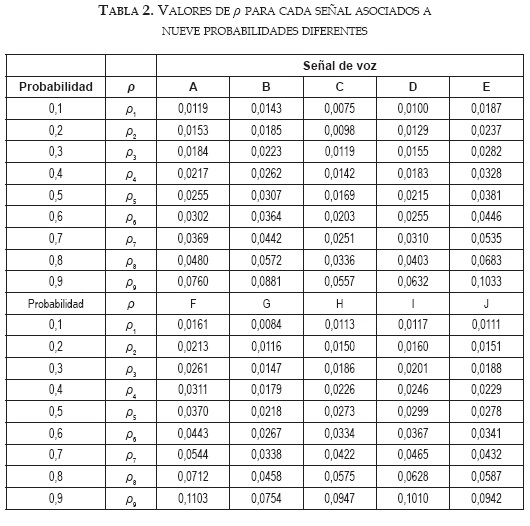
Asimismo, en la tabla 2 se observan los diferentes valores de ρ para las diez señales de voz analizadas, empleando los parámetros expuestos en la tabla 1. Con los valores reportados en las tablas 1 y 2 se construyeron los datos sustitutos ejecutando el algoritmo PPS.
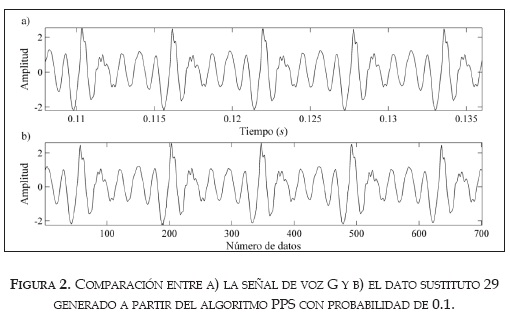
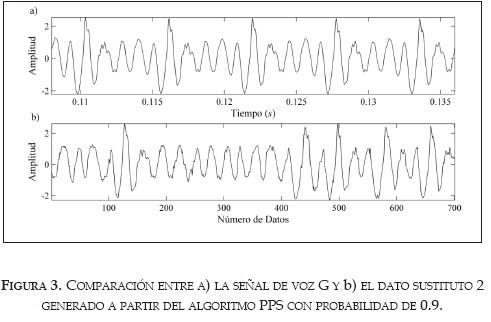
En la figura 2 se observa que los datos sustitutos para la señal G, generados por probabilidades bajas (≈0.1), son muy similares a la serie original, a diferencia de los generados con probabilidades altas (≈0.9), mostrados en la figura 3.
Los datos sustitutos generados a partir de probabilidades pequeñas contienen formas de onda repetidas, ya que estos sustitutos saltan de una trayectoria a otra en el espacio de estados (i.e., ellos pueden seguir una trayectoria completa y luego repetir parte de la trayectoria nuevamente). Por este motivo, los datos sustitutos construidos por medio de probabilidades pequeñas contienen periodicidades de largo plazo. Con el aumento de la probabilidad (incremento en el ruido) los datos sustitutos saltan más frecuentemente entre diferentes trayectorias con menos repeticiones. Así, la complejidad de los datos sustitutos con probabilidades de a se asemeja más a la complejidad de la señal original, puesto que imitan toda la dinámica de los interciclos. Por el contrario, si la probabilidad (el ruido) es demasiado grande, entonces los datos sustitutos son equivalentes a tener una señal de ruido independiente e idénticamente distribuida.
Complejidad de Lempel-Ziv y entropía muestral como estadísticas discriminantes
La figura 4 muestra laprobabilidad dequela SampEn calculada para laseñal original esté en las colas de la distribución de los datos sustitutos. Si esta probabilidades mayor que el 5%, entonces no es posible rechazar la hipótesis con el nivel de confianza seleccionado en el este estudio. Por el contrario, si la probabilidad es menor que el 5%, es posible rechazar la hipótesis. Es posible observar en la figura 4 que para probabilidades pequeñas (lo cual se traduce directamente en radios de ruido pequeños i.e., ρ1, ρ2 y ρ3) no es posible rechazar la hipótesis nula para algunas de las señales, pero como se discutió anteriormente, los resultados con probabilidades pequeñas no son los más adecuados para rechazar o no rechazar la hipótesis nula debido al parecido que tienen los datos sustitutos con la señal original. Por lo tanto, es mejor no considerar estos valores de ρ y tomar los resultados obtenidos con las demás probabilidades.
Es posible observar en la figura 4 que para probabilidades mayores que 0.3 es posible rechazar la hipótesis nula planteada con todas las señales. En la figura 5 se observa que utilizando la complejidad de Lempel-Ziv como estadística discriminante se encontraron resultados similares, aunque en esta ocasión la hipótesis nula pudo ser rechazada para todos los valores de ρ .
4. CONCLUSIONES
Este artículo presenta una metodología efectiva para evaluar el determinismo no lineal de señales fisiológicas con naturaleza pseudoperiódica. Se resuelve el inconveniente que tienen algoritmos muy populares en la literatura respecto a la suposición de que la señal de estudio es aleatoria, o algunas veces estacionaria, lo cual es inadmisible para las señales de voz. Esta metodología se basa en el algoritmo PPS para la generación de datos sustitutos y las estadísticas LZC y SampEn para la verificación de la hipótesis nula: "no hay otro determinismo más que el comportamiento pseudoperiódico". No obstante, los problemas relacionados con la selección del radio de ruido ρ exigen el cálculo de una gran cantidad de parámetros antes de la generación de los datos sustitutos, lo cual hace que el método conlleve un ligero pero apreciable costo computacional.
De acuerdo con los resultados experimentales,se comprueba que el procedimiento para determinar la presencia de estructuras no lineales en conjuntos reales de datos, donde la dinámica subyacente no siempre puede ser preestablecida, requiere el uso de diferentes estadísticas discriminantes, dado que algunos sistemas de prueba llegan a ser robustos a la prueba estadística. En particular, mientras la estadística discriminante LZC permite rechazar la hipótesis nula determinantemente, la SampEn no permite ese rechazo si el sistema de prueba no se ejecuta de la manera correcta.
Como valor agregado a este estudio, se pudo comprobar que la estadística discriminante LZC captura la dinámica subyacente y no lineal contenida en las señales de voz, de manera que el proceso de datos sustitutos destruyó claramente esta información, a pesar de conservar la naturaleza pseudoperiódica y, por ende, la hipótesis nula fue rechazada de forma absoluta. Sin embargo, la estadística discriminante SampEn resultó no ser la más adecuada para el estudio de determinismo no lineal en señales de voz, puesto que la información quedó embebida en el comportamiento pseudoperiódico, y esto no permitió una discriminación clara entre los datos sustitutos y la señal real.
Así, se muestra que si bien la señales de voz tienen determinismo no lineal, la evaluación exige ser más exhaustiva por su naturaleza pseudoperiódica y no estacionaria, determinando también los parámetros que capturan la dinámica subyacente y no lineal de los datos. La prueba con señales pertenecientes a dos clases diferentes (normal y patológica) permitió mostrar que el método propuesto es consistente respecto al hallazgo de estructuras provocadas por el operador no lineal aun cuando las señales contienen trastornos patológicos.
Agradecimientos
Se agradece a la Universidad Tecnológica de Pereira, Colciencias y el Instituto Tecnológico Metropolitano (ITM) de Medellín por financiar esta investigación.
REFERENCIAS
[1] R. Rangayyan, Biomedical Signal Analysis: A Case-Study Approach, New York: IEEE Press, 2002. [ Links ]
[2] J. R. Deller Jr., J. H. L. Hansen, and J. G. Proakis, J. G., Discrete-Time Processing of Speech Signals, Piscataway: IEEE Press, 2000. [ Links ]
[3] R. Chiodi and D, Massicotte, "Voice activity detection based on wavelet packet transform in communication nonlinear channel," in 1st International Conference on Advances in Satellite and Space Communications, Colmar, France, pp. 54-57, 2009. [ Links ]
[4] L. S. Chee, O. C. Ai, M. Hariharan, and S. Yaacob, "MFCC based recognition of repetitions and prolongations in stuttered speech using k-NN and LDA," in IEEE Student Conference on Research and Development, UPM Serdang, Malaysia, pp. 146-149, 2009. [ Links ]
[5] N. Huang and N. O. Attoh-Okine, The Hilbert-Huang Transform in Engineering, Boca Raton: Taylor & Francis Group, 2005. [ Links ]
[6] J. Theiler, S. Eubank, A. Longtin, B. Galdrikian, and D. Farmer, "Testing for nonlinearity in time series: The method of surrogate data," Physica D: Nonlinear Phenomena, vol. 58, pp. 77-94, 1992. [ Links ]
[7] D. L. Guarín, C. H. Rodríguez, and Á. Á. Orozco, "Pruebas de no linealidad: el método de los datos sustitutos," Scientia et Technica, vol. 44, pp. 292-297, 2010. [ Links ]
[8] M. Small, C. K. Tse, and T. Ikeguchi, "Chaotic dynamics and simulation of Japanese vowel sounds," in Proceedings of the European Conference on Circuit Theory and Design, Cork, Ireland, pp. 169-172, 2005. [ Links ]
[9] J. Theiler, "On the evidence for low-dimensional chaos in an epileptic electroencephalogram," Physics Letters A, vol. 196, pp. 335-341, 1995. [ Links ]
[10] T. Schreiber and A. Schmitz, "Improved surrogate data for nonlinearity tests," Physical Review Letters, vol. 77, pp. 635-638, 1996. [ Links ]
[11] M. Small, T. Nakamura, and X. Luo, "Surrogate data methods for data that isn't linear noise," in Nonlinear Phenomena Research Perspectives, C W. Wang, Ed. New York: Nova Sicence, 2007. [ Links ]
[12] M. Small, D. Yu, and R. G. Harrison, "Surrogate test for pseudoperiodic time series data," Physical Review Letters, vol. 87, pp. 188101, 2001. [ Links ]
[13] KayPENTAX, "Disordered voice database and program, Model 4337," Available at: http://www.kayelemetrics.com/. [ Links ]
[14] M. Small, Applied Nonlinear Time Series Analysis: Applications in Physics, Physiology and Finance, Singapore: World Scientific Publishing, 2005. [ Links ]
[15] M. Small and C. K. Tse, "Applying the method of surrogate data to cyclic time series," Physica D, vol. 164, pp. 187-201, 2002. [ Links ]
[16] Y. Zhao, S. Junfeng, and M. Small, "Evidence consistent with deterministic chaos in human cardiac data: Surrogate and nonlinear dynamical modeling," International Journal of Bifurcation and Chaos, vol. 18, pp. 141-160, 2008. [ Links ]
[17] A. Lempel and J. Ziv, "On the complexity of finite sequences," IEEE Transactions on Information Theory, vol. 22, pp. 75-81, 1976. [ Links ]
[18] C. Gómez Peña, "Análisis no lineal de registros magnetoencefalográficos para la ayuda en el diagnóstico de la enfermedad de Alzheimer," Tesis Doctoral dirigida por R. Hornero Sánchez, Departamento de Teoría de la Señal y Comunicaciones e Ingeniería Telemática, Universidad de Valladolid, 2009. [ Links ]
[19] S. M. Pincus, "Approximate entropy as a measure of system complexity," Proceedings of the National Academy of Sciences of the United States of America, vol. 88, pp. 2297-2301. [ Links ]
[20] J. S. Richman and J. R. Moorman, "Physiological time-series analysis using approximate entropy and sample entropy," American Journal of Physiology - Heart and Circulatory Physiology, vol. 278, pp. H2039-H2049, 2000. [ Links ]