Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383
C.T.F Cienc. Tecnol. Futuro vol.5 no.2 Bucaramanga Jan./June 2013
COMPUTATIONAL TOOL FOR MATERIAL BALANCES CONTROL IN NATURAL GAS DISTRIBUTION NETWORK
HERRAMIENTA COMPUTACIONAL PARA EL CONTROL DE BALANCES DE MASA EN LAS REDES DE DISTRIBUCIÓN DE GAS NATURAL
Jesús-David Badillo-Herrera1*, Arlex Chaves2 and José-Augusto Fuentes-Osorio1
1Corporación Centro de Desarrollo Tecnológico de GAS, Piedecuesta, Santander, Colombia 2Universidad Industrial de Santander, Bucaramanga, Santander, Colombia
e-mail: jbadillo@cdtdegas.com
(Received: May 29, 2012; Accepted: Apr. 24, 2013)
* To whom correspondence should be addressed
ABSTRACT
In natural gas industry, measurement of process variables allows to assess the quantity and quality of commercialized gas. Nevertheless, since errors, gross and random are always present in measurements, mass and energy balances are not satisfied. This situation leads natural gas distribution companies into invoicing issues. In this paper, a computational tool is proposed, which guarantees that the law of conservation of mass is obeyed by decreasing random error effects and detecting systematic deviations in the measurement equipment (gross errors). This tool is based on Data Reconciliation (DR) and Gross Error Detection (GED) techniques. Different DR and GED methodologies were studied by means of assessment of their advantages and disadvantages. Non-conventional DR and GED methods are proposed as part of the developed tool in order to obtain accurate reconciled results in cases of difficult gross error detections on natural gas distribution systems. The tool was validated by a typical literature problem, and it was then applied to a natural gas distribution network. Results were in agreement with reports of failures of some instruments.
Keywords: Random errors, Gross errors, Data reconciliation.
RESUMEN
En la industria del gas natural, la medición de las variables de procesos permite conocer la cantidad y calidad de gas comercializado. No obstante, todas las mediciones presentan errores que generan el incumplimiento de los balances de masa y energía, ocasionando inconvenientes en los procesos de facturación de las empresas distribuidoras de gas natural. En este artículo, se propone el desarrollo de una herramienta computacional que asegure el cumplimiento de la ley de conservación de la masa, a través de la disminución del efecto de los errores aleatorios y de la detección de fallas o factores, como fugas, venteos, etc., que generen desviaciones sistemáticas (errores gruesos) en los sistemas de medición. Esta herramienta está basada en las técnicas de Reconciliación de Datos (DR, por sus siglas en inglés) y Detección de Errores Gruesos (GED, por sus siglas en inglés). Con tal fin, se llevó a cabo un estudio y selección de las diferentes metodologías de DR y GED, evaluando las ventajas y limitaciones que cada una de estas presenta. Por otro lado, métodos no convencionales de DR y GED son propuestos para ser usados en casos de difícil detección de errores gruesos con el fin de evitar reconciliados erróneos. La herramienta fue validada con problemas típicos encontrados en la literatura, y luego fue aplicada a una red de distribución real, para posteriormente discutirse los resultados obtenidos. Los resultados de la reconciliación de datos fueron concordantes con los reportes de fallas de algunos sistemas de medición.
Palabras clave: Errores gruesos, Errores aleatorios, Reconciliación de datos.
RESUMO
La indústria do gás natural, a medição das variáveis de processos permite conhecer a quantidade e a qualidade do gás comercializado. Porém, todas as medições apresentam erros que geram o descumprimento dos balanços de massa e de energia, ocasionando inconvenientes nos processos de faturamento das empresas distribuidoras de gás natural. Neste artigo, propõe-se o desenvolvimento de uma ferramenta computacional que garanta o cumprimento da lei de conservação da massa, através da diminuição do efeito dos erros aleatórios e da detecção de falhas ou fatores, como fugas, venteios, etc., que geram desvios sistemáticos (erros grossos) nos sistemas de medição. Esta ferramenta está baseada nas técnicas de Reconciliação de Dados (DR, por sua sigla em inglês) e Detecção de Erros Grossos (GED, por sua sigla em inglês). Com esta finalidade, foi realizado um estudo e seleção das diferentes metodologias de DR e de GED, avaliando as vantagens e limitações que cada uma destas apresenta. Por outro lado, métodos não convencionais de DR e de GED são propostos para serem usados em casos de difícil detecção de erros grossos com a finalidade de evitar reconciliados errôneos. A ferramenta foi validada com problemas típicos encontrados na literatura e, logo foi aplicada a uma rede de distribuição real, para posteriormente discutirem-se os resultados obtidos. Os resultados da reconciliação de dados estiveram de acordo com os relatórios de falhas de alguns sistemas de medição.
Palavras-chave: Erros Grossos, Erros Aleatórios, Reconciliação de dados.
1. INTRODUCTION
Measurements of process variables in natural gas industry, such as volume, composition, pressure, temperature and calorific value, are unquestionably important in natural gas industries because these variables allow calculating the quantity and quality of commercialized gas. Considering how relevant these measurements are, accurate information of such variables is imperative for natural gas distribution companies. Nevertheless, every measurement contains errors caused by different sources, for instance, noises, systematic deviation in measurement instrument, changes in environmental conditions etc. (Bagajewicz, 2010). Such errors make mass and energy balances not satisfied, which hinders invoicing processes of natural gas distribution companies. As a result, legal issues and revenue losses could occur. This situation gets worse if there are leakages or illegal connections in the pipeline systems.
However, accomplishment of constraints imposed by mass and energy conservation laws can be achieved by numerical and statistical techniques, such as Data Reconciliation (DR) and Gross Errors Detection (GED) (Bagajewicz, 2010; Narasimhan & Jordache, 2000). DR is a statistical technique which improves precision in measured data by means of reducing random errors and adjusting measurements according to material balance, energy balance and standard deviations of each variable (Narasimhan & Jordache, 2000). Nevertheless, some errors caused by nonrandom events, e.g. failure of measurement systems, can produce inaccurate reconciled results. Such errors are called gross errors. In order to avoid this phenomenon, GED techniques are used to identify, locate and -if possible- estimate gross error sizes to obtain better adjustments (Crowe, 1996; Bagajewicz, 2010).
Various important contributions in DR and GED areas have been published since the first DR problem formulation was posed. Kuehn and Davidson (1961), who first introduced the DR problem in 1961, derived an analytical solution for a linear steady-state material balance by Lagrange multipliers, in a case where all variables were measured. Another important contribution was made by Mah, Stanley and Downingin (1976). They solved the general linear DR problem but, unlike Kuehn and Davidson (1961), Mah et al. (1976) considered the estimation of unmeasured variables and GED problem caused by leakage and biases in meters. This work also shows, by means of the simulation of a refinery process, that DR improves the accuracy of measured variables when sufficient redundancy exists.
Several authors have attempted to apply DR techniques on natural gas distribution systems. Heenan, Cardiel, and Serth (1987) researched the feasibility of applying DR and GED techniques on natural gas distribution networks, with the purpose of resolving unaccounted gas issues. In their work, they found some restrictions due to the small redundancy degree of these systems. Consequently, Heenan et al. (1987) proposed to install additional meters in order to increase it. Nonetheless, this means that significant investments would be required, whereby their solution is not feasible for most of natural gas distribution companies. On the other hand, Bagajewicz and Cabrera (2003) proposed a methodology based on mass and mechanical energy balances to increase redundancy degree in natural gas pipeline systems without significant changes in computational time. Nevertheless, their simplified model needs to be corrected by additional modular software (PRO II); hence, the methodology becomes impractical. Moreover, Bagajewicz and Cabrera (2003) did not take into account GED problems in their contribution. Finally, Oliveira and Aguiar (2009) showed analytical applications of DR techniques on the natural gas industry. They applied DR techniques in different cases studies, such as resolving disputes between supplier and consumer, equipment diagnosis, characterization study of methane and homogeneity study in terms of density. Their work demonstrated how convenient and useful DR techniques are in natural gas applications.
Taking into consideration the benefits of DR and GED, a computational tool based on these techniques is proposed. This tool improves the quality of measured flow on natural gas distribution systems and, unlike previous works, it attempts to identify possible meters affected by gross errors in order to obtain accurate reconciled results. DR and GED limitations on natural gas distributions networks were treated by usage of alternative methods which are applied in specific cases of difficult GED. Implementation of additional measurement systems and modular software were avoided, as well as excessive investments.
2. THEORETICAL DEVELOPMENT
Data Reconciliation Methods
DR is a technique which makes unique estimations of conflictive measurements by adjusting them according to model restrictions. These models are usually linear mass balances (Crowe, 1996; Bagajewicz, 2010). Furthermore, DR is based on redundancy property of variables, where a measured variable is redundant if it can be calculated, at least in one way, by remaining variables and process constraints (Bagajewicz, 2010; Crowe, 1996).
Mathematically, DR is accomplished by minimizing the following objective function:

In the Equation 1, ρ is a function which can change according to assumptions related to error behavior (Özyurt & Pike, 2004), where error equals (yi- xi/σi); yi is the estimated reconciled value, xi is measured variable, si is the standard deviation and n is the number of measured variables.
Where, MT is the transpose of the incidence matrix system, SR represents the measurement error covariance matrix, I is the identity matrix and X is the vector of
As it was already mentioned above, Equation 1 is subjected to constraints imposed by linear mass balances. These restrictions are described by the following expression:

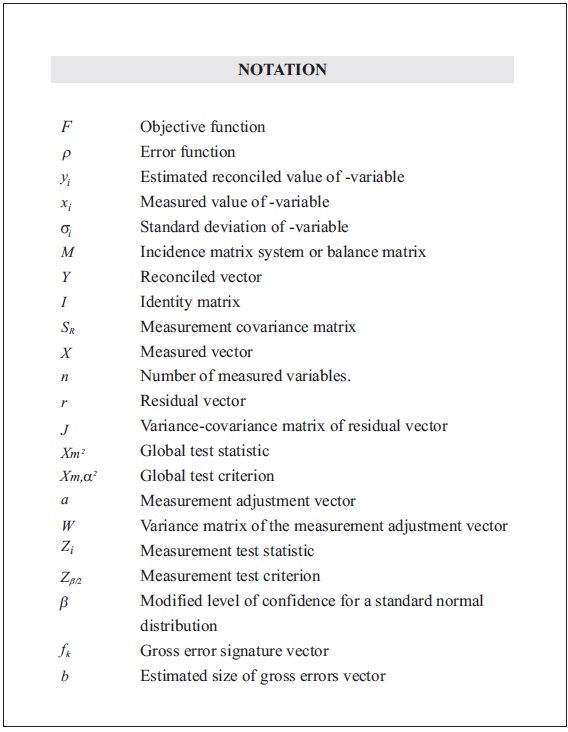
Where, M is the incidence matrix system (balance matrix) and Y is the vector of reconciled.
Conventional DR defines ρ as a least square function; consequently, Equation 1 is transformed into:

This DR problem has a matricial analytical solution, obtained by Lagrange multipliers method. This solution is:
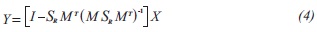
Where, MT is the transpose of the incidence matrix system, SR represents the measurement error covariance matrix, I is the identity matrix and X is the vector of measured variables (Bagajewicz, 2010; Narasimhan & Jordache, 2000).
Even when the least-squares objective function allows obtaining quick results because of its analytical solution, reconciled values obtained by this method could be erroneous. Least square objective function assumes measurement errors from a normal distribution, which mean is equal to zero; therefore, if data contain gross errors, reconciled results could be inappropriately set. This phenomenon is known as smearing effect (Crowe, 1996; Özyurt & Pike, 2004).
Other objective functions have been proposed in order to improve reconciled results when a gross error is not identified. Özyurt and Pike (2004) stated that better results can be obtained from heavy-tailed distribution functions, such as cauchy distribution, contaminated normal distribution, Lorentzian distribution and fair distribution, advocating that such distributions account for the smearing effect caused by gross errors. The objective functions were derived from the distribution by maximum likelihood method: This development resembles to Gauss's procedure, used to obtain the leasts quares objective function from the standard normal distribution function for residuals. Additionally, Özyurt and Pike (2004) assessed these functions in different literature and industrial cases. Their results indicate that Cauchy function Equation 5 yields the best reconciled results; however, computational time could increase significantly because of nonlinearity of this function, as can be observed from the following expression (Özyurt & Pike, 2004):
Gross Error Detection (GED)
Basic Gross Error Techniques
As it was already mentioned, DR techniques assume that only random errors can be present in the data. Accurate and feasible reconciled estimations cannot be obtained in the presence of gross errors, thus they must be identified, estimated or eliminated from the set of data before to get final results.
The basic techniques of GED are based on Hypothesis Testing theory (Bagajewicz, 2010). These methods decide whether gross errors are present in the data or not by evaluating the deviation of the test statistics in relation to the critical value. Furthermore, these techniques exploit the previously described redundancy property.
Several basic tests can be used in order to identify gross errors in the data. One of the most widely used tests is the Global Test (GT) (Narasimhan & Jordache, 2000). This test cannot identify which variable contains the gross error, but provides a list of suspicious ones. GT attempts to identify gross errors in measurements from an analysis of the residual vector (r), where r is defined as the cartesian product of the incidence matrix system, M and the vector of measured variables X, i.e. r = M·X. The variance-covariance matrix of residual vector, J is given by:

If there are not gross errors, r vector follows a normal distribution which mean is zero. Xm2 from Equation 7 follows a Chi-squared distribution with m degrees of freedom. m is the number of rows of the balance matrix.

The test criterion is the critical value of Chi-squared distribution (?m,a2), with m degrees of freedom at significance level α, which equals 95%. Hence, if Xm2 is greater than Xm,α2, at least one gross error is detected in the measurements (Bagajewicz, 2010; Narasimhan & Jordache, 2000).
Another widely used test is the Measurement Test (MT). This test, unlike GT, identifies which specific variable contains the gross error. MT is based on the measurement adjustment vector a, which is defined as the difference between the measured vector (X) and the reconciled vector (Y) (Mei, Su & Chu, 2006). The variance of the measurement adjustment vector, W, is given by:

If data do not contain gross errors, then α follows a normal distribution with zero mean. Zi is the statistic test (Equation 9) and follows a standard normal distribution in lack of gross errors.

In this test, the criterion is Zβ/2 and is defined as the critical value of standard normal distribution for a modified level of confidence β, where

In Equation 10, n is the number of columns of balance matrix (M). If Zi is greater than Zβ/2, measurement i is suspicious of containing a gross error.
There are others non-conventional methods for gross errors detection. One of them is the X84 technique. This method was posed by Fusiello, Trucco, Tommasini and Roberto (1999) and it is based on robust statistic methods, which is a field of statistics that produces accurate statistical estimators, not affected by outliers (Özyurt & Pike, 2004). The X84 method detects gross errors when the difference between the measured and reconciled value, known as residual, is greater than k times the median deviation (Özyurt & Pike, 2004).
Multiple Gross Errors Identification Strategies
Basic tests can only detect a single gross error in the data; thus, when there are multiple gross errors, an additional strategy is necessary to obtain correct identification and location of all gross errors. These strategies can be classified as either simultaneous strategies or serial strategies. The latter in turn can be classified either as elimination strategies or compensation strategies.
In this paper, a compensation serial strategy known as Serial Identification with Collective Compensation (SICC) was used. This strategy was proposed by Jiang and Bagajewicz in (1999). SICC uses MT in order to identify suspicious gross errors in measurements. Then, SICC estimates the identified gross errors and adds it to the suspicious measurement. As subsequent gross errors are identified, their sizes are simultaneously recalculated and added to the detected measurement at each step, until none gross error is detected.
The SICC has several advantages in comparison with other multiple gross errors identification strategies. First of all, SICC avoids wrong estimates of the identified gross errors, since they are recalculated at each stage. Secondly, SICC detection capacity does not decrease when there are few errors, unlike the Unbiased Estimated Technique (UBET), proposed by Rollins and Davis (1992) (Narasimhan & Jordache, 2000). Finally, the SICC method keeps the redundancy degree of the system, unlike elimination strategies (Narasimhan & Jordache, 2000), which guarantees a better performance of DR techniques.
Gross Error Size Estimation
As it was already mentioned, it is desirable to have information related to gross error size for production accounting. Furthermore, gross error sizes can be used in DR to compensate suspicious measurements, instead of eliminating them, which allows keeping the redundancy degree of the system. Herein, error size estimation formula developed by Narasimhan and Mah (1987) is used. This formula considers gross errors, both bias and leakage, as a part of the restriction model.
Let ej be a nx1 vector with value 1 in position j (position of the gross error located by MT) and zero elsewhere. This vector is related to bias of the measurements. The leakage vector is not considered here.
Narasimhan and Mah (1987) defined the gross error signatures vector (fk) equals both biases and leakage vectors. Since process leaks are neglected in this work, gross error signatures vector is mathematically defined as follows:

This vector is frequently used to identify equivalent set in the data (indistinguishable sets of errors).
Estimated size for a single error b is calculated by the Equation 12, which is based on signature vector, residual vector and variance-covariance matrix of the residual vector (Narasimhan & Mah, 1987):

Since independent estimated size of the identified gross errors could be incorrectly set, some authors (Jiang & Bagajewicz, 1999; Narasimhan & Jordache, 2000) have suggested calculating the size of identified gross errors simultaneously. For this case, let L be equal to the set of ej vectors (identified gross errors), i.e. L=[e1, e2...ez], then, fk is calculated as follows:

The subsequent vectors ej (e2, e3...en) represent gross errors detected by MT when the first estimations of b have been previously computed and added to respective suspicious measurements. This modification of fk allows calculating the vector b with the Equation 12.
Detectability and Identifiability
Even when GED techniques usually provide accurate results about failures and locations of gross errors in data, this information is not always reliable. In its performance, GED techniques cannot always distinguish where a gross error is located. Also, GED methods sometimes cannot detect gross errors in some special variables. In order to explain these issues, the concepts of detectability and identifiability are explained.
Detectability is a factor used for determining the probability of finding a gross error in a measurement. This factor depends on the contribution of a measurement on the model constraints (balances) and the standard deviation of such measurement. Hence, if a variable has a low standard deviation, a gross error in this variable cannot be easily detected (Madron, 1992; Narasimhan & Jordache, 2000). The detectability concept was considered in this work so as to detect possible fails in the GED methods.
On the other hand, identifiability concept is related to the capacity for distinguishing a gross error in a measurement from a gross error in any other measurement (Narasimhan & Jordache, 2000). Statistics tests of different variables are identical when the columns of balance matrix are linearly dependent, due to low redundancy degree. These variables are known as parallel streams (Iordache, Mah & Tamhane, 1985) and hinder the gross errors location. Since this problem is crucial in the DR and GED results, the identifiability concept was regarded during the development of the tool proposed in this paper. Difficulties in gross error distinguishing can be explained by the equivalency theory, developed by Bagajewicz and Jiang (1998).
Measurement Error Covariance Matrix Estimation
To calculate the reconciled vector (Y) (Equation 2) is necessary to estimate the measurement error covariance matrix (SR). SR is a symmetric matrix, formed by individual variance of each meter on the matrix diagonal. Off diagonal elements represent covariance between measurements. These correlations are generally neglected (Bagajewicz, 2010; Narasimhan & Jordache, 2000).
Variance estimation can be performed by either direct or indirect methods (Narasimhan & Jordache, 2000). The direct method assumes a fundamental condition steady-state; thus it cannot be applied to natural gas distribution network because volumetric flows constantly change according to user consumption, therefore stationary state is not achieved. On the other hand, the indirect method, proposed by Almasy and Mah (1984), is based on residual vector and requires lacks of gross errors in the data. However, this condition cannot be guaranteed, hence it is not possible to use the indirect method on natural gas distribution systems either.
Due to issues related to variance estimation, the assumptions suggested by Serth and Heenan (1986) were implemented in this work. In their research, Serth and Heenan (1986) assumed standard deviation as a percentage of the corresponding measure and variance as the square of such value. This heuristic approximation is valid for simulation purpose. In this contribution the standard deviations were set one percent of the measurements.
3. METHODOLOGY
Algorithm
There are two problems in applying any DR and GED technique on natural gas distribution systems, low detectability and parallel streams. These problems make it difficult to locate gross errors. When maximum measurement tests are in parallel streams, gross errors cannot be identified, thus the reconciled value will be incorrectly adjusted. In these cases, Cauchy method is proposed as a solution, since this method account for gross errors effect in its equation (Özyurt & Pike, 2004). Therefore, accurate reconciled values can be obtained.
On the other hand, although accurate reconciled can be obtained, gross error location is not possible by traditional techniques. For these cases, the X84 method is proposed as a solution because, unlike MT and GT, it is based on robust statistics; hence, its results are not affected by outliers.
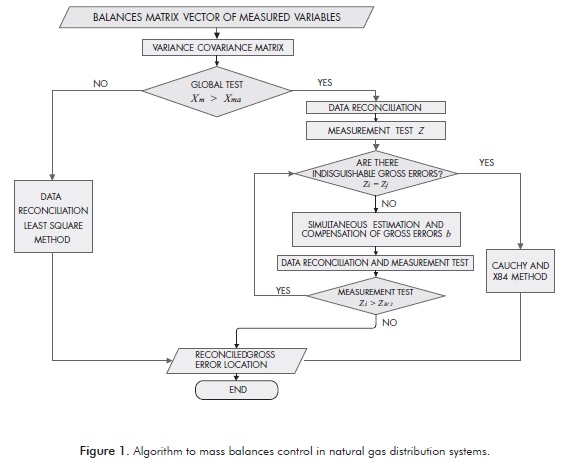
The algorithm is shown in Figure 1. This can be summarized as follows:
-
Enter the input data which correspond to system features.
-
Compute the measurement error covariance matrix (SR) as a percentage of the measures.
-
Compute GT in order to avoid searching of nonexistent gross errors in data by MT, hence calculation time decreases. If GT declares no gross errors, compute DR by least square method, print results and stop. Other-wise go to step 4.
-
Compute DR and MT to locate measurements which possibly contain gross error.
-
Assess if the greatest statistics test is identical for different variables. If it is, compute DR by Cauchy and GED by the X84 methods, results are printed and stop. Otherwise, go to step 6.
-
Estimate simultaneously gross error size vector b and add it to the detected measurements. Run the DR and compute MT. If gross errors are not detected, print results and stop, otherwise go to step 5.
This algorithm was developed in MATLAB through usage of Statistic toolbox and Optimization toolbox, on an Intel Core i5 PC, 2.90 GHz and 4 GB RAM.
4. RESULTS
Validation
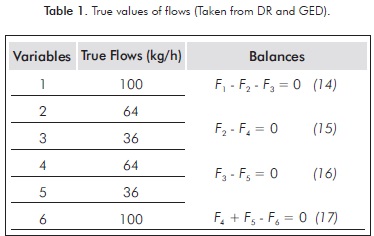
A heat exchanger process with separator and mixer units (Figure 2) was selected to validate the tool. This system was taken from DR and GED (Narasimhan & Jordache, 2000). True values of mass flow for each stream are shown in Table 1.
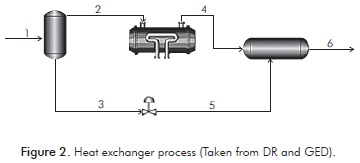
In order to validate the developed tool, randomly distributed errors (random and gross) must be introduced at real flows (Table 1). For this purpose, This method generates a series of random values Monte Carlo Method, from Microsoft Excel, was used.
This method generates a series of random values (errors) from a standard normal distribution, which were added to the real flow rates in order to simulate bias. Leakages are not simulated in this work. One thousand simulation trials of mass flow values were computed, according to the recommendations by Narasimhan and Jordache (2000). The numbers of gross errors were not restrictive, hence simulations ran from zero to six errors.
The path followed by this example in the algorithm is described by the set of step explained in the last section. Nonetheless, since this system does not have parallel streams, i.e. MT scores are not identical for any set of variables, reconciled estimations computed by Cauchy method will not be carried out.
Validation results were evaluated by comparing the difference between reconciled values and true values versus their expanded deviations, which were calculated by multiplications standard deviations by coverage factor, k. In this work, the coverage factor was set equal 2, thus the expanded deviations is twice standard deviations. Thus, if the difference between reconciled and the true values of a measurement is greater than their expanded deviations, reconciled value is considered not properly adjusted.
GED analyses were accomplished by calculating three performance measures. The two first measures were proposed by Narasimhan and Mah (1987) and the last one was proposed by Rollins and Davis (1992) (Sánchez, Romagnoli, Jiang & Bagajewicz, 1999). These parameters are given by Equations 18 to 20.



Validation Results
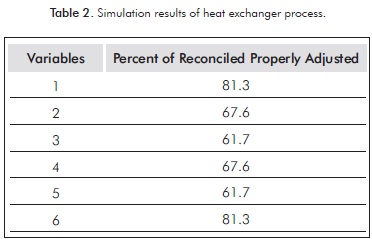
The results obtained by the developed algorithm are shown in Table 2. The percentages of the flows are calculated from 1000 simulation trials. It can be noticed from Table 3 that the algorithm obtained the correct results for DR, because the percentage of reconciled properly adjusted was greater than 60% for each variable (Serth & Heenan, 1986).
The results obtained by gross errors performance measures on the heat exchanger system are shown in the Table 3:
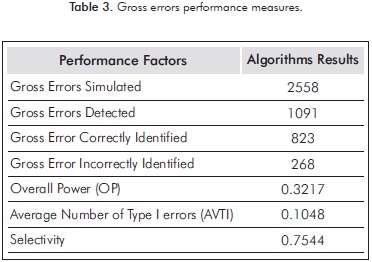
It can be observed from Table 3 that the identification, estimation and compensation of gross errors did not achieve satisfactory results since OP is small, even when AVTI is small and Selectivity is large. This weak performance of the tool can be explained by the follo-wing assertions:
-
Since standard deviations were estimated as one percent of measurements, variables, whose order of magnitude is small, like flows 3 and 5, had small standard deviations in comparison with remaining flows, whereby low detectability. This hinders gross errors detection in such variables.
-
In the heat exchange system, flows 2, 3, 4 and 5 form a cycle. Hence, according to theory of equivalency set of gross errors proposed by Bagajewicz and Jiang (1998), a set of three errors in any combination of these flows cannot be distinguished from any other combination. This problem could lead algorithm into inappropriate estimation and neglecting of some gross errors.
-
Since no restrictions were used in gross errors generation, in some cases, detection capacity of the system was overcome, i.e. sometimes there were more gross errors than restrictions (mass balances). This could lead algorithm into inappropriate gross error estimation.
-
In some cases, GT detected gross errors that MT could not locate. This phenomenon occurred because of the contribution of each measurement to residual vector, which lead it to fail the GT. Nonetheless, errors in those flows were individually small; therefore, MT did not detect them. It is important to mention that re-conciled values
Considering these issues, some cautions must be considered to guarantee a suitable functioning of the tool.
-
Detectability is a problem with no easy solution. Additional instrumentation and restriction equations could be helpful (Narasimhan & Jordache, 2000), but that is not always possible.
-
Regarding to equivalent sets of gross errors, a database of historical of equipment failures could be used in order to choose sets with larger failure frequencies (Bagajewicz, 2010). Nonetheless, these sets must be validated by inspecting flow meters.
-
To avoid that gross errors overcome detection capacity of the system, activities of metrological assurance must be carried out in order to decrease the likelihood of instrument failures.
Natural Gas Distribution Network Analysis
The analyzed natural gas distribution system (Figure 3) delivers gas to different towns located south of Colombia. Initially, natural gas is transported by Transporter number one (national transporter). It delivers the combustible to Transporter number two (regional transporter), which in turn transports the gas through a steel pipeline system until City Gates, where it is received by a natural gas distribution company. In these city gates, pressure is regulated in order to make natural gas suitable to deliver it to approximately 740000 residential, commercial and industrial consumers. The natural gas is distributed into three different towns, identified as FCGi. City Gates two and three did not report measurements, hence they do not appear in the figure. The FCGi represent residential and industry measurements. Additionally, some residents and industries measurements are conveyed in one measurement by the distribution company to facilitate the account production.
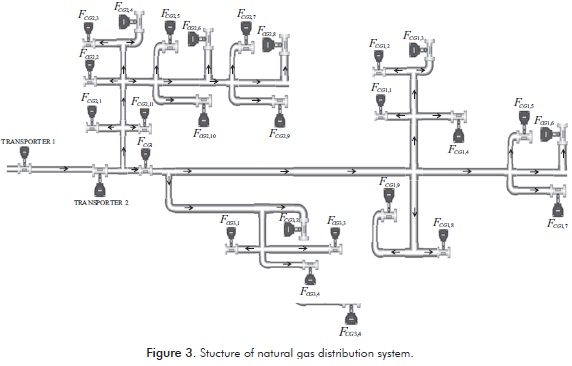
The material balances on this system are shown in the following equations:
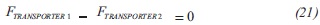
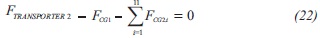
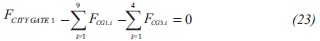
These summations regard every gas delivery, residential, commercial and industrial consumer.
According to Colombian laws (Registro Único de Transporte, RUT), standard deviation of the meter in a natural gas distribution system must be 1%, whereby in this work, standard deviations were 1% of the corresponding measures. Variance is square of this value.
Results of Natural Gas Distribution Network
In Table 4, volumetric measurements from natural gas distribution system and their MT (Zi) are shown. The MT criterion (Zβ/2) is 3.11, thus, if the greatest test (Z) from data is greater than such criterion, then the measurement is identified as the gross errors container.
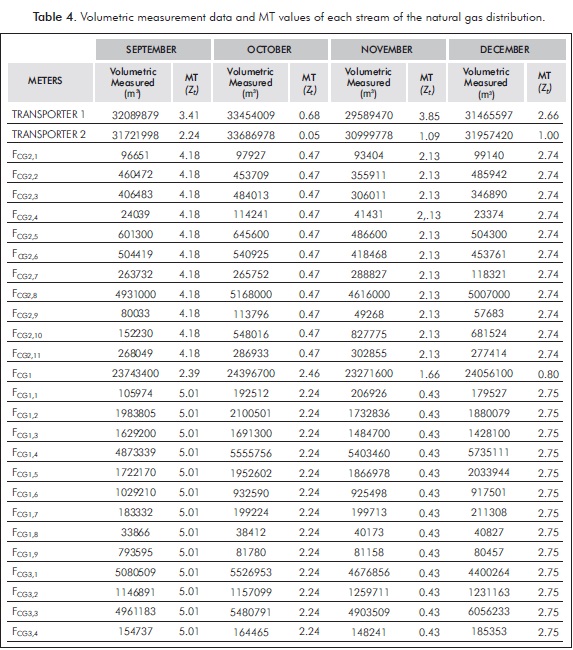
According to Table 4, on September, the maximum test was located in the parallel streams FCG1,i and FCG3,i, thus they are suspected to contain gross errors. It is important to mention that MT scores of some measurements could have been affected by the presence of gross errors (smearing effect). Since GED is impossible, the Cauchy and the X84 methods were used in this case. In October, gross errors were not identified because statistic tests did not overcome the test criterion. In November, a gross error was identified in the meter of the Transporter 1, which size was estimated in -1195595 m3. In December, GT detected gross errors that MT did not locate. For this case, the X84 method was applied in order to try locating gross errors.
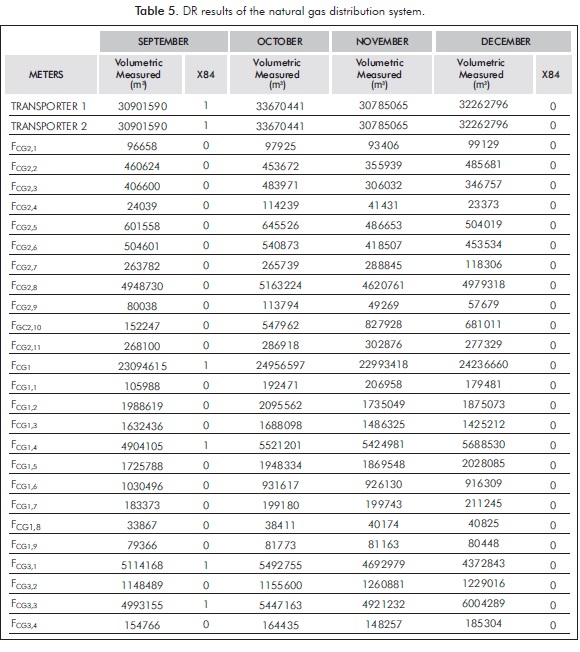
In Figure 4, residuals from the mass balances of 4 months are shown. Notice that none is equal to zero. It can also be noticed that even when all MT scores of the first month are larger in comparison with other ones, results seem to be better. This could be explained by compensations of errors. Furthermore, it is important to mention that differences presented in Figure 4 could be equivalent to more than 560 million COP (international currency code of Colombia) in revenue losses for either transporter or natural gas distributors.
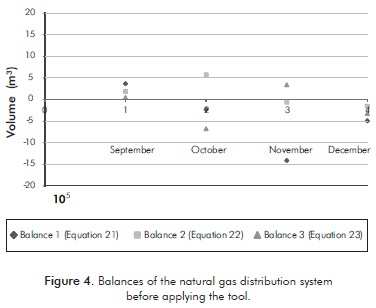
Table 5 shows the results obtained by the proposed tool. From this table, it can be noticed that the X84 method located gross errors in six streams in September, parallel streams FCG1,4, FCG3,1 and FCG3,3, City Gate 1 and Transporter 1 and 2. This method denotes suspicious measurements by one and zero elsewhere, using a k value equals 3. The X84 technique declared measurements with larger standard deviations as suspicious of containing gross errors, neglecting the presence of gross errors in measurements with smaller ones, thus, correct detection of gross errors cannot be guaranteed. For this reason, as it was already mentioned, a database of historical of equipment failures and flow meters inspections must be used to choose sets of gross error container. Furthermore, most of the measured flows in the parallel streams are made periodically; hence GED on natural gas distribution systems could be delayed. Finally, there are several meters on natural gas distribution system, therefore error probability increases considerably.
In December, gross errors were not detected by the X84 method or MT even when GT detected them, because measurements were poorly adjusted. This case also occurred in the validation example. In such case, the reconciled were correctly set; consequently, the December-results can be assumed as accurate.
In Figure 5, the results of the balance after applying the tool are shown. It can be noticed how imbalances have been significantly reduced.
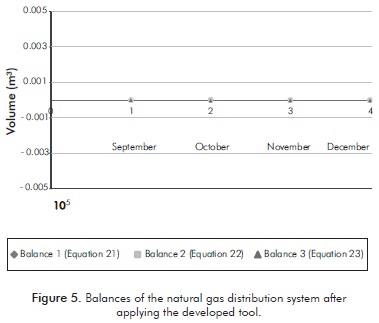
From the results, it can be noticed that in two out of the four analyzed months, gross errors were detected on the measurements of Transporter 1. This demonstrates a high probability of failure of its meter, which agrees with report received from the Natural Gas Distribution Company.
5. CONCLUSIONS
-
A tool, based on DR and GED techniques, was developed. This tool attempts to identify instrument failures (gross errors), which can generate imbalances and invoicing problems to the natural gas distribution company.
-
The tool was validated by a typical literature problem. The results were satisfactory to DR. Furthermore, execution time was short for the computer used. Nonetheless, some issues related to GED techniques, such as low detectability and equivalent sets of gross errors, were found. To solve these problems, appropriate solutions were proposed, for instance a data base to measure historical equipment failure and activities of metrological assurance.
-
An analysis about the natural gas distribution network was carried out. In this analysis, some restrictions were identified to apply DR and GED techniques on such system, small detectability and parallel streams. For those problems, nonconventional techniques of DR and GED were proposed. These techniques avoid using additional meters, which require great economic investment, modular software and non-linear boundaries, which increase computation time. Considering DR, Cauchy function was proposed for cases of errors on parallel streams, in order to obtain appropriate reconciled results, even in the presence of gross errors. The X84 method was proposed as an alternative GED technique. This method attempts to identify gross errors on parallel streams. Nevertheless, these detections are not reliable since gross errors in measurements with low standard deviations are neglected. Accurate estimation of standard deviations could be achieved through metrological analysis of measuring equipment, in order to make the results reliable.
-
Finally, it was shown that the obtained results were in agreement with reports received from the distribution company.
ACKNOWLEDGEMENTS
The authors would like to thank Corporación Centro de Desarrollo Tecnológico de GAS for supporting the development of this work.
REFERENCES
Almasy, G. & Mah, R. S. H. (1984). Estimation of measurement error variances from process data. Ind. Eng. Chem. Process Des. Dev., 23(4), 779-784. [ Links ]
Bagajewicz, M. J. & Jiang, Q. (1998). Gross error modeling and detection in plant linear dynamic reconciliation. Comp. Chem. Eng., 22(12), 1789-1809. [ Links ]
Bagajewicz, M. J. & Cabrera, E. (2003). Data reconciliation in gas pipeline systems. Ind. Eng. Chem. Res., 42(22), 5596-5606. [ Links ]
Bagajewicz, M. J. (2010). Smart process plants. Software and hardware solutions for accurate data and profitable operations. New York: McGraw-Hill. [ Links ]
Crowe, C. M. (1996). Data reconciliation-progress and challenges. J. Process Control, 6(2-3), 89-98. [ Links ]
Fusiello, A., Trucco, E., Tommasini, T. & Roberto, V. (1999). Improving feature tracking with robust statistics. Pattern Analysis & Applications, 2(4), 312-320. [ Links ]
Heenan, W. A., Cardiel, M. G. & Serth, R. W. (1987). Gross error detection and data reconciliation in natural gas distribution systems: A feasibility study. American Institute of Chemical Engineers spring national meeting, Houston, TX, USA. Technical Paper 67b. [ Links ]
Iordache, C., Mah, R. S. H. & Tamhane, A. C. (1985). Performance studies of the measurement test for detecting gross errors in process data. AIChE J., 31(7), 1187-1201. [ Links ]
Jiang, Q. & Bagajewicz, M. J. (1999). On a strategy of serial identification with collective compensation for multiple gross error estimation in linear data reconciliation. Ind. Eng. Chem. Res., 38(5), 2119-2128. [ Links ]
Kuehn, D. R. & Davidson, H. (1961). Computer control. II. Mathematics of control. Chem. Eng. Progress, 57(6), 44-47. [ Links ]
Madron, F. (1992). Process plant performance: Measure ment and data processing for optimization and retrofits. Chichester: Ellis Horwood Limited. [ Links ]
Mah, R. S. H., Stanley, G. M. & Downing, D. M. (1976). Reconciliation and rectification of process flow and inventory data. Ind. Eng. Chem. Process Des. Dev., 15(1), 175-183. [ Links ]
Mei, C., Su, H. & Chu, J. (2006). An NT-MT combined method for gross error detection and data reconciliation. Chinese J. Chem. Eng., 14(5), 592-596. [ Links ]
Narasimhan, S. & Mah, R. (1987). Generalized likelihood ratio method for gross error identification. AIChE J., 33(9), 1514-1521. [ Links ]
Narasimhan, S. & Jordache, C. (2000). Data reconciliation & gross error detection. An intelligent use of process data. Houston: Gulf Publishing. [ Links ]
Oliveira, E. C. & Aguiar, P. F. (2009). Data reconciliation in the natural gas industry: Analytical applications. Energy & Fuels, 23(7), 3658-3664. [ Links ]
Özyurt, D. B. & Pike, R. W. (2004). Theory and practice of simultaneous data reconciliation and gross error detection for chemical processes. Comp. Chem. Eng., 28(3), 381-402. [ Links ]
Rollins, D. K. & Davis, J. F. (1992). Unbiased estimation of gross errors in process measurements. AIChE J., 38(4), 563-572. [ Links ]
Sánchez, M., Romagnoli, J., Jiang, Q. & Bagajewicz, M. (1999). Simultaneous estimation of biases and leaks in process plants. Comp. Chem. Eng., 23(7),841-857. [ Links ]
Serth, R. W. & Heenan, W. A. (1986). Gross error detection and data reconciliation in steam-metering systems. AIChE J., 32(5), 737-742. [ Links ]