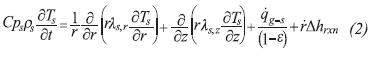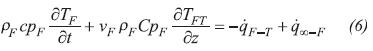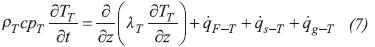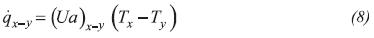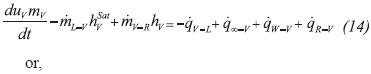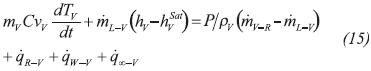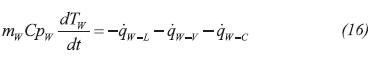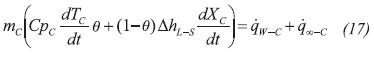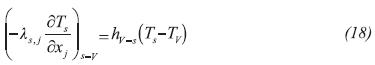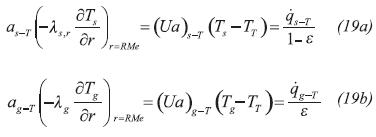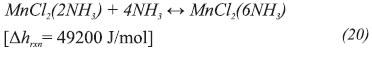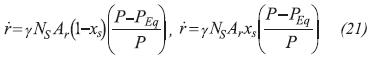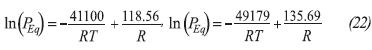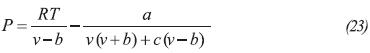Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
CT&F - Ciencia, Tecnología y Futuro
versão impressa ISSN 0122-5383
C.T.F Cienc. Tecnol. Futuro vol.5 no.3 Bucaramanga jul./dez. 2013
UNSTEADY NUMERICAL SIMULATION OF DYNAMIC REACTOR - EVAPORATOR INTERACTION IN THERMOCHEMICAL REFRIGERATION SYSTEMS
SIMULACIÓN NUMÉRICA DE LA INTERACCIÓN REACTOR - EVAPORADOR EN SISTEMAS DE REFRIGERACIÓN TERMOQUÍMICOS
Juan M. Mejía1*, Farid Chejne1 and Farid B. Cortés1
1Department of Energy and Processes - Faculty of Mines, Universidad Nacional de Colombia, Medellín, Antioquia, Colombia
E-mail: jmmejiaca@unal.edu.co
(Received: Jul. 02, 2013; Accepted: Nov. 18, 2013)
*To whom correspondence should be addressed
ABSTRACT
Close interaction between evaporation/reaction rates in gas-solid refrigeration cycles promotes the dynamic behavior of gas pressure in gas-liquid and gas-solid interfaces in evaporators and reactor diffusers. Simultaneously, gas pressure modifies both reaction rates in reactors and mass and energy transfer rates in reactors and evaporators. The objective of this work is to model the complex interaction between reactor and evaporator using a phenomenological approach. The coupled interaction is studied by a novel mathematical model of the reactor and evaporator at the synthesis/evaporation step. The model of the gas-solid reactor is based on unsteady 2-D mass, momentum and energy transport equations. The evaporator model considers the interaction between evaporation/reaction rates given by the unsteady mass and energy transfer at heterogeneous interfaces and with other components. The thermodynamic properties of the refrigerant are calculated by the Patel-Teja equation-of-state. Simulation results predicted by the model were satisfactorily validated with experimental data. Predicted interaction between reactor, evaporator and cooling space showed non-linear behavior of gas pressure. The simulation results showed that, if the dynamics of the evaporator and cooling space are neglected, coefficient of performance (COP) is overestimated by 32% for the configuration evaluated in this work.
Keywords: Simulation, Mathematical modeling, Refrigeration, Evaporator, Reactor, Dynamic state.
RESUMEN
Existe una interacción entre las tasas de reacción/evaporación en ciclos de refrigeración gas-sólido, promoviendo un comportamiento dinámico de la presión en las interfaces gas-líquido y gas-sólido en el evaporador y reactor. Simultáneamente, la presión modifica tanto la velocidad de reacción en el reactor como las tasas de transferencia de materia/energía en el evaporador y reactor. El objetivo de éste trabajo es modelar la interacción evaporador-reactor basado en una aproximación fenomenológica. Ésta interacción es estudiada mediante un nuevo modelo matemático del reactor y evaporador durante la etapa de síntesis/evaporación. El modelo del reactor gas-sólido está basado en ecuaciones 2-D de transporte de materia, momentum y energía. El modelo del evaporador considera la interacción dinámica entre las tasas de evaporación/reacción dadas por la transferencia de materia en las interfaces heterogéneas y de energía con otros componentes. El comportamiento termodinámico del refrigerante es estimado mediante la ecuación de Patel-Teja. Los resultados de la simulación son validados satisfactoriamente con datos experimentales. Las simulaciones mostraron un comportamiento no-lineal de la presión como consecuencia de la interacción entre el reactor-evaporador-refrigerador. Los resultados sugieren que, si las dinámicas del evaporador-refrigerador son despreciadas, el coeficiente de rendimiento (COP, por sus siglas en inglés) es sobreestimado en 32% para el sistema evaluado en éste trabajo.
Palabras clave: Simulación, Modelamiento matemático, Refrigerador, Reactor, Estado no-estacionario.
RESUMO
Existe uma interação entre as taxas de reação/evaporação em ciclos de refrigeração gás-sólido, promovendo um comportamento dinâmico da pressão nas interfaces gás-líquido e gás-sólido no evaporador e reator. Simultaneamente, a pressão modifica tanto a velocidade de reação no reator como as taxas de transferência de matéria/energia no evaporador e reator. O objetivo deste trabalho é moldar a interação evaporador-reator baseado em uma aproximação fenomenológica. Esta interação é estudada mediante um novo modelo matemático do reator e evaporador durante a etapa de síntese/evaporação. O modelo do reator gás-sólido está baseado em equações 2-D de transporte de matéria, momentum e energia. O modelo do evaporador considera a interação dinâmica entre as taxas de evaporação/reação dadas pela transferência de matéria nas interfaces heterogêneas e de energia com outros componentes. O comportamento termodinâmico do refrigerante é estimado mediante a equação de Patel-Teja. Os resultados da simulação são validados satisfatoriamente com dados experimentais. As simulações mostraram um comportamento não-linear da pressão como consequência da interação entre o reator-evaporador-refrigerador. Os resultados sugerem que, se as dinâmicas do evaporador-refrigerador são desprezadas, o coeficiente de rendimento (COP, por sua sigla em inglês) é superestimado em 32% para o sistema avaliado neste trabalho.
Palavras-chave: Simulação, Modelamento matemático, Refrigerador, Reator, Estado não-estacionário.
1. INTRODUCTION
In some rural areas not interconnected to the electric grid, refrigeration is a key aspect for suitable levels of comfort, vaccines and food conservation, and to achieve sustainable development. In these regions, refrigeration by sorption processes (absorption and adsorption) is a technological option for cooling: an important feature of sorption–based cycles is that they are powered by thermal energy, instead of electricity, using domestic or industrial waste heat, biomass, fossil fuels and solar energy. In addition, sorption processes use clean refrigerants, have low operational and maintenance cost, are silent and have a long lifetime (Ziegler, 1999).
The thermodynamic cycle of a gas-solid refrigeration system is constituted by one or more gas-solid chemical reactors evaporators and condensers. In a gas-solid absorption or thermochemical reactor a reversible, monovariant chemical reaction takes place between the gas (refrigerant) and a salt 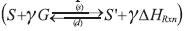 , where the synthesis reaction (s) is exothermic, and decomposition one (d) is endothermic (Stitou & Crozat, 1997). In the synthesis - evaporation step, the energy transferred to the evaporator evaporates the liquid phase and the gas reacts with the salt in the reactor. Synthesis reaction proceeds when the temperature of the reactive solid/gas in the reactor is lower than that in the equilibrium-constraining state at evaporator pressure (Le Pierrs, Stitou & Mazet, 2008). In the decomposition-condensation step, energy is transferred to the reactor to release the gas in the decomposition reaction and further condensate it in the condenser. The chemical reaction proceeds as temperature of the reactive solid/gas in the reactor at condenser pressure is higher than the equilibrium-constraining temperature/pressure (Le Pierrés et al., 2008). A complete description of the thermodynamic cycle can be found in Stitou and Crozat (1997).
, where the synthesis reaction (s) is exothermic, and decomposition one (d) is endothermic (Stitou & Crozat, 1997). In the synthesis - evaporation step, the energy transferred to the evaporator evaporates the liquid phase and the gas reacts with the salt in the reactor. Synthesis reaction proceeds when the temperature of the reactive solid/gas in the reactor is lower than that in the equilibrium-constraining state at evaporator pressure (Le Pierrs, Stitou & Mazet, 2008). In the decomposition-condensation step, energy is transferred to the reactor to release the gas in the decomposition reaction and further condensate it in the condenser. The chemical reaction proceeds as temperature of the reactive solid/gas in the reactor at condenser pressure is higher than the equilibrium-constraining temperature/pressure (Le Pierrés et al., 2008). A complete description of the thermodynamic cycle can be found in Stitou and Crozat (1997).
The system involves many unsteady, non-linear phenomena and the management of the cyclic working mode is an important scientific issue (Castets & Mazet, 2000). The development of mathematical models based on a phenomenological approach is essential for designing, optimizing and evaluating the system configuration and operating conditions.
Different modeling approaches for the reactor have been presented in literature, classified according to complexity in: local, global, analytical (Stitou & Crozat, 1997) and empirical models. Local models are based on unsteady mass, energy and momentum balance equations, so they provide more information on the system than other approaches. In the synthesis step, system pressure is lower than the decomposition step and solid permeability may decrease when the reaction proceeds. Mass transfer and transport phenomena become important (Lu & Mazet, 1999; Mazet & Lu, 1998) and must be taken into account in the formulation of the mathematical model.
A first approach in the modeling of mass transfer limitations in the synthesis step was proposed by Lu and Mazet (1999) by coupling unsteady mass and energy transport equations with chemical reactions at the grain level. Their results revealed the influence of operating pressure and permeability on process performance. This model has been used to study the performance of thermochemical reactors by changing both their operational and geometrical condition (Mazet & Lu, 1998; Jolly & Mazet, 1999; Dutour, Mazet, Joly & Platel, 2005). However, the model of Lu et al. (1996) assumes ideal gas behavior and local isothermal conditions of the solid and gas phases. It has also been observed in adsorption systems that uniform pressure assumption increases deviation from experimental observations up to 40% (Cortés, Chejne, Mejía & Londoño, 2009).
Previous models have neglected the dynamics of the evaporator and its interaction with the reactor, assuming constant evaporator pressure as one type of inlet boundary condition. Close evaporator-reactor interaction exists as the evaporation takes place: if more power is transferred to the evaporator, gas pressure and saturation temperature will increase and the reaction rate will change. These differences between evaporation and reaction rates change gas pressure and density at both the liquid/gas interface in the evaporator and at the gas/solid interface in the gas diffusers in the reactor. Therefore mass and energy transfer rates are not constant. Experimental observations by Lahmidi, Mauran and Goetz (2006), Mauran, Lahmidi and Goetz (2008) for SrBr2 + H2O working pair, and Li et al., (2011) for BaCl2 + NH3 and multisalt MnCl2 - SrCl2 + NH3, confirm that gas pressure during the evaporation step is not constant, i.e. it follows a dynamic behavior. Zhao, Hu and Blazewicz (2012) reported that the unsteady behavior of the evaporator and condenser provides transient boundary conditions to the gas - solid reactor model, improving the predictions of the mathematical model and reflecting the close interplay existing between mass and energy driving forces.
Few works account for the dynamic interaction between reactor and evaporator. A CaCl2/silica gel-water system was studied by Saha, Chakraborty, Koyama and Aristov (2009), who proposed a model for the evaporator based on global mass and energy balances for the liquid phase. However, it is assumed that the evaporation and condensation rates are given by the sorption and desorption rates, respectively. A similar approach was taken by Le Pierres, Mazet and Stitou (2007); Gong, Wang, Xia and Chen (2011); Wang et al. (2005); Wu, Zhang and Sun (2009). This approach neglects the mass transfer limitations in evaporation processes and the dynamics of the gas phase as well. At a given time step, for a constant volume in the evaporator, connecting pipes and gas diffusers in the reactor, gas pressure depends on evaporation/condensation and reaction rates, remaining mass of gas and its temperature. Therefore mass and energy balance equations for the gas phase are also important in the model formulation.
In this work, we propose and solve a two-dimensional, time-dependent model of a gas-solid absorption refrigeration system, where the dynamic behavior of gas pressure is accounted for by a mathematical model of the reactor and evaporator during the evaporation step. Main contributions of this work are: 1. the reactor model considers the non-local thermal equilibrium between the gas and solid phases; 2. thermodynamic properties of the gas phase are calculated by a cubic equation of state; 3. a new thermodynamic-consistent model for the evaporator is proposed and coupled to the reactor model, which considers the dynamics of liquid and gas phases. The mass of the gas phase evolves according to the difference between the gas produced from the liquid phase and the gas reacting at the reactor; 4. the transient behavior of the reactor is instructively presented in the form of the instantaneous contour plots, where the controlling mechanisms of the chemical reaction can be easily identified.
2. MATHEMATICAL MODEL
System performance can be analyzed by solving mass, energy and momentum balance equations (Bird, Stewart & Lighfoot, 2002; Velásquez & Chejne, 2004) for each subsystem, using appropriate boundary conditions. These equations and their simplifying assumptions are presented in this section for the reactor, evaporator and cooling space.
Reactor
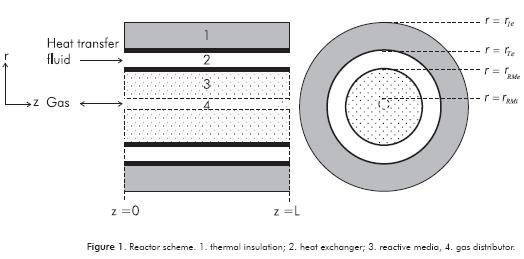
Heat recovery or heat wave geometric configuration has been chosen for the reactor (see Figure 1). The reactor is made up of a cylinder filled with a salt or a Reactive Medium (RM). A gas distributor is placed at the center of the reactor, and there is a heat exchanger at the external annulus that is thermally-isolated from surroundings. Based on reactor geometry, we chose the cylindrical coordinate system for writing the transport equations.
Solid Phase
As the heterogeneous chemical reaction takes place at the solid phase (S + γ G ↔ S' + γΔHrxn ), the concentration of the product increases as reaction proceeds according to the following equation:
Equation 1a can be expressed using the reaction conversion, as follows
The energy transport equation of the solid phase considers the conduction transport mechanism in the axial and radial directions. Because the gas entering the reactor and the solid phase can have different temperatures, there is an energy transfer between these phases. In addition, heat can be released or consumed by the thermochemical reactions taking place between the gas and solid phases. Previous mechanisms are expressed in the following energy equation for the solid phase:
In Equation 2, the term on the Left Hand Side (LHS) accounts for the accumulation of energy in a differential volume element, the first and second terms on the Right Hand Side (RHS) denote heat conduction in radial and axial directions, the third term on the RHS represents the energy transfer with the gas phase, and the last term on the RHS is a source/sink of energy required by thermochemical reactions in order to proceed.
Gas Phase
The transport of the gas phase through the porous matrix is driven by pressure gradients and can be described by Darcy’s law. The permeability of the porous matrix depends on characteristic parameters of the medium, e.g. porosity, average pore diameter and tortuosity. Neglecting buoyant forces, the momentum equation for the gas phase follows Darcy’s law:
Following a similar procedure to that of the energy equation of the solid phase, the mass transport equation considers that the gas is transported through the porous media by convection and reacts with the solid phase. The equation reads:
Convection and diffusion (conduction) mechanisms are responsible for energy transport in the gas phase. The energy transport equation must take into consideration the energy transfer with the solid phase:
Note that internal energy in Equation 5 is used for the accumulation term instead of a simplified expression leading to enthalpy, i.e. neglecting the work flow by expansion and compression. This term provides a more general situation where stiff changes in both gas pressure and pore volume occur within the reactor. The internal energy is calculated using an equation of state described below.
One important aspect in the reactor configuration is the heat wave or heat recovery working mode using an energy-transporting fluid (Heat Transfer Fluid –HTF–). This fluid transfers energy to the reactor in the condensation/decomposition step and vise-versa in the evaporation/synthesis step. The HTF flows through the heat exchanger by forced circulation so radial temperature gradients are omitted. In addition, the conductive transport mechanism in heat transfer is less important than the convective. Because the fluid wets the reactor wall and the outer shell, the corresponding transfer terms are represented in the RHS of the HTF energy equation (Equation 6)
The dynamics of the reactor wall must also be included in the reactor model because energy can be accumulated in the material and transported in the axial direction as reactions proceed. The energy transfer between the wall and the HTF, solid and gas phase of the reactor are included respectively in the last three terms on the RHS of the wall energy transport equation (Equation 7)
External heat transfer flows (qxy) in Equations 2, 5 and 7 denote the heat transfer between subsystems x and y:
Where U is the overall heat transfer coefficient and a is the heat transfer area per unit of volume.
Evaporator
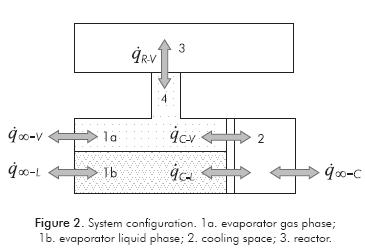
A scheme of the evaporator model is presented in Figure 2. The evaporator model considers two homogenous phases (liquid and gas). The liquid mass that remains in the evaporator at a given time depends on the evaporation rate:
Where the evaporation rate (mL-v) is expressed as follows:
The energy balance equation for the liquid phase considers the heat transfer with: the evaporator walls (qw-L), gas phase (qv-L) and the advected flow of energy associated with the flow of gas leaving the liquid phase (mL-v hysat):
Assuming that the liquid is incompressible, CvL≈CpL the RHS of Equation 11a is conveniently expanded as follows:
Introducing Equation 11b into Equation 11a, and recognizing that u=h-P/ρ, the energy balance equation of the liquid phase reads:
For a given geometrical configuration, heat transfer areas between evaporator and cooling space can be obtained as a function of the liquid level by solution of Equation 9.
The control volume of the gas phase is taken as the evaporator gas space, the pipes that connect the evaporator with the reactor and the distributors in the reactor. The mass balance equation for the gas phase is given by the difference between evaporated mass flow rate and the rate of gas crossing the reactive media boundaries due to chemical reactions (mv-R):
Like the energy equation of the liquid phase, the energy equation of the gas phase considers the advected flows of energy from the liquid phase and that transferred to reactor and the heat transfer with the liquid phase, surroundings, evaporator wall and the solid phase at the gas distributor of the reactor. The equation reads:
The evaporator wall transfers energy with liquid and gas phases with the water in the cooling space:
Condenser
The dynamics of the condensation/decomposition step is also controlled by the interaction between the reactor and evaporator. Equations 9-16 can be modified in order to propose a model for the condenser, changing qw-c by qw-∞ in Equation 14 and modifying the heat transfer terms accounting for the expected flow patterns. Because the decomposition reaction is controlled by the heat transfer mechanisms and the condenser area (a design parameter) is large enough to condense the released gas, condenser pressure is nearly constant during the step. We run several calculations including a vertical condenser model and the simulation results showed a constant pressure behavior at the condenser. Therefore we assume that the pressure at the condenser is constant.
Cooling Space
Direct water freezer arrangement contact is established for the cooling space. A global model that consider latent and sensible heats is formulated; it is assumed that water properties change linearly with the solidification conversion (Xc) when the phase change occurs. A flag (θ) is used to switch the accumulation term between latent and sensible heats: θ =0, for TC = 273.15 K and 0 < Xc < 1; θ = 1, for TC ≠ 273.15 K . Heat transfer with the evaporator wall and surroundings is considered in the equation:
This simple model can also be used in modeling heat influx in conventional and advanced refrigeration cycles, such as the magnetic cycle (Hoyos et al., 2006).
Boundary Conditions
The coupling between the reactor and evaporator/condenser is accomplished at the inlet/outlet boundaries of the reactive media (0 ≤ z ≤ L, r = rRMi ; rRMi ≤ r ≤ rRMe, Z =0; rRMi ≤ r ≤ rRMe, Z =L) where a pressure boundary condition is imposed on gas density, momentum and energy equations. The pressure on the outer surface of the reactive media is imposed by the evaporator or condenser. At these phases, a Newmann-type boundary condition is chosen for the solid energy balance equation:
Non-flow condition 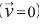 is set up for gas flow in the reactor external wall (0 ≤ z ≤ L, r = rRMe) and Newmann boundary condition for gas and solid energy equations:
is set up for gas flow in the reactor external wall (0 ≤ z ≤ L, r = rRMe) and Newmann boundary condition for gas and solid energy equations:
At the reactor wall boundaries (z=0 and z=L), an adiabatic conditions is assumed for the wall energy equation, and a Dirichlet boundary condition for the HTF because inlet temperature is known a-priori.
Numerical Solution
Partial differential equations describing the dynamic behavior of the reactor were discretized using the finite volume method (Verteeg & Malalasekera, 1995). A second order scheme was implemented for discretizing spatial terms in partial differential equations. This process provides a set of Ordinary Differential Equations (ODE) that are coupled to evaporator equations. This set of ODEs and the constitutive relations provide a closed mathematical system. Because of the non-linear, stiff behavior of the resulting ODE system, gear method was used for time integration by setting up a tolerance of 10-6. The in-house code was programmed in Fortran. Mesh size was optimized by a successive mesh refinement procedure until non-significant changes were observed in both exit HTF temperature and global reaction conversion. The resulting mesh size has 10×50 finite volumes in radial and axial directions, respectively.
Test Case
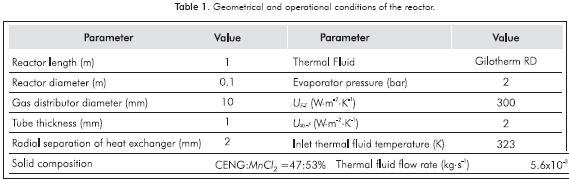
In order to evaluate the model proposed in this work, experimental results from Goetz and Llobet (2000) are compared to simulation results. The reactor is constituted by a cylinder filled with chlorine salt. A gas distributor is placed at the center and in the external annulus, there is a heat exchanger that is thermally-isolated from the environment. The reactor has the same design as that tested by Pons, Laurent and Meunier (1996). Geometric configuration and operating conditions for the synthesis step are listed in Table 1. The solid phase is made of MnCl2 impregnated on Compressed Expanded Natural Graphite (CENG), which reacts with ammonia. Although this material has the following properties: anisotropic behavior (Olives & Mauran, 2001), high porosity, particles with non-spherical shape, consolidated porous medium and multi-mode or very large grain or pore size distribution, Mauran, Rigaud and Coudevylle (2001) showed that the Carman-Kozeny correlation (Kasta, & Hohenthanner, 2000) can be successfully applied to CENG, so Darcy’s law is still valid for describing the gas transport trough the reactive media.
The chemical reaction that takes place in the reactor is:
The following reaction rates are used (Dutour et al., 2005) for the synthesis and decomposition reactions, respectively:
Where γ=4, NS = 1068 mol.m-3, Ar= 3.3×10-3s-1 (Dutour et al., 2005). The equilibrium pressure for the synthesis and decomposition reactions are presented in Equation 22 (Goetz & Llobet, 2000).
Properties and constitutive relations for the reactive medium are presented in Table 2.
Thermodynamic properties of the gas phase are calculated by the Patel and Teja (1982) equation of state:
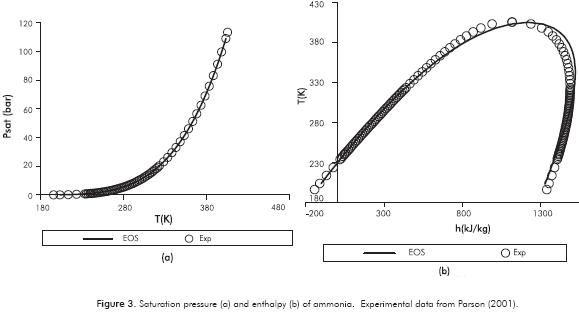
The comparison between experimental data of saturation pressure and enthalpy for different temperatures reported by the ASHRAE Handbook (Parson, 2001) and the theoretical data from the solution of the Patel-Teja equation (1982) are presented in Figures 3a and 3b, respectively.
On the other hand, thermal conductivity and viscosity of ammonia were correlated using experimental data (Parson, 2001).
3. RESULTS AND DISCUSSION
Test Case Results
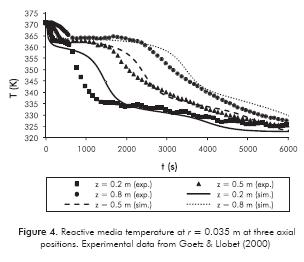
Given the operating conditions in Table 1, the temperature of the reactive media is presented in Figure 4.
The chemical reaction starts when RM temperature is below equilibrium one (TEq = 365 K for P = 2 bar) and heat is released because of the exothermicity of the synthesis reaction. Reaction heat is transferred to the thermal fluid to keep the reaction away from the equilibrium state. This is why at the onset of the reaction there is a “flat” temperature profile for the axial positions shown in Figure 4: the closer the point is to the HTF inlet, the lower the RM temperature will be. The reaction rate becomes high and the length (or duration) of this zone will be short; so heat transfer is the controlling mechanism. The Root Mean Square error (RMS) between the numerical simulations and experimental data is 3.36, 1.35 and 2.54 K for the Z = 0.2, Z = 0.5 and 0.8 m curves in Figure 4.
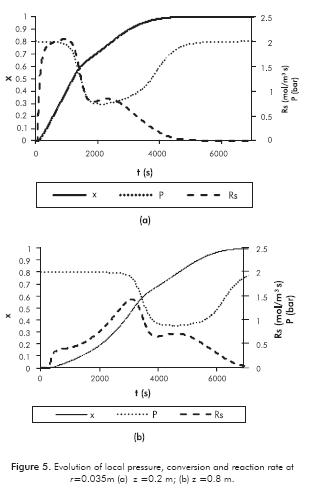
When local conversion is greater than 0.3, RM permeability decreases and it is expected that mass transfer limitations become important (see Figures 5a and 5b). An important drop in pressure and reaction rate occurs. Consequently, temperature will also drop faster in this region as shown in Figure 4. It is also noted in Figures 5a and 5b that there is a second local maximum in reaction rate when conversion is around 0.8. After this point, pressure increases to the initial value. Although the pressure is high enough to have a significant difference regarding the equilibrium value (Equations 5 and 7), it does not have a significant impact on reaction rate. Chemical kinetics play an important role.
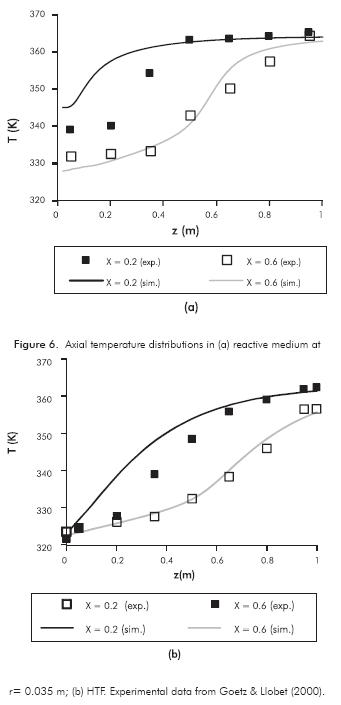
Instantaneous axial temperature profiles of the RM and HTF are shown in Figures 6a and 6b respectively for X = 0.2 and X = 0.6. In these plots, the HTF inlet is located at z = 0.
In Figure 6a, it is observed that, although there is an overestimation of the temperature for z < 0.5 m and X = 0.2, the model exhibits the experimental shape of the temperature, i.e. the temperature wave. Particularly, when the global conversion is 0.6 (Figure 6b), the simulation results are very close to experimental values. The maximum RMS deviation between simulation results and experimental data is 2.88 K (RM temperature X = 0.2 in Figure 6a).
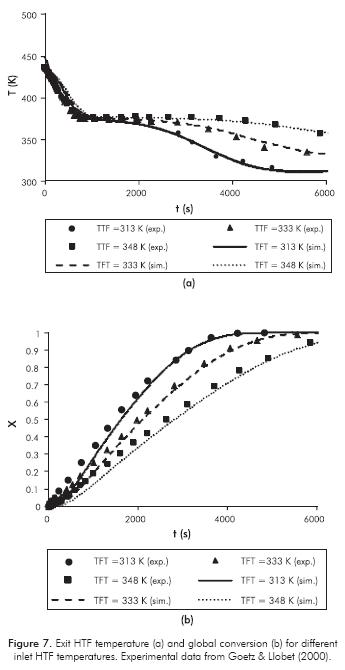
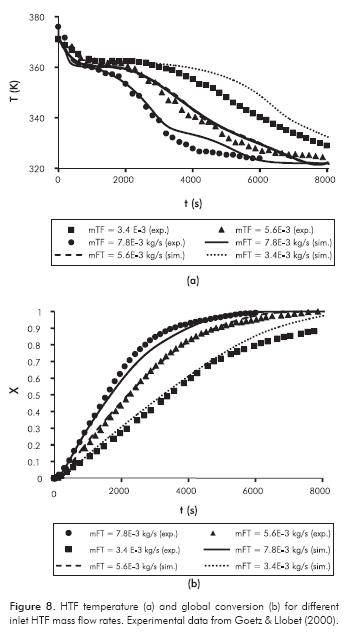
The model sensitivity in the heat transfer between RM and HTF is presented in Figure 7 for different inlet HTF temperatures (Pevap =3.5 bar, mF =5.6×10-3 kg.s-1) and in Figure 8 for different mass flow rates (Pevap=2 bar, TF,i =313 K). In the latter case, the heat transfer coefficients between HTF and reactor, estimated by Goetz and Llobet (2000), were used in the simulations.
If more power is transferred to the HTF, the stage duration will be shorter as can be observed in Figures 7 and 8. It is noted in both Figures that, although the simulation results fit experimental data very well for = 5.6×10-3 kg.s-1, the model is sensitive to HTF mass flow rate/heat transfer coefficient wall - HTF.
In general, the comparison of both theoretical and experimental results is satisfactory. The maximum RMS error in Figure 7 is 1.33 K for case TTF = 333 K, and 3.7 K for case TT,0 = 348K in Figure 8.
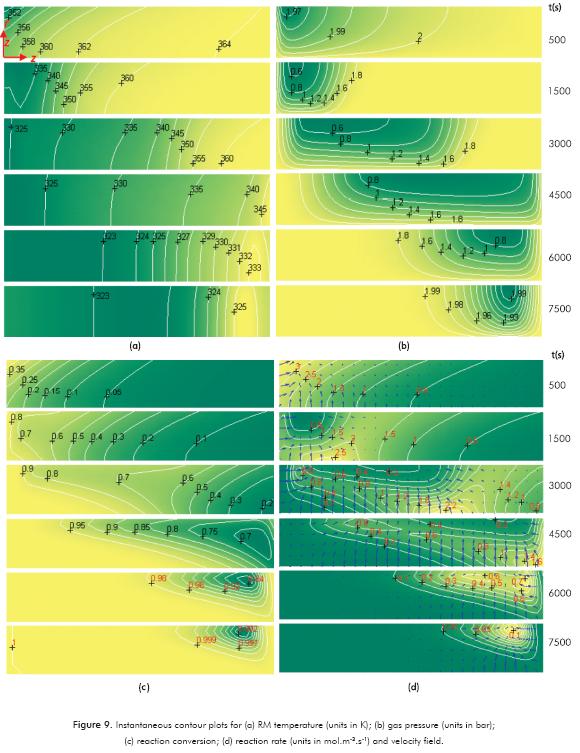
In order to have a general view of the reactor, instantaneous contour plots are presented in Figure 9 at different times for selected variables of the RM. In the contour plots, the reactor wall is located at the top boundary and the gas distributor is at the bottom. The coordinate system is only shown in the first contour plot of Figure 9a.
Mass transfer limitations can be observed in Figure 9b where pressure decays to 0.6 bar in zones near to the wall due to the gas reacting with the salt. In these areas, the reaction rate decreases because pressure is close to the equilibrium value at Ts. This “vacuum wave” is propagated in an axial direction as the reaction proceeds. In Figures 9a and c, temperature gradients in the radial direction are higher when heat transport is the controlling mechanism. Local minimums in the reaction conversion are observed in Figure 9c, where both mass and energy transport limitations are taking place. A reactive front close to the heat exchanger and another close to the gas distributor are taking place (see Figure 9d).
Simulation of a Single Effect Cycle
In order to analyze the model performance, a single effect cycle was simulated where the evaporator and cooling space models were linked to the reactor model. The dynamics of the condenser were neglected, and a constant condensation pressure was used for the decomposition step. The evaporator geometry is an annular cylinder with an inside diameter of 25 cm and an outside diameter of 26 cm, H = 25 cm. The following operational conditions were used:
- HTF mass flow rate: 5.6×10-3 kg.s-1.
- Inlet HTF temperature: 298 K for the synthesis and 460 K for decomposition steps.
- Initial temperature and pressure of the reactor at the synthesis step: 298 K and 2 bar, respectively.
- Water mass: 1.1 kg.
- Condensation temperature: 301 K.
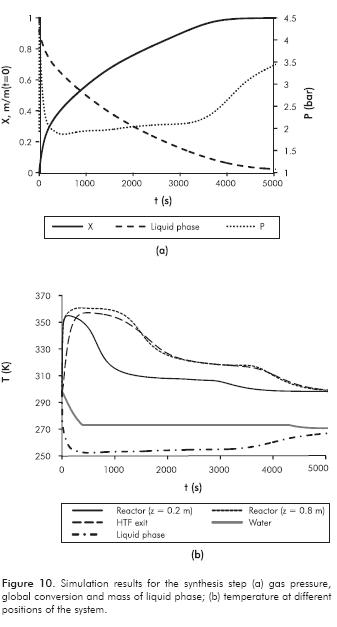
Simulation results for the synthesis step are presented in Figure 10.
At the onset of the synthesis step, it is observed in Figure 10a that pressure suddenly increases to 4.4 bar. The system evolves trying to reach the gas-liquid equilibrium state, evaporating the liquid refrigerant in part. Simultaneously, the gas is being transported towards the reactor and consumed there due to the chemical reaction.
This initial high pressure causes an increment in reaction rate as can be observed in Figures 10a and 10b where a stiff change is observed. Approximately 9.5% of the liquid phase is evaporated when the step starts and temperature drops to a minimum value. The liquid saturation pressure is close to the gas pressure and according to Equation 10, the evaporation rate decreases. After that, pressure decreases to a minimum value because the gas is being consumed in the reactor at a higher rate. However, in a real refrigerator, this effect would be lessened because of pressure drops in the system. Differences in reaction and evaporation rates yield non-constant gas pressure evolution. Qualitatively, the pressure behavior is similar to that observed in experimental results of Lahmidi et al. (2006) and Mauran et al. (2008) for SrBr2- H2O working pair and Li, Wang, Wang and Lu (2008) for CaCl2/activated carbon + NH3 working pair.
The temperature in the reactor (see Figure 10b) rises because the exothermic reaction is taking place. Simultaneously, reaction heat is transferred to the HTF in order to keep the reaction away from the equilibrium state. The maximum temperature suggests that heat transfer is the controlling mechanism; following this maximum, there is a slow variation in temperature, where mass transport is the controlling rate. The system evolves until the synthesis reaction has been completed. At the finishing period (t >3500 s), reaction rate is very low (controlling the chemical kinetics) and then reactor temperature gradually moves toward inlet HTF temperature. Simultaneously, pressure increases (in Figure 10a) because evaporation is still proceeding at a higher rate.
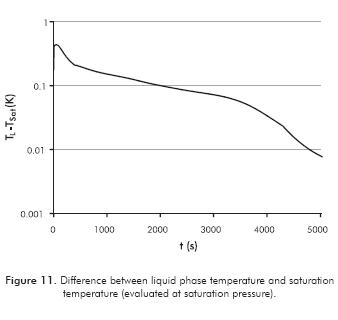
When evaporation takes place, the liquid temperature must be in accordance with saturation at gas pressure. The difference between these temperatures is shown in Figure 11, where little variation is observed. This difference can be understood as an excess of energy in the liquid phase in order for the evaporation to take place.
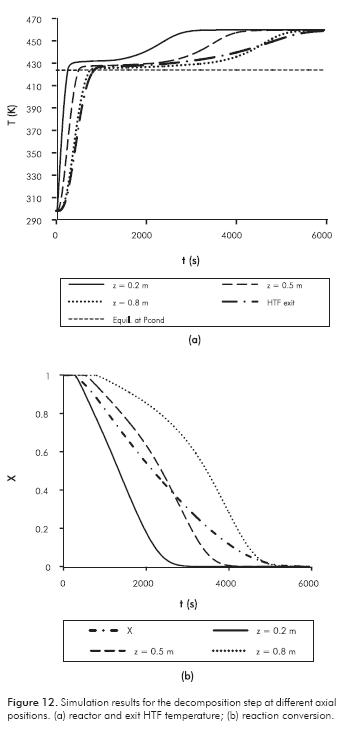
The simulation results for the decomposition step are presented in Figure 12.
In Figure 12a the RM temperature increases until it is greater than the equilibrium, and then endothermic decomposition reaction starts as observed in Figure 12b. At this point, the conversion is constant for the heating period. Like the synthesis reaction, Figure 12a shows that the temperature difference between the point and the equilibrium is greater for z = 0.2 than the other axial positions, and the duration of the chemical reaction is shorter. Most of the time the temperature is close to the equilibrium point, even when RM permeability is very low. In Figure 12b, the reaction rate is approximately constant for z = 0.2, and it decreases from t = 2200 (x = 0.1). Heat transfer is the controlling mechanism.
Coefficient of Performance (COP) is calculated in order to evaluate the thermodynamic cycle. For this system, COP takes into account the energy removed from the water during the synthesis step and the energy supplied to the RM during decomposition step:
The evaluation of Equation 24 for the system evaluated in this work is 0.219, which is within the range for practical single effect thermochemical cycles (0.15 - 0.30) (Goetz, 2000). Therefore, the COP calculated by the model presented in this work is in line with the observed experimental values for single effect configurations. In order to evaluate the impact of the evaporator model on the COP, the dynamics of the evaporator and cooling space were neglected by assuming an evaporator pressure of 2 bar. The COP for this scenario is 0.289, suggesting that the constant pressure assumption ove-restimated the COP by 32%.
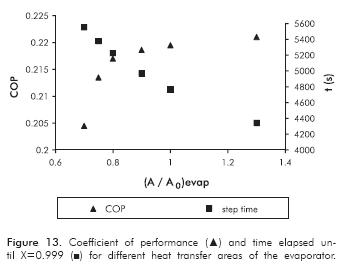
The impact of the evaporator heat transfer area on the cycle performance is presented in Figure 13. The evaporator heat transfer has been normalized with the area used for the simulation of the synthesis step in Figures 10 and 11.
Simulation results in Figure 13 show that the evaporator area has a non-linear effect on the cycle, being more sensitive on the COP than the synthesis step duration. For (A/A0) evap < 0.8 a faster change on the COP is observed. Refrigerant temperature and evaporation rate were lower than the other cases (results not shown here). A high temperature gradient with the environment takes place in longer times and, consequently, more cooling power is lost due to energy intakes. For these points, the liquid water did not completely solidify. Because of the low gas pressure, mass transfer limitations are more severe and then chemical reaction is expected to take more time.
4. CONCLUSIONS
- An unsteady, two-dimension mathematical model was developed for simulating the behavior of refrigerator based on a reversible chemical reaction. The model considers heterogeneous reactions between a solid bed and a gas phase during synthesis and decomposition steps. The texture changes and anisotropy of the reactive media were also accounted for. A global model for the evaporation process was proposed and coupled to the reactor model, in order to evaluate the dynamics of gas pressure and evaporation/reaction rates on the synthesis step. In addition, a water freezing process was coupled to the models. The set of partial differential equations were discretized following the finite volume method and the resulting non-linear equations were solved using the Gear method.
- The comparison of the simulation results and experimental data for a MnCl2+NH3 reactor showed that the model accurately reproduced the dynamics of the systems. Instantaneous temperature distributions in the reactor were used for validation as well as global conversion and HTF exit temperature, where good accuracy between model predictions and experimental observation was achieved. The maximum RMS deviation between simulation results and experimental data was 3.7 K. It is noted that the HTF flow rate has a higher impact on the simulation results suggesting that the HTF - wall heat transfer coefficient is a sensitive parameter that should be calculated in detail.
- Simulations revealed different rate-controlling mechanisms in the reactor for the synthesis and decomposition steps. Heat transfer as a controlling mechanism played an important role in both steps, but mass transfer was more important in the synthesis step. Chemical kinetics was of greater importance at the end of each stage. The two reactive fronts were identified from the two - dimensional plots.
- Differences between evaporation and reaction rates were obtained in the simulations when the evaporator and the cooling space models were considered. Pressure was not constant during the synthesis step simulation, as can be observed in similar experimental configurations. Pressure plays an important role in different phenomena taking place in the system, such as chemical kinetics, mass transfer and transport in the RM, evaporation temperature, heat transfer rate between evaporator and surroundings (cooling space), and duration of the evaporation step, among others.
- The model proposed in this work considers in a more approximated approach the dynamics of the refrigeration process including the non-linear behavior of the evaporator, as well as its interaction with the surroundings. It presents the COP calculated by our model as being in close agreement with those obtained in experimental devices. The model can be used for designing, evaluating and optimizing gas-solid refrigeration and heat pump systems as well as gas-solid reactors. Because the model has phenomenological basis, it can also be used for defining optimal control strategies of gas-solid refrigeration systems.
ACKNOWLEDGEMENTS
The authors thank Universidad Nacional de Colombia for logistic and financial support.
REFERENCES
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. (2002). Transport Phenomena, (2nd ed.), New York: John Wiley & Sons. [ Links ]
Castets, K. & Mazet, N. (2000). Analysis and optimization of the cyclic working mode of thermochemical transformers. Appl. Therm. Eng., 20(17), 1649-1666. [ Links ]
Cortés, F. B., Chejne, F., Mejía, J. M. & Londoño, C. (2009). Mathematical model of the sorption phenomenon of methanol in actived coal. Energy Convers. Manage. 50(5), 1295-1303. [ Links ]
Dutour, S., Mazet, N., Joly, J. L. & Platel, V. (2005). Mode-ling of heat and mass transfer coupling with gas-solid reaction in a sorption heat pump cooled by a two-phase closed thermosyphon. Chem. Eng. Sci., 60(15), 4093-4104. [ Links ]
Goetz, V. & Llobet, J. (2000). Testing and modeling of a temperature front solid-gas reactor applied to thermochemical transformer. Appl. Therm. Eng., 20(2), 155-177. [ Links ]
Gong, L. X., Wang, R. Z., Xia, Z. Z. & Chen, C. J. (2011). Design and performance prediction of a new generation adsorption chiller using composite adsorbent. Energy Convers. Manage., 52(6), 2345-2350. [ Links ]
Hoyos, J., Velásquez, J., Hill, A., Chejne, F. & Cháves, C. A. (2006). Principios termodinámicos de la refrigeración magnética. Dyna, 149: 95-105. [ Links ]
Jolly, P. & Mazet, N. (1999). Optimisation de la diffusion du gaz dans des matériaux réactifs, siège de transferts de chaleur, de masse et d'une réaction chimique. Int. J. Heat Mass Transf., 42(2), 303-321. [ Links ]
Kasta, W. & Hohenthanner, C. R. (2000). Mass transfer within the gas-phase of porous media. Int. J. Heat Mass Transf., 43(5), 807-823. [ Links ]
Lahmidi, H., Mauran, S. & Goetz, V. (2006). Definition, test and simulation of a thermochemical storage process adapted to solar thermal systems. Sol. Energy, 80(7), 883-893. [ Links ]
Le Pierrés, N., Mazet, N. & Stitou, D. (2007). Modeling and performances of a deep-freezing process using low-grade solar heat. Energy, 32(2), 154-164. [ Links ]
Le Pierrés, N., Stitou, D. & Mazet, N. (2008). Design of a thermochemical process for deep freezing using solar low-grade heat. Chem. Eng. Process, 47(3), 484-489. [ Links ]
Li, T. X., Wang, R. Z., Kiplagat, J. K., Chen, H. & Wang, L. W. (2011). A new target-oriented methodology of decreasing the regeneration temperature of solid-gas thermochemical sorption refrigeration system drive by low-grade thermal energy. Int. J. Heat Mass Transf., 54(21-22), 4719-4729. [ Links ]
Li, T. X., Wang, R. Z., Wang, L. W. & Lu, Z. S. (2008) Experimental study on an innovative multifunction heat pipe type heat recovery two-stage sorption refrigeration system. Energy Convers. Manage., 49(10), 2505-2512. [ Links ]
Lu, H. B. & Mazet, M. (1999). Mass-transfer parameters in gas- solid reactive media to identify permeability of IMPEX. AICHE J., 45(11), 2444-2453. [ Links ]
Mauran, S., Lahmidi, H. & Goetz, V. (2008). Solar heating and cooling by a thermochemical process. First experiments of a prototype storing 60 kW h by a solid/gas reaction. Sol. Energy, 82 (7), 623-636. [ Links ]
Mauran, S., Rigaud, L. & Coudevylle, O. (2001). Application of the Carman-Kozeny correlation to a high-porosity and anisotropic consolidated medium: the compressed expanded natural graphite, Transport Porous Med., 43(2), 355-376. [ Links ]
Mazet, N. & Lu, H. B. (1998). Improving the performance of the reactor under unfavourable operating conditions of low pressure. Appl. Therm. Eng., 18(9-10), 819-835. [ Links ]
Olives, R. & Mauran, S. (2001). A highly conductive porous medium for solid-gas reactions: effect of the dispersed phase on the thermal tortuosity. Transport Porous Med., 43(2), 377-394. [ Links ]
Parson, R. (2001). ASHRAE Handbook: (SI Edition, rev Edition). Atlanta: ASHRAE. [ Links ]
Patel, N. & Teja, A. (1982). A new cubic equation of state for fluids and fluid mixtures, Chem. Eng. Sci., 37(3), 463-473. [ Links ]
Pons, M., Laurent, D. & Meunier, F. (1996). Experimental temperature fronts for adsorptive heat pump applications. Appl. Therm. Eng., 16(5), 395-404. [ Links ]
Saha, B. B, Chakraborty, A., Koyama, S. & Aristov, Y. I. (2009). A new generation cooling device employing CaCl2-in-silica gel-water system. Int. J. Heat Mass Transf., 52(1-2), 516-524. [ Links ]
Stitou, D. & Crozat, G. (1997). Dimensioning nomograms for the design of fixed-bed solid-gas thermochemical reactors with various geometrical configurations. Chem. Eng. Process, 36(1), 45-58. [ Links ]
Velásquez, J. E. & Chejne, F. (2004). Fenómenos de transporte y transferencia, (1st ed.), Medellín: Universidad Nacional de Colombia, sede Medellín, Centro de Publicaciones. [ Links ]
Verteeg, H. K. & Malalasekera, W. (1995). An introduction to computational fluid dynamics, the finite volume method. 1st ed., New York: Longman Scientific & Technical. [ Links ]
Wang, D. C., Xia, Z. Z., Wu, J. Y., Wang, R. Z., Zhai, H. & Dou, W. D. (2005). Study of a novel silica gel-water adsorption chiller. Part I. Design and performance prediction. Int.J. Refrig., 28(7), 1073-1083. [ Links ]
Wu, W. D., Zhang, H. & Sun, D. W. (2009). Mathematical simulation and experimental study of a modified zeolite 13X-water adsorption refrigeration module. Appl. Therm. Eng., 29(4), 645-651. [ Links ]
Zhao, Y. L., Hu, E. & Blazewicz, A. (2012). A non-uniform pressure and transient boundary condition based dynamic modeling of the adsorption process of an adsorption refrigeration tube. Appl. Energ., 90(1), 280-287. [ Links ]
Ziegler, F. (1999). Recent developments and future prospects of sorption heat pump systems. Int. J. Thermal Sci. 38(3), 91-208. [ Links ]